机器人关节摩擦建模与自适应RBF神经网络补偿计算力矩控制

沈晓斌，王斌锐，余 芮，崔小红

(中国计量大学 机电工程学院，浙江 杭州 310018)

机器人关节是组成机械臂的最小组成单元，通常由电机、减速器、传感器和驱动器组成。由于谐波减速器体积小、质量小、传动比大、负载能力强，故机器人关节多采用谐波减速器。但谐波减速器、轴承等器件中存在非线性摩擦[1]，使关节动力学模型复杂，控制困难、效果不佳。

对于关节处存在的非线性摩擦，研究者们提出了许多摩擦模型，主要分为动态摩擦模型和静态摩擦模型。动态摩擦模型能准确描述关节处存在的摩擦力，较常用的模型为LuGre模型。TAN等[2]使用LuGre模型为机械系统进行摩擦建模，贺莹等[3]为单关节伺服系统以LuGre模型进行建模，但从建模过程可见实际测量难度较大，建模过程复杂，不利于实际工程应用。在实际工程中较多使用静态模型。静态摩擦模型[4]包括库伦摩擦模型、粘滞摩擦+库伦摩擦模型、静摩擦+粘滞摩擦+库伦摩擦模型、Stribeck模型等。其中Stribeck模型能较精确描述静态摩擦特性，较为常用。付建宁[5]等人在机器人关节建模时加入Stribeck摩擦模型，利用前馈进行摩擦补偿，提高关节控制精度，但存在建模不准确的问题，并且机器人关节处的摩擦特性还会受到其他许多因素的影响。如NEVMERZHITSKIY[6]、吴晓敏[7]等认为摩擦特性应与温度有关，需建立与温度相关的摩擦模型；LIAO[8]、HAN[9]等认为摩擦特性还应与位置相关，需建立与位置相关的摩擦模型。与温度和位置相关的摩擦模型建模复杂、实现困难，且无法消除建模误差。因此，本文考虑对摩擦模型的建模误差进行在线观测和辨识，以实现更精确的补偿。

在机器人关节轨迹跟踪控制方法中，常用的方法有PID(Proportional Integral Derivative)控制法、反馈线性化控制法、计算力矩控制法[10]以及与模糊控制、神经网络[11-12]等先进控制算法结合的控制方法。如WANG等[13]在具有Stribeck摩擦建模的机器人系统中使用模糊PID控制，但模糊控制依赖于使用者的经验；CAMBERA等[14]使用反馈线性化控制法进行柔性关节控制，但反馈线性化控制需系统的状态量可观测。计算力矩控制法基于系统的动力学模型[15]，算法简单实用，可应用于实际机器人关节系统。但由于实际系统的精确动力学模型很难得到，尤其是必须考虑非线性摩擦对系统的影响，因此JIANG等[16]在计算力矩控制的基础上，加入自适应RBF神经网络(Radial Basis Function径向基)对未建模动态进行在线补偿。但由于低速运行时尤其是关节电机启停时，摩擦力出现较强的非线性，此时RBF不能很好地补偿非线性摩擦。

在上述研究背景下，本文将在对非线性摩擦建模基础上，设计自适应RBF神经网络对摩擦模型误差和动力学模型参数误差等未建模动态进行在线观测，设计含摩擦模型的自适应RBF神经网络补偿计算力矩控制器。进行摩擦建模可降低模型的非线性程度，降低控制难度；自适应RBF神经网络结构简单且具有逼近任意非线性函数的能力，结合权值自适应律，能对摩擦模型误差和动力学模型参数误差进行有效在线逼近和观测；计算力矩控制法具有算法简单直观、鲁棒性好等特点，并且容易应用于实际系统。因此，将三者集成可提高关节控制精度。

本文首先基于Stribeck摩擦模型和拉格朗日方程，对机器人关节建立动力学模型，并在模型中加入未建模动态，提高模型的准确性；其次，通过实验测量及最小二次法对摩擦模型参数进行辨识；然后，利用自适应RBF神经网络对摩擦建模误差和动力学模型参数误差进行在线观测，并补偿到计算力矩控制器中；最后，在自主设计的关节和测试平台上，对所设计的控制器进行了测试。

1 机器人关节动力学模型

1.1 关节建模

本文以自主设计的无刷直流伺服电机和谐波减速器构成的单自由度机器人关节为研究对象，机器人关节三维样机模型如图1。

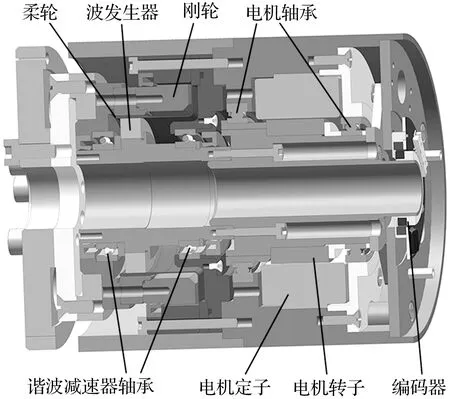
图1 机器人关节样机模型Figure 1 Prototype model of robot joint

将减速器按速度大小分为高速侧和低速输侧，电机轴为高速轴，谐波减速器输出侧轴为低速轴。通过分析，可得关节传动链机构简图如图2。

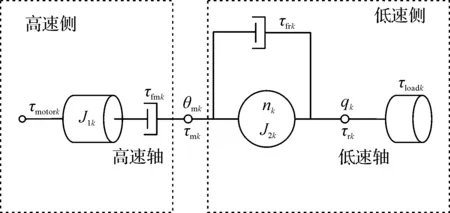
图2 关节传动机构简图Figure 2 Diagram of joint transmission mechanism

图2中τmotor表示电机产生的电磁力矩，Nm；J1表示高速轴的转动惯量，kg·m2；τfm为高速端摩擦力矩，Nm；θm为高速端转角，rad；τm为高速端输出到力矩，低速端输入力矩，Nm；τfr为低速端摩擦力矩，Nm；n表示减速比；J2表示低速轴转动惯量，kg·m2；q表示低速端转角，rad；τr表示低速端输出力矩，即负载力矩τload，Nm。

直流伺服电机产生的电磁力矩与电流成正比：

τmotor=Kmi。

(1)

式(1)中：Km为电机力矩常数，Nm/A；i为电机电流，A。

通过分别对高速轴和低速轴建模，可得机器人关节的动力学模型。

首先进行高速轴建模。由输入和输出力矩平衡原理以及图2所示机构简图，可得高速轴动力学方程为

(2)

然后进行低速轴建模。同理可得低速轴动力学方程为

(3)

基于拉格朗日方程，负载τr可以表示为

(4)

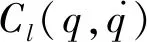
假设谐波减速器刚度足够大，忽略谐波减速器的变形，可得到高速轴转角θm和低速轴转角q的关系为

q=θm/n。

(5)

由式(1)到式(4)可得机器人关节的动力学模型为

(6)

其中J=n2J1+J2表示等效转动惯量，kg·m2；τf=τfm+τfr/n表示高速端的等效摩擦力矩，kg·m2。

1.2 关节非线性摩擦建模

速度对摩擦的影响最大，因此本文在建立摩擦模型时只考虑与速度相关的摩擦力矩模型，忽略温度、位置等其他因素对建模的影响。基于静态摩擦模型中的Stribeck模型，关节摩擦力矩可表示为：

(7)

由式(1)和式(6)可得关节摩擦力矩τf与电机电流i的方程

(8)

当机器人关节处在空载且匀速运动状态下，电机产生的电磁力矩和摩擦力矩相等，可得

τf=Kmi。

(9)

由式(9)可计算得到高速端的等效摩擦力矩τf，τf中包含了τfm和τfr。

1.3 摩擦力模型参数辨识

为了辨识摩擦模型的参数，在自主研制的机器人关节上开展参数辨识实验。关节传动系统主要由无刷伺服电机和谐波减速器组成，电机轴和减速器输入轴直接相连。同时，在关节的一侧装有旋转编码器，对关节的转动角度进行测量。电机选用Kollmorgen的直流无框电机TBM7615A，谐波减速器选用苏州绿的的LHSG-20-CL-120，编码器选用北京金钢科技的MBS磁编码器，驱动器使用Elmo的G-MOLWHI20/100SE。机器人关节的主要性能参数如表1。

表1 机器人关节主要性能参数Table 1 Main performance parameters of robot joint

实验方法：将机器人关节设置于空载状态，记录不同速度下电机的输出力矩。速度取值范围为[-62.4,62.4] rad/s，其中当速度大小范围为(0,5.2) rad/s时步长为0.52 rad/s、[5.2,52) rad/s时步长为1.04 rad/s、[52,62.4] rad/s时步长为5.2 rad/s。

在MATLAB中，利用实验测所得数据，使用最小二乘法对正反两个方向的摩擦模型参数进行辨识。最终拟合的角速度-摩擦力矩拟合曲线如图3，辨识得到的参数如表2。

表2 摩擦模型参数辨识结果Table 2 Parameter identification results of friction model

由图3可见，使用摩擦模型对关节处的摩擦特性进行建模仍具有一定的误差，不能精确的描述。所以有必要对建模误差进行在线辨识和补偿。

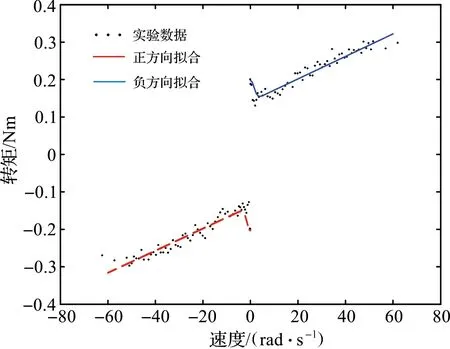
图3 速度-摩擦力矩拟合图Figure 3 Velocity-friction torque fitting diagram

2 控制器设计

2.1 自适应RBF神经网络补偿计算力矩控制器设计

本文采用计算力矩控制法，对含非线性摩擦力的机器人关节进行轨迹跟踪控制器设计。同时，结合自适应RBF神经网络对摩擦模型误差和动力学模型参数误差进行在线观测和补偿。自适应RBF神经网络补偿计算力矩控制的系统框图如图4。

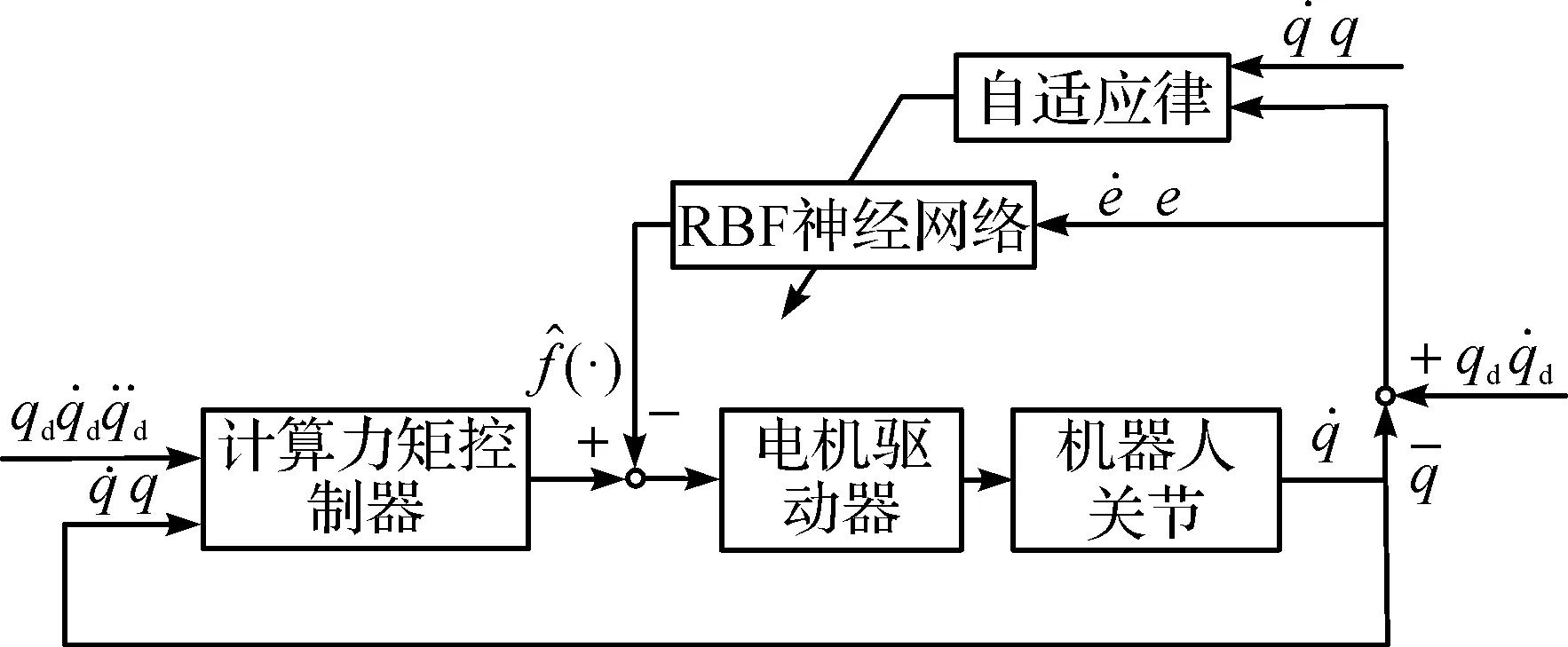
图4 控制系统框图Figure 4 Control system block diagram

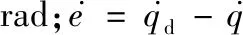
(10)

综合考虑公式(10)中摩擦模型误差和动力学模型参数误差等未建模动态，设含未建模动态的机器人关节动力学模型为

(11)

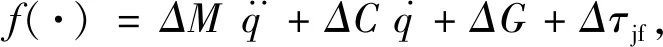
M(q)=M0(q)-ΔM，

G(q)=G0(q)-ΔG，

τjf=τjf0-Δτjf。

由式(11)给出的动力学模型采用计算力矩控制法，可设计控制律如下：

(12)

假设f(·)已知时，结合式(10)和式(12)，可得到系统误差方程为

(13)

式(13)中，kv为速度反馈增益系数；kp为位置反馈增益系数。选择合理的kv、kp即可使系统的闭环极点具有负实部，保证控制系统的稳定性。

实际工程中f(·)往往是未知的，因此本文采用自适应RBF神经网络方法进行在线估计和补偿。

2.2 自适应RBF神经网络摩擦模型误差补偿

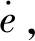
采用的径向基函数为高斯核函数

(14)

式(14)中，x为输入向量；bi为第i个高斯径向基函数宽度；ci为第i个神经元高斯径向基函数的中心向量。

RBF神经网络逼近的f(·)可表示为

(15)

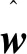
由式(12)和式(15)，可得本文所设计的自适应RBF神经网络补偿计算力矩控制器控制律为

(16)

设计自适应律为

(17)

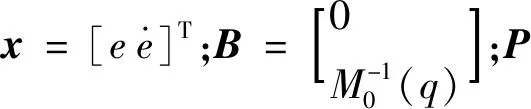
PA+ATP=-Q。

(18)

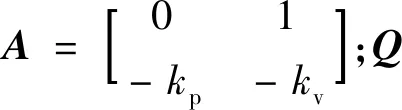
公式(18)给出了保证控制算法稳定的控制参数约束条件。

3 实验分析

为了验证方法的有效性，本文在自主研发的单自由度机器人关节上进行实验验证。实验装置如图5所示。其中控制器用于产生轨迹、接收反馈信号以及发送控制指令，计算机用于记录实时轨迹、控制量等日志数据。

图5 实验装置图Figure 5 Experimental device diagram

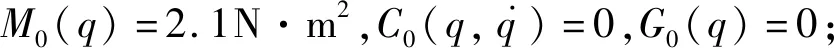
b=[5 5 5 5 5 5 5 5 5 5 5 5 5 5 5]。

中心向量为

其中，中心向量和基函数宽度的值是通过只含有计算力矩控制时的跟踪误差范围以及实际实验调试效果确定的，因此这也是该方法的不足之处。

由于正反两个方向摩擦模型参数数值相差较小，为了简化实验模型，将对应摩擦模型参数求平均值后可得摩擦模型为

本文实验主要涉及含摩擦模型的自适应RBF神经网络补偿计算力矩控制、无摩擦模型的自适应RBF神经网络补偿计算力矩控制、传统计算力矩络控制这三种控制方法的轨迹跟踪实验，图6和图7为关节输出端跟踪轨迹图和误差图，图8和图9为关节输出端的神经网络等效输出。表3列出了系统在运行200 s后角度误差范围对比。

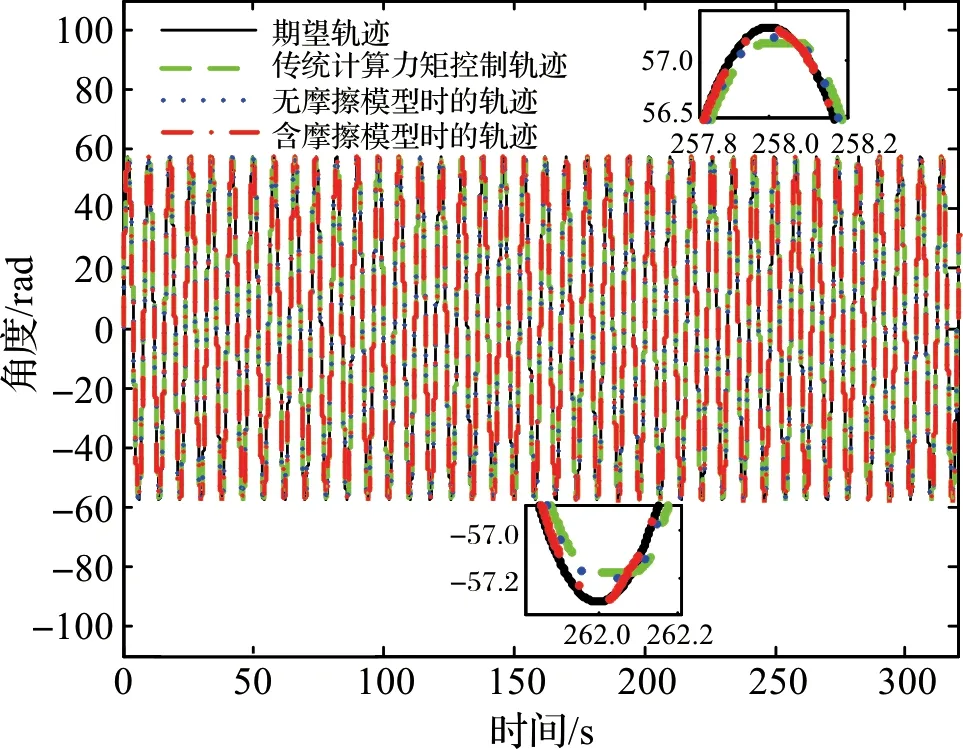
图6 轨迹跟踪图Figure 6 Trajectory tracking curves

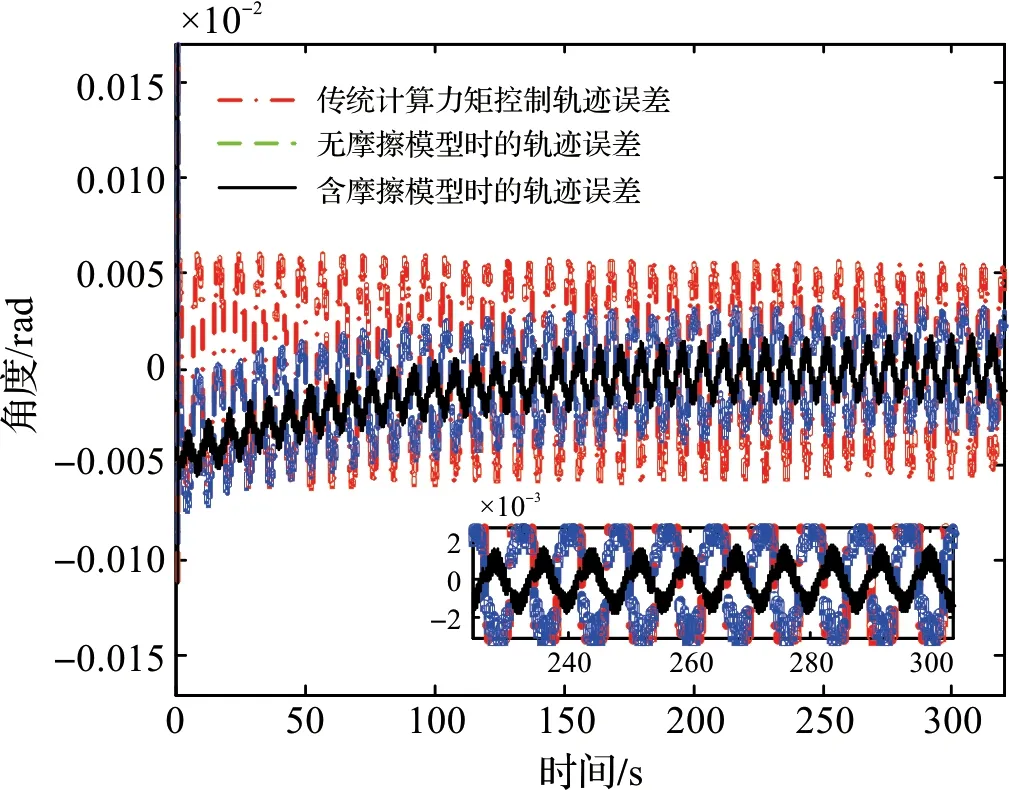
图7 角度轨迹误差对比图Figure 7 Comparison of angle tracking error curves

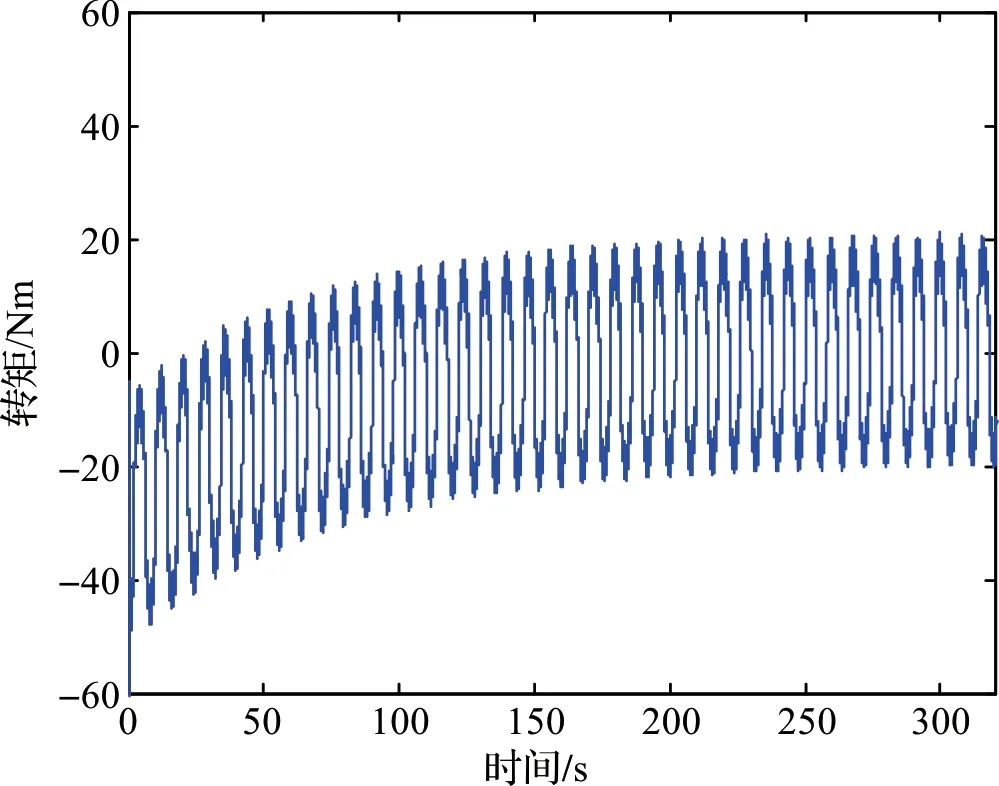
图8 无摩擦建模时神经网络输出Figure 8 Neural network output without friction modeling

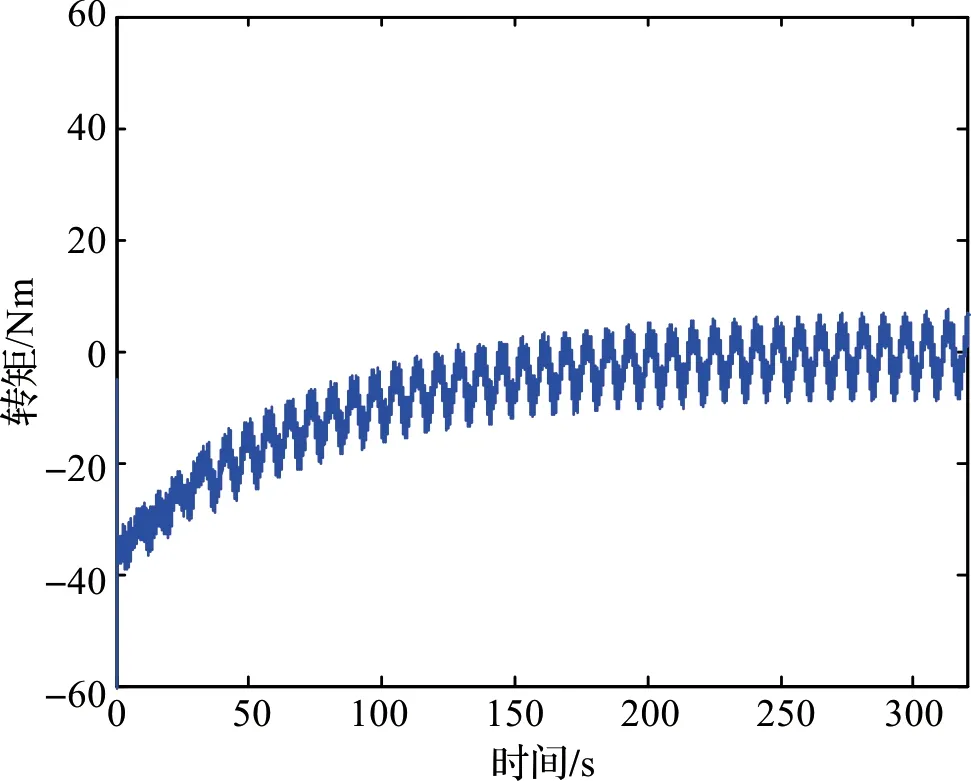
图9 含摩擦建模时神经网络输出Figure 9 Neural network output with friction modeling

表3 角度轨迹跟踪误差对比Table 3 Comparison of angle tracking errors

图6是传统计算力矩控制、无摩擦模型的自适应RBF神经网络控制、含摩擦模型的自适应RBF神经网络控制轨迹跟踪对比图，图7是三种控制方式的角度轨迹跟踪误差对比图。从图6的局部放大图中可以看出在到达轨迹最值即速度为零时误差较大，该部分的误差主要是由于关节处存在摩擦引起的，在控制器输出的控制力矩小于关节静摩擦力时，关节输出轴将处于静止状态，导致无法跟踪理想信号。传统计算力矩控制和无摩擦模型的自适应RBF神经网络控制这两种控制方法误差较为明显。虽然在传统计算力矩控制器的基础上加入自适应RBF神经网络补偿后，可以从图7误差对比图中看出，当达到稳定时自适应RBF神经网络补偿计算力矩控制器的误差明显减小，但是由于神经网络的学习能力有限，仍然没有能够很好的补偿关节处存在的非线性摩擦。经过关节摩擦建模后，由图6中的局部放大图可以看出，当进行摩擦建模并补偿时的响应速度更快，摩擦带来的影响大大减小。由图7给出的跟踪误差对比也可以看出，在达到稳定时跟踪误差明显降低。

在200 s后跟踪误差基本趋于稳定，由表3列出的轨迹跟踪误差范围可得，含摩擦模型的自适应RBF神经网络补偿计算力矩控制追踪误差±1.83×10-3rad是无摩擦模型控制追踪误差±3.32×10-3rad的55.12%，是传统计算力矩控制追踪误差±5.85×10-3rad的31.28%。

图7可以看出，在加入自适应RBF神经网络补偿后，需要经过200 s轨迹跟踪误差趋于稳定状态。引起该现象的主要原因是由于神经网络有一个学习的过程，经过一段时间后学习完成误差趋于稳定。200 s的收敛时间相对较长，但是如果每次关机时记录神经网络参数，则在下一次开机时并不需要重新学习，因此200 s的收敛时间只会在神经网络第一次学习时出现，并不影响后续使用过程中算法的性能。

4 结 论

本文基于拉格朗日方程和Stribeck模型对单自由度机器人关节进行动力学建模，并利用最小二乘法对摩擦模型参数进行辨识；基于含未建模动态的机器人关节动力学模型，设计了自适应RBF神经网络补偿计算力矩控制器，实现关节角度轨迹跟踪。理论分析和实验表明：

1)在动力学模型中，加入非线性摩擦模型，降低了系统输入输出的非线性，提高了自适应RBF神经网络对机器人关节动力学模型未建模动态的逼近能力；

2)选取合适的计算力矩参数以及李雅普诺夫方程中正定矩阵Q可以保证系统稳定与收敛性；

3)本文设计的控制算法轨迹跟踪精度优于传统计算力矩控制和无摩擦模型的自适应RBF神经网络补偿计算力矩控制。