基于像素偏振阵列的图像传感器航向角检测

陈智慧，金尚忠，王 赟，侯 彬，曹馨艺

(中国计量大学 光学与电子科技学院 浙江省现代计量测试技术及仪器重点实验室，浙江 杭州 310018)

太阳光经过大气层时会被大气中的分子散射，经散射后的光线会具有独特的偏振模式，从而在地表附近可以观察到具有规律性的偏振分布信息[1]。研究表明自然界中有许多昆虫具有特殊的生物器官能够感知大气中的偏振信息[2-3]，并且能够根据这些偏振信息进行定位和导航。南非草原上的蜣螂在出发觅食前会旋转自己的身躯分辨天空中的偏振模式以保持正确的觅食方向[4]。沙蚁、金斑蝶等昆虫同样具有相同的导航能力[5]。

根据昆虫的导航机理，国内外的科研人员设计研发了许多仿生偏振导航传感器[6]。褚金奎团队[7]在2009年设计的六通道光电式偏振传感器在标定后的导航精度达到了0.2°，在移动机器人距离为32 m的导航实验中估计轨迹的平均误差为42 cm。2012年Javaan Chahl和Akiko Mizutani[8]开发了两种检测环境光和偏振光分布的点源式仿生偏振传感器，安装在无人机上实现了维持稳定飞行和导航，开启了飞行器导航的新途径。2018年Julien Dupeyroux等[9]使用两个紫外光光电传感器组成导航传感器来确定太阳子午线方向角，结合光流传感器在晴朗天气条件下进行5 m导航实验，最终导航误差为4.8 cm。

然而，基于点源式的偏振导航传感器在不断变化的户外环境中极易受到干扰。因此，科研人员开始研究稳定性和鲁棒性更高的基于图像的偏振测量方法，根据偏振分布图中太阳子午线的方向辨别航向角。2014年中国科学技术大学的Daobin Wang等[10]设计了一款基于相机的三通道仿生偏振相机，采用傅里叶变换拟合传感器的特征曲线减少误差后，再采用线性插值缩小图像降低数据量，传感器的最大误差和平均误差分别为0.650 3°和0.325 6°。2015年国防科技大学的胡小平团队[11]使用4个CCD相机设计了一款4通道仿生偏振导航传感器，提出了一种基于最小二乘法的测量方法，在室外实验中发现偏振光导航的精度和天空光的偏振度相关，当偏振度大于0.15时传感器的测量误差小于0.9°，得到在傍晚时刻导航效果较好的结论。2018年清华大学韩勇[12]设计了一款旋转式偏振相机，利用电机旋转偏振片实现了快速偏振图像采集，该装置和前两种传感器相比结构尺寸有了一定程度的缩小，但无法达到实时的效果。同年褚金奎设计了阵列式偏振导航传感器，基于线性灰度拉伸的Otsu阈值分割和3σ法则实现了遮挡物干扰情况下的偏振光强提取[13]，定向精度为0.25°，解决了存在遮挡物时精准导航的问题。

基于图像的多通道偏振导航传感器相比于点源式传感器虽有稳定性高的优势，但是复杂的多个相机结构和较高的设备成本、重量体积势必会影响其应用价值。而基于单个相机的单通道传感器在测量时需要不断转动相机表面的偏振片，无法对偏振光进行实时检测而且还要防止振动。

为满足高稳定性、微型化、低成本等要求，本文使用了像素偏振阵列结构的芯片相机，搭建了偏振导航传感器。该传感器在测量时仅需要一个相机并且无需旋转偏振片，单次拍摄即可得到0，45°，90°和135°四幅偏振图像，具有集成度高和测量方便的优点。本文采用的是基于图像的航向角计算方法，针对初始偏振角度图片无对称性的问题，通过对偏振角度图进行坐标转换提取子午线方向，并且和基于特征向量的太阳矢量估计方法进行了导航精度对比，说明了本方案的可行性。

1 偏振导航传感器

1.1 传感器结构

本文使用的偏振导航传感器如图1所示，由1个500万像素CMOS传感器和1个镜头(焦距为25 mm，视场角D×H×V为23.5°×18.8°×14.2°)两部分组成，传感器整体大小为30 mm×30 mm×85 mm(长×宽×高)。

图1 偏振导航传感器Figure 1 Polarization navigation sensor

相机中CMOS芯片表面的偏振阵列的结构示意图如图2。像素偏振阵列由2 448×2 048个像素单元组成，单个像素单元的大小为3.45 μm×3.45 μm。阵列以4个像素单元为一组规律分布，每个像素单元上都有一个偏振方向固定的微偏振片，偏振角度分别为0°，45°，90°和135°，每个像素单元的偏振角度和与之相邻的8个像素单元都不相同。Kiyotaka Miura在2017年制备的石英玻璃像素偏振阵列[14]，在使用时是将石英玻璃阵列安置在芯片微透镜上。而本文使用的偏振阵列结构直接安置在每个CMOS面阵光电二极管像元的表面，再在偏振阵列上加微透镜，以避免检测到相邻像素上的偏振光导致的信息串扰。以偏振角度约为90°的偏振光照射微偏振阵列芯片，对拍摄的强度图局部放大可观察如图3所示均匀分布明暗不同的强度图像，在偏振方向相垂直的0°方向上最暗，在偏振方向相同的90°方向上最亮。

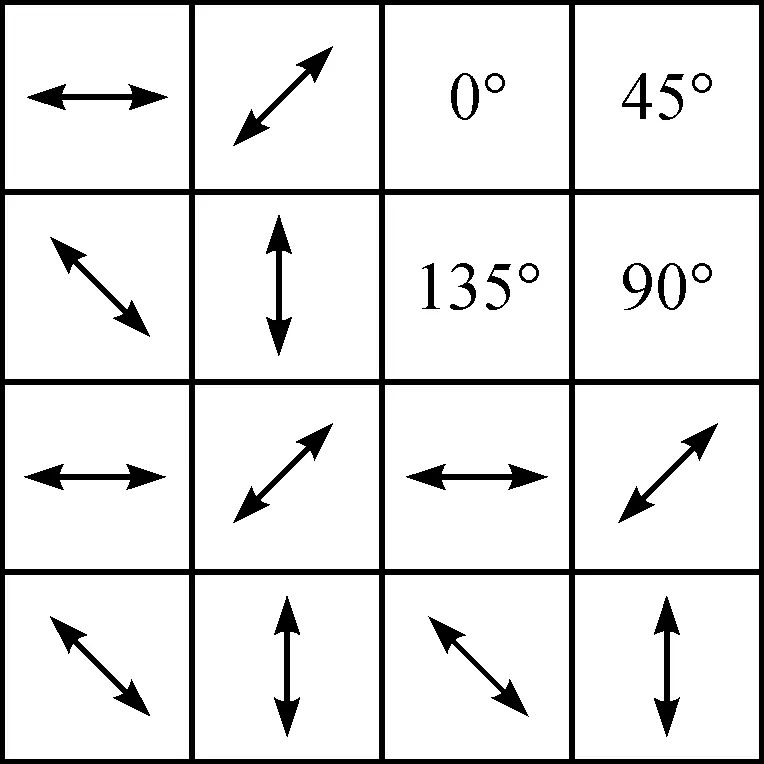
图2 像素偏振阵列结构示意图Figure 2 Pixel-level polarization array structure diagrammatic sketch

图3 约90°偏振光照射时拍摄的强度图片部分区域Figure 3 Part of the intensity image under the approximately 90° linearity polarized light

1.2 图像插值算法

该偏振导航传感器具有较高的集成度能在每一帧采集4种偏振信息，在偏振态计算过程中将相邻4个像素视作一个单位的计算方法会损失图片的空间分辨率。因此本文使用双线性插值算法和像素梯度插值算法将原始偏振图片转化为四幅偏振角分别为0°，45°，90°和135°的偏振图，以此保留其空间分辨率。

图4为利用双线性插值算法合成0°，45°，90°和135°四幅偏振图片的方法流程。从偏振原始图片中提取出所有偏振方向为0°的像素，得到如图4(a)所示的仅包含四分之一信息的0°偏振图。图中2×2区域空白处数据的双线性插值计算方法如下：

(1)

(2)

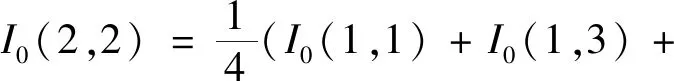
(3)

使用双线性插值对图4(a)中所有的空白位置进行双线性插值填补，最终得到的偏振图片示意图如图4(b)，保留有和原始图片相同的分辨率并包含完整的0°偏振信息。同理可插值填补得到45°，90°和135°的偏振图片。

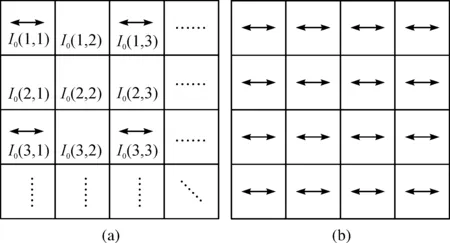
图4 双线性插值算法示意图Figure 4 Bilinear Interpolation Method schematic diagram

像素梯度插值算法是在双线性插值算法的基础上，对图片中梯度超过阈值的区域进行选择性卷积的算法。从原始图片拆分得到0°，45°，90°和135°4幅含空白区域的偏振图片，对4幅偏振图片中所有7×7相邻像素区域以述公式计算梯度：

(4)

其中，D0°为水平方向的梯度，D90°为垂直方向的梯度，D45°为45°方向的梯度，D135°为135°方向的梯度，i为像素横坐标，j为像素纵坐标。

图5(a)黑色区域为灰度已知像素，白色区域为待求像素，图片中心黑色圆点为插值计算的目标像素。目标像素的水平方向和垂直方向无已知像素，因此D0°和D90°为0。对其进行梯度运算，若该点满足D45°/D135°>1.2，则沿135°方向进行卷积插值；若该点满足D135°/D45°>1.2，则沿45°方向进行卷积插值；其余情况下，目标像素用双线性插值方法进行插值，完成初步插值。

从完成初步插值的图像中提取7×7像素区域得到图5(b)所示图片，对其进行梯度运算，若该点满足D0°/D90°>1.2，则沿90°方向进行卷积插值；若该点满足D90°/D0°>1.2，则沿0°方向进行卷积插值；其余情况下，目标像素用双线性插值方法计算，最终得到完整的偏振图片。

卷积过程如下表示：

I(x，y)=∑W(s)f(x+s，y)；

(5)

(6)

式(5)(6)中，I(x，y)为待插值像素，f(x，y)为已知像素，W(s)为卷积核，s为待插值点和已知像素点的距离。

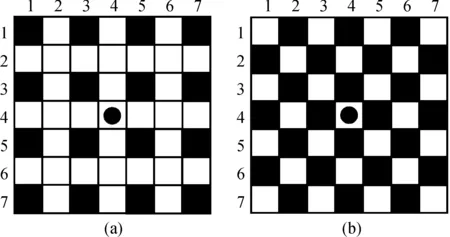
图5 基于梯度插值算法示意图Figure 5 Gradient based interpolation algorithm schematic diagram

和双线性插值算法相比像素梯度插值算法计算精度高，合成的高分辨率图片图像轮廓细节更为清晰明显，有利于提高图像中对象轮廓边缘区域的插值精度。使用像素梯度插值算法时，大量的数据计算导致处理器合成图片时间过长，在处理效率上远不及线性插值算法，无法满足实时性要求。由于偏振相机拍摄的是天空区域，图片颜色单一且无遮挡物干扰，像素间无明显的梯度变化，因此使用像素梯度插值算法解算得到的航向角在精度上没有明显优于双线性插值算法得到的精度。

在偏振导航应用中，首先需要保证导航的实时性，在此基础上逐步提升导航的精度。在像素梯度插值算法处理图片的效率无法显著提高的情况下，综合考虑导航精度和航向角计算的实时性，采用双线性插值算法合成4幅偏振图像。

1.3 偏振态解算

斯托克斯矢量可以用于定义包含线偏光、圆偏光、椭圆偏振光等形式入射光的偏振态，其具体形式如下：

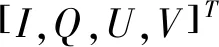
(7)

其中，I为入射光的总光强，Q和U表示入射光两个正交线偏振方向上的光强，V为入射光圆偏振方向的光强。

斯托克斯矢量可以通过3个或者3个以上偏振角度的光强联立求解，本文中使用的微偏振阵列中的偏振片角度有4个方向0°，45°，90°和135°，因此斯托克斯矢量可如下式计算：

(8)

其中，在自然条件下的圆偏振分量非常微小，因此通常将其忽略。

偏振度DOP表示为偏振光的光强在总光强中的占比，通常取值范围在0～1之间，DOP可以用斯托克斯矢量计算，偏振光线中的偏振角AOP也可通过斯托克斯矢量计算，结合公式(8)得到：

(9)

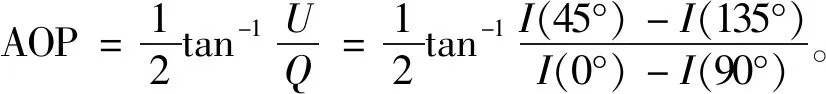
(10)

2 基于图像的航向角计算方法

将偏振相机正对天空拍摄一张偏振图片，由于本文所使用的偏振相机只能拍摄到灰度图，为便于观察使用伪彩方法将灰度图转换为彩色图。图6(a)即为偏振相机拍摄到的具有四个偏振方向的原始偏振图片，为了拍摄空间有个参照体，在拍摄时刻意使用偏振相机拍摄到一点房角作为参照。偏振图片中靠近太阳的位置亮度较高转换为彩色图时的颜色偏红，因此可以通过颜色从原始图片中判断出太阳方位。使用插值算法从原始图片中拆分并合成出原始图片相同分辨率的0°，45°，90°和135°四幅偏振图，图6中的(b)、(c)、(d)、(e)即为对应角度的偏振图片。受到大气粒子散射天空中存在部分偏振光，合成的4个偏振方向的偏振图片中的部分区域亮度有所不同，无法辨认子午线只能从中辨别太阳的大致方位。

使用公式(10)结合四幅不同偏振方向的偏振图可计算得到一幅偏振角图片，偏振角图片边缘区域的像素位置拍摄到干扰物存在一定的误差，因此以图片中心为原点半径为1 000个像素将偏振角图片裁剪成如图7(a)所示的圆形。偏振导航是以稳定的天空偏振模式作为导航基准，偏振角以子午线为对称轴呈“∞”型分布，子午线上偏振角为90°。而此时图7(a)中显示的偏振角为E矢量方向与相机参考坐标轴之间的夹角，偏振角分布在-35°～0°之间，和“∞”型图形不同，没有明显的规律和对称性，无法从中辨认出子午线的方向，不能直接用于太阳方位角直接求解。因此本文采用坐标系重绘[15]的方法并加以详细描述。

图6 原始偏振图片和4个偏振方向的偏振图片Figure 6 Original polarization picture and polarization pictures in 4 polarization directions

图7 偏振角图Figure 7 Angle of polarization

如图8所示以偏振阵列芯片平面中心点为原点O，芯片长宽方向为x和y轴建立xoy相机坐标系。将三维天球坐标系投影到相机坐标系表面，S为太阳在坐标系平面投影的点，太阳和原点相连的直线为投影的太阳子午线。以投影的太阳子午线和子午线垂直方向为s和t轴建立sot子午线坐标系，此时可以将太阳看作为高度角为0°时的理想状态。

M为观测点，OM为观测方向，N是M以子午线s为对称轴的对称点。在天空偏振模式中天空任意位置的偏振光偏振方向垂直于该点与太阳之间的连线，因此观测点M和N上偏振光的偏振方向为LM和LN的垂线方向LM和LN。定义x轴方向为偏振0°方向，则M和N点的偏振角分别为θ1和θ2。明显的，θ1和θ2大小不等，因此在相机坐标系中以子午线为对称轴的观测点没有明显的关联性。在相机坐标系中以x轴方向为偏振0°方向所作的偏振分布图如同图7(a)，无法从图片中辨别子午线方向。

以子午线坐标系为参考系s方向为偏振0°方向时，M和N点的偏振角为∠SLM和∠SLN，两个偏振角绝对值大小相等且对称轴为子午线，具有较强的对称性。但偏振图中的子午线方向会随着相机转动而改变且是未知的，无法直接求解∠SLM和∠SLN。但是在子午线坐标系中M点和N点两个观测点上存在两个以子午线为对称轴对称的角φ1和φ2，φ1、φ2绝对值大小相等，并且和θ1、θ2互为内角关系，根据几何理论φ1和φ2可由下式计算得到：

(11)

其中，∠MOK和∠NOK是M点和N点的方位角可直接由像素坐标计算；θ1和θ2为M点和N点在相机坐标系上的偏振角。

根据式(5)将偏振图7(a)中所有的偏振角重绘后得到的偏振图像如图7(b)，该图偏振角分布均匀，具有极为的对称性明显，由偏振角度为90°的点组成的子午线可清晰辨认，适用于后续太阳方位角计算。

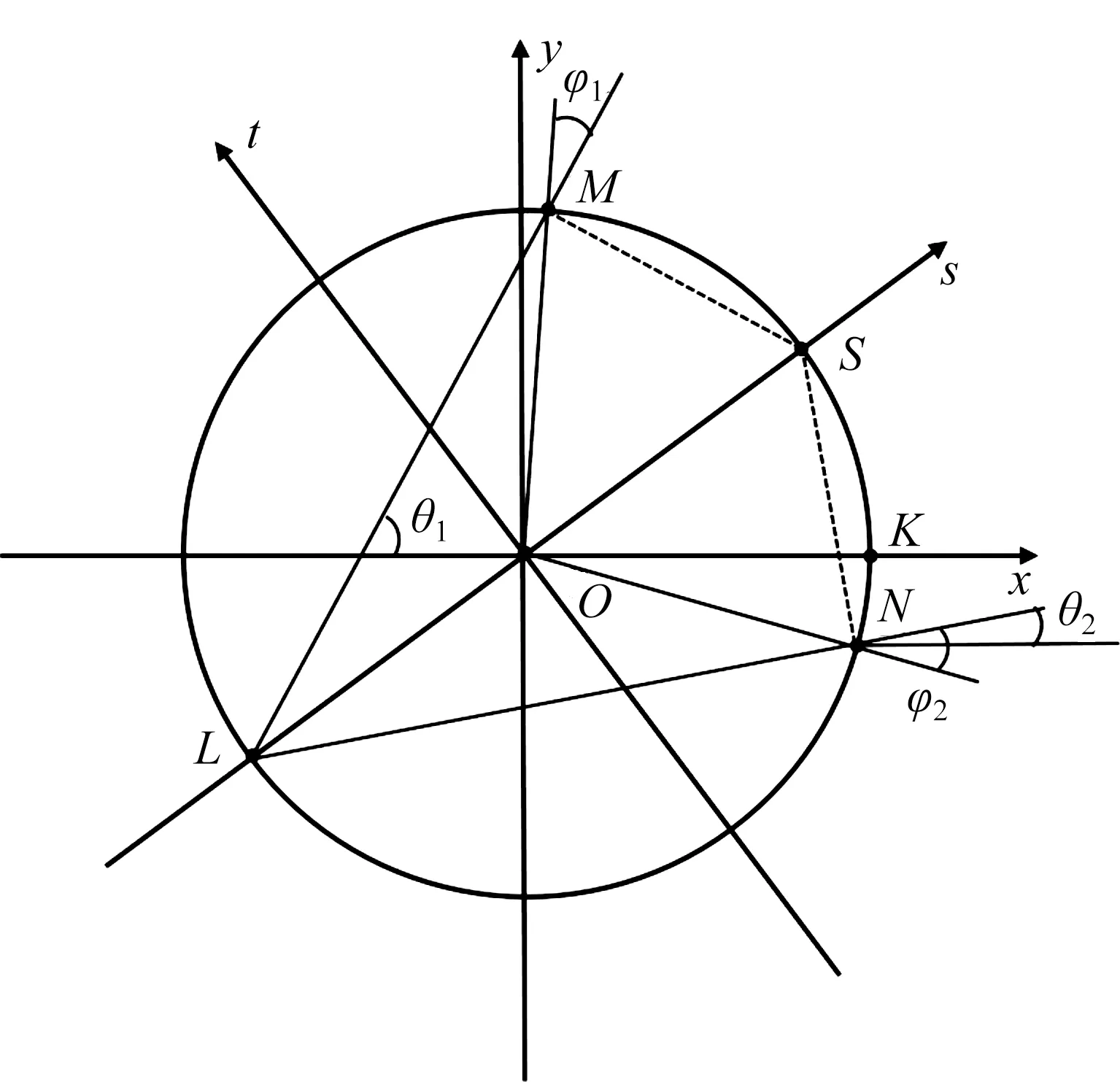
图8 x-y坐标系重绘模型Figure 8 Redrawn model in x-y coordinate system

阈值分割是一种应用于图像处理领域常用的图像分割的方法，主要将图像以定义的阈值为界进行二值化分割。在重绘的偏振角图像中子午线为一条直线且子午线上的每个点对应的大小接近90°。因此本文将使用阈值分割的方法检测位于太阳子午线上的像素的坐标位置。定义阈值大小为σ，阈值分割表达式如下：

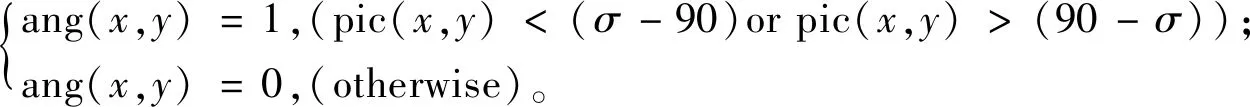
(12)

其中，pic(x，y)为重绘偏振角度图，ang(x，y)为分离后的二值图像。

偏振角度图是以子午线方向建立的坐标系重绘的，不同旋转角度拍摄的子午线以偏振角图像正中心为中心点旋转，因此子午线必经过图像中心点即原点。如图9，从偏振角图像中提取出所有偏振角接近90°的特征点坐标，以(0，0)点为中心进行过定点直线拟合。拟合完成的直线对应当前太阳子午线的方向即图10中的o-sun方向。斜率的倒数转化为角度对应太阳相对相机的方位角，在xoy相机坐标系中用αS表示。而地理坐标系中的太阳方位角φS可以通过当地的时间和经纬度计算。根据图10可得知，航向角φ可根据φS和αS求解，即

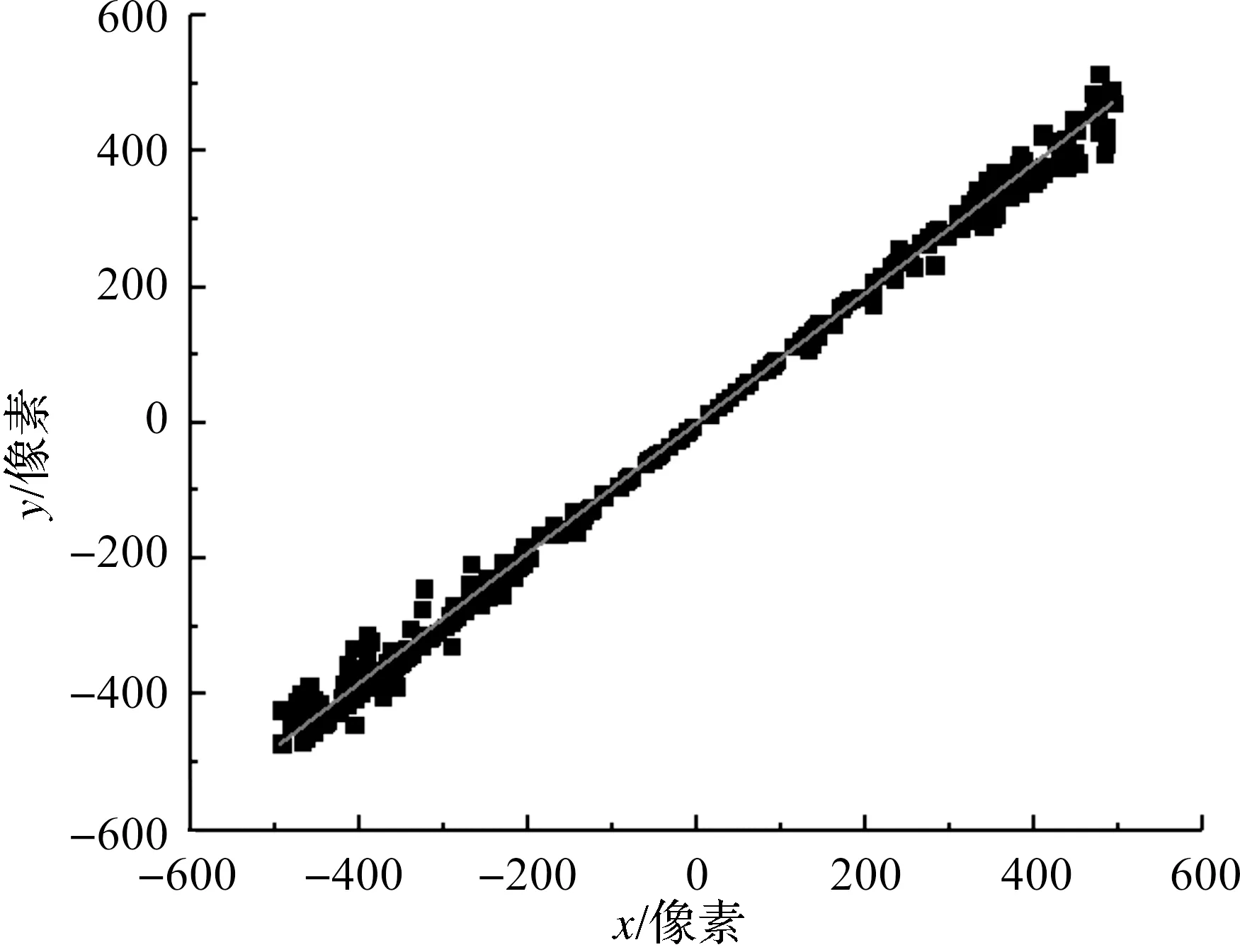
图9 特征点提取拟合Figure 9 Extracting and fitting feature points

φ=φS-αS。

(13)

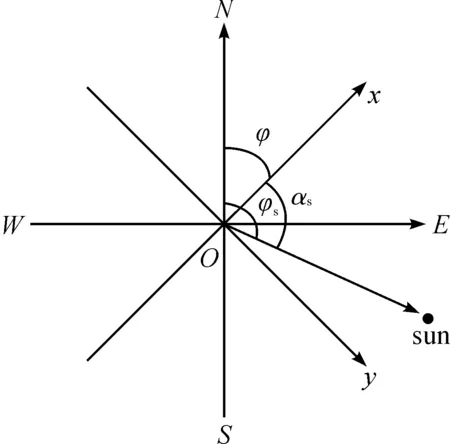
图10 航向角求解示意图Figure 10 Schematic diagram of heading angle solution

除了基于图像的航向角计算方法之外，胡小平团队提出了一种基于特征向量的太阳矢量估计方法[16]，只需要一张初始图片即可实现航向角解算，无需对图片进行多次处理。将该方法应用在像素偏振阵列时，以相机和观测方向建立相机坐标系和入射光坐标系，以0°，45°，90°和135°四个像素点为一个2×2测量单位，可测得一百二十五万个垂直于太阳矢量且不相关的E矢量，从中可求得太阳矢量最优解，进一步得到太阳相对相机坐标系的方位角αS，再根据式(13)计算得到航向角。本文将该方法用于后续的导航精度对比试验。

3 测试实验与分析

为了检测偏振导航相机的性能和航向角解算方法的精度，我们在室外进行了测试实验。实验地点位于周围无树叶、高楼等遮挡物的空旷楼顶上，测试时间为2019年6月29日16点30分，天气晴朗。测试装置如图11，电脑用于数据处理和储存；220V电源用于供电；POE交换机用于偏振相机供电和数据传输；偏振相机用于数据采集；精密转盘用于控制相机转动角度。偏振导航传感器以微偏振整列芯片为水平面水平固定并放置在精密转盘上，将传感器调整至体轴正北朝向，调整镜头光圈至合适大小以避免图片过渡曝光。使用指南针确定正北方向，以正北方向为起始方向0°作为起始点开始测试，以10°为单位断旋转传感器直至360°，每次旋转时采集一次图片共采集37张偏振图片。

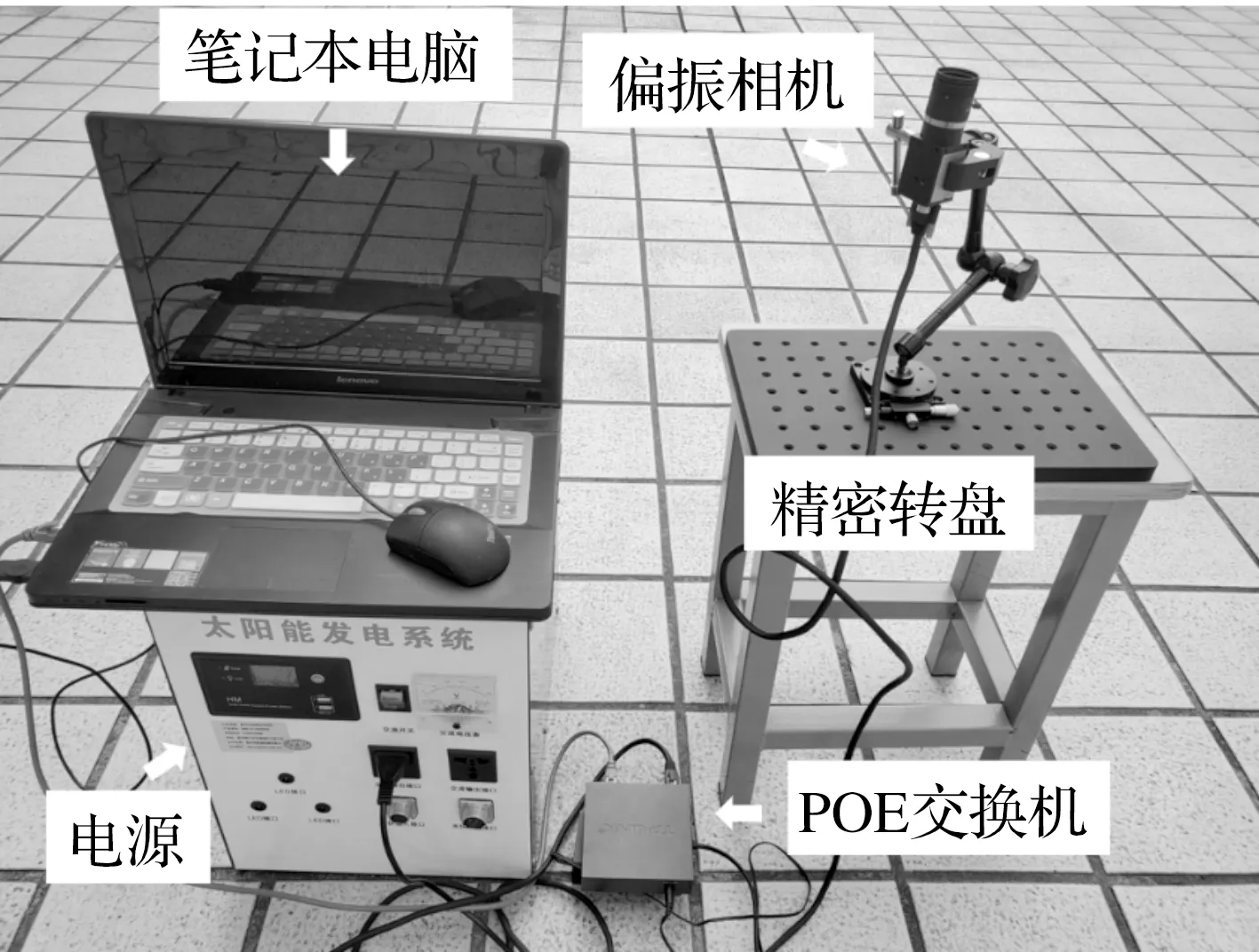
图11 实验装置Figure 11 Experimental device

使用基于图像的航向角计算方法(以下简述为方法1)将拍摄的37幅偏振分布图坐标重绘后，提取出子午线上的坐标点进行直线拟合，求解出方位角，经实验测试分析在阈值σ取0.1时拟合的直线精度较高。使用基于特征向量的太阳矢量估计方法(以下简述为方法2)同样对拍摄的37幅图片进行方位角解算。方法1和方法2计算得到的方位角为太阳相对相机坐标系的方位角，结合太阳地理方位角即式(13)解算得到航向角。太阳地理实际方位角可根据测试地点的经纬度和具体测试时间计算得到[17]。航向角与转盘旋转角误差可通过计算旋转角和航向角的差值得到，平均相对误差取相对误差绝对值的均值。两种方法的航向角计算误差曲线如图12，方法1的航向角误差均值为0.332°，最大误差为0.882°，系统的平均相对误差为0.374%；方法2的航向角误差均值为2.304°，最大误差为3.372°，系统的平均相对误差为2.11%。使用T检验对两种方法的平均误差的差异程度进行检验，计算得到P值远小于0.01，两者差异非常显著，因此可以断定使用方法1时的整体计算精度大于方法2。

方法1中偏振相机在旋转角度为20°、110°、200°和290°时误差较大，结合4个旋转角度对应的偏振角度图发现，四幅图中子午线都与微偏振阵列中标定的坐标轴接近重合。经分析是在直线拟合过程中定义直线方程截距为0所导致。拟合算法在定义截距为0时自动排除位于坐标轴上的所有坐标点，因此产生一定的角度误差。在计算坐标轴方向的子午线角度时，将阈值调整至0.01计算出的航向角误差有所降低。

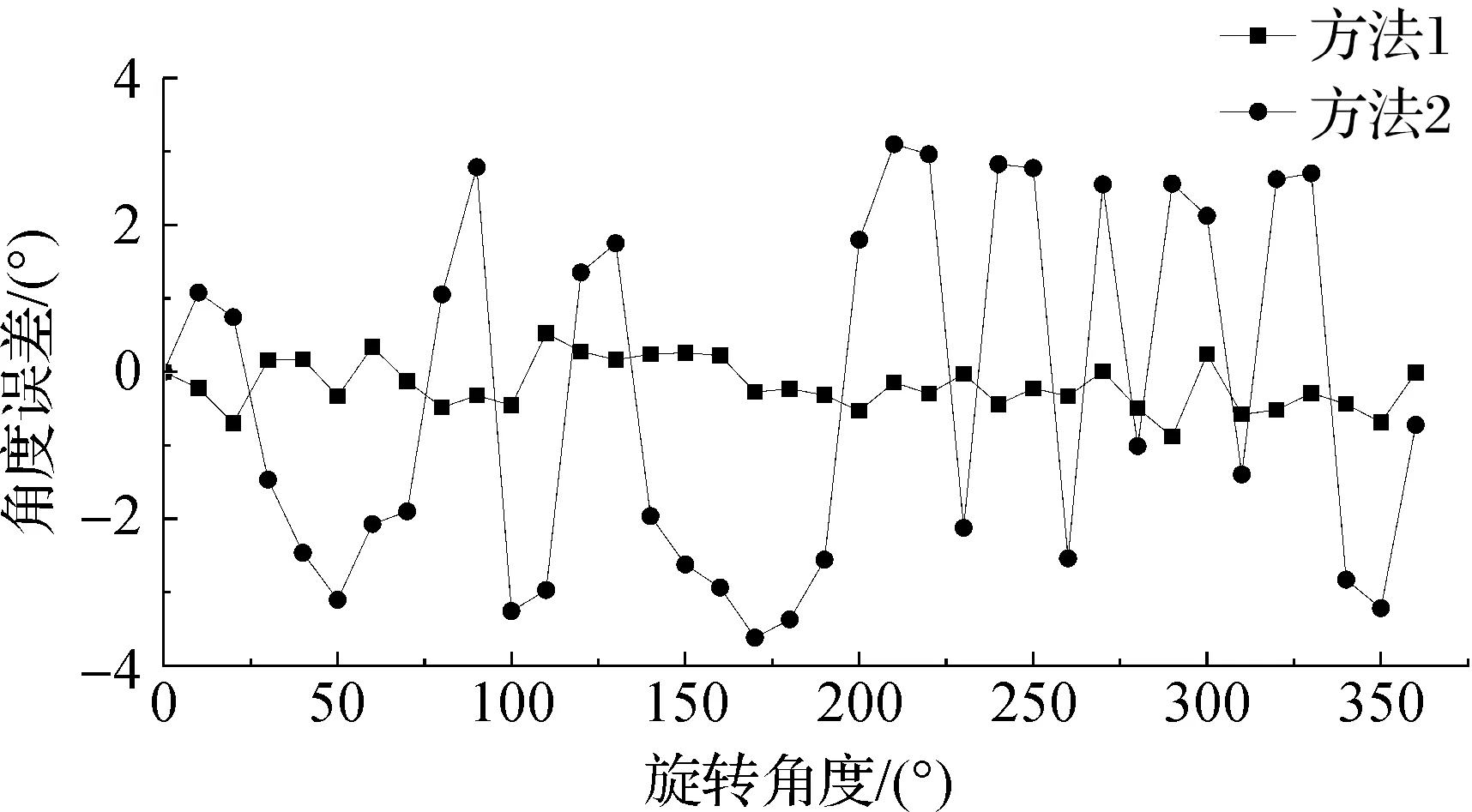
图12 航向角误差曲线Figure 12 Heading angle error curve

4 结 论

本文基于像素偏振阵列结构芯片和相机镜头搭建了一款偏振导航传感器，应用了两种航向角计算方法：基于图像的航向角计算方法和基于特征向量的太阳矢量估计方法。在基于图像的航向角计算方法中，针对偏振角度原始图片无法辨别子午线的问题，采用坐标重绘的方法重绘偏振角图片，提取出子午线上对应的坐标点进行拟合并解算出航向角。使用传感器进行了户外测试实验和对两种航向角解算方法进行精度对比，实验结果表明该传感器在采用基于图像的航向角计算方法时精度较高。该偏振导航传感器具有精度高、体积小的优点，户外航向角测试的误差均值为0.332°，只需拍摄一张照片即可完成单次航向角检测，连续拍摄即可实现航向角的实时跟踪，从而实现导航，导航精度满足户外导航系统要求。