温度应力对低碳微合金钢连续冷却过程中相变塑性的影响

庞博文，丁文红，孙 力，张志强，潘 进，袁 飞

(1.武汉科技大学省部共建耐火材料与冶金国家重点实验室，湖北 武汉，430081；2.河钢集团钢研总院，河北 石家庄， 050023；3.河钢集团邯钢公司技术中心，河北 邯郸，056002)

近年来，随着低碳微合金钢生产过程中超快冷技术的应用，由温度梯度和相变不同步所引起的带钢高残余应力问题已成为制约钢种发展的关键所在，因此，有必要对高强钢在连续冷却过程中残余应力的形成机理及影响因素进行探究。

金属材料组织转变过程中，当在低于弱相屈服强度的载荷作用下，材料会发生不可逆的塑性变形行为，即相变塑性[1]。作为区别于经典塑性变形的不可逆变形，现阶段关于其机理的解释主要包括基于扩散机制的Greenwood-Johnson模型[2]和基于择优取向效应的Magee模型[3]。另一方面，随着计算机模拟技术的发展，国内外研究者已结合有限元模拟和试验，分析了不同热处理工况(如焊接、淬火)下相变塑性对工件残余应力分布的影响规律[4-7]。而带钢快速冷却过程中，由温度梯度形成的温度应力为相变塑性效应的发生提供了可能，但目前有关这方面的研究还报道较少。前期，本课题组采用单轴载荷热拉伸/压缩实验模拟实际工况的温度应力，研究了连续冷却过程中温度应力对低碳微合金钢H420LA相变塑性和相变动力学的影响，结果表明，在小于母相屈服强度的外加单轴载荷作用下，试验钢铁素体相变开始温度降低，表现为奥氏体力学稳定化现象[8-9]，这一结论与文献[10]报道的等温冷却过程中外加单轴载荷会促进铁素体/珠光体相变存在差异；另外，随着外加载荷的增加，材料相变迟滞时间缩短，这种应力作用下的相变迟滞效应也可能对相变过程中材料残余应力的演变产生影响[8-9]。

基于本课题前期研究结果，本文拟采用单轴热模拟拉伸/压缩实验，研究汽车大梁钢700L在连续冷却条件下，温度应力对铁素体相变塑性和相变动力学的影响规律。

1 相变塑性的试验测定

1.1 试验方法

单轴热拉伸/压缩试验在Gleeble 3500热模拟试验机上进行，具体步骤为：将焊有热电偶的试样装机，腔内抽真空并充入氩气，以10 ℃/s的升温速率将试样加热至1000 ℃，保温5 min以保证其充分奥氏体化，随后以10 ℃/s的速率冷却试样，至760 ℃时进行加载(1 s内完成)，载荷分别为±15、±30、±45、±60 MPa(“+”表示拉伸载荷，“-”表示压缩载荷)，保持加载状态直至冷却至室温，冷却速率恒定为10 ℃/s，并记录试验过程中时间、温度、膨胀量、载荷等数据。陈银莉和邱增帅等[11-12]对热轧带钢层流冷却后温度场的研究结果表明，带钢沿宽度方向边部和中部的温差为40～61 ℃，该温度差会产生约130 MPa的温度应力。因此，为探究温度应力对700L钢相变塑性的影响规律，所加载荷均不超过相变期间奥氏体屈服强度的1/2。

表1 700L钢的化学成分 (wB/%)

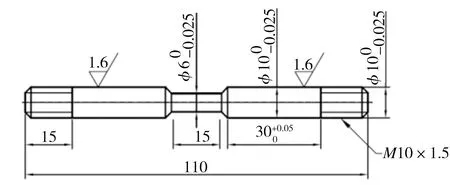
(a) 拉伸试样

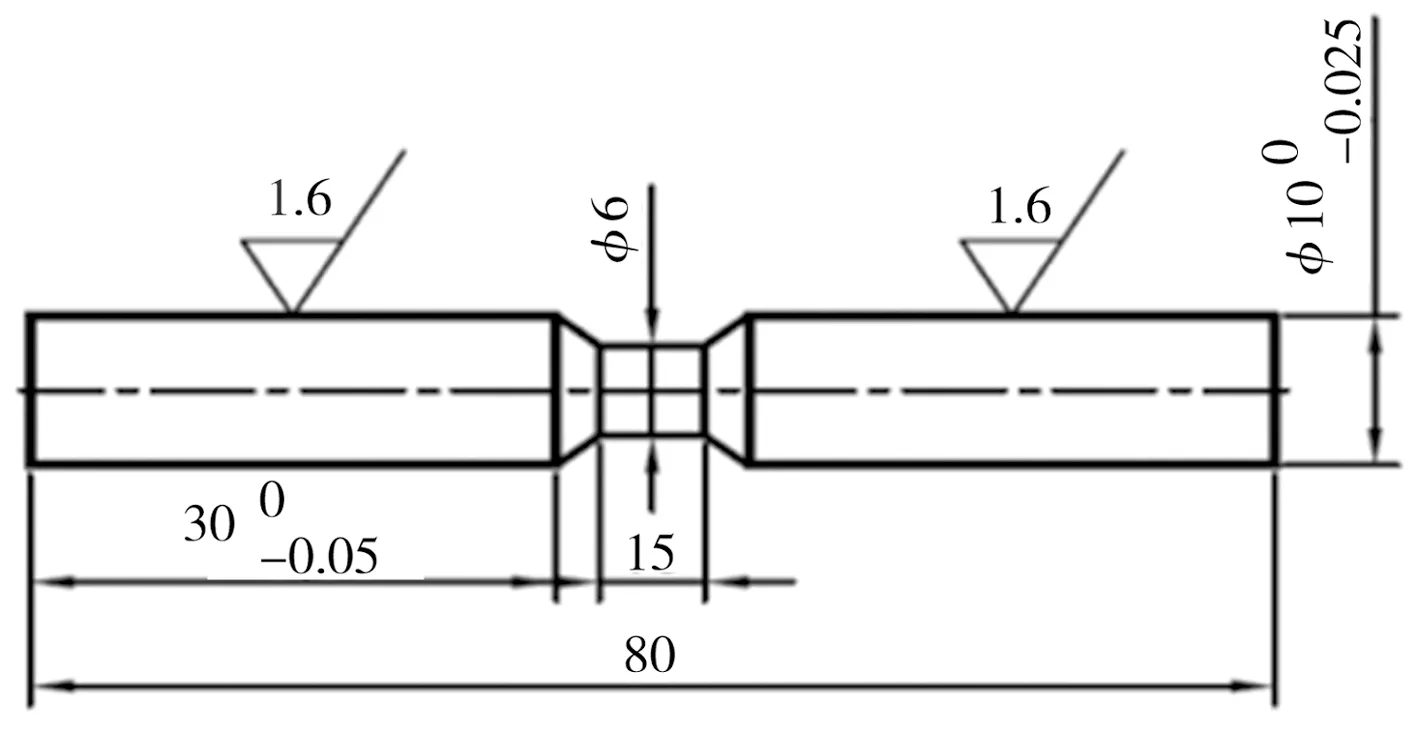
(b)压缩试样

1.2 相变塑性应变的计算

铁素体连续冷却过程中，由于受到相变塑性的影响，有外力作用和无外力作用的径向膨胀曲线存在明显差异。载荷作用下的总应变ε(σ)由温度变化引起的热应变εth、组织转变应变εtr、弹性应变εe、塑性应变εp以及相变塑性εtp应变组成，可写作：

ε(σ)=εth+εtr+εe+εp+εtp

(1)

(1) 热应变及组织转变应变

任意温度条件下，无应力作用下试样的膨胀量ε为该温度下组织转变引起的膨胀量与温度变化引起的热膨胀量之和，即：

ε=εth+εtr

(2)

本研究中，700L钢在连续冷却过程中(冷速10 ℃/s)仅发生了铁素体转变，且根据如图2所示的金相照片可知，700L钢相变完成后的室温组织主要为铁素体，贝氏体和残余奥氏体量极小。

故假设在相变完成时组织完全转变为铁素体，那么热应变可表示为：

εth=ξαFT+(1-ξ)αA(T-T′)

(3)

式中：ξ为铁素体转变量，αF为铁素体相变膨胀系数，αA为奥氏体的热膨胀系数，T为实际温度，T′为参考点温度。

无外力作用下，带钢的相变膨胀系数与温度的关系为：

βF(T)=βF,T′+(αF-αA)(T-T′)

(4)

式中：βF(T)为温度T时铁素体的相变膨胀系数，βF,T′为温度T′下铁素体相变完成时的铁素体相变膨胀系数。

温度T下试样的相变应变εtr可表示为：

εtr=βF(T)ξ=[βF,T′+(αF-αA)(T-T′)]ξ

(5)

(2)弹性应变

弹性应变遵循胡克定律，其主要取决于外加载荷大小和不同温度下的弹性模量，即：

(6)

E(T)=EF(T)ξ+EA(T)(1-ξ)

(7)

式中：μ取0.3(弹性范围内)，σ为施加载荷大小，E(T)、EF(T)和EA(T)分别表示温度T时试样、铁素体和奥氏体的弹性模量。

700L钢弹性模量及屈服强度随温度的变化曲线如图3所示。为方便计算，取室温下的弹性模量和高温时的弹性模量进行拟合，得到700L钢弹性模量关于温度的函数：

E(T)=268.757 97-0.232 24T

(8)

Fig.3 Curves of elastic modulus and yield stress variation with temperature of 700L steel

(3)经典塑性应变

当外载小于奥氏体在加载温度下的屈服强度时，试样不产生经典塑性变形，此时：

εp=0

(9)

(4)相变塑性应变

由体积不变原理可知：

εtp,r=-0.5εtp

(10)

式中：εtp,r表示材料径向的相变塑性应变，εtp为材料轴向的相变塑性应变。

以30 MPa压应力为例，假设有外应力和无应力作用时，由温度引起的热应变和组织转变引起的相变应变相同，根据式(1)和式(2)，用30 MPa下的相对径向膨胀量减去无应力作用下的相对径向膨胀量，得到该应力条件下径向弹性应变和相变塑性应变之和，其随温度变化如图4(a)所示。又由式(6)～式(8)，得到700L钢径向弹性应变随温度的变化曲线如图4(b)所示。根据上述结果，利用图4(a)对应的应变量减去图4(b)中各温度对应的弹性应变量，可分离得到30 MPa载荷作用下材料的径向相变塑性应变，根据式(10)，换算得到30 MPa压应力作用下材料的轴向相变塑性应变与温度关系如图4(c)所示。同理，通过相变塑性应变分离，得到各载荷作用下700L钢轴向相变塑性应变与温度关系如图5所示，图中曲线平台对应的应变即为相变塑性所产生的应变。由图5可知，在不同的载荷作用下，试验钢均会发生明显的相变塑性变形。

(b) εe-T

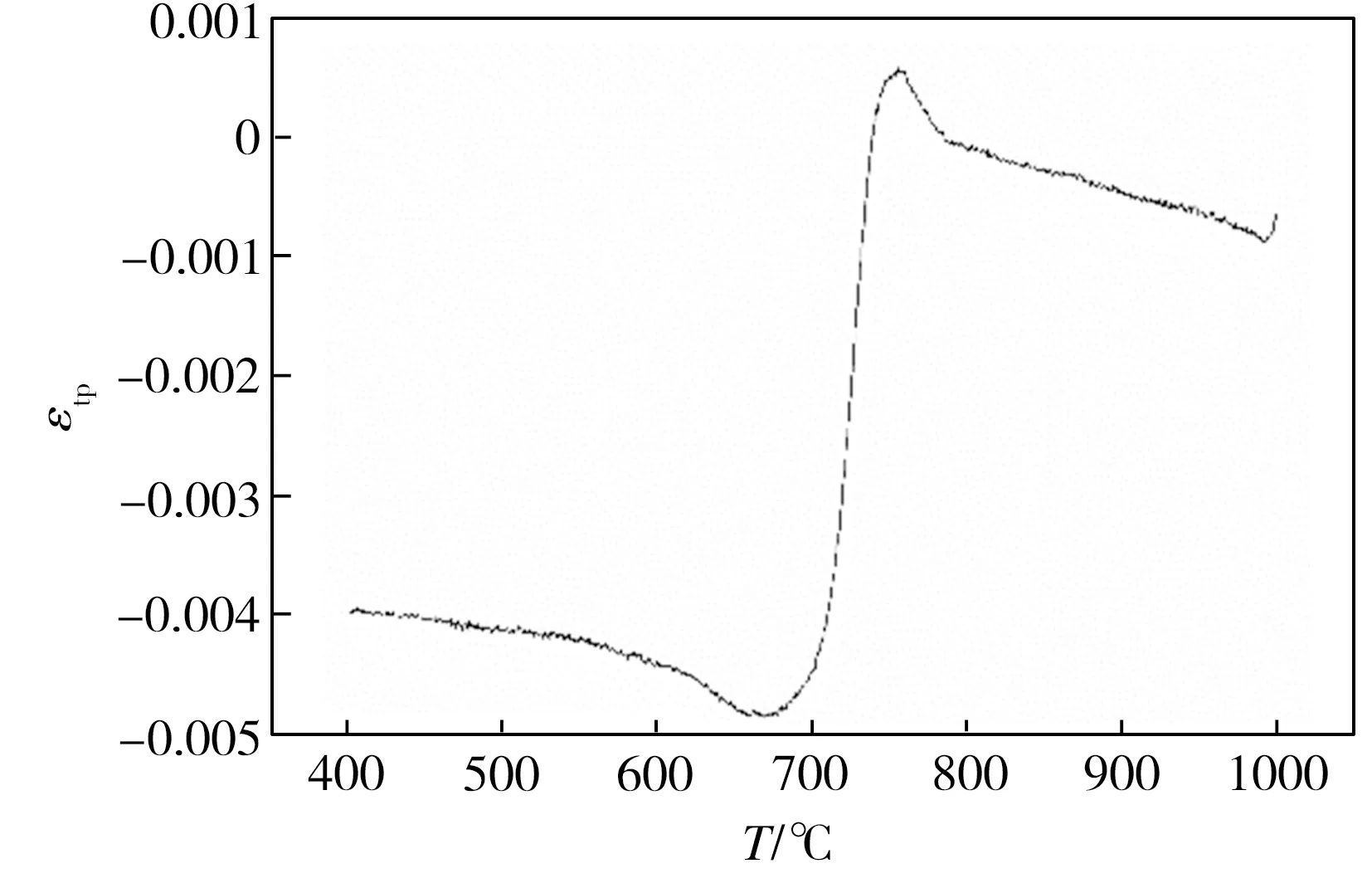
(c) εtp-T

Fig.4 Relationship between strain and temperature of 700L steel under 30 MPa compressive stress

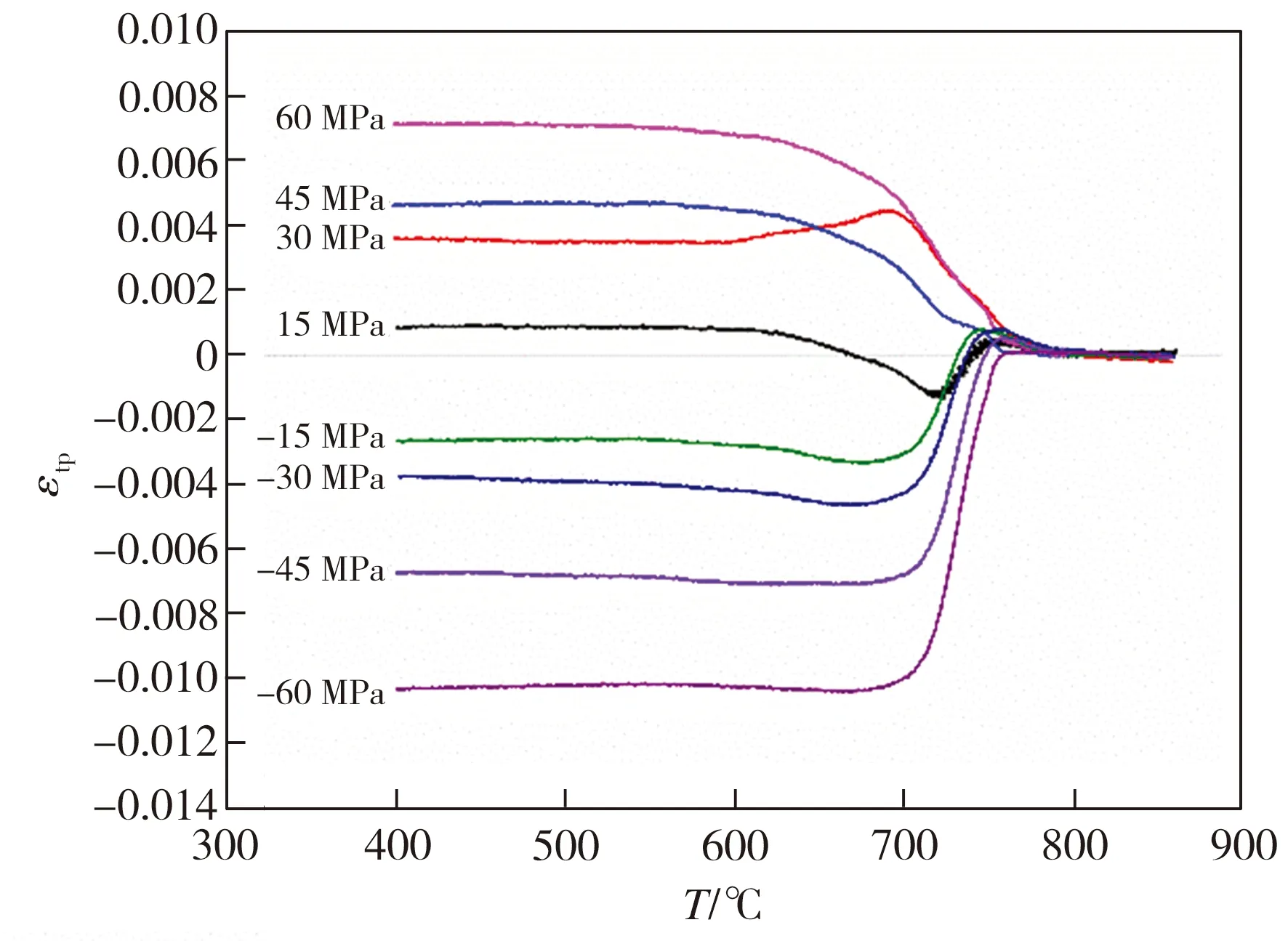
图5 不同单轴载荷下700L钢相变塑性应变与温度的关系

Fig.5 Relationship between transformation plastic strain and temperature of 700L steel under different uniaxial loads

2 结果与分析

2.1 温度应力对700L钢相变塑性的影响

不同载荷作用下700L钢的相变塑性应变量如图6所示。由图6可知，700L钢的相变塑性应变与载荷作用方向存在相关性，即压应力作用产生负的相变塑性应变，拉应力作用产生正的相变塑性应变，这是因为相变塑性是当材料在小于弱相屈服强度的应力作用下，伴随相变过程所产生的不可逆塑性应变，是塑性应变在应力方向上的累加，故与应力作用方向存在一致性。Taleb等[13]在16M5ND钢的马氏体相变规律研究中也发现了类似现象。从数值上看，相变塑性应变与载荷呈正相关关系，随着载荷增加，相变塑性应变也随之增加。从载荷作用效果上看，在小载荷(15 MPa)作用下，压应力对材料相变塑性的作用效果最显著，其相变塑性应变是同数值拉力载荷的3.26倍；随着载荷增加至30 MPa，压应力与拉应力作用效果几乎相同；但随着载荷进一步增大至45、60 MPa，压应力所引起的相变塑性应变与拉应力条件下相应值相比，分别提高了约46.7%和45.2%，整体而言，压应力对材料相变塑性的影响效果更显著。基于Denis等[14]改进的Greenwood-Johnson模型表征材料相变塑性应变，得到应力对相变塑性应变的一般影响规律，即：

εtp=kσξ(2-ξ)

(11)

式中：k为相变塑性参数，σ为外加单轴载荷。

当铁素体转变完全时ξ=1，上式可简化为：

εtp=kσ

(12)

由于拉应力与压应力的作用规律相同，根据式(12)和试验数据拟合得到相变塑性参数k，如表2和图6中直线所示，可以看出，材料的相变塑性应变与加载应力呈近似线性关系，直线斜率即为相变塑性系数，k=1.357×10-4。这也验证了Leblond[1]的观点：当应力小于相变温度下奥氏体屈服强度的1/2时，材料相变塑性应变与应力呈线性关系，即k为常数。

表2 不同单轴载荷作用下700L钢的相变塑性参数

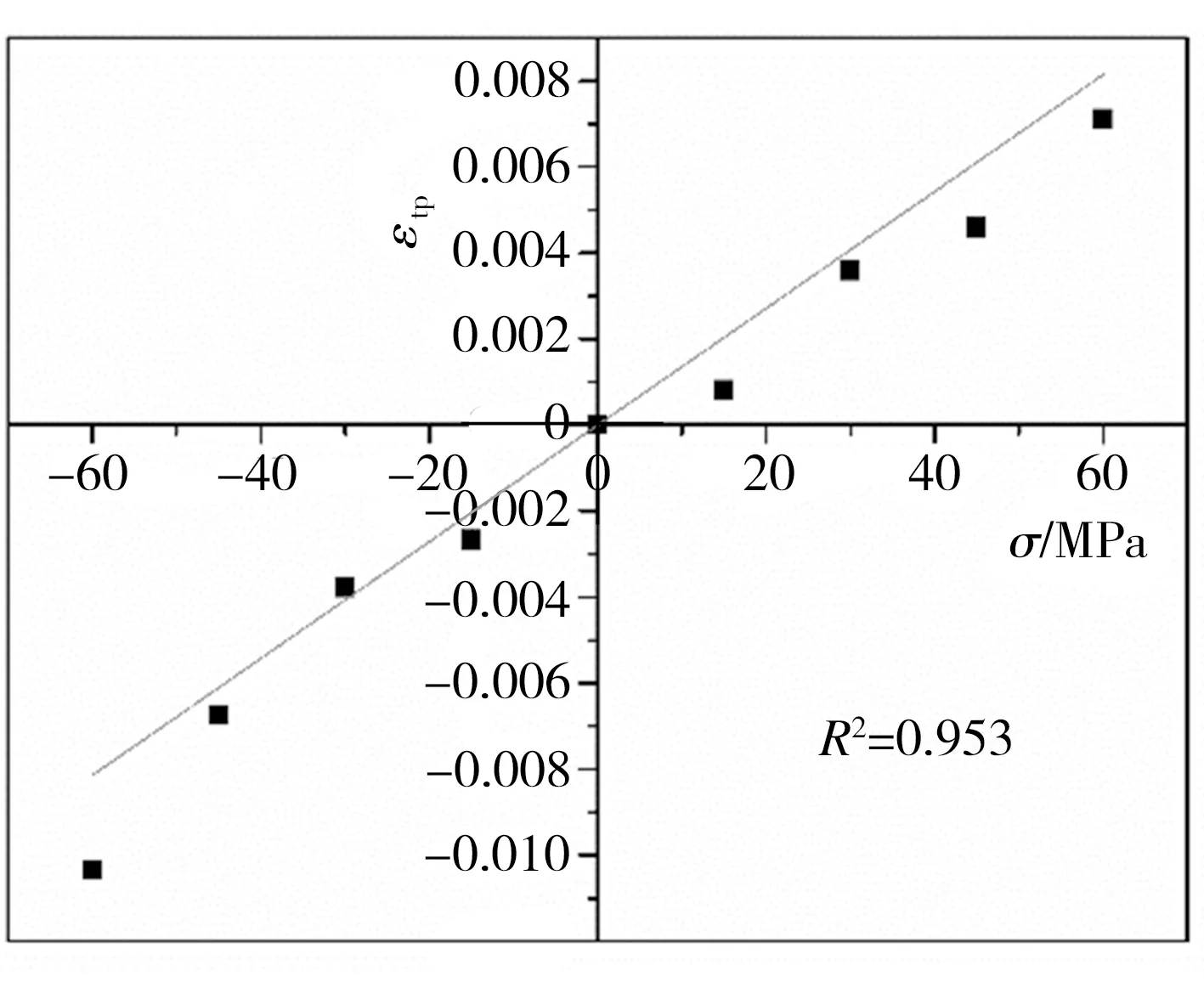
图6 700L钢相变塑性应变与单轴应力的关系

Fig. 6 Relationship between transformation plastic strain and uniaxial load of 700L steel

2.2 温度应力对700L钢相变动力学的影响

结合图7和表3可见，相比于无外加载荷的情况，在单轴拉应力与压应力作用下700L钢的相变起始温度有所降低，即产生迟滞效应，这与文献[9]报道的外加载荷对H420LA钢铁素体相变起始温度的影响规律一致，并且Schicchi等[15]在大应力作用下22MnB5钢的贝氏体转变过程中也观察到类似现象。另外，在小外应力下，700L钢的相变滞后效应更显著，随着外加载荷的增加，相变滞后时间大致呈缩短的趋势。从表3还可以看出，单轴拉/压载荷作用明显缩短了试验钢的相变反应时间，且拉应力的作用效果更明显，当外加载荷为+60 MPa时，700L钢的相变反应时间最短为9.1 s。

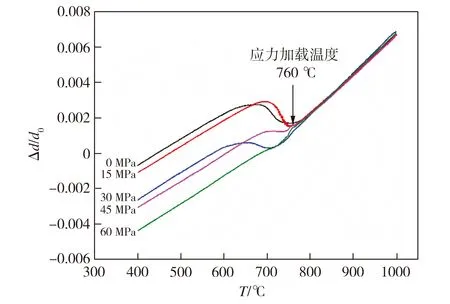
(a)拉伸载荷

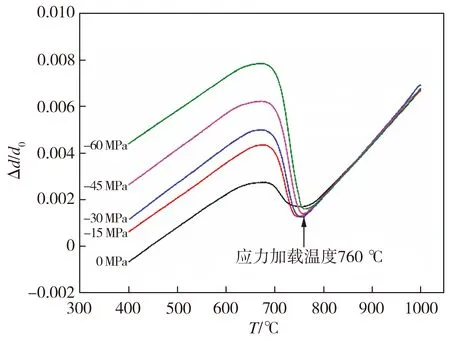
(b)压缩载荷

图7 不同单轴载荷作用下700L钢总应变与温度的关系

Fig.7 Relationship between total strain and temperature of 700L steel under different uniaxial loads

表3 不同单轴载荷作用下700L钢的相变温度与相变时间

根据杠杆定律，计算得到不同单轴拉/压载荷作用下700L钢铁素体转变量与温度关系如图8所示。由图8可见，不同压应力作用下，700L钢连续冷却过程中的相变动力学曲线均呈“S”型。相比于无外应力作用的情况，在相变开始的高温阶段，外应力作用下钢中铁素体转变速率相对较小，但随着相变的持续进行，有外应力作用时钢中铁素体转变速率明显增加，且压应力越大，铁素体转变速率越快，即对应图8(b)中曲线的斜率越大。由此可见，单轴压应力可以促进钢中铁素体相变，缩短反应时间。整体而言，大外加载荷作用下的加速效果更显著。本课题组前期研究从H420LA钢热轧板连续冷却过程的铁素体相变中也观察到类似现象[8-9]。

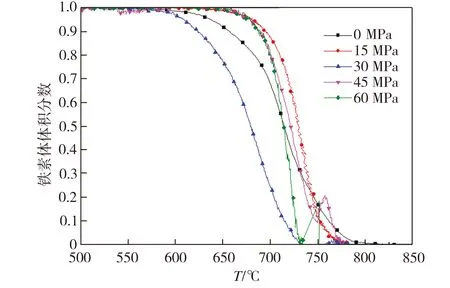
(a)拉伸载荷

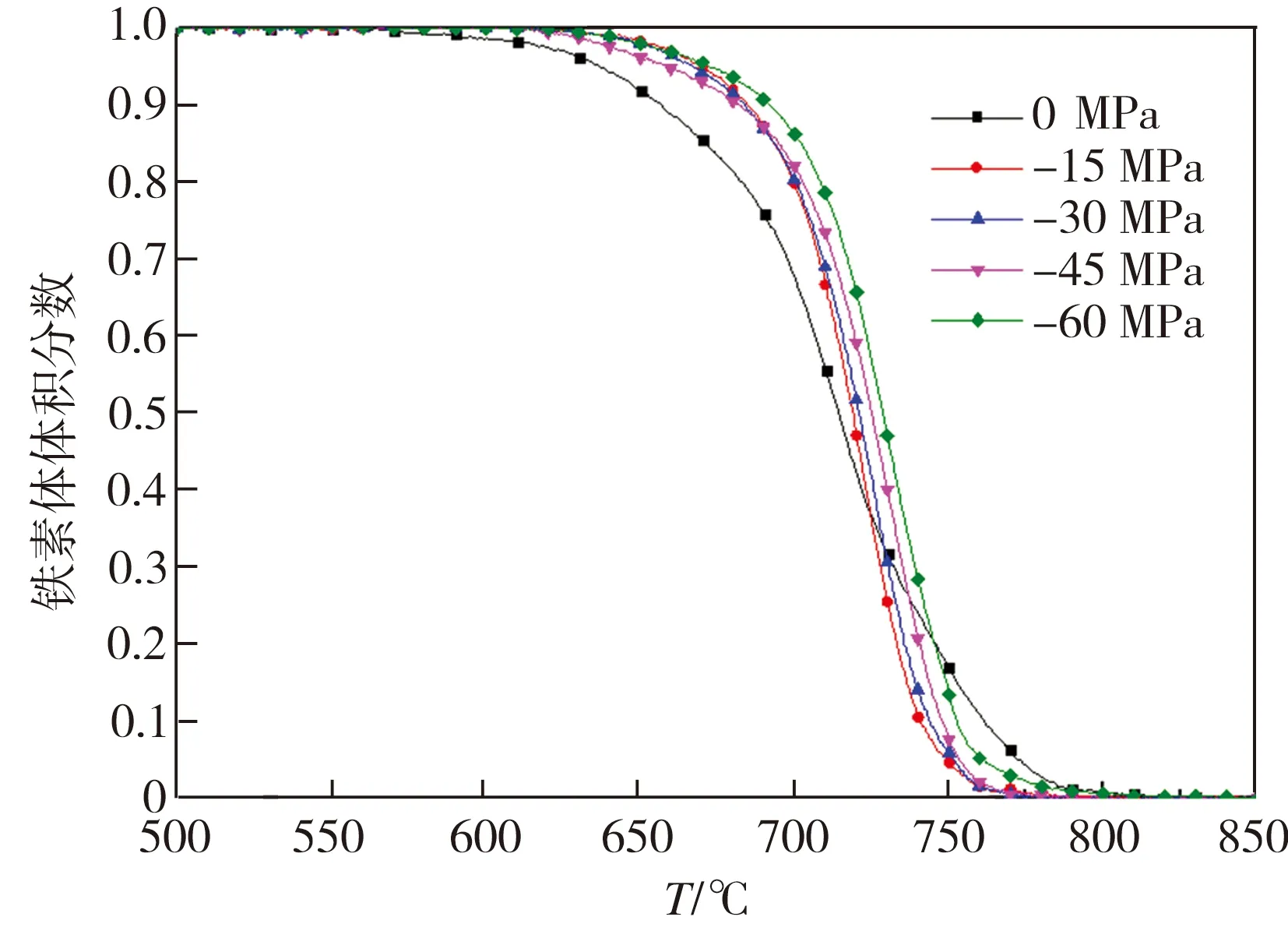
(b)压缩载荷

Fig.8 Effect of uniaxial load on the transformation kinetics of 700L steel

另外，对于30 MPa拉应力作用下700L钢的铁素体相变过程而言，从相变反应时间来看，其相比于无应力作用时的情况有所缩短，但与其他拉应力条件下相比，其相变反应时间又相对较长，且动力学曲线整体向左偏移，该反常现象有待进一步探究。

3 结论

(1)温度应力对700L钢的相变塑性有重要影响，即拉应力产生正的相变塑性应变，压应力产生负的相变塑性应变。

(2)在小应力范围 (奥氏体1/2屈服强度范围内)，700L钢的相变塑性应变与单轴载荷呈线性关系，相变塑性系数k=1.357×10-4。

(3)从载荷作用效果上看，整体而言，压应力对700L钢相变塑性的作用效果更显著。

(4) 温度应力对700L钢相变动力学有显著影响，外加载荷作用降低了700L钢的相变开始温度，推迟了相变开始时间，且随着外应力的增大，相变滞后时间大致呈缩短的趋势；根据700L钢的相变动力学曲线可知，温度应力缩短了奥氏体向铁素体转变的反应时间，即加速了相变进程，并且拉应力的作用效果更为显著。