采用双经验回放池的噪声流双延迟深度确定性策略梯度算法

王垚儒，李 俊

(1.武汉科技大学计算机科学与技术学院，湖北 武汉，430065；2.武汉科技大学智能信息处理与实时工业系统湖北省重点实验室，湖北 武汉，430065)

强化学习(Reinforcement Learning，RL)方法通过智能体与环境进行交互，观测到环境对智能体动作的反馈后，不断调整其行为，以提升自身性能。但传统的强化学习局限于低维问题，深度强化学习则能更好地处理高维状态空间和高维动作空间设定下的决策问题，并已广泛应用于电脑游戏、机器人控制、语音识别、交通信号控制、自动驾驶等领域[1]。

文献[2-3]将强化学习与深度学习相结合，提出深度Q网络(Deep Q-network, DQN)模型，该模型用于处理基于视觉感知的控制任务，是深度强化学习研究领域的开创性工作。之后，很多拓展性方法不断出现，以提升DQN算法的速度和稳定性。文献[4]使用优先经验回放技术有效提高了学习效率。文献[5]采用深度双Q学习策略，通过解耦选择和引导行动评估解决了Q学习中的过估计问题。文献[6]结合多步Q学习和深度Q学习的优点，提出了深度多Q学习方法，其稳定性较好且更具有普适性。文献[7]构建竞争网络结构，采用两条支路分别估计状态价值和动作优势，这样一来，对于各个状态就不必评估每个动作选项产生的效果，进一步提高了智能体的学习效率。文献[8]提出噪声流深度Q学习策略，使用随机网络层进行勘测，增强了网络探索性能。文献[9]提出Rainbow算法，结合多种DQN的改进方式，在不同层面上提高了算法性能。然而，DQN算法难以应对大的动作空间，特别是在连续动作情况下。

文献[10]提出的深度确定性策略梯度算法(Deep Deterministic Policy Gradient, DDPG)算法是表演者-评论家(Actor-Critic，AC)框架和 DQN 算法的结合体，其在动作输出方面采用一个网络来拟合策略函数，可以很好地应对连续动作的输出及大的动作空间。文献[11]提出混合型Actor-Critic指导方法，融合了多个策略网络和对应的值网络，该方法在自适应机器人控制中取得了实质性进展。文献[12]采用循环确定性策略梯度和循环随机值梯度方法，处理一系列部分可观察场景下的连续动作控制任务。文献[13]中提出的异步优势表演者-评论家算法(Asynchronous Advantage Actor-Critic，A3C)降低了训练时的硬件要求，在各类连续动作空间的控制任务中表现较好。文献[14]提出的双延迟深度确定性策略梯度算法(Twin Delay Deep Deterministic Policy Gradient，TD3)是以深度双Q学习为基础，采用双评论家，选取其中较小的值来平衡价值，并延迟更新策略网络，以减少更新错误，同时为目标行为增加噪声，用作算法的正则化器。TD3算法很好地解决了DDPG中估计价值过高的问题，但是网络的收敛速度和探索性能仍有待提高。

本文提出一种基于多步优先和重抽样优选双经验回放池的噪声流双延迟深度确定性策略梯度算法(简记为MPNTD3)，在策略网络中添加噪声以增加参数的随机性，并引入多步优先经验回放池和重抽样优选经验回放池。考虑多步回报，利用优先级更高的样本来更新当前的目标值，可解决噪声网络难以收敛的问题，同时引入重抽样优选经验池和多步优先经验回放池则在一定程度上弥补了重抽样优选机制中低优先级样本不足的缺点。本文最后在OpenAI Gym仿真平台上的Walker2d-v2场景中进行实验，以检验MPNTD3算法的性能。

1 相关知识

1.1 DQN算法

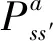
(1)

式中：γ为折扣因子；E[·]代表期望值。

当时间步数i→时，当前状态-动作值Qi收敛到最优。在实际应用中，通常使用函数逼近的泛化方法近似估计Q*(s,a)，即Q*(s,a)≈Q(s,a;θ)。DQN算法采用卷积神经网络函数近似器，这时θ代表网络权重。参数θ可通过最小化损失函数的方式进行计算，损失函数定义为：

Li(θi)=Es′～S[(yi-Q(s,a;θi))2]

(2)

其中，

(3)

在网络参数θi-1保持不变的情况下，优化损失函数Li(θi)。对损失函数的参数进行微分得到梯度公式:

Q(s,a;θi))θiQ(s,a;θi)]

(4)

然后通过求解Bellman方程得出最优策略。

DQN算法中最关键的技术就是经验回放，即设置经验池。将每个时间步中智能体与环境交互得到的转移样本(s,a,r,s′)储存到回放记忆单元，然后随机取出一些样本进行训练，这种将过程打成碎片存储、训练时随机抽取的方式可以避免相关性问题。

1.2 DDPG算法

DDPG算法是在Actor-Critic框架的基础上，基于DQN的经验回放和双网络结构对确定性策略梯度算法进行改进[15]。双网络结构的方法是指构造结构相同而参数不同的基于Actor-Critic框架的估值网络和目标网络，采用经验回放方法对目标网络参数进行更新。确定性策略可以描述为在状态s下采取的确定性动作a，动作值函数表示在状态s中采取a之后的预期回报，使用参数为θμ和θQ的神经网络来表示确定性策略a=μ(s|θμ)和值函数Q(s,a|θQ)。

目标网络输出为目标Q值(Qtarget)，估计网络输出为估计Q值(Qtarget)，记二者的差值为TD-error，Critic 网络训练基于TD-error 的平方均值。估计Q值是将当前的状态s和估值Actor网络输出的动作a输入估值Critic网络得到，而目标Q值是将下一时刻的状态s′及由目标Actor网络所得动作a′输入到目标Critic网络后得到的Q值进行折扣后与目标奖励r相加得到。具体公式如下：

yi=r+γQ(s′,μ(s′|θμ′)|θQ′)

(5)

(6)

式中：yi为目标Q值；Q(s,a|θQ)为估计Q值；L为TD-error 的平方均值。

估值Actor网络通过动作值函数将状态映射到指定动作来更新当前策略，状态回报定义为未来折扣奖赏总回报，通过David Silver策略梯度方法对目标函数进行端对端的优化, 从而朝着获得最大总回报的方向更新。Actor网络参数更新公式如下：

(7)

1.3 TD3算法

针对DDPG算法中估计价值过高的问题，TD3算法采用截断双Q学习、目标策略平滑处理、延迟更新策略三种方法来平衡价值。

截断双Q学习是将原来的一个Q函数分为两个，这两个Q函数都针对单目标更新，选择其中较小的一个作为目标值,这样有助于抵消Q函数中的过高估计，具体公式如下：

(8)

(9)

(10)

式中：d表示环境状态，为布尔型变量，若当前动作后整个过程结束，则d=True，否则d=False；D为训练样本集合。

目标策略平滑处理是基于目标策略μ得出目标动作，同时在动作的每个维度上添加扰动因子，使得目标动作a的取值满足条件:alow≤a≤ahigh，其中alow、ahigh分别表示动作a可取的最大值和最小值。目标策略平滑处理可表示为：

a′=clip(μ(s′)+o,alow,ahigh)

o～clip(N(0,σ),-c,c)

(11)

式中：clip(x,-y,y)表示将x中的每个元素截断到区间 [-y,y]中。

目标策略平滑处理为目标行为增加了噪声，用作算法的正则化器。它解决了DDPG中可能发生的如下特定故障模式：如果Q函数逼近器产生不正确的峰值，则上述方法将快速利用该峰值使Q函数变得平滑。

延迟更新策略是指，在TD3中Actor网络和目标网络参数的更新频率比Critic网络参数的更新频率要低，这有助于抑制DDPG中通常出现的波动现象。

2 本文算法设计

2.1 噪声网络

为了提高本文算法的网络探索性能，在策略网络的全连接层中添加噪声，以增强网络参数w、b的随机性。关于参数b和w的目标函数服从于均值为μ、方差为σ的正态分布，同时存在一定的随机噪声ε，并假设噪声服从标准正态分布N(0,1)，则新形成的到噪声层的前向传播方式如下：

y=(b+wx)+[bnεb+(wnεw)x]

=(w+wnεw)x+b+bnεb

(12)

式中：wn和bn为噪声层的权重和偏移量；εw和εb代表权重和偏移量的随机噪声。

添加噪声增加了参数的随机性，网络探索能力加强，网络的性能也会提高，但同时网络也会变得更加难以收敛。

本文采用两种方式来加快噪声网络的收敛。一是考虑多步回报，将截断双Q处理改为多步截断双Q处理，增加网络对于目标值的评估准确性；二是通过重抽样优选经验回放池，在训练后期使用学习价值更大的样本，使网络进一步收敛。

2.2 多步截断双Q学习

多步截断双Q学习是在截断双Q学习方法中利用将来多步信息来更新当前的目标值。TD3算法仅利用了未来一步的信息，存在更新速度慢的问题，而本文采用的多步截断双Q学习考虑未来n步的影响。

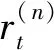
(13)

选择适当的n值可以提高网络的性能和收敛速度。

2.3 多步优先经验回放池

在截断双Q处理时要考虑多步回报，因此将优先经验回放池改进为多步优先经验回放池，即按照优先经验回放池的存储结构和采样方法将多个连续样本作为基础单元进行存储。

优先经验回放池是通过TD-error, 即目标Q值和估计Q值的差值来评判样本的价值[16-17]。TD-error越大，则该样本的优先级p越高。样本j的采样概率P(j)为：

(14)

式中：i为经验回放池中的所有样本编号；pi、pj为样本的优先级，即所计算出的TD-error值；参数α控制采样的随机性程度，取值范围为[0,1]，α=0时表示均匀采样，α=1对应于完全根据优先级的贪婪式采样。

优先经验回放增加了网络向有较大学习价值的样本进行学习的概率，从而提升学习效率，使网络更快收敛。

多步优先经验回放池如图1所示，其构建步骤如下：

1.初始化多步学习中的超参数n和一个大小为n的队列q，初始化优先经验回放池B；设置总的运行次数T和环境状态d

2.fort=1 toTdo

3. 初始化环境

4. whiled==False

5. 执行动作后，产生样本信息(s,a,r,s′,d)

6. if q 已满

7. 删除q中第一个样本，将(s,a,r,s′,d)存入q的末尾

8. else

9. 将(s,a,r,s′,d)存入q末尾，形成一个向前移动的滑动窗口

10. end if

11. 将q队列存入B中，计算TD-error：pj=R′+Qtarget-Qeval，其中R′为q队列的样本回报总和；按式(14)更新当前q队列的优先级

12.end while

13.end for

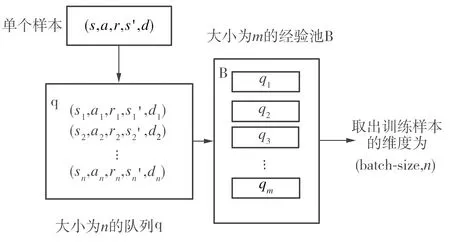
图1 多步优先经验回放池的结构

Fig.1 Structure of multi-step prioritized experience replay buffer

2.4 重抽样优选经验回放池

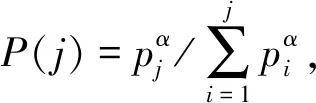
2.5 双经验回放池的设置

经过重抽样后，回放池中的记忆单元不再独立，经过若干次迭代后，具有高权重的记忆单元将被多次复制，而具有较低权重的记忆单元将逐渐消失，使回放池中的训练集太小或不充分。

为解决上述问题，使用两个经验回放池：B1和B2。B1为多步优先经验回放池，B2为单步优先经验回放池。B1无差别存储样本，B2采用重抽样机制来存储样本，以概率P(j)将样本存入B2。训练时，每局结束后网络开始迭代更新参数，样本从B1中获取。在模型已能取得较好的回报之后，改为每局中单步迭代更新参数，样本从B2中获取。通过更好的训练样本，增加迭代次数以提升网络性能。

2.6 本文算法流程

MPNTD3算法的详细步骤为：

1.用参数θ1、θ2、φ初始化估计网络中 的Critic 网络(Qθ1、Qθ2)以及Actor 网络(μφ)

3.初始化经验池B1、B2，设置游戏步数阈值stepNum、延迟更新参数f、总的运行次数T、环境状态d、学习率τ

4.fort=1 toTdo

5. 初始化环境

6. whiled==False

7. 根据a～μφ(s)+o,o～N(0,σ)选择动作

8. 执行动作后，将(s,a,r,s′,d)存入经验池B1中，通过公式(14)得出概率p，以概率p存入经验池B2

9. ift>stepNum

10. 按维度batch-size从B2中采样:(s,a,r,s′,d)

11. 按式(11)进行噪声剪切后得到a′

12. 通过式(13)得到目标值

13. 更新 Critic 网络：

14. end if

15. ift%f==0

16. 根据式(7)更新Actor网络

17. 更新目标网络参数：

θ′1←τθ1+(1-τ)θ′1

θ′2←τθ2+(1-τ)θ′2

φ′←τφ+(1-τ)φ′

18. end if

19.end while

20.从B1中采样(s,a,r,s′,d)，重复步骤11～18更新网络参数

21.end for

3 实验与结果分析

3.1 实验环境及参数设置

为了验证改进算法的有效性并分析关键参数对算法的影响，下面针对OpenAI Gym平台[18]Box2D仿真库中的Walker2d-v2场景进行研究，如图2所示。Walker2d-v2场景是为了使二维双足机器人更快更稳地向前行走。编程语言为Python 3.6.6，使用PyTorch 0.4搭建网络，其他软件包括OpenAI Gym 0.10.0、Box2D-py 2.3.8。

图2 Walker2d-v2场景

Actor和Critic网络结构的前两层均采用噪声层，分别由400和300个神经节点组成，第一层后面和第二层后面都是激活函数ReLU，Actor的网络尾部连接激活函数tanh作为最后输出。Actor第一层输入为状态s，Critic的第一层输入为状态s和动作a。所有的网络参数均采用Adam算法作为梯度下降方式，学习率为0.001。 噪声层中σ=0.4，用于初始化噪声流的权重。

目标策略平滑处理中有o～clip(N(0,σ),-c,c)，参数σ=0.2、c=0.5，延迟更新策略中参数f=2。对优先经验回放池的参数α进行优化，α分别取0.1、0.3、0.5这3个值，经测试，α为0.1和0.3时算法表现良好，其中α=0.1时表现最佳，因此后续实验均取α=0.1。计算TD-error时，为防止TD-error为0而给其加上一个极小数v，v取0.0001。总训练步数为106，经验池容量为5×105，batch-size为100，游戏步数阈值stepNum分别为4×105、6×105、8×105，经测试，在stepNum=6×105时表现最佳，多步学习策略中的n值十分敏感，在后续算法分析中比较了n分别取1、3、5、7时的训练情况。

训练时，Walker2d-v2场景由种子0～10产生10个随机的初始环境，每个任务运行106步，每5000步评估一次网络。通过TD3、NTD3(噪声网络+TD3)、MNTD3(多步截断双Q学习+噪声网络+TD3)和MPNTD3这4种算法在Walker2d-v2场景下的得分进行比较分析，其中MNTD3采用普通的经验池结构和采样机制，将普通经验池中单个样本为存储单元改为多个样本为一个存储单元，对存储单元随机采样。

3.2 结果分析

由于深度强化学习没有训练数据集和验证数据集，难以在线评估算法的训练情况。因此，训练效果的评估主要有两种方式：一是使用回报值，网络训练一定周期后，平均回报值越高表明网络训练效果越好；二是训练的网络越快达到稳定表明算法收敛性越好。

3.2.1 优化策略实施效果

首先分析噪声网络、多步截断双Q学习以及双经验回放池这3个优化策略对提高本文算法性能的效果。

图3(a)、图3(b)分别为Walker2d-v2场景下种子取0和1时4种算法的学习曲线，其中n为多步学习的步数。表1为各算法在种子取0和1时的最高回报的平均值。由图3和表1可以看出：噪声流的引入增加了网络参数的随机性，使得NTD3算法的最高回报均值比TD3算法的相应值少了53.1%，网络收敛速度也大大下降；MNTD3算法通过多步截断双Q学习策略避免了局部最优问题，虽然相比于TD3算法，其最高回报均值仍下降了近10%，但是网络收敛速度比NTD3和TD3算法都有所提高；MPNTD3算法通过考虑多步信息和提高训练样本质量，在多步参数n为3和5时，最高回报均值比TD3算法的相应值分别提高了6.5%和35.9%，网络收敛速度也都优于TD3算法。

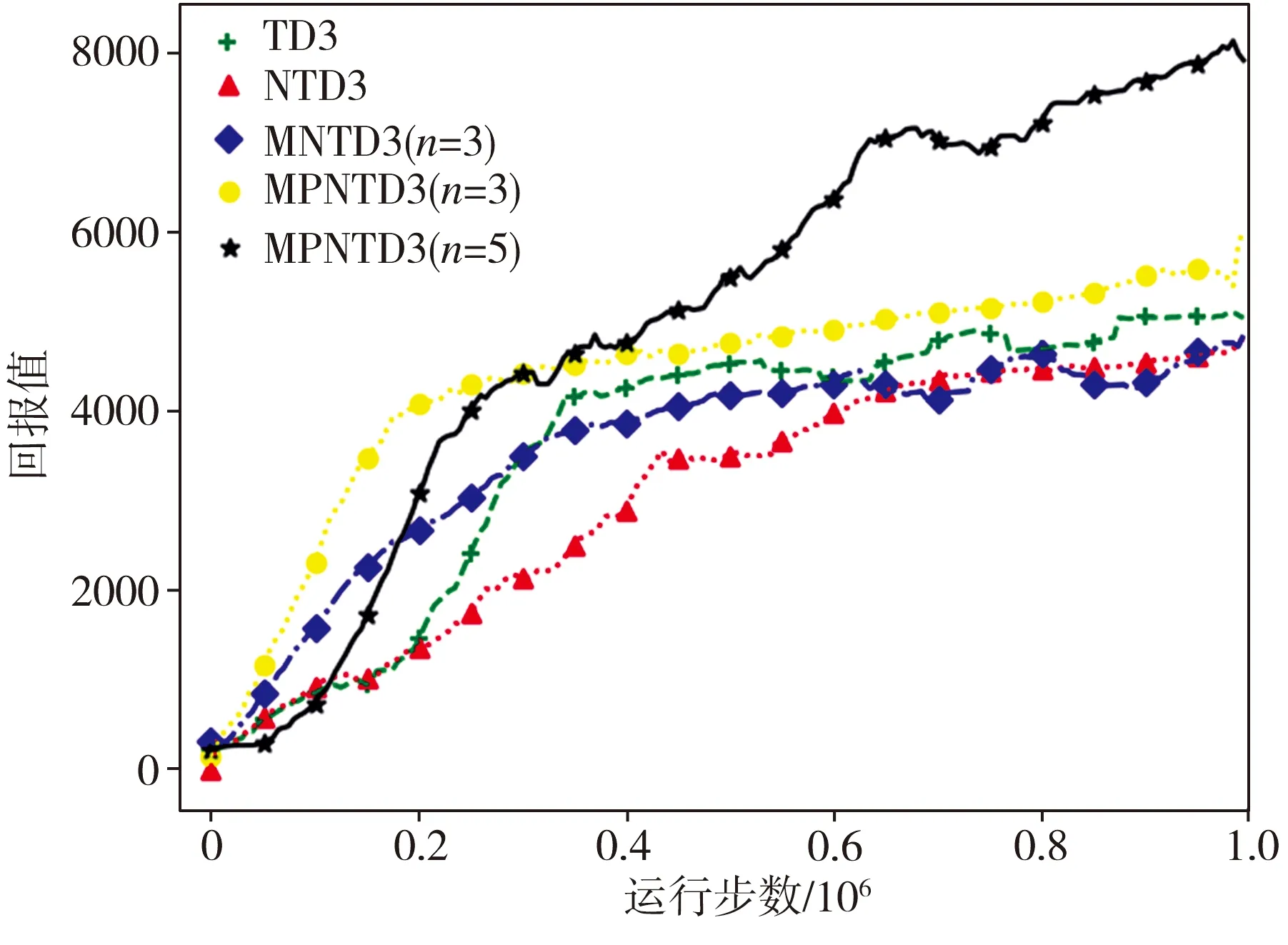
(a)种子为0

(b) 种子为1

Fig.3 Learning curves of four algorithms in different initial environments

表1 4种算法的最高回报平均值

图4为Walker2d-v2场景下种子取0时，TD3算法和多步参数n分别取1、3、5、7的MPNTD3算法的学习曲线。由图4可见， MPNTD3算法对多步学习参数n十分敏感，适当的n值使网络性能和训练速度有较大提升；在n为3和5的情况下，MPNTD3比TD3的最高回报分别提升了13.7%和60.6%；但n值过大(如n=7)会加大网络训练难度，甚至会导致网络难以收敛；在网络可以收敛的情况下，存在n值越大则前期收敛速度越慢而后期性能越好的变化趋势。

图4 TD3和取不同n值的MPNTD3的学习曲线

Fig.4 Learning curves of TD3 and MPNTD3 with differentnvalues

在Walker2d-v2场景下种子取0时，设置单优先经验回放池和双经验回放池的MPNTD3算法的最高回报分别为7996.03和8236.56。设置双经验回放池旨在选择学习价值大的样本再次训练网络，由上述结果可知，改进措施使MPNTD3算法的最高回报增加了3%。

3.2.2 算法整体性能分析

对Walker2d-v2场景中MPNTD3、TD3、DDPG算法以及Walker2d-v1场景中TD3算法(记为TD3-v1)[14]在10个随机初始环境下的学习曲线进行统计分析，结果见图5，图中曲线代表10个随机初始环境的平均回报，阴影部分代表统计指标的±σ/2区域。实验中，由种子3、4、6、7产生的初始环境下学习步数n=3，其余种子产生的初始环境下学习步数n=5。表2所示为10个随机初始环境下各算法每阶段最高回报的平均值及标准差。

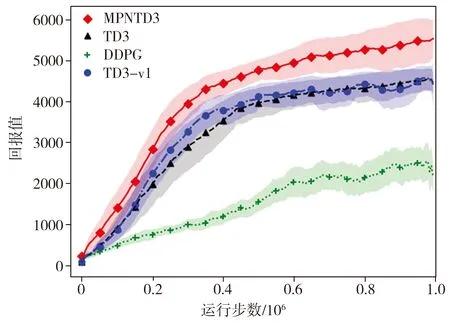
图5 不同算法在10个初始环境下的平均回报

Fig.5 Average rewards of different algorithms in ten initial environments

表2 不同算法每阶段最高回报的平均值及标准差

Table 2 Mean and standard deviation of the highest rewards of different algorithms at each stage

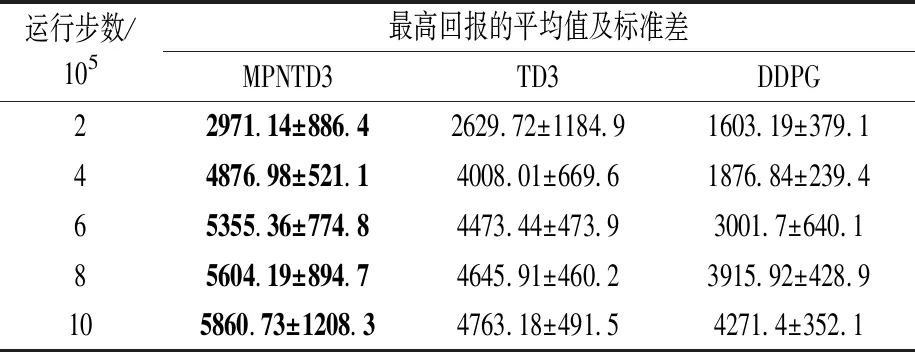
运行步数/105最高回报的平均值及标准差MPNTD3TD3DDPG22971.14±886.42629.72±1184.91603.19±379.144876.98±521.14008.01±669.61876.84±239.465355.36±774.84473.44±473.93001.7±640.185604.19±894.74645.91±460.23915.92±428.9105860.73±1208.34763.18±491.54271.4±352.1

从图5和表2可以看到，MPNTD3算法比TD3和DDPG算法的收敛速度和训练效果均有较大提升。MPNTD3算法在每个阶段的平均回报和最高回报都是最优的，而且MPNTD3在4×105步的平均回报和最高回报就超过了TD3在106步的对应值，即MPNTD3算法大大加快了网络的收敛速度。

4 结语

为了提高双延迟深度确定性策略梯度算法的网络收敛速度和探索性能，本文提出了采用双经验回放池的噪声流双延迟深度确定性策略梯度算法MPNTD3。噪声流虽然增强了策略网络的探索能力，但导致网络学习速度和训练效率都有所下降，网络更难收敛，因此通过多步截断双Q处理、考虑将来多步回报来更新当前目标值。该策略有助于算法跳出局部最优，使噪声网络变得容易收敛，但仍然存在学习能力不足的问题。而引入重抽样优选经验池和多步优先经验池后，训练样本质量得以提高，弥补了经验回放池中样本单一的缺点，加快了网络收敛速度，提升了网络训练效果。与DDPG、TD3等算法相比，MPNTD3的训练效果和训练效率均有较大程度改善，有助于解决深度确定性策略梯度算法中网络估计价值过高、探索性差、收敛速度慢等问题。