油气管道缺陷漏磁检测有限元模拟*

苏 林，成文峰，许志军，储玲玉，徐磊华，徐 杰，吉 喆

（1.中石化长输油气管道检测有限公司，江苏 徐州 221008;2.中国矿业大学 材料与物理学院，江苏 徐州221116）

管线钢管被广泛应用于石油、天然气运输，但其在使用过程中，管体及焊接接头常因出现裂纹、气孔等缺陷而造成严重的经济损失。 为了保证管道安全运输，需要定期对铁磁性材料 （管道） 进行无损检测和安全评估。 目前常用的无损检测方法有涡流检测、射线照相检测、超声检测、磁粉检测和漏磁检测法等。 其中，漏磁检测法可检测出油气管道内、外壁的金属损失缺陷，对体积型缺陷非常敏感，且不需要耦合剂，受外界干扰小，检测速度快且易实现自动化，更适于大面积、长距离管道的快速检测，是目前国内外应用最为普遍的管道内检测技术[1-5]。

本研究基于漏磁检测原理，采用ANSYS Electromagnetics 电磁场模拟软件，对管道中裂纹和气孔缺陷进行了有限元建模与计算分析，得到了两种缺陷不同尺寸下的磁通密度径向和轴向分量的分布规律，为油气管道裂纹和气孔缺陷漏磁信号特征识别提供理论基础和实践依据与参考。

1 漏磁检测原理及有限元模型

1.1 漏磁检测基本原理

管道漏磁检测器一般通过检测器励磁装置和管道本体构成磁场回路。 漏磁检测技术是建立在铁磁性材料高磁导率特性的基础上，当磁化器磁化管道时，若材料材质是均匀连续的，则材料中的磁感应线将被约束在材料中，即铁磁性的管体对磁场有聚拢作用，磁通平行于材料表面，且几乎没有磁力线从表面穿出，被检测工件表面几乎没有漏磁场[4-6]。

当材料中存在切割磁力线的缺陷时，材料表面的缺陷或组织状态变化使磁导率发生变化，由于缺陷磁导率非常小，磁阻很大，使磁路中的磁通发生畸变，磁感应线流会发生变化，除了部分磁通直接通过缺陷或通过材料内部绕过缺陷，还有部分磁通会泄露到材料表面上方，通过空气绕过缺陷再进入材料，从而在材料表面缺陷处形成漏磁场 （如图1 所示）。 利用磁敏元件可检测出该漏磁信号，从而判断缺陷的存在和特征。 利用基于麦克斯韦方程的有限元法和计算机辅助工程软件可以求解漏磁场分布情况[7-14]。

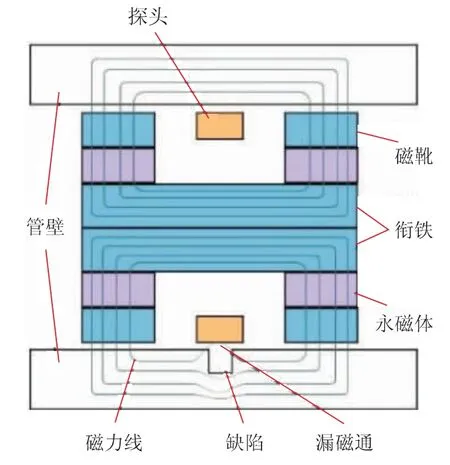
图1 管道漏磁检测原理

1.2 有限元模型

ANSYS 电磁学是以Maxwell 方程组为电磁场分析的出发点，利用有限元法来求解电磁场的一种方法。 恒定电流和永磁体激励产生的磁场属于静磁场，可以通过安培环路定理、高斯磁通定理及电磁物质的关系进行描述[15]，即

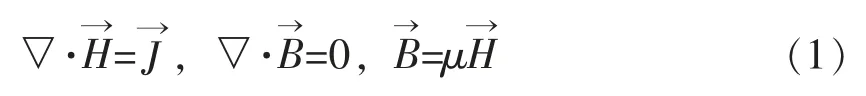
μ——介质磁导率。

由于磁场的无源性，引入矢量磁势，则有

由公式 （1） 与公式 （2） 可得

在直角坐标系中，公式 （3） 可表示为

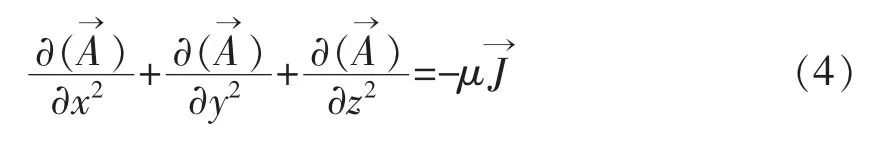
上式可通过有限元方法求解电磁场偏微分方程的近似解，在设定区域和边界条件下即可得到磁场分布。

本研究选用X60 钢级Φ529 mm×9 mm 钢管，为便于比较，研究均采用轴向励磁方法对管道缺陷漏磁场进行仿真模拟，探头提离值取1 mm。 模型中设钢管磁通密度径向分量为Bx，轴向分量为By。

对于裂纹缺陷，为简化模型并便于比较，这里考虑钢管内壁表面裂纹，宽度为0.5 mm，且沿管径环向一周，深度分别取 10%t、30%t、50%t 和 70%t （t 为钢管壁厚） 进行模拟计算。

对于气孔缺陷，这里考虑孔径（0.5 mm、1.0 mm、1.5 mm 和 2.0 mm） 和气孔中心距管道表面深度 （10%t、30%t、50%t 和 70%t） 两个变量参数进行比较分析。

2 ANSYS模拟结果与分析

为了验证有限元模拟方法的可行性和有效性，图2 分别给出了无缺陷和有缺陷时有限元模拟计算得到的磁力线分布云图。 由图2 可以看出，无缺陷时，管道经过励磁后，由于其磁导率远大于空气，因此，绝大部分磁通从管道内通过构成回路，即磁力线均匀通过管体，好像被约束在管体材料中 （见图2 （a） 中红色区域），在提离值位置提取漏磁场的磁通密度分布，结果显示其值为一磁通密度近乎为零的水平线； 有缺陷时，缺陷附近有明显的磁力线漏出管体，并且在提离值位置可以看到明显的漏磁信号 （如图2 （b） 所示），可见，模拟漏磁通是可行且有效的。

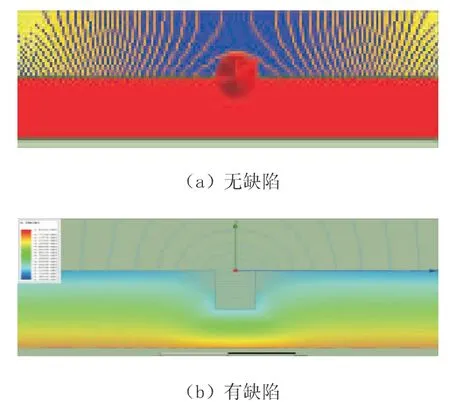
图2 有缺陷和无缺陷磁力线分布云图

在实际应用中，影响漏磁信号的因素很多，如缺陷的外形尺寸、探头的提离值、缺陷的延伸方向、管道磁化强度和材料的应力变化以及检测装置的移动速度等等，但其中对磁场影响最大的是缺陷的外形尺寸和延伸方向。 本研究主要针对裂纹和气孔两种缺陷的特征尺寸，即裂纹沿管壁厚的深度和气孔的直径以及距表面不同位置时所产生的漏磁场分布特征进行分析。

下面分别改变裂纹和气孔的特征尺寸参数，通过比较分析，可以直观地看到这两种缺陷不同尺寸下管道漏磁场的分布规律。

2.1 裂纹

图3 和图4 分别给出了不同裂纹深度 （10%t、30%t、50%t 和 70%t） 时，裂纹管缺陷处沿管径方向的磁通密度分量Bx与缺陷处沿钢管轴向方向的磁通密度分量By的分布曲线。 由图3 可以看出，Bx呈现典型的一正一负两个峰； 由图4 可以看出，By的漏磁信号则以裂纹中心呈对称分布。 当裂纹深度较小 （10%t） 时，Bx和 By的漏磁信号非常弱； 随着裂纹深度的增加，磁通密度Bx和By的峰值均呈明显的递增关系，该结果与文献 [3]报道的试验测试结果一致。 另外，By分布曲线随裂纹深度的增加逐渐变得尖锐 （如图4 所示）。

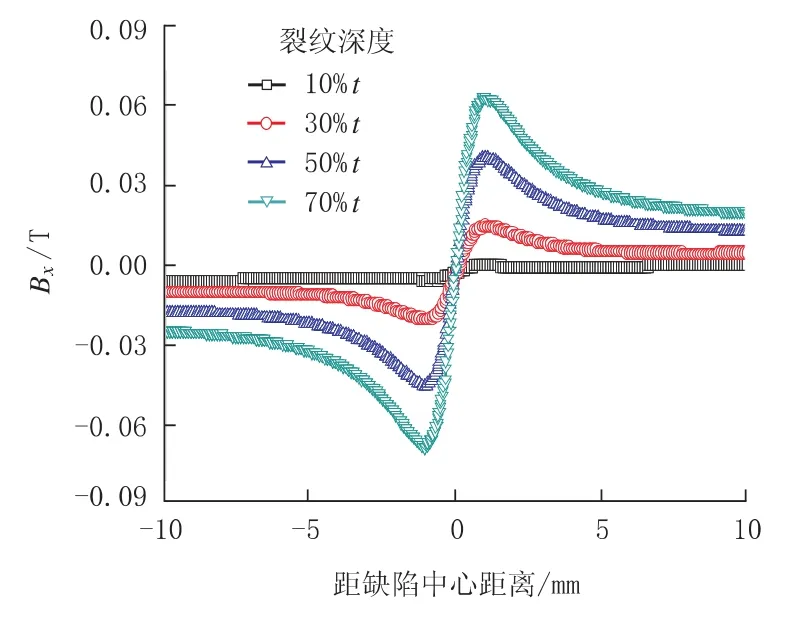
图3 不同裂纹深度时裂纹管磁通密度Bx 分布曲线

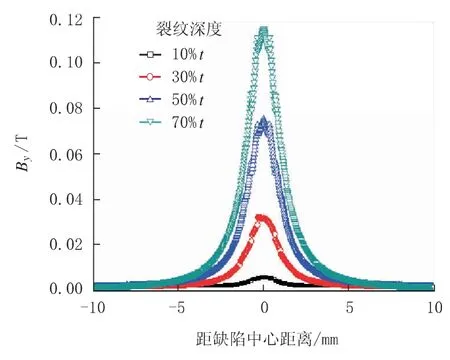
图4 不同裂纹深度时裂纹管磁通密度By 分布曲线

另外，由图3 和图4 可以看出，不同裂纹深度情况下，缺陷漏磁场径向分量磁通密度和轴向分量磁通密度的曲线形状基本相同。 图5 给出了不同深度下，裂纹管磁通密度Bx和By的峰值分布。 由图5 可以看出，随着裂纹深度的增加，漏磁场径向分量峰值和轴向分量峰值与缺陷深度呈近似线性关系，可以较好地描述缺陷深度，因此，可作为评价裂纹缺陷深度的特征量。 该结果进一步说明，缺陷处漏磁场磁通密度分布的径向分量和轴向分量的分布特征与缺陷外形参数特征存在对应关系，可通过该漏磁信号特征对缺陷外形参数进行初步判别，进而为管道缺陷实现精确量化奠定基础。

图5 不同裂纹深度时裂纹管磁通密度Bx 和By 峰值分布

2.2 气孔

2.2.1 同深度不同孔径

图6 和图7 分别给出了气孔中心距表面深度分别为 10%t、30%t、50%t 和 70%t 时，不同孔径的磁通密度径向分量Bx和轴向分量By的分布曲线。 考虑直径为2.0 mm 的气孔在距表面深度10%t （即0.9 mm 处） 时实际是不存在的（从模型设计的角度看，其几何形式更近似表面凹坑缺陷，限于篇幅，凹坑缺陷的漏磁场分析将在其他文章中探讨），因此，此处不做比较，故图6 （a） 和图7 （a） 中仅有 3 条曲线。

由图6 和图7 可以看出，随着孔径的增大，漏磁信号明显增强，即距表面相同深度下，磁通密度Bx和By的峰值均随着孔径的增加而显著增大。 径向分量Bx也呈现典型的一正一负两个峰；而By则表现出以气孔中心为对称分布的近馒头峰，且埋入管体相同深度时，随着孔径的增加，峰宽明显增大。

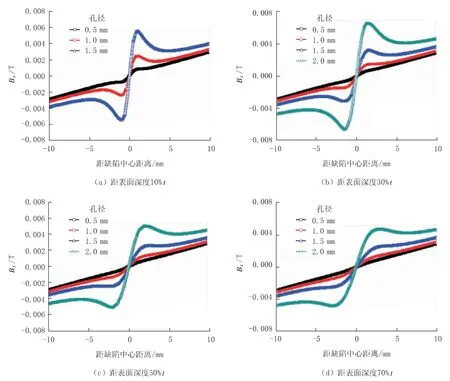
图6 气孔中心距表面深度分别为10%t、30%t、50%t 和70%t 时，不同孔径的Bx 分布曲线

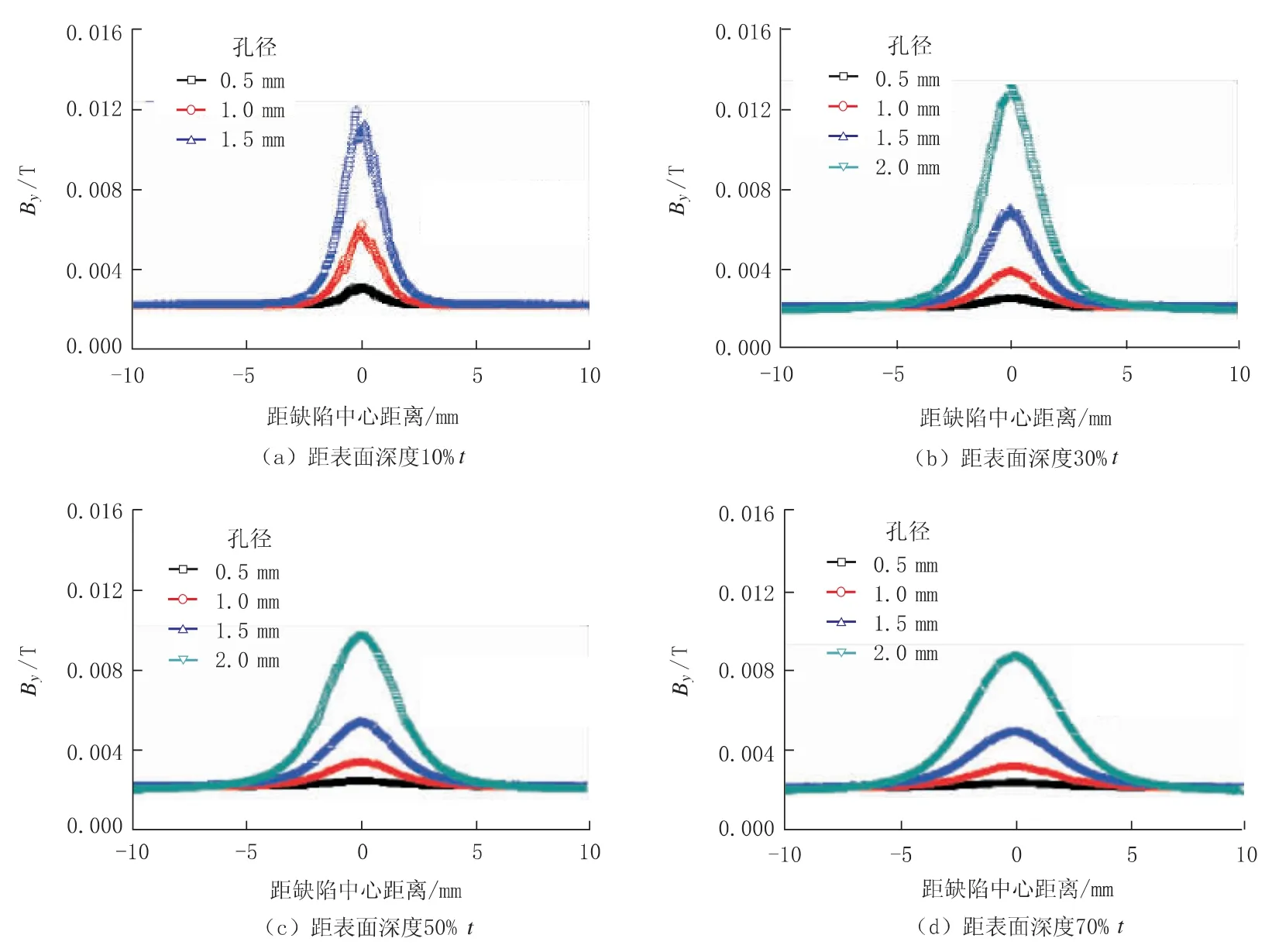
图7 气孔中心距表面深度分别为10%t、30%t、50%t 和70%t 时，不同孔径的By 分布曲线

2.2.2 同孔径不同深度

从同孔径、不同深度结果的对比进一步探讨气孔缺陷的漏磁场分布规律。 图8 和图9 给出了孔径分别为 0.5 mm、1.0 mm、1.5 mm 和 2.0 mm 时，距表面不同深度 （10%t、30%t、50%t 和 70%t） 的磁通密度径向分量Bx和轴向分量By的分布。

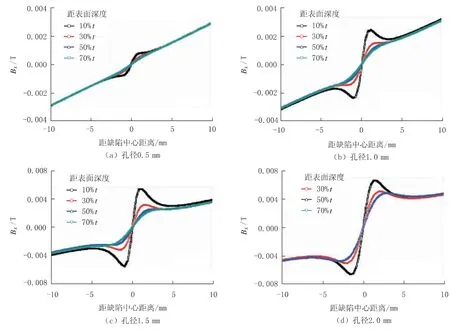
图8 孔径分别为0.5 mm、1.0 mm、1.5 mm、2.0 mm 时，距表面不同深度的Bx 分布曲线

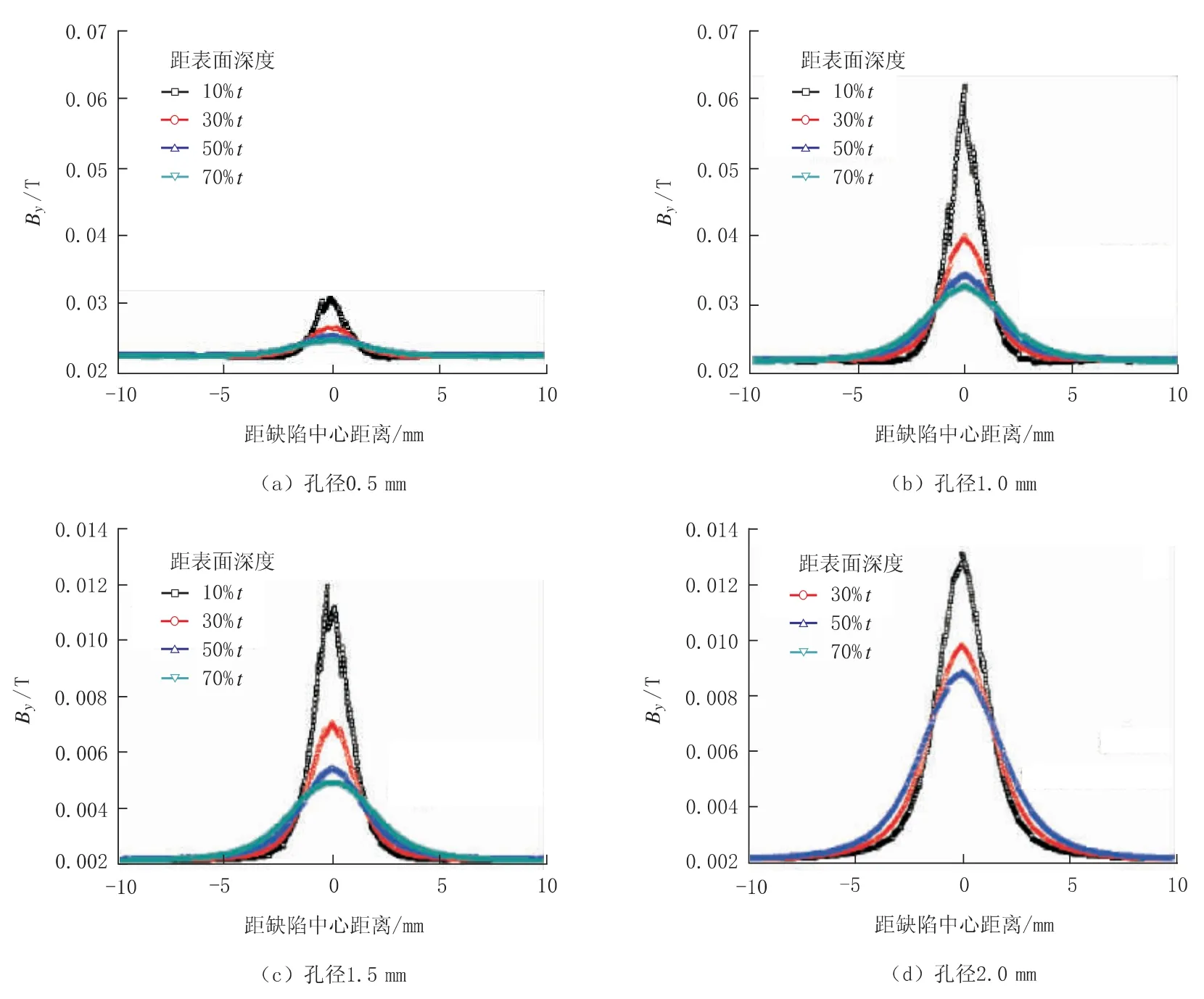
图9 孔径分别为0.5 mm、1.0 mm、1.5 mm、2.0 mm 时，距表面不同深度的By 分布曲线

由图8 和图 9 可以看出，相同孔径下，随着气孔距表面深度的增大 （即气孔埋入管体越深），气孔缺陷的漏磁信号逐渐减弱，这从计算上也可以进一步说明近表面缺陷更易于被检测。 对于较小的气孔，如孔径为 0.5 mm 时，其漏磁信号均较弱，不同埋入深度下Bx和By的峰值差别均较小 （实际检测时受检测精度的影响可能会发生漏检）。 另外，相同孔径，不同埋入深度气孔By的峰宽差别不明显，这说明埋入深度对By峰的峰宽影响较小； 当孔径较小时（如0.5 mm），不管其距表面距离大小，漏磁信号均较弱。

3 结 论

（1） 对于裂纹缺陷，随着裂纹深度的增加，磁通密度径向分量、轴向分量的峰值强度均明显增大。

（2） 对于气孔缺陷，在距表面相同深度下，磁通密度Bx和By的峰值均随气孔的孔径增加而显著增大； 相同孔径时，气孔距表面越近，漏磁信号就明显增强； 另外，By的峰宽受气孔的直径大小影响明显，而埋入管体深度对其影响较小。