移动机器人多目标搜寻的D*-蚁群融合算法

胡立坤,王帅军,吕智林,朱文天

(广西大学 电气工程学院,南宁 530004)

E-mail:w8888i@foxmail.com

1 引 言

目标搜寻是移动机器人常见任务之一,同时也是机器人领域研究的一个热点问题,通常应用于农田播种撒药、雷区探雷排雷等多个场所.根据目标数量可分为单目标和多目标搜寻问题,也就是路径规划问题和旅行商遍历问题[1](TSP)的结合.目标搜索本质上是机器人自主导航的问题,而路径规划是实现自主导航的关键技术之一[2],针对路径规划问题国内外学者做了大量研究,提出了多种算法:传统的有人工势场法[3],其最大的缺点是容易陷入局部最优导致无法找到全局最优路径,启发式算法A*和D*等由于其搜索高效性在路径规划中也得到广泛应用[4,5],随着计算机技术发展,智能优化算法也逐渐利用在路径规划上,遗传算法[6]、粒子群算法[7]和蚁群算法[8]等等,也包括了传统算法和智能算法结合[9]的方法.当目标点不只一个,此时除了路径规划问题,则还会涉及到TSP问题,TSP求解方案有精确法和近似法,在目标点较多时,精确法处理时间长,无法胜任,而智能算法作为得到近似解的最好方案,在解决TSP问题中最常用[10,11].由于蚁群算法的鲁棒性强、并行性高同时容易融合其他算法,在TSP问题以及路径规划问题和指派问题等等上有着广泛的应用前景[12].

D*算法是1994年Stentz提出的一种动态搜索算法[13],是在A*算法的基础上,通过将终点当作扩展节点的起点一直扩展到原始起点,利用反向指针沿着成本最低的路径找到一条从原始起点到原始终点的路径,D*算法的优势在于在机器人行进图中地图成本更改时,二次规划可以利用之前规划的地图信息减少计算量.针对D*算法的一些问题,文献[14]提出一种拓展Moore型元胞结构来改善路径长度,通过跳点法来找到机器人感兴趣的点,节省计算时间.文献[15]通过遍历路径中所有节点,当两个节点之间没有障碍物时,删除其中间节点并直接连接前后节点,建立平滑路径模型.上述改进一定程度上解决了原始D*算法的某些缺陷,但对于实际应用时,生成路径十分贴近障碍物的问题并没有解决,同时当搜索目标点有多个的时候,单纯的D*算法是无法解决的,此时还需要考虑一个最短遍历的问题.本文首先通过改进D*算法,解决上述问题,同时将改进D*算法融合蚁群算法来解决多目标遍历和路径规划的问题.仿真实验结果表明,本文提出的融合算法能有效完成多目标搜寻任务,同时在规划速度、转角的度数和次数、路径安全质量等一些移动机器人行走时的关键因素有明显改善,并且本文融合算法和单个蚁群算法以及蚁群算法与传统A*、D*算法融合的效果比较而言有明显优势.

2 问题描述与模型

2.1 地图环境建立

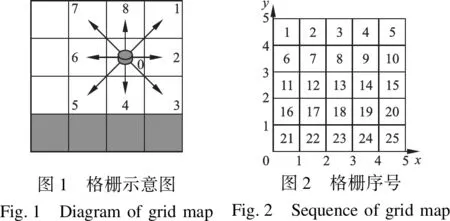
格栅法建立地图模型原理简单、容易实现,因此在地图模型的建立中得到广泛的使用,基于格栅法建立地图模型,每一个格栅对应着实际环境的某一个位置,格栅地图的分辨率是一个重要的参数,分辨率越高,环境表示越精准;分辨率越低,处理速度越快,但是会影响路径规划的精度.本文所研究的是中小范围环境,格栅法建立地图模型是合理的.

如图1所示,灰色圆柱体为机器人所在节点,箭头所指方向为节点可扩展方向,深灰色格栅为障碍物,在本文中将机器人考虑成质点,同时只涉及二维平面内的移动.图2所示为格栅序号和实际坐标的对应关系,那么机器人在格栅地图中的实际位置和地图坐标的对应关系为:

(1)

其中mod代表取余运算,ceil代表求整运算,根据式(1)就可以得到机器人在当前格栅地图中的真实坐标.将地图信息存放在二维矩阵map(i,j)中,矩阵可以表示为:

(2)

2.2 目标搜寻数学模型

该问题数学模型是一个最短路径求解问题,用集合V={v1,v2,…,vi,…,vn}表示所需要搜寻的目标点集合,vi代表所需要搜寻的第i个目标,v1代表机器人的出发点视作第一个需要搜索的目标,n代表目标点个数,最优路径目标函数为:

(3)

则现在需要做的即找到一个解向量使得式(3)最小.

2.3 两种算法描述

2.3.1 蚁群算法

蚁群算法数学模型如下:在t0时刻,将m只蚂蚁随机放置在n个目标中,初始化所有路径的信息素值,t时刻边(i,j)上的信息素表示为τij(t),t0信息素为τij(0).在后续任意一只蚂蚁移动过程中都是根据信息素浓度来决定移动方向,其选择概率为:

(4)

τij(t+1)=(1-ρ)τij(t)+Δτij

(5)

(6)

(7)

2.3.2 D*算法

D*算法是一种动态逆向搜索算法,即从目标点开始扩展直到将起点,其估价函数为:

f(n)=g(n)+h(n)

(8)

其中g(n)是基本项,代表终点(Goal)到当前节点的实际成本;h(n)为启发项,代表当前节点到起点(Start)的最小成本估计值;n为当前节点.D*算法一般采用欧氏距离作为距离计算方式,如式所示,首先需要对每个节点进行平方根运算,降低了处理速度,其次欧氏距离不考虑角度的限制,是二维或三维空间中任意两点的真实距离,而本文采用格栅法建立地图模型,对于地图中两个格栅之间的距离不能准确描述.总的来说,D*算法的搜索效率直接取决于估价函数的选取,可以根据实际环境选择不同的估价函数.

(9)

D*算法常用参数如下所示:

X,Y:机器人的状态.

b(X)=Y:从状态X到状态Y的反向指针.

c(X,Y):从Y到X的弧成本,障碍物成本为无穷大.

r(X,Y):传感器实际采集到的从Y到X的弧成本.

t(X):状态X的标签(例如OPEN、CLOSED和NEW).

h(X):实际目标点到各个格栅的最短路径成本.

k(X):当X状态发生变化后例如行进过程中原有自由空间堵塞,那么成本h(X)会发生改变,k值取变化前后最小的h值即k(X)=min(hold(X),hnew(X)).

传统D*算法计算流程如图3所示,黑色为障碍物,白色为自由空间,(2,1)为实际起点;(7,6)为实际目标点,不同与A*算法,D*算法将(7,6)作为节点扩展起点,直到将实际起点扩展到OPEN表中,通过图3中黑色反向指针找到最优路径:

图3 D*算法

3 算法改进与融合

3.1 D*算法的改进

DChess(Goal,n)=max(|xGoal-xn|,|yGoal-yn|)

(10)

加之修改后的路径成本,那么改进后的D*算法启发项为:

h(n)=10hstraight+14hdiagonal=10||yGoal-yn|-|xGoal-xn||+14min[|yGoal-yn|,|xGoal-xn|]

(11)

针对原始D*算法生成的路径小范围转角过多的问题,通过改进其启发函数得到一定程度的解决,但是效果还不够理想,同时生成路径过于靠近障碍物,对实际机器人的行进产生安全隐患,因此将子节点的扩展机制进一步改进.改进的扩展机制分为两部分:一是改进子节点代价值计算,而是子节点的扩展选取.

图4 原始扩展方式

由于原始D*算法长度优先的特性,若如图4所示的3号扩展方向的节点成本最低,那么生成的路径(浅灰色区域)就会紧靠着着障碍物,在仿真环境中是可行的,但实际应用起来往往会造成目标点不可达.

图5 子节点扩展方向

这里再将子节点的基本项进行改进,添加角度偏移产生的额外代价,那么新的基本项如式(12)所示:

gnew(n)=gold(n)+Δ(n)

(12)

Δ(n)为角度偏移代价,根据Δφ的值,定义Δ(n)为:

Δ(n)=Δφ*σ

(13)

其中,σ为角度偏移系数.

最后将图4中横竖方向节点当作一级节点(2、4、6、8),斜向节点当作二级节点(1、3、5、7),那么现在子节点扩展选取改变为:若节点2不可达,则将1、3节点也标记为不可达,因此不会生成0-1、0-3路径.其它的一级节点和二级节点选取以此类推.

3.2 两种算法融合

本文的核心是解决多目标搜寻问题,在3.1节中,已经对原始D*算法进行改进,则此时还需考虑TSP问题,若单独使用改进D*算法,找到任意两个目标点之间的最短距离,会导致路径结果不一定是全局范围中的最优路径.本文引入蚁群算法融合改进D*算法来解决该问题,蚁群算法的目标函数根据式表示为:

(14)

其中minL表示最优路径的长度,d(vi,vi+1)表示任意两个目标点之间的长度即为式中的启发因子,传统蚁群算法启发因子是根据目标点的坐标来计算,也就是Dijkstra算法,这种距离启发因子对下个节点寻找的启发性不强,尤其是当两个目标点距离较远时,存在着计算时间长、启发效果差和易陷入局部最优的缺点,如图6所示,利用蚁群算法路径规划,仿真环境为20阶,规划时间t=59.034s,若在更加精密环境例如100阶、600阶的地图矩阵中计算时间将会更久,这样的规划速度是难以接受的.因此将原有的启发因子用改进D*算法来计算,即式中分母部分采用改进D*算法来求解.

图6 蚁群算法路径规划

4 算法流程

算法融合流程如图7所示.

图7 算法融合流程

具体步骤如下:

步骤1.采用格栅图对机器人工作环境建模,建立n阶地图,同时建立一个map矩阵对格栅状态进行存储,初始化蚂蚁数量NP=80,目标数m,信息素重要权值alpha=1,启发项重要权值beta=5,最大迭代次数Maxgen=200,形成初始信息素矩阵Tau,将各代最佳路径长度存放在bestLength,各代最佳路径平均长度meanLength.

步骤2.初始化Open和Closed列表,n阶地图矩阵map(map==1)=inf,map(map==0)=1,确保起点终点不是障碍物,map(S)=0;map(T)=0,确定成本矩阵f=NaN*ones(n,n).

步骤3.如果Open表不为空,选择Open表中成本最小的格栅,将访问的格栅放入Closed表中同时更新Open表,评估领域空间中所有节点,如果节点在Closed中且成本更小,则进行更新,成本无穷大,说明是障碍物,跳过该点.若节点既不在Open表中,也不在Close表中,将其插入Open表,如果节点位于Open中,判断新路径是否更优如果节点位于Close中,判断新路径是否更优,如果更优解,则更新.

步骤4.回溯所有父节点得到距离函数D.

步骤5.将NP只蚂蚁随机放置在地图中,初始化信息素矩阵Tau,路径记录表Table=zeros(NP,m)和新的启发函数Eta=1./D,将Eta带入式建立的概率分布进行蚂蚁下一步节点选择,已访问节点放入禁忌表tabu中.

步骤6.由各个蚂蚁的路径距离计算最短路径bestLength及平均距离meanLength,伪代码如下,更新信息素dTau=zeros(m,m),进行下一次迭代,清空Table.

步骤7.循环执行步骤6直到最大迭代数或找到最优解.

步骤8.输出最优结果:

Shortest_Length=min(bestLength).

5 仿真结果与分析

为了验证算法的质量和效率,在MATLAB中进行以下仿真实验,分别采用蚁群-A*算法(ACO-A*)、蚁群-D*算法(ACO-D*)和本文提出的蚁群-改进D*算法(ACO-MD*),在地图1(100阶)中搜索5个和12个目标,在地图2(600阶)中搜索8个目标,然后分别对比其实验结果.参数初始化前所述,两份仿真地图如图8所示.

图8 矩阵地图

在100阶地图中,选取5个目标为node=[34 20;90 50;14 71;10 90;30 50],12个目标为node=[10 90;20 95;15 50;50 50;30 30;40 10;70 20;80 30;90 50;75 55;80 85;40 80].仿真结果如图9、图10所示.

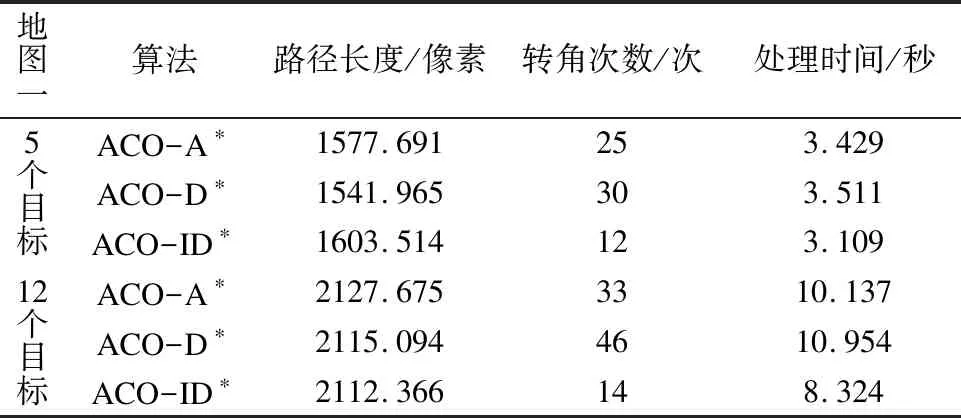
表1 实验数据对比

Table 1 Comparison of experimental data

地图一算法路径长度/像素转角次数/次处理时间/秒5个目标ACO-A∗1577.691253.429ACO-D∗1541.965303.511ACO-ID∗1603.514123.10912个目标ACO-A∗2127.6753310.137ACO-D∗2115.0944610.954ACO-ID∗2112.366148.324

从图9、图10看出,三种组合算法都能顺利完成任务,但前两种算法存在明显缺陷,首先是两种算法都太过于靠近障碍物,将地图一的标度尺寸设置为671×621像素,通过表1三种对比参数知,三种算法在路径长度上基本一致,而在转角次数上ACO-A*、ACO-D*这两种算法转角次数相比于ACO-ID*在搜索5个目标时多了13和18次、搜索12个目标时多了19和32次,若实际应用在机器人上会产生更多能耗.将ACO算法中的启发项替换为本文提出的改进D*算法,在搜索5个目标时处理时间分别为前两种算法的90.6%和88.5%,12个目标时分别为82.1%和86%,因为当前处理环境为100阶矩阵,而且是一种开放环境,无法将地图进行局部分解,所以性能有所提升但不够明显.

地图2模拟的是一个室内环境,地图阶数n为600,对障碍物的外形以及自由空间的描述会更加精细,由于室内环境边界是完全封闭的,这里利用Voronoi图[16]来得到一个离线先验路径,如图11粗黑色曲线所示.

仿真路线如图12所示,A*和D*算法基于地图成本进行计算,为追求最短路径,很多路径都是紧贴着障碍物生成,在600阶地图下障碍物轮廓更加清晰导致该情况尤为明显,因此ACO-A*和ACO-D*除了算法本身产生了很多转角,紧贴障碍物的路径也增加了相当数量的转角,由表2知ACO-MD*相较于前两种算法而言转交次数分别减少了33次、31次,地图2标度尺寸设置为1000×1000像素,在减少转角次数的基础上路径长度比前两种算法仅仅增加6.886和91.957个像素.由于将地图2的Voronoi路线图构造出来,选取距离各个目标点最近的三叉点作为临时节点,规划出连接各个节点一个无向图,这个图可以当作是一条离线先验路径如图11所示,关闭图中灰色区域节点,在ACO-MD*算法规划时使用先验路径进行预处理,算法规划时间大幅度较低,为前两种算法的65.27%和64.26%.

图9 5个目标

图10 12个目标

图11 离线先验路径

表2 实验数据对比

Table 2 Comparison of experimental data

地图二算法路径长度/像素转角次数/次处理时间/秒8个目标ACO-A∗5006.25975671.751ACO-D∗4921.18873682.358ACO-MD∗5013.14542438.465

图12 复杂地图搜索8个目标

6 结 论

本文对多目标搜寻问题提出一种有效的解决方案,针对原始D*算法和原始蚁群算法在解决路径规划问题和TSP问题上均有缺陷,通过估计函数、子节点扩展机制等来改良D*算法路径规划能力,然后通过改进D*算法来计算蚁群算法中的启发因子.仿真实验得出,改进D*融合蚁群算法在多目标搜寻中相比于单个或其他融合算法有明显优势,证明该算法的有效性和实用性.