露天矿山爆破信号时频特征提取与分析

王 陀，林梦吟，曾艺婷，顾 城，秦 明，付晓强

（1.三明学院 建筑工程学院，福建 三明 365004；2.工程材料与结构加固福建省高等学校重点实验室，福建 三明 365004）

随着国民经济的发展和对能源需求量的增加，大型露天矿山剥离和开采规模也越来越大，露天煤矿采用钻爆法进行土石方剥离过程中产生的强振是爆破最主要的潜在危害之一[1-3]。由于爆破导致近区的建筑物开裂、边坡滑移失稳等工程现象时有发生，对安全生产带来很大威胁，对爆破产生的振动效应的研究已成为工程技术人员和科研工作者的关注热点。但现有爆破规范中并未考虑信号能量分布的影响，使得对安全标准的控制存在一定的盲目性。

本文利用山西某露天矿爆破监测数据，采用短时傅里叶变换分析对不同高程处信号进行时频分析，获得了信号能量在时频平面上的分布特征。利用非线性回归得到了信号能量衰减规律，说明了能量分布对信号信息特征描述的重要意义，探讨了将能量纳入安全规范的必要性。

1 测点布置与信号采集

1.1 测点布置

山西灵石某露天煤矿采用钻爆法进行土石方剥离，该矿区岩石以中风化石灰岩为主，爆破区域边界较为规整，共布置五排炮孔，采用潜孔钻机钻孔，使用多孔粒状铵油炸药和毫秒延期导爆管雷管起爆。此次爆破共一个台阶，起爆一次完成，其中一、二排炮孔深度为6 m,三、四排炮孔深度为8 m，第五排炮孔深10 m，孔径均为120 mm，炮孔间距为6 m,排距为4 m。爆破网路设计为双回路，孔内采用MS9段，孔外排与排间采用MS3段毫秒导爆管雷管，炮孔非装药段使用凿孔产生的岩粉封堵。爆破炮眼总数为140个，一、二排装药量为30 kg/孔，三、四排为50 kg/孔，第五排为70 kg/孔，单排单段最大装药量为1 960 kg，该次爆破共使用炸药6.5 t。爆破区域炮孔布置和测点布置如图1所示。

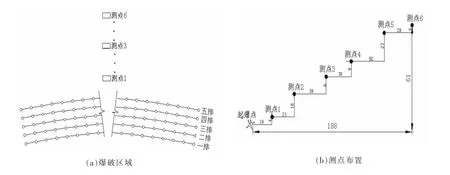
图1 爆区分布与测点布置（单位：m）

为了准确把握和客观评价大药量爆破产生的振动效应，采用6台爆破测振仪对起爆过程进行了监测。测试选用四川拓普测控生产的UBOX-5016型测振仪，测试时设定测振仪采样频率10 kHz，采样时长2 s。测点沿纵深不同高度布置在台阶面上，多个测点沿线性布置。1#测点距起爆中心的水平距离为19 m，垂向距离为4 m；2#测点水平距离为42 m，垂向距离为20 m；3#测点水平距离为80 m，垂向距离为26m；4#测点水平距离为110 m，垂向距离为34 m；5#测点水平距离为160 m，垂向距离为57 m；6#测点水平距离为180 m，垂向距离为61 m。该露天矿开挖台阶测点的具体布置和概况见图 1（b）与图 2（a）。

图2 矿区概貌和测点布置

1.2 信号采集

UBOX-5016型测振仪可同时记录水平径向、切向和垂向三个正交方向的振动信息[4-6]。测振探头布置时，选择平整的完整岩石，将岩面清理干净后，采用拌至浆状的细石膏粉将探头粘结固定，同时做好仪器的防护工作，防止爆破飞石对仪器导线的破坏和采集信号的干扰，测试后及时将仪器回收并将信号传输至电脑储存。

起爆后现场布置的6台测振仪均准确记录到该次爆破所引起的不同爆心距处的振动信息，通过对比发现三向振速主振频率较为接近，振幅具有显著差异，大体呈现竖直垂向＞水平径向＞水平切向，因此选取垂向信号进行分析更具代表性。各测点垂向信号时程曲线如图3所示。

从图中可知在爆破近区信号振动幅值较大且在时间轴上聚集程度较高，随着爆心距的增加，信号波动特征更为清晰且幅值逐渐降低，信号中包含的高频成分经过岩土介质的过滤作用大幅衰减。对测点水平和垂直距离进行折算并提取各测点信号特征信息如表1所示。

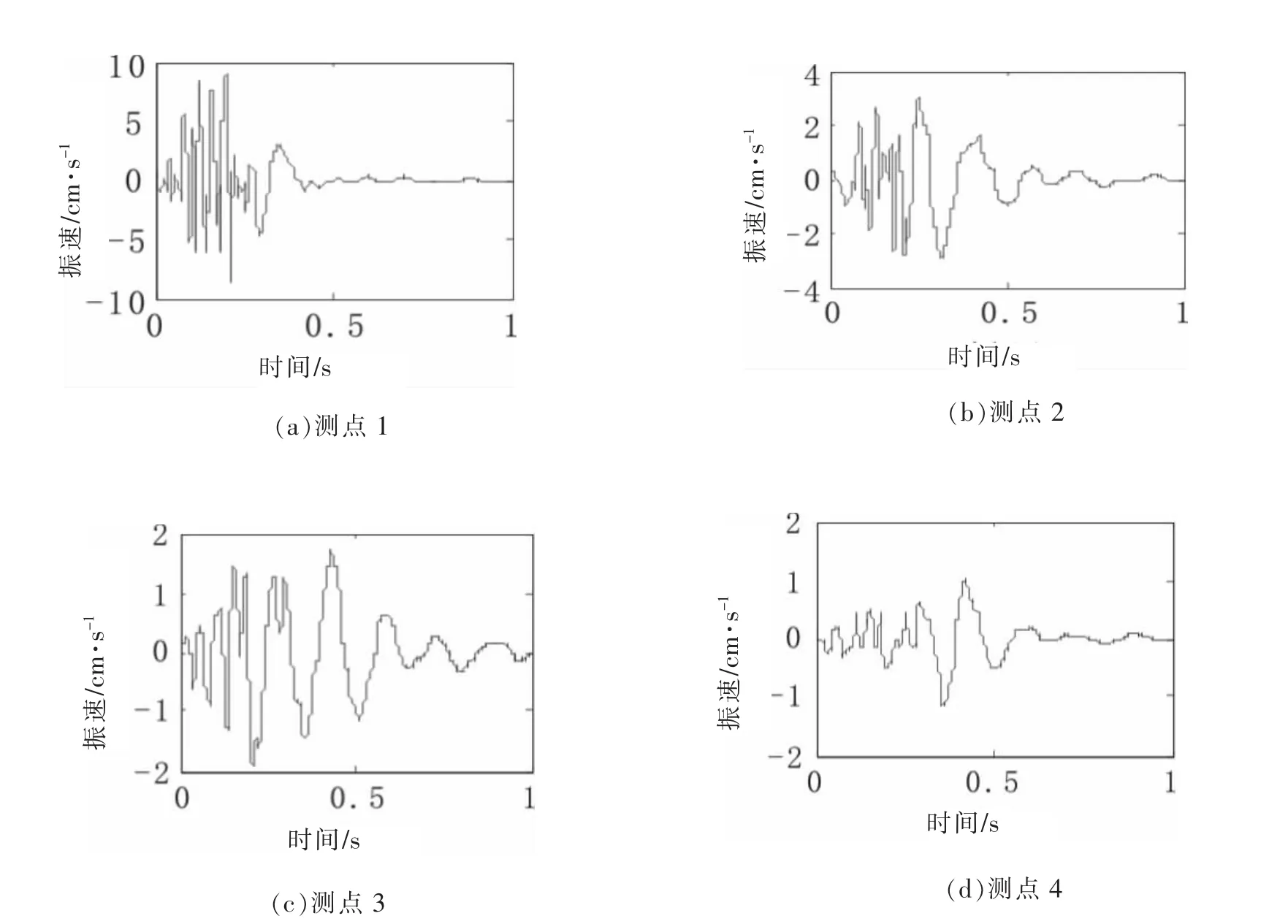
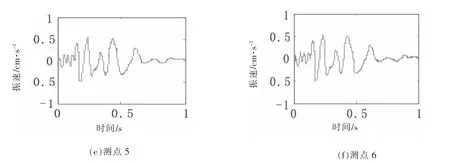
图3 各测点爆破波形曲线

从表1中可以看出该地质条件下爆破振动信号主频位于0～30 Hz范围内，随着高程和爆心距的增加，信号振幅降低且主振频带往低频发展，各测点振速的波峰和波谷幅值较为接近，且峰值时刻出现在最大段装药量的第五排炮孔起爆时刻，证明了测试数据的有效性。

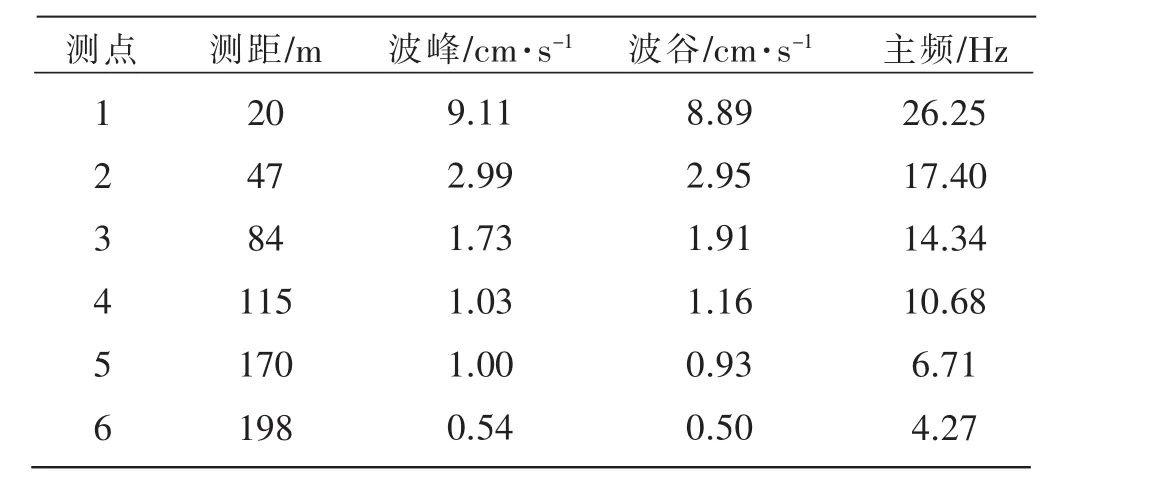
表1 各测点信息

2 STFT基本理论

为了准确提取爆破信号中包含的时频特征信息，这里采用短时傅里叶变换 （short-time fourier transform,STFT）对信号进行分析。对于任一给定的信号x（u）∈L2其短时傅里叶变换可表述为：

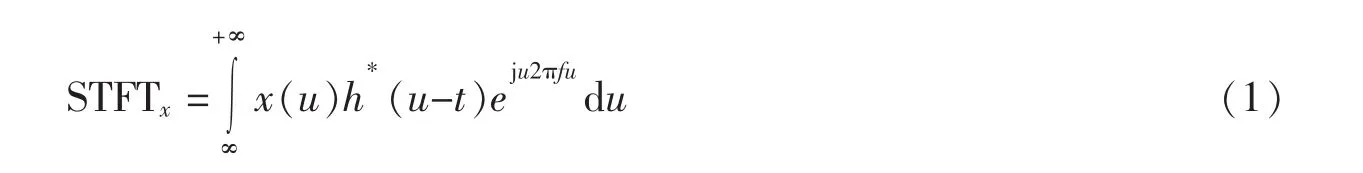
式中，h(u-t)为选取的窗函数，t为时间平移参数；*表示卷积共轭运算。通过窗函数可将信号截分为等长或不等长的多段子信号，截取到的信号可表示为：

式中，Xt为原始信号对应固定t时间点区间的信号，X（τ）为执行时间对应τ的信号。对Xt作傅里叶变换，可获得Xt的频谱，其表达式为[7]

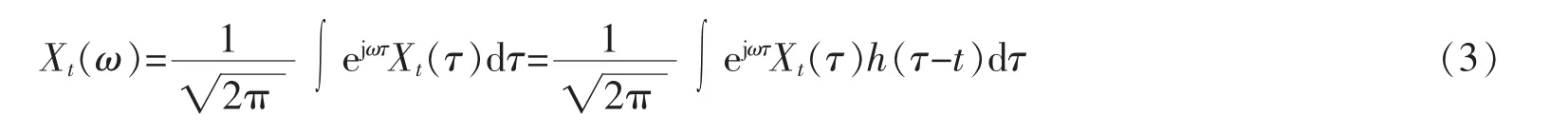
窗函数的中心位置调整可通过平移参数t的改变而实现，将不同时间间隔得到的频谱进行总和，便得到了信号的频谱图。

短时傅里叶变换谱可定义为信号短时傅里叶变换模值的平方，其频谱能量关系可表示为

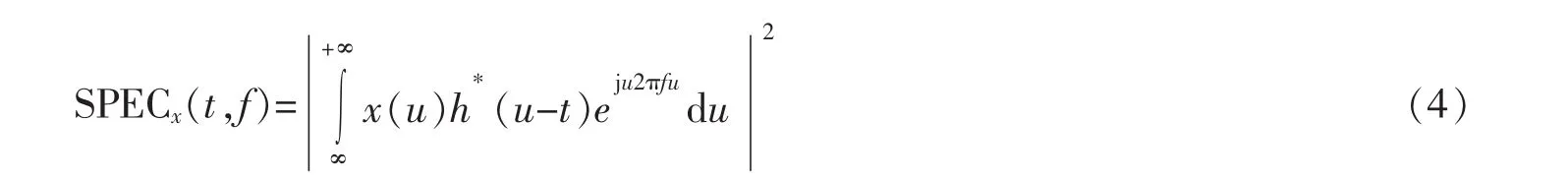
短时傅里叶变换可清晰展现信号在时域和频域局部细节，从而揭示信号能量在时频域的分布特征。

3 爆破信号STFT谱实现

爆破信号STFT谱求解时，窗函数选取对分析结果影响显著，常用窗函数包括矩形窗、汉宁窗和高斯窗等[8-10]。这里选用汉宁窗作为窗函数，确定窗长为32，步长为64，求取各信号STFT能量谱如图4所示。

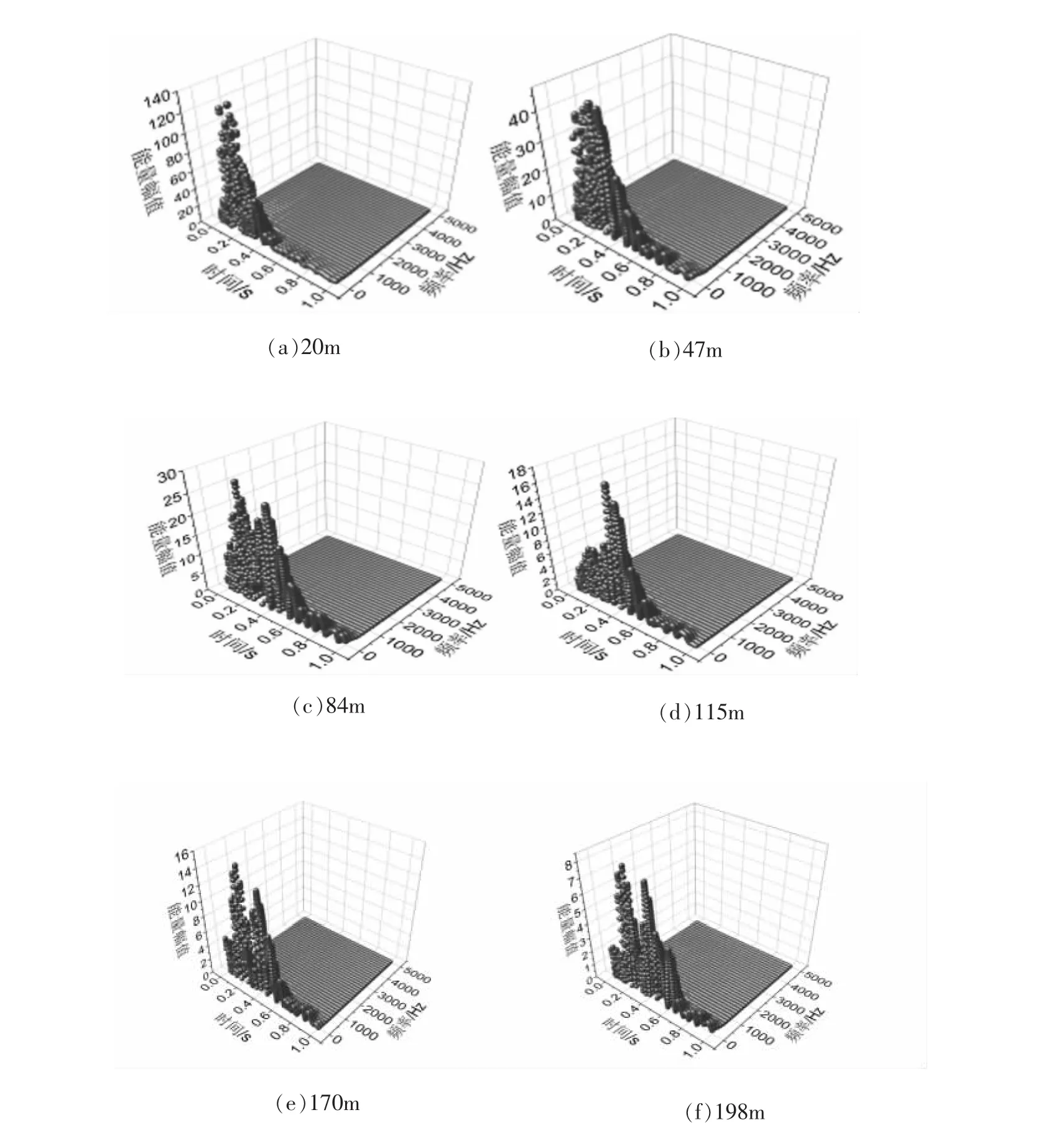
图4 不同爆心距STFT变换能量谱

不同爆心距处监测爆破信号在时频平面上的分布形态具有显著差异，能量在主频附近频带的聚集程度更高，说明爆破能量主要集中在主频段附近频带[11-12]。在爆破近区（＜20 m），信号在时频平面聚集程度较高，主要聚集在0～0.4 s和0～300 Hz时频范围内，能量幅值较高且峰值单一，具有爆破信号能量瞬态冲击特征；在爆破中区（20～115 m），随着爆心距的增大，信号能量在时频空间的分布逐渐趋于均匀，主要聚集在0～0.6 s和0～200 Hz时频范围内，在时间上的响应范围加大，边坡岩体的高程效应更多地体现在信号在时间轴上的响应增强作用；在爆破远区（＞115 m），随着爆心距的进一步增大，信号能量出现多频带、多峰值的特点，能量主要聚集在0～0.7 s和0～150 Hz时频范围内，频率范围逐渐缩小，能量分布更为广泛且分布形态逐渐稳定。

为了准确获取能量随爆心距的衰减规律，借鉴萨道夫斯基经验公式，拟合得到能量衰减公式为

式中场地系数k=234.5,a=1.61,属于中硬岩范畴。这与现场弱风化石灰岩（普式系数f=6～8）条件相一致。公式(5)说明露天台阶爆破能量随爆心距的变化呈指数衰减，且在爆破近区能量衰减较远区更为明显。说明要加强爆破近区的振动控制，测试时也应缩小近区测点间距，从而科学了解振动衰减特征，有效控制振动灾害。

3 结论

（1）对于大药量露天土石方剥离时，采用孔内高段别MS9段，排间低段别MS3段毫秒微差雷管爆破网络，现场应用收到了良好的效果，适合在类似工程中推广应用。

（2）露天台阶爆破的高程效应更多地体现在增加对爆破振动响应时间和降低振动主频两方面，在现场实践过程中，除考虑振动幅值的变化外，应结合信号时频能量谱，关注不同台阶高度处振动主频和持续时间差异，综合考虑三参量的变化从而达到调整装药参数和优化爆破网络的目的。

（3）该场地条件下，露天台阶爆破能量随爆心距的变化呈指数衰减，且在爆破近区能量衰减较远区更为明显，随着爆心距的增大，信号能量谱在爆破远区呈现多频带、多峰值的特征。在爆破振动标准制定时，应将能量特征作为安全控制标准的重要参数，从而更准确描述爆破振动的损伤效应。