云计算下一种聚合流的有效带宽接纳控制方法
余 建 ,杨晓冬 ,刘孙发 (1.三明学院 网络中心, 福建 三明,65004;
2.物联网应用福建省高校工程研究中心,福建 三明,365004;3.三明学院 图书馆,福建 三明,365004)
随着计算机网络技术的发展,云计算[1]在快速为用户提供资源的同时,还需具备可靠性、可用性、可扩展等完备的服务质量(QoS)保证机制,确保系统执行的高效性[2-3]。近年来,云服务的数量与种类呈爆炸式增长,网络流量也不断增加,导致网络负载较大。用户对QoS的要求也越来越高,传统的单流接纳控制已经不能满足用户需求。作为一种有效的预防性流量控制手段,接纳控制[4-6]是避免网络拥塞、保障云服务质量的有效方法之一。
在云计算网络中,接纳控制作为网络流量拥塞控制和服务质量保障的有效手段,得到了越来越多专家学者的关注。文献[7]中提出了一种基于负载传递的联合接纳控制算法,用户申请接入时,引入动态负载流量传输,通过建立异构网络的QoS性能指标,以此限制用户流量。文献[8]提出了一种呼叫接纳控制(call admission control,CAC)算法,联合带宽系数权重以及带宽降级策略,利用呼叫接纳控制对已接入呼叫中权重系数最小的用户进行带宽限制,再根据切换和新到达呼叫的优先级,来分配相应的带宽资源。文献[9]中通过在LTE系统中提出一种基于排队机制的动态资源预留算法,通过设置一定的阀值资源,以新呼叫的形式定义请求接入,在无可用资源的情况下,对其他资源以排队方法等待接入。目前在无线网络中使用较多的是呼叫接纳控制,其在保障接入用户的通信质量、降低系统阻塞率、控制传输速率等许多方面都扮演着关键角色。马尔可夫决策过程是解决无线通信中决策问题的一种有效方法[10],在接纳控制策略的研究中起重要作用。云计算在提供服务能力和服务资源满足用户应用需求的同时,还需要具备可靠性、可用性、可扩展性等完备的QoS保证机制,确保其系统执行的高效性。接纳控制技术是保障其系统高速有效运行的重要部分,也是云计算的前提保障。
聚合流[11]可以理解成无数网络依次到达,叠加组成的流量。聚合网络流量由多个网络用户数据源组成,在每个网络用户数据源的内部,数据的流动都有其行为模式,数据包间的到达间隔同样也遵循一定的到达规律。将所有用户数据源的数据包叠加后,便是聚合流。
1 聚合流的有效带宽接纳控制模型
云计算虽说是以传统网络为基础,但其接纳控制模型却不同于传统网络[12]。云计算中的接纳控制必须满足在保证QoS的前提下,不影响其他服务运行,考虑到云计算服务请求的高并发性,在多个请求在整形器的作用下进入到等待区后形成聚合流,然后通过接纳控制模块从入口节点进入到云服务中。由于传统的单流接纳控制方法只能同时处理一个请求,当多个单流同时进入到入口节点后,等待处理的时延加大,用户体验效果不佳。为了提升网络并发处理能力,提升云服务的QoS,本文提出了一种基于聚合流的接纳控制算法,该算法通过估计聚合流所需的带宽来执行接纳控制,能同时处理多个服务请求,云计算环境下的接纳控制模型如图1所示。
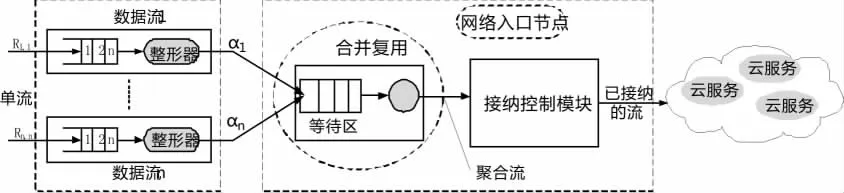
图1 聚合流的有效带宽接纳控制模型
在图1中,用户请求云计算服务的异构流经过整形器整形后,再通过FIFO复用模块调用,接纳控制模块将对复用模块输出的聚合流执行接纳控制,异构流合并复用时会进入到等待区,在网络入口节点流量一定时,能同时处理多个业务请求。
2 聚合流的有效带宽模式
2.1 网络聚合流
给定一个有向图B=(V,E),在V中指定两点,其中一点称为发点(记为v1),另一点称为收点(记为vn,n是B的顶点个数),其余的点v2,v3,…,vn-1称为中间点。对于每一个(vi,vj)∈E对应有一个cij(cij≥0),称为弧的容量。把这样的B叫作一个网络,记为B=(V,E,C)。弧集合E上的一个函数f={f(vi,vj)},称为网络上的流,并称f(vi,vj)为弧(vi,vj)上的流量,简记为aij。由文献[13-14]可知,满足下面条件的流f称为可行流。
(1)容量限制条件。 对每一弧(vi,vj)∈E,满足 0≤aij≤cij。
(2)对于中间点。流出量与流入量相等,即对于个i(1<i<n),有Σaik-Σaji=0;对于发点Σa1k-对于收点Σank-Σajn=-v(f)。
最大流问题就是求解流{aij},使其流量v(f)达到最大,且满足

2.2 聚合流的等效容量
代数法求解[15]EBAF就是利用有效带宽的定义式直接求解。利用代数法得到EBAF模型,需要引入数学中关于上确界的知识,如下
定义1设S是R中的一个数集,对于η有以下两条
①对一切x∈S,有x≤n,即η是数集S的上界;
②对任意ε>0,存在x0∈S使得x0>η-ε(η是数集S的最小上界),则称η为数集S的上确界。记为 η=supS。
定理1对于一个在定义域[x1,xn]内连续的函数f(x),若它存在上确界,那么它的上确界等于函数 f(x)各个分区间[x1,x2],[x2,x3],…,[xn-1,xn]上的上确界的最大值,即

根据定理1的内容,可以得到如下推论。
推论1对于一个在定义域[x1,xn]内连续的分段函数f(x),若它存在上确界,并且f(x)各个分区间[x1,x2],[x2,x3],…,[xn-1,xn]上对应的函数解析式为 fi(x)=(i=1,2,…,n-1)。 如果 f(x)在区间[xi,xi+1]上单调,那么函数f(x)在定义域内的上确界为


其中α*是聚合流的到达曲线,s为通过的节点,D为所有流的时延约束,聚合流的有效带宽为eD。其流量模型满足流量规范T-SPEC(pi,Mi,pi,ri),在计算过程中,且(4)就是通过代数法得到的EBAF的值。
2.3 效流量与等效容量的关系
有效带宽是从云服务的角度定义的,而等效容量是从网络的角度定义的。为了在保证云服务时延的同时,优化网络对资源(如等待区大小)的分配,需要分析有效带宽与等效容量之间的关系。根据定理1与推理1,可以得到下面的定义及定理。
定义2时延影响因子(delay impact factor,DIF)。对于到达曲线为α的流,通过一个节点S,给定流的时延约束为D,当节点的等待区大小B满足B=h(D)时,流的有效带宽等于其等效容量,把h(D)称为流的时延影响因子。 其中 h(D)=supS≥0{a(S)-eDa(S)},eD(a)流的有效带宽。
定义 3等待区影响因子(buffer impact factor,BIF)。对于到达曲线为α的流,通过一个节点S。节点的等待区大小约束为B,如果流的时延D满足D=g(B)时,流的等效容量等于其有效带宽,把g(B)称为节点等待区影响因子。 其中 g(B)=supS≥0{inf{T≥0:a(S)≤fB(a)(S+T)}},fB(a)为流的等效容量。
定理2对于到达曲线为α的流,通过一个节点S。
①如果给定时延约束D,当节点等待区的大小B满足B=h(D),此时流的有效带宽与其等效容量相等。
②如果给定等待区大小约束为B,那么只要这个流的时延约束满足D=g(B),此时,流的等效容量等于其有效带宽。
如果给定时延约束 D,本定理所表示的内容用数字表达式表示为 eD(a)B=h(D)=fB(a), 节点为流提供的服务速率为 eD(a),在 B=h(D)时,流的等效容量为
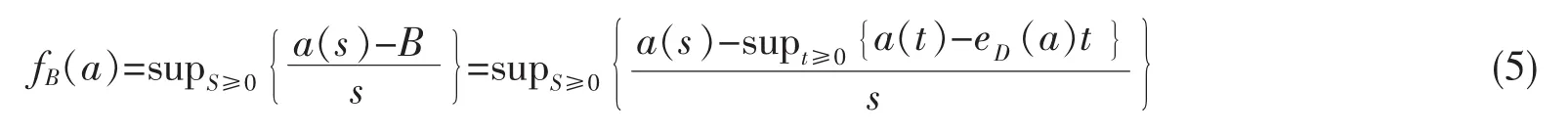
又由于
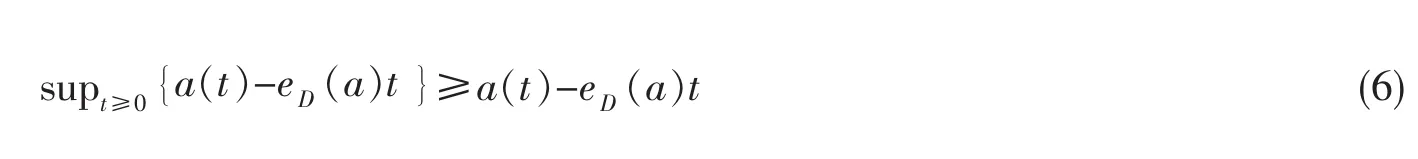
根据不等式(6)

可以看出,在上述过程中,函数值都是在定义域内进行放大或缩小,所以函数在定义域[0,+∞)内的最大值就是 eD(a),且 eD(a)也是该函数的上确界。因此,根据不等式(7),可以得到 fB(a)=eD(a)。
如果给定等待区大小约束B,节点需要为流提供的服务速率为fB(a)。定理2所表示的内容用数学表达式表示为 feD(a)B=h(D)=eD(a)。 在 D=g(B)时,流的有效带宽为

因此,根据式(10),可以得到 eD(a)=fB(a)。
有效带宽是表示在满足时延约束D时节点需要为流提供的服务速率,因此,现在考虑云服务的时延约束为D,则就是节点eD(a)分配给流的最小带宽,那么,在满足此时延约束D时,节点需要提供给云服务的最小等待区Bmin必须满足如下条件
①保证QoS不变。也就是在节点等待区大小为Bmin时,云服务通过此节点产生的时延在要求的时延约束范围内,即不能超过D;
②不能改变节点的接纳能力。也就是在等待区大小为Bmin时,在满足时延约束D的条件下,等待区不能有溢出。否则节点所能接纳的云服务数量将少于在单独满足时延约束节点所能接纳的数量。
由于时延约束D与等待区大小约束B都能影响节点接纳云服务的数量,而接纳云服务数量的多少由有效带宽和等效容量决定。若只考虑给定时延约束D时,节点接纳的云服务数量为nD,只考虑等待区大小约束B时,节点接纳的云服务数量为nB,而同时考虑两者的情况下,节点接纳的云服务数量为 n=min(nD,nB)。 因此,如果要满足第②点的条件,就必须使 fB(a)≤eD(a),而 fB(a)的值随着 B的减小而增大,那么满足条件的最小值 Bmin即是 fB(a)=eD(a)时求解得到的值。 而当 fB(a)=eD(a)时,第①点的条件显然满足。那么当给定云服务的时延约束为D,节点提供给云服务的服务曲线为β(t)=eD(a)t时,根据定理2可以得到满足条件的最小等待区大小Bmin就是DIF,且为

综合以上,对于假设云计算环境中有I种类型的云服务的场景,每个云服务的业务流的时延约束为D,结合推论1,可以推导出节点需要为I种类型流的聚合流提供的最小等待区大小Bmin为

3 基于聚合流的有效带宽接纳控制算法
当用户请求服务时,接纳控制算法根据服务参数和用户的QoS要求估计聚合流所需要的带宽,最后根据对聚合流的带宽估计和节点的带宽情况来执行接纳决策。表1给出了EBAF算法中的常用标记及含义。表2详细介绍了基于聚合流的有效带宽的接纳控制算法的执行过程,该过程主要包括以下步骤(1)第 1~10行,求出,并将从小到大排序,在此过程须保持与,的对应关系不变。(2)第11~20行,利用输入的服务参数和用户的QoS参数估计聚合流所需的带宽。(3)第21~25行,接纳决策过程。利用上一步计算得到的聚合流的带宽估计与节点带宽,判断该流的请求接纳与否。

表1 EBAF算法常用标记及含义

表2 EBAF算法
4 实验分析
本文通过计算机仿真,在CloudSim仿真器中搭建实验环境,云服务中含有2个计算节点,节点配置为:100个CPU,256 GB内存,100 TB硬盘存储,2 GB的网络带宽流量。假设每个单流到达等待区都符合马尔可夫链[16]。仿真参数我们参照文献[17],具体如表3所示。

表3 三种云服务的仿真参数
表3中参数i=4的服务流的有效带宽与等效容量如图2~3所示。从图中可以看出,随着时延约束或等待区大小约束的增大,有效带宽或等效容量会随之减小,也就是网络入口节点需要为服务流提供的服务速率变小,但最小的速率不能低于流的平均速率r,这个速率也是在满足当前约束等待区没有溢出时节点需要提供的最小速率。

图2 有效带宽图

图3 等效容量
针对EBAF算法,接纳服务流的数量都是随着时延约束D的增大而增大,这是因为随着时延约束D的增大,流所需带宽资源变少,即有效带宽变小,接纳容量增大,即时延约束越大,节点的接纳能力增加。但当时延约束增大一定程度后,不管D如何变化,接纳的数量都将保持不变。这是因为时延约束增大到一定程度后,流的有效带宽等于流的平均速率r,之后D再增大,有效带宽的值将不再发生变化,接纳服务的数量也不再变化。图5~6分别为i=1,2和i=2,3时的性能比较。通过对比我们可以得知,随着时延约束D的增大,聚合流的有效带宽比单流的有效带宽先达到最小值。

图4 i=1,2的有效带宽性能比较

图5 i=2,3的有效带宽性能比较
5 结语
为了提高云计算下网络流量的执行效率,本文提出了一种基于聚合流的有效带宽(EBAF)接纳控制算法,通过估计聚合流所需的带宽来执行接纳控制,能同时处理多个服务请求。在不同云服务参数下进行模拟仿真。仿真结果表明,本文提出的有效带宽接纳控制方法,能有效的解决云计算环境下的带宽流量控制,实现网络的负载均衡,从而提升网络并发处理的能力,以进一步提高云计算的QoS。

