采用FLAC3D的互层土基坑突涌破坏判断方法

熊宗海 ，李腾龙 ，范卫琴 ，2，袁光明 ，蔡兵华

（1.武汉丰达地质工程有限公司，湖北 武汉 430074；2.三明学院 建筑工程学院，福建 三明 365004；3.武汉市市政集团隧道工程公司，湖北 武汉430074）

数值分析方法由于其便利性被广泛用于基坑突涌稳定方面的研究，分析时只要选择合适的土层和支护结构模型、土层接触面及相关参数就能模拟实际工程中的土体及支护结构的变形特征，同时还可以追踪突涌破坏的发展过程。而准确判断基坑是否发生突涌破坏是整个数值分析的重点。针对这一问题，不同的学者采用了不同的简化及假设，提出了如下4种判断标准：（1）坑底表面土体中出现拉应力[1-3]；（2）土体内部产生铅直面的剪切破坏[4-5]；（3）坑底隆起变形突变[6-8]；（4）塑性破坏区贯穿隔水层[9]。即当计算过程中出现上述四种情况之一时，基坑发生突涌破坏。

上述方法中，第（1）种方法与国内一些室内试验[10]及现场监测[11]结果不符。而孙玉永[12]发现隔水层内屈服区域分布并不呈铅直面，而是以一定角度向中部发展，这表明第（2）种判定方法存在缺陷。第（3）种判定方法相对模糊——主要由于坑底隆起变形各阶段之间临界点并不明确，且需要做多组模拟实验才能得到承压水头与坑底隆起关系曲线，从而得到发生突涌的临界水头，因此难以确定准确的突涌破坏的发生，在数值模拟中运用有较大的局限性。第（4）种判定方法是从土体各单元的应力状态及屈服准则来判断土体是否发生塑性滑动及发生破坏。

本文用FLAC3D（美国ITASCA公司V5.0版本）模拟互层土基坑中坑底突涌的发展过程，验证第（4）种判定方法的合理性。

1 模型建立

2.1 模型尺寸

模拟在互层土地区不采用降水措施直接开挖基坑的土体突涌过程，数值模型如图1所示。其计算尺寸为长（x方向）60 m、宽（y方向）一个单位长度，即为1 m、高（z方向）20 m。最下部细砂层厚9.0 m；上覆互层土厚7 m，粉砂层与粉质粘土厚度相同，均为0.5 m；顶部覆盖有4.0 m厚的粘土层。在x=25 m至x=35 m范围内为基坑开挖的范围，宽10.0 m，基坑周边设置两道地下连续墙，连续墙深16 m，插入比为1.0，墙厚1.0 m。围护结构用程序中的实体单元进行模拟。

将x水平方向的边界x=0 m、x=60 m及z方向模型底部边界z=0 m的竖直方向（z方向）位移进行约束，模型的顶部z=20 m则为自由边界。所有单元在y方向的位移均被约束，而只分析互层土体在xoz平面范围的位移变化，土体本构模型采用摩尔—库伦塑性模型。

图1 数值计算模型图

1.2 模型参数

土层条件及参数选以武汉华润万象城基坑工程为例，计算模型中考虑地下水与土体的耦合，对于计算过程中土体体积的变化，由土体颗粒的本身的压缩性带来的变量可以忽略不计，因此设置土体biot系数为1。土体的抗拉强度赋值时砂土抗拉强度取为0，粘土的抗拉强度依据部分学者的研究结果[13-15]进行取值。各类土体参数采用有效应力指标，具体数值见表1。

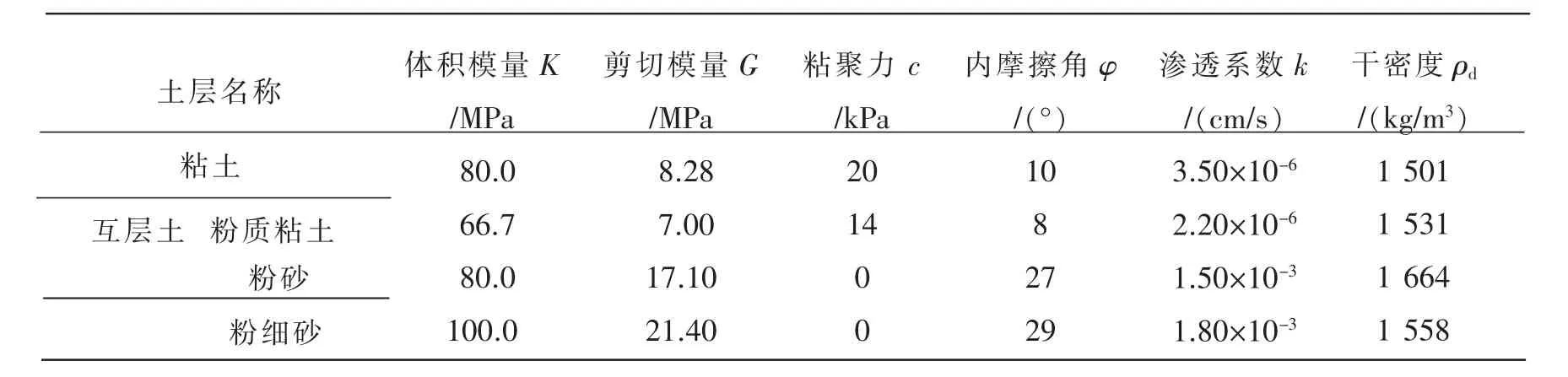
表1 模型各土层的物理力学参数表

支护结构为地下连续墙，采用C30混凝土，混凝土刚度乘0.8折减系数后，弹性模量取为24 GPa，泊松比取为 0.2，密度为 2 500 kg/m3。

1.3 初始状态

下部砂层承压水水头位于互层土层顶板之上3 m，互层土水头位于其顶部上方1 m。土层中初始孔隙水压力分布如图2。模型建立完成且参数赋值完毕后，设置重力场、开始初始应力计算。此时，计算过程中应约束模型底部的孔隙水压力，使其表现为透水边界。

由于土体、尤其是粘土层的固结会伴随超静孔隙水压力的产生，而其消散的过程十分缓慢，往往模型土体变形达到稳定后，超静孔隙水压力仍然存在。为解决这一问题，需要多次初始化孔隙水压力，通过这步计算，可以使土体在重力作用下固结压缩，从而达到接近土体自然状态下的平衡状态。计算完成后，将所有单元位移清零，才开始模拟突涌破坏的计算。

图2 初始孔隙水压力分布

2 数值模拟结果分析

突涌破坏模拟时，在下部细砂层底部中施加固定水压，使其表现为透水边界。同时将基坑底面孔隙水压力固定为0，即模拟地下水渗出地面后被及时排出。模拟过程分多步进行，每次开挖1.0m土体，求解至基坑变形达到稳定状态。模拟过程中，调用程序内部的FISH语言进行土层应力应变的监测，可以清晰的记录土层破坏过程。

2.1 工况1——开挖互层土上覆不透水粘土层

初始固结完成后，首先开挖上覆不透水粘土层，使用FLAC3D中model null命令模拟每次开挖1.0 m土体，开挖一层土后，待求解稳定再开挖下一层土，依次往复直至开挖到指定深度。求解过程中以隔水层中塑性区域的贯通作为突涌的判定标志，记录土体的变形过程，同时利用自定义的Fish程序监测土体内部的屈服状态，记录过程中的相关数据，图3为开挖深度1.0～4.0 m时基坑土体的竖向变形云图。

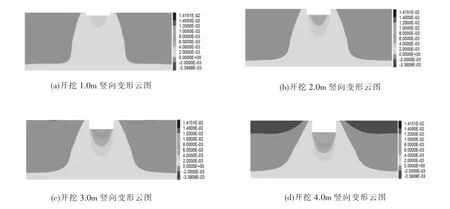
图3 工况1土体竖向变形云图

从图3中可知

（1）在坑内土体被挖除后，坑内土体由于上覆土压力被卸载而向上部隆起，其隆起值基坑中心最大，向两边逐渐减小。

（2）随着基坑不断的开挖，坑内土体隆起值也不断增大，同时隆起范围也由基坑中心不断向坑边发展。在开挖深度到4.0 m时，坑内隆起达到最大约1.1 cm。

（3）从垂直方向上来看，基坑内土体竖向变形影响范围也随着开挖进行而不断向下部拓展。

（4）在开挖过程中，坑内土体隆起速率较小且平稳，未发生竖向土体急剧变形现象，基坑处于稳定状态。

为了进一步记录基坑开挖过程中土体的应力状态，在模拟中采用中张传庆[8]提出的屈服接近度来对土体单元进行监测。屈服接近度就是土体应力状态接近屈服状态的程度，其值在0～1之间，当接近1时，说明此时土体趋于稳定；而当其接近0时，就表明土体所受应力接近其屈服强度准则，即将达到屈服状态。模拟过程中，利用程序自带的Fish语言来实现基于摩尔—库伦准则的屈服接近度函数。每开挖一层土，就调用一次函数，得到基坑土体屈服接近度分布情况。图4为开挖1.0～4.0 m时基坑土体屈服接近度云图。

图4 工况1土体屈服接近度云图

由图4可知

（1）在基坑开挖到2.0 m深度过程中，坑内土体均未达到塑性状态，处于稳定状态。到开挖深度达到2.0 m时，坑内土体屈服接近度由上至下依次增加，表明基坑表面的土体将更易发生破坏。

（2）在开挖2.0～4.0 m时，基坑底土体屈服接近度较小的区域自坑底表面以一定角度向下方发展，这些区域的土体将随着开挖进行率先进入到塑性阶段。

（3）坑内土体的屈服接近度由上至下逐渐增加，即土体随深度增加而趋于稳定。即：在开挖过程中坑内土体的屈服与破坏是从上至下依次发展的。

（4）互层土中粉砂层中屈服接近度较小区域随着基坑的开挖由两侧迅速向中间发展，最终整层粉砂均接近于屈服；而对于互层土中粘土层，其接近屈服的区域仅在基坑内边缘位置与上下粉砂层连通。

模拟中以隔水层塑性区贯通作为突涌发生的判定标准，图5为工况1开挖过程中土体单元的塑性区域，可以看出：

（1）开挖到2.0 m时中，基坑内土体均处于弹性变形阶段，其所受应力未达到屈服强度。

（2）开挖到3.0 m处时，互层土最顶部的粉砂层开始出现剪切屈服，其屈服区域较小，集中于坑底两侧，且其上下土层中均未出现屈服区域。

（3）开挖深度达到4.0 m、即互层土上覆不透水粘土层被全部挖除后，互层土最顶部及其相邻的下一层粉砂层中出现了大区域的剪切屈服区域，在坑底两侧还出现拉张屈服。对应到工程实际，此时便是互层土顶部砂性土释水阶段，伴随有“流水”、“流砂”现象。但这两层粉砂层中间的粉质粘土一直处于稳定弹性变形阶段，阻隔了两层砂性土层的塑性区域的贯通，即释水现象只发生于互层土1～2m范围内的粉砂层中，不会形成自下而上的涌水、涌砂的突涌破坏。

（4）对比土体屈服接近度云图与土体塑性区域图可以发现，土体屈服接近度与土体塑性区具有一致性，可以利用土体屈服接近度来预测土体中塑性区的产生区域。

图5 工况1土体塑性区域分布图

2.2 工况2——开挖互层土层

此阶段模拟分析时每次开挖1.0 m，直至发生坑底突涌，具体结果如图6～9。

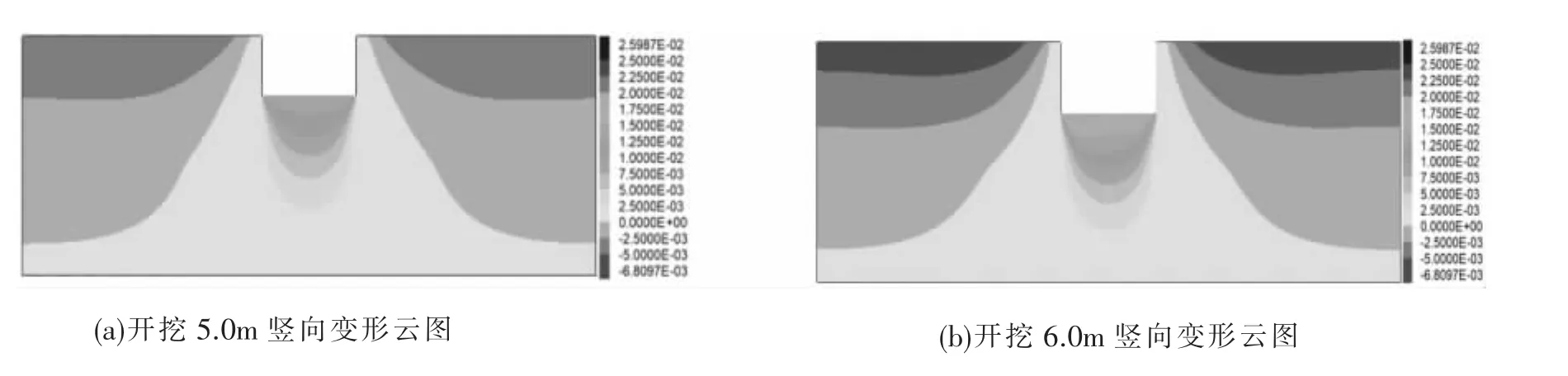
图6 工况2土体竖向变形云图

（1）从图6坑底土体隆起变形来看，坑底土体的隆起值不断加大，在开挖到6.0m时，坑底的隆起值达到了2.6cm。单从基坑土体的隆起值判断，基坑坑底土体应处于正常状态，未发生变形过大的渗透破坏。

（2）图7为开挖过程中隆起值随开挖深度的变化曲线。从该曲线可知，在开挖深度到5～6 m时，其坑底土体的隆起速率具有明显的增大。坑底土体隆起变形已由缓慢匀速变形阶段发展到逐渐加速变形阶段，在此阶段基坑底板趋于不稳定，随时可能发生突涌。

（3）图8为工况2条件下土体屈服接近度云图，从图中可以看出土体屈服接近度接近0的区域相比工况一有了大幅度的增加，互层土内上部区域无论是粉砂层还是粉质粘土层均已接近屈服。

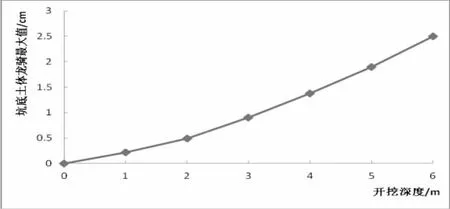
图7 坑底土体隆起值与开挖深度曲线

图8 工况2土体屈服接近度云图

（4）屈服接近度接近0的区域在互层土中呈梯形分布。当开挖深度达6 m时，屈服接近度接近0的区域已向下发展至下部砂层中，据此分析基坑内互层土层整体上接近不稳定，且土层内可能发展贯通至下部砂层的塑性区域，存在较大的坑底突涌风险。

（5）图9为开挖互层土层时土体的塑性区域分布图。从图中可以看出在开挖到5 m时，互层土层除了顶层进入了剪切屈服状态，其内部也开始出现塑性区，但塑性区成层分布，相互之间没有连通，因此此时坑内互层土体趋近不稳定，但还没有发生突涌破坏。

（6）在开挖至6 m时，互层土层内塑性区大幅增加，并且上下之间相互联系，由基坑坑底边缘以一定的角度（约60°）向下方拓展，直至达到细砂层，形成了由坑底贯通至下部砂层的塑性区域，这就明显标志着基坑处于突涌不稳定状态。

图9 工况2土体塑性区域分布图

3 结论

运用数值模拟方法，模拟了互层土基坑中坑底突涌的发展过程：在开挖互层土层上覆粘土层时，基坑整体处于稳定状态，仅顶部部分区域出现塑性屈服，达到了突涌不稳定状态；在开挖互层土层时，土体的塑性区域不断向下方发展，最终以一定角度与下方砂层塑性区贯通，基坑发生突涌。认为数值模拟应以塑性区贯通作为突涌发生的判定标志。