基于加工模型的大重合度齿轮时变啮合刚度计算
黄 康,杨 磊,徐 锐,汝 艳,邱明明,孙 浩
基于加工模型的大重合度齿轮时变啮合刚度计算
黄 康1,杨 磊1,徐 锐2,汝 艳3,邱明明1,孙 浩1
(1. 合肥工业大学机械工程学院,合肥 230009;2. 安徽工程大学机械与汽车工程学院,芜湖 241000;3. 中国人民解放军陆军炮兵防空兵学院,合肥 230031)
针对大重合度齿轮实际加工齿廓的过渡曲线、齿顶修缘、齿厚均与理想齿廓有所不同,对其啮合时变刚度计算方法进行了研究,建立了凸角修缘类型滚刀参数方程,依据齿轮啮合原理,推导剃(磨)齿前滚刀参数方程以及剃(磨)齿后齿轮齿廓的参数方程,结合现有计算大重合度齿轮时变啮合刚度的能量法,设计了改进势能法模型.根据齿廓参数方程编制了大重合度齿轮模拟软件,基于有限元软件计算出齿轮时变啮合刚度.将改进势能法模型与有限元法模型求解出来的结果进行对比,得出改进势能法模型的计算结果与有限元分析结果有较好的一致性,证明了所提出的改进势能法模型具有有效性.利用改进势能法模型研究了齿厚、过渡曲线、齿顶修缘对单齿啮合刚度最大值以及时变啮合刚度均值的影响.结果表明:齿厚对单齿啮合刚度最大值以及时变啮合刚度均值影响较大;过渡曲线部分主要的影响参数——凸角凸出部分径向高度、凸角径向高度、滚刀齿顶圆弧的半径对单齿啮合刚度最大值以及时变啮合刚度均值影响较小;齿顶修缘参数中的加工滚刀的修缘高和修缘角对单齿啮合刚度最大值的影响较小,但是对齿轮啮合刚度均值影响较大.
剃(磨)齿;大重合度;时变啮合刚度;改进势能法;有限元法
随着对齿轮传动中振动和噪声要求的提高,人们开始关注不同设计方法的发展,其中,通过改变轮齿齿高来提高齿轮重合度(即设计大重合度直齿轮)是一种重要的减振降噪手段.相对于普通重合度(重合度小于2)直齿轮,大重合度(重合度大于2)直齿轮在啮合过程中,参与啮合的轮齿对数增多,单对轮齿承受载荷降低,因而采用大重合度齿轮能够有效提高系统的承载能力和运动平稳性[1-3].由于大重合度齿轮传动时涉及到多齿同时啮合,啮合轮齿的受力分析较为繁琐,从而导致其弹性变形的计算过程也变得非常复杂[4].因此,计算大重合度直齿轮的啮合刚度,对大重合度直齿轮的承载能力计算和动力学分析具有重要意义[5-7].
目前国内外很多学者研究齿轮啮合刚度.李亚鹏[8]进一步修正了石川公式.Yang等[9]利用势能法计算了齿轮的啮合时变刚度.在Yang等[9]的基础上,Wu等[10-11]考虑轮齿剪切势能将总势能分成了4部分. Zhou等[12]将轮齿简化为半悬臂梁,改进了啮合刚度的计算方法.文献[9-12]认为基圆与齿根圆重合,但在齿轮齿数达到一定数量以后,求解结果与有限元分析结果相差较大.依据文献[9-12]的成果,万志国等[13]提出了齿根圆与基圆不重合的改进方法,但是该方法计算齿轮啮合刚度,必须提前确定齿数.在万志国等[13]的基础上,马辉等[14]提出的基于改进能量法的直齿轮时变啮合刚度计算方法避开了齿数的判断.Yong等[15]利用势能法计算直齿轮修形,磨损时齿轮的啮合时变刚度.以上学者的研究对象大多数是理论渐开线齿廓,并没有考虑齿轮的实际加工状况.实际上,大部分齿轮在滚刀粗加工以后,还需要再进行剃(磨)齿等精加工,而剃(磨)工艺对齿轮的齿形有较大影响,从而导致实际齿形的时变啮合刚度计算方法相对于理论齿廓的计算方法会很有大区别.目前,针对考虑实际加工模型的时变啮合刚度计算的文献尚不多见.
本文根据已有文献,考虑了剃(磨)齿齿轮实际模型的齿廓曲线,利用势能法求解齿轮的时变啮合刚度.其次,利用齿廓参数方程,编写大重合度齿轮模拟软件,实现了大重合度齿轮自动化、参数化建模,通过有限元分析计算,进一步提高齿轮时变啮合刚度的计算精度.然后将本文提出的改进势能法模型与有限元分析结果对比,验证本文势能法模型的正确性.最后,用该势能法模型分析了齿厚、过渡曲线、齿顶修缘对大重合度齿轮时变啮合刚度的影响,揭示了大重合度齿轮时变啮合刚度变化的主要影响因素.
1 基于实际加工模型的大重合度齿轮齿廓曲线方程
1.1 建立剃(磨)齿前滚刀参数方程
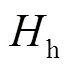
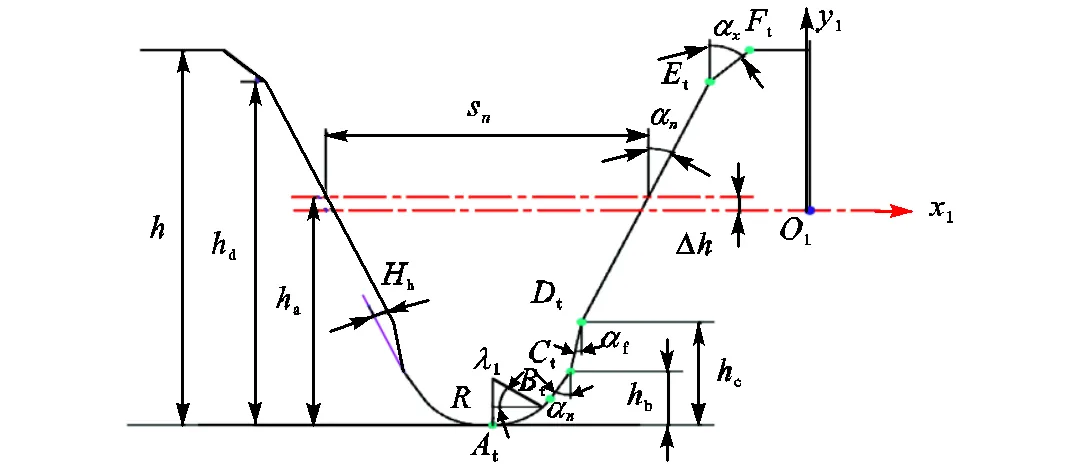
图1 剃(磨)前修缘类型滚刀
tt方程为
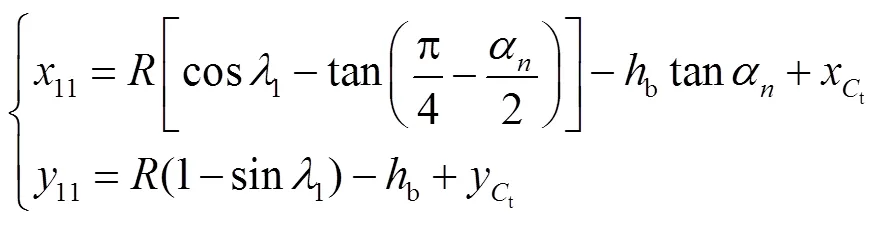
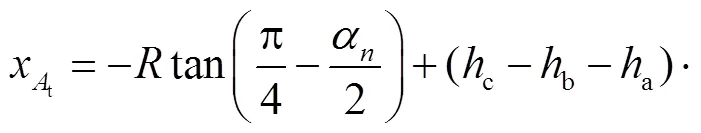
tt方程为
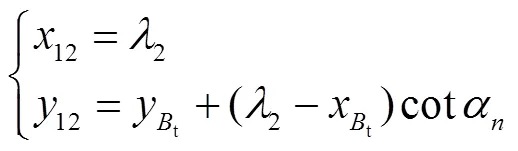
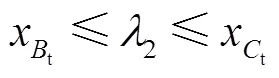
tt方程为
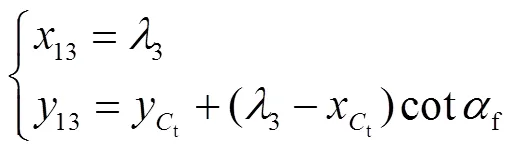
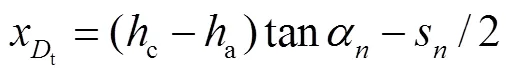
tt方程为
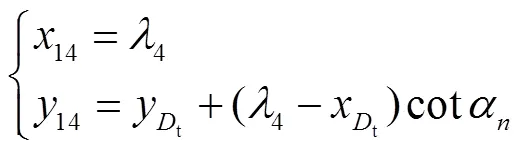
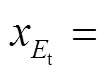
tt方程为
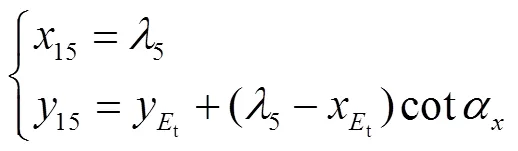
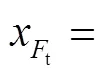
1.2 建立剃(磨)齿前齿面轮廓方程
将上述滚刀坐标系各段参数方程转换到齿轮坐标系中,即可得到对应滚刀的齿轮齿廓曲线方程.为了实现坐标转换,建立如图2所示的滚刀齿轮坐标系.其中,为固定坐标系,111为滚刀坐标系,222为齿轮坐标系.
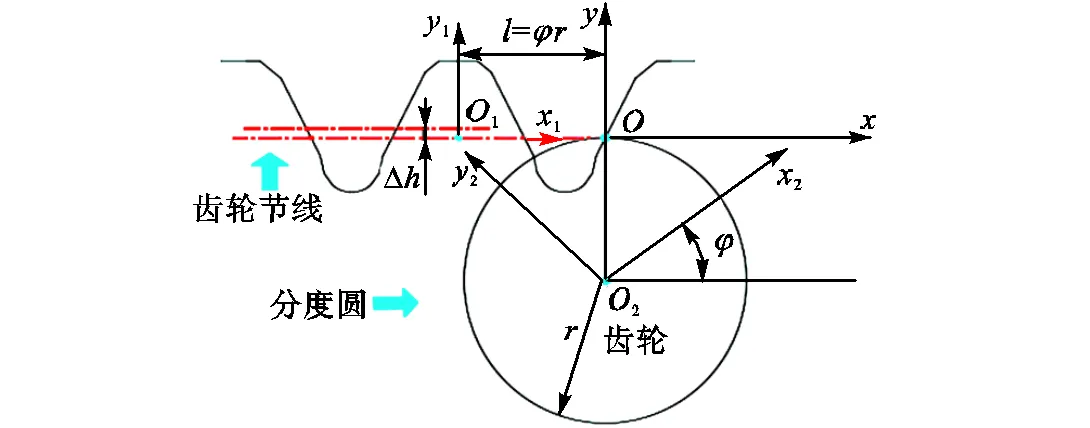
图2 滚刀与齿轮的运动坐标
坐标系222到坐标系的变换矩阵02为
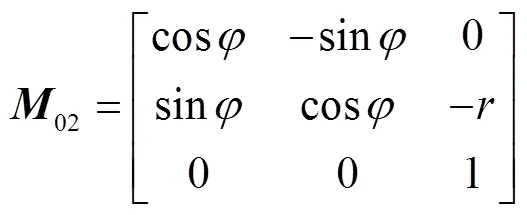
式中:为齿轮的节圆半径;为齿轮从初始位置开始旋转的角度.
坐标系到坐标系111的变换矩阵10为
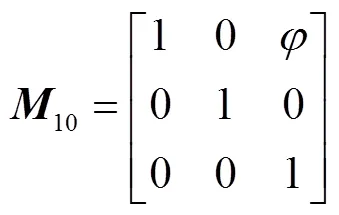
坐标系222到坐标系111的变换矩阵21为
根据齿轮啮合原理可知,齿轮齿廓曲线由刀具齿廓tt段形成.则当=1时,齿轮轮齿齿廓曲线的坐标表达式为

当=2时,齿轮轮齿齿廓曲线的坐标表达式为

那么,当=3时,段的参数方程为

当=4时,段的参数方程为
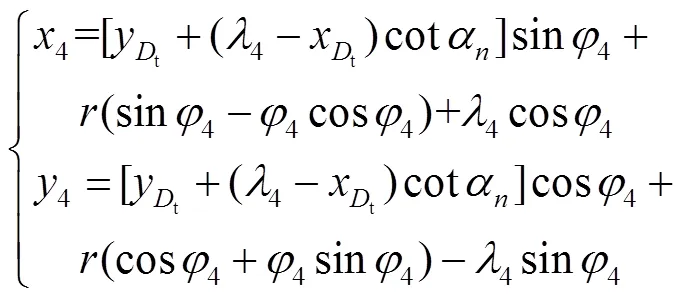
当=5时,段的参数方程为
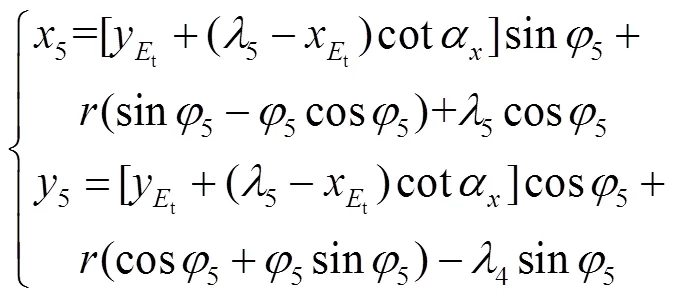
1.3 建立剃(磨)齿后滚刀参数方程
剃(磨)后滚刀的基本作用是针对剃(磨)前滚刀加工出来的齿轮进行精加工.如图3所示,剃(磨)后滚刀的齿廓曲线由tt、tt、t、、t段构成,图中,s表示剃(磨)前滚刀主切削刃tt平移到剃
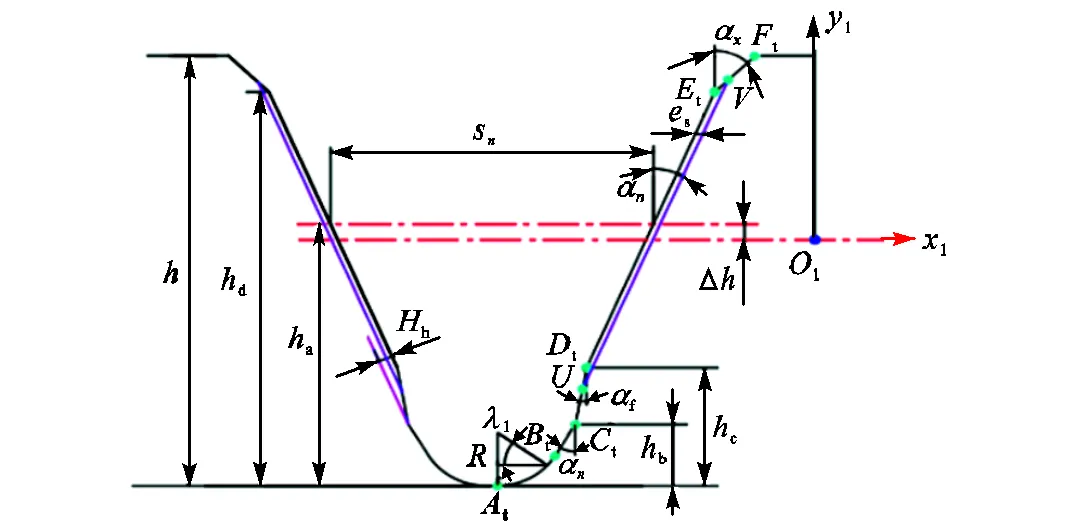
图3 剃(磨)后修缘类型滚刀
(磨)齿后滚刀主切削刃段的距离.
的参数方程为
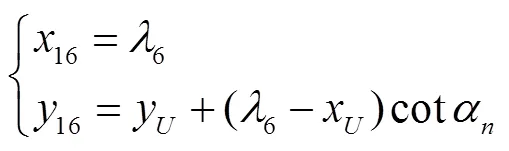
、的坐标分别为
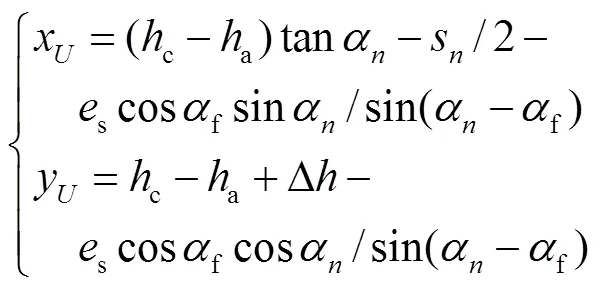
1.4 建立剃(磨)齿后齿面轮廓方程
如图4所示,′点为tt形成的过渡曲线与剃后渐开线的交点,即为剃(磨)齿后形成的实际的渐开线起始点,同理,′点为渐开线终止点.剃(磨)后渐开线的曲线方程可以表示为

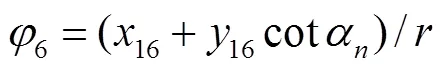
2 大重合度齿轮啮合刚度计算
啮合齿轮中的势能有赫兹接触势能h、齿基势能f、弯曲势能b、剪切势能s和轴向压缩势能a,这5种势能可以分别求解赫兹接触刚度h、齿基刚度f、弯曲刚度b、剪切刚度s和轴向压缩刚度a.
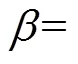
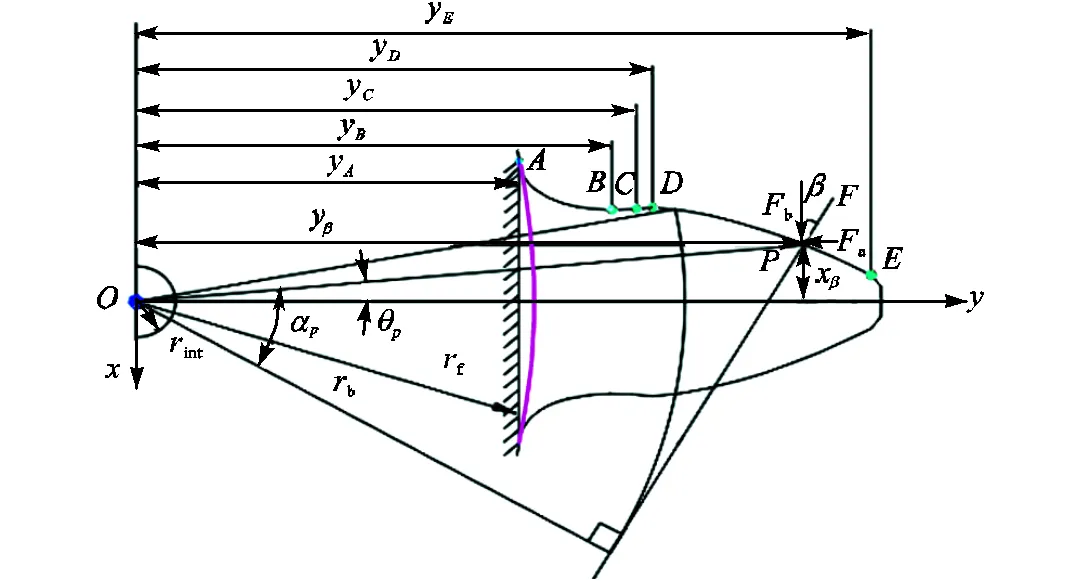
图5 齿轮受力示意
由材料力学及弹性力学,可得
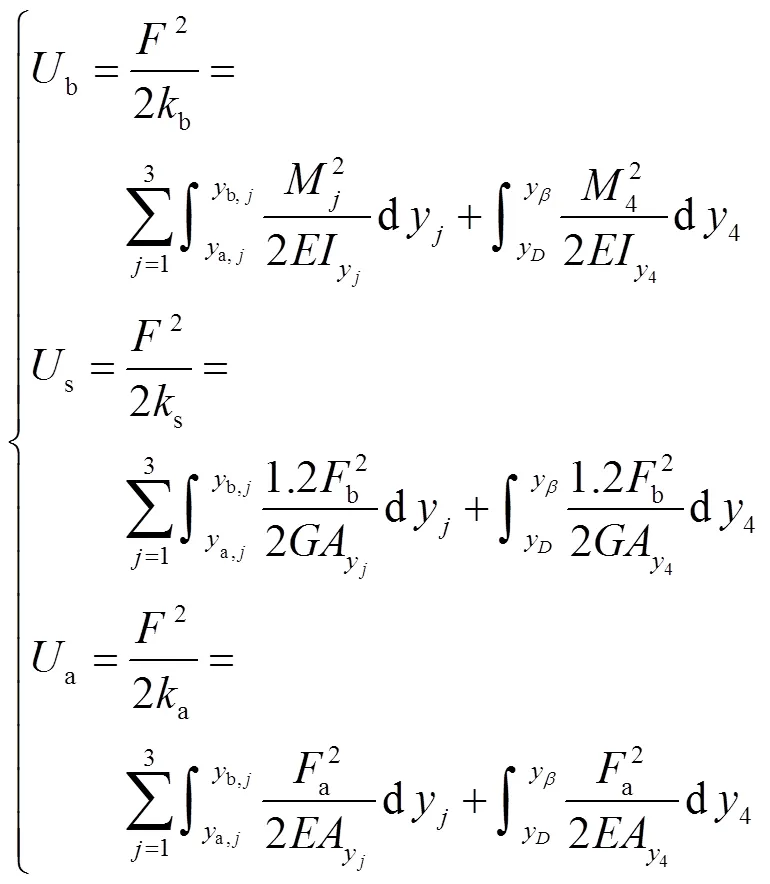
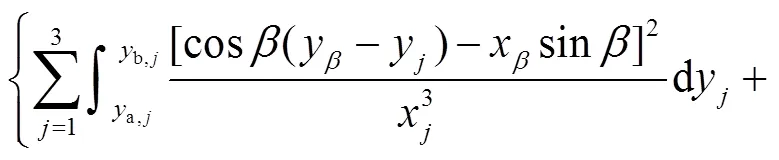

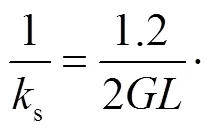

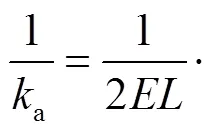
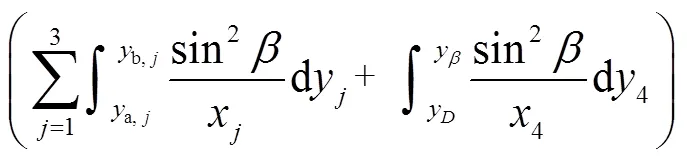
齿轮的接触刚度[17-18]为
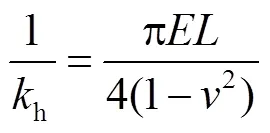
式中:为齿宽;为泊松比.
齿基刚度的计算式为

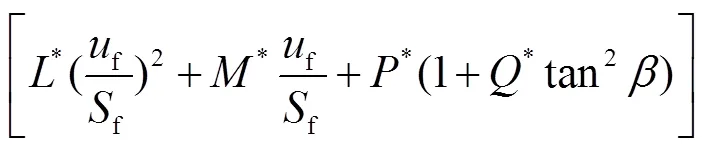
式(17)中具体参数参考文献[19-20].
由文献[15]可知,有1对、2对或3对轮齿同时啮合时,啮合齿轮的总体刚度为
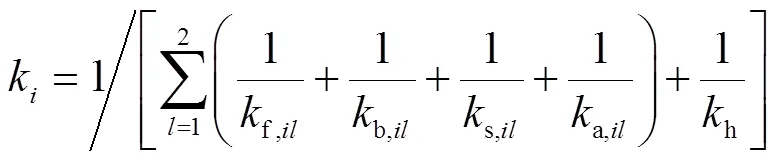
3 仿真分析与验证
3.1 有限元法求齿轮啮合刚度原理
对于单齿对综合啮合刚度,根据文献[21]有
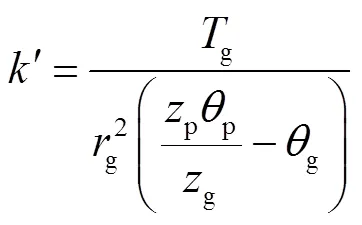
对于多齿对综合啮合刚度,根据文献[22]有
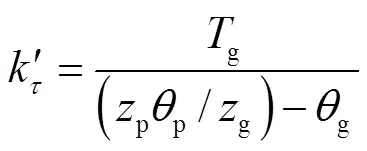
3.2 大重合度齿轮建模与仿真
本文通过VB语言编写大重合度齿轮软件,使齿轮建模参数化,通过输入凸角修缘类型滚刀参数(见表1),生成相应大重合度齿轮二维图,将其导入Solidworks中建立大重合度齿轮三维模型.两齿轮材料为45号钢,齿宽=26mm,小齿轮齿数1=25,大齿轮齿数2=32,大、小齿轮模数=3.25,中心距=91.5mm,两个齿轮的内孔直径都取为对应齿根圆直径的30%.大齿轮内孔约束所有自由度,小齿轮内孔只保留旋转的旋转自由度,建立如图6所示的大重合度齿轮有限元模型.通过有限元模型求解出单齿啮合综合刚度以及多齿啮合综合刚度.
表1 凸角修缘类型滚刀参数
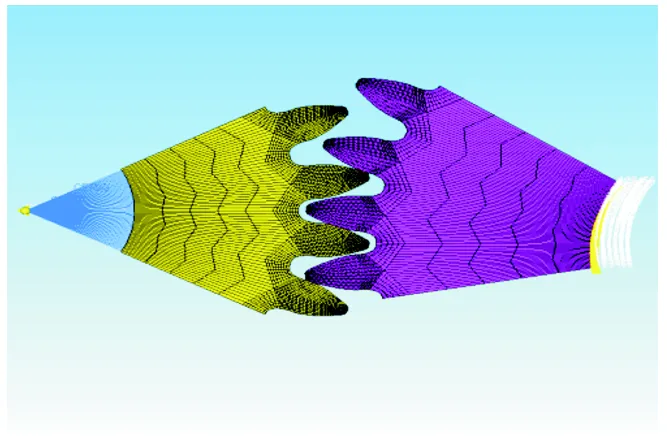
图6 大重合度齿轮有限元模型
3.3 分析与验证
考虑到载荷对时变啮合刚度有非线性影响,在不同载荷0.5、1.0和2.0作用下分别对齿轮单齿啮合刚度以及多齿轮啮合刚度均值进行对比,得到单齿和多齿齿轮啮合刚度曲线如图7和图8所示.
由图7和图8仿真分析可知,在相同的载荷下,本文模型求解结果与仿真结果有较好的一致性,证明了本文势能法模型的有效性;有限元分析结果比势能法仿真结果偏大,主要原因是有限元分析时,小齿轮和大齿轮的内孔建立的都是刚性耦合,同时接触刚度设置为每次迭代计算以后自动更新,控制卡片里面的几何非线性打开大变形开关.
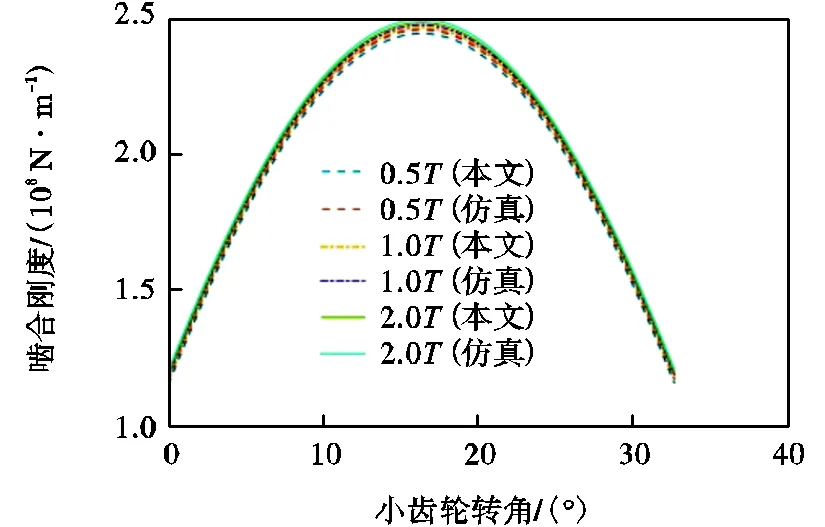
图7 单齿啮合刚度曲线
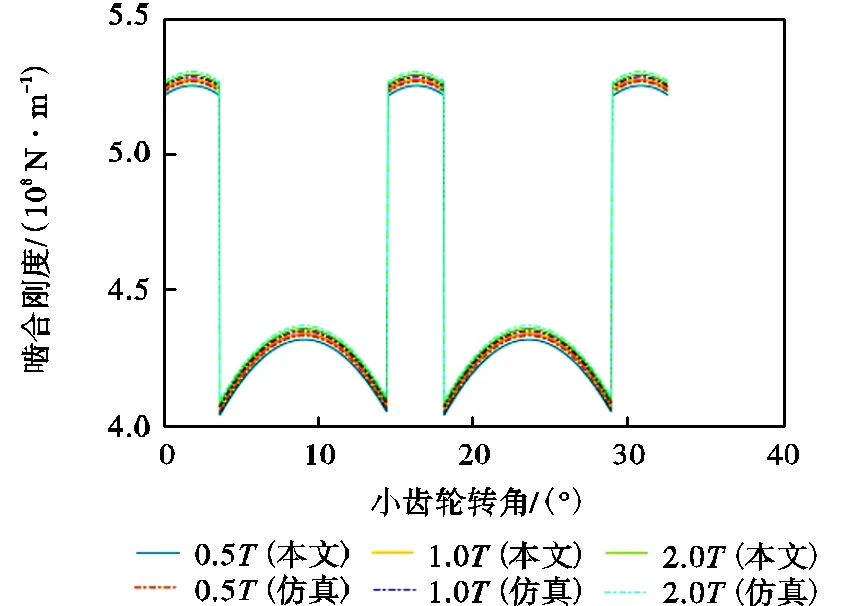
图8 多齿啮合刚度曲线
3.4 实际加工模型对齿轮啮合刚度的影响
图9比较了3种方法单齿啮合刚度和时变啮合刚度的变化情况.以表1为例,第1种研究方法是李发家[3]利用材料力学方法求解的结果与所提出的模型相比,单齿啮合刚度最大值以及时变啮合刚度均值各自增加7.66%和9.09%左右.这是因为李发家[3]分析的是理想齿廓,未考虑剃(磨)齿齿轮实际加工模型的实际齿廓等影响因素.第2种研究方法是Yong等[15]考虑齿轮修形、磨损时啮合刚度模型,与所提出的模型相比,单齿啮合刚度最大值以及时变啮合刚度均值各自增加3.23%和4.66%左右,这是因为Yong等[15]分析的模型未考虑经剃(磨)齿加工后齿轮齿廓的过渡曲线、齿顶修缘等参数对齿轮时变啮合刚度的影响.
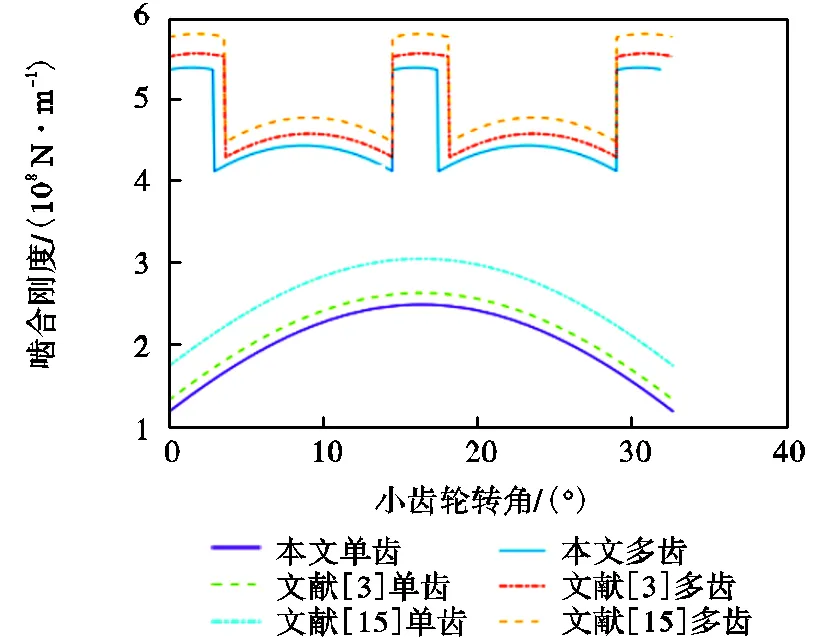
图9 3种模型啮合刚度曲线
3.5 啮合刚度影响因素分析
根据前文的分析,齿轮实际加工齿廓的齿厚、过渡曲线、齿顶修缘等均与理想齿廓有所不同,从而导致实际齿廓和理想齿廓的轮齿刚度存在差异,接下来本文将分析这些因素对大重合度齿轮啮合刚度的影响.
3.5.1 齿厚
为了防止由齿轮中心距安装误差、工作时因摩擦发热等原因引起啮合齿轮卡住的现象以及使齿轮啮合当中形成润滑油膜来减少摩擦,两啮合齿轮之间必须留有一定的间隙.由于齿厚变小,齿轮的啮合刚度必然会发生变化,而在以往的刚度计算中,均以理想齿廓为主,并没有考虑齿厚变化对刚度计算的影响.因此,本文将利用改进势能法分析不同齿厚变化量对大重合度齿轮啮合刚度的影响.
设两齿轮齿厚变化相同,即总的齿厚减少了2s.图10所示为当s分别为0、0.075mm、0.150mm时的大重合度齿轮单齿和多齿的时变啮合刚度曲线.由图10可知,当s从0mm增加到0.075mm时,单齿刚度下降2.10%,多齿刚度下降2.50%;当s从0mm增加到0.150mm时,单齿刚度最大值下降了4.13%,多齿啮合刚度均值下降了4.90%.由此可见,s对齿轮的时变啮合刚度变化的影响比较明显.

图10 不同齿厚情况下齿轮啮合刚度曲线
3.5.2 过渡曲线
齿轮的过渡曲线部分主要由凸角凸出部分径向高度b、凸角径向高度c、滚刀齿顶圆弧半径来确定.如图11所示,当h=0.04mm,=0.5mm,b分别取0.50mm、1.25mm、2.00mm时的大重合度齿轮单齿和多齿的时变啮合刚度变化情况.可以看出,随着b的增加,大重合度齿轮时变啮合刚度有一定的减少,这主要是因为当b增加时,渐开线起始点随之增加,从而导致渐开线部分变短.b从0.50mm变化到2.00mm,大重合度齿轮的单齿啮合最大值下降1.45%,时变啮合刚度均值下降1.70%.
如图12所示,当b=0.50mm,=0.5mm,h分别取0.04mm、0.09mm、0.14mm时的大重合度齿轮单齿和多齿的时变啮合刚度变化情况.可以看出随着h的增加,大重合度齿轮的啮合刚度会逐渐减少.当h从0.04mm变化到0.13mm时,大重合度齿轮单齿啮合刚度最大值下降3.4%,时变啮合刚度均值下降4.02%.由图11和图12易知,h比b对啮合刚度的影响更加明显,其主要原因是当h增加时,过渡曲线不断向轴移动,导致渐开线起始点向上移动和整个齿根宽度变窄.
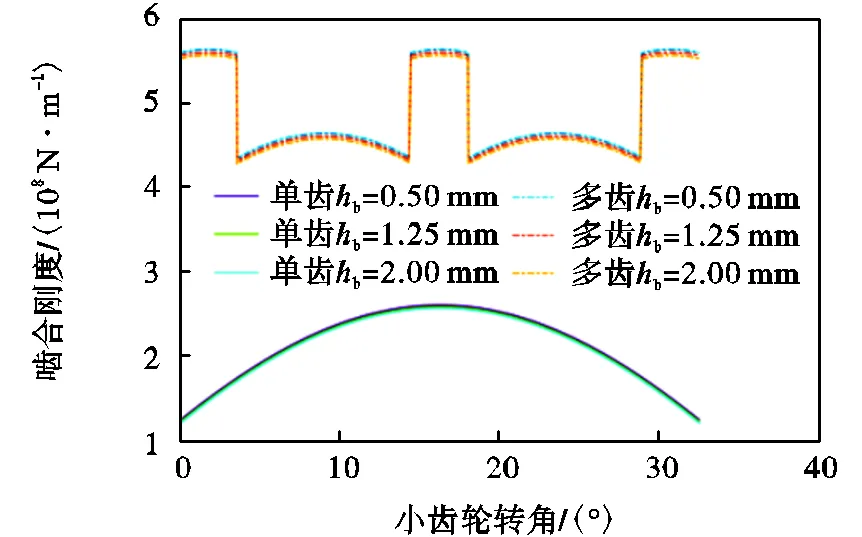
图11 hb对齿轮啮合刚度的影响
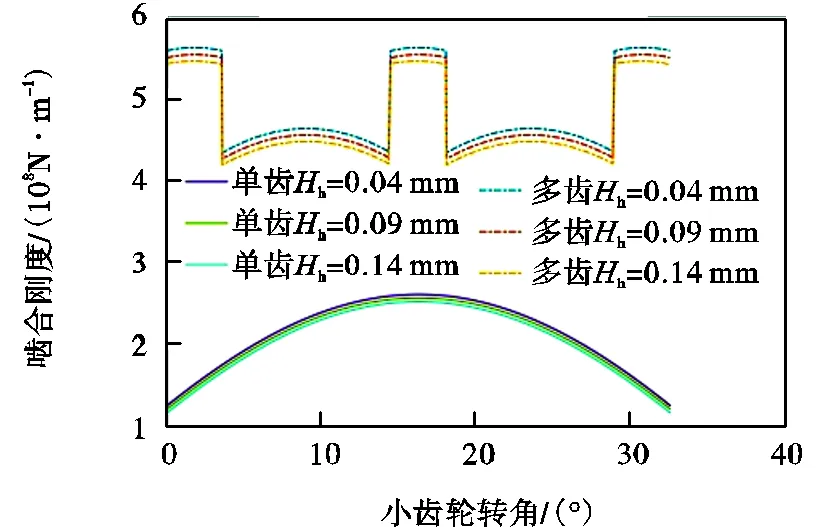
图12 Hh对齿轮啮合刚度的影响
如图13所示,当b=0.50mm,h=0.04mm,分别取为0.4mm、0.6mm、0.8mm时的大重合度齿轮单齿和多齿的时变啮合刚度变化情况.可以看出,随着的增加,大重合度齿轮的刚度会逐渐增加,与b和h对齿轮的啮合时变刚度影响规律截然相反.当从0.4mm变化到0.8mm时,大重合度齿轮的单齿啮合刚度最大值增加1.71%,时变啮合刚度均值增加2.09%.其增大的主要原因是当的增加接近齿根圆时,过渡曲线部分曲率变小,使得齿根弯曲强度得以提高.
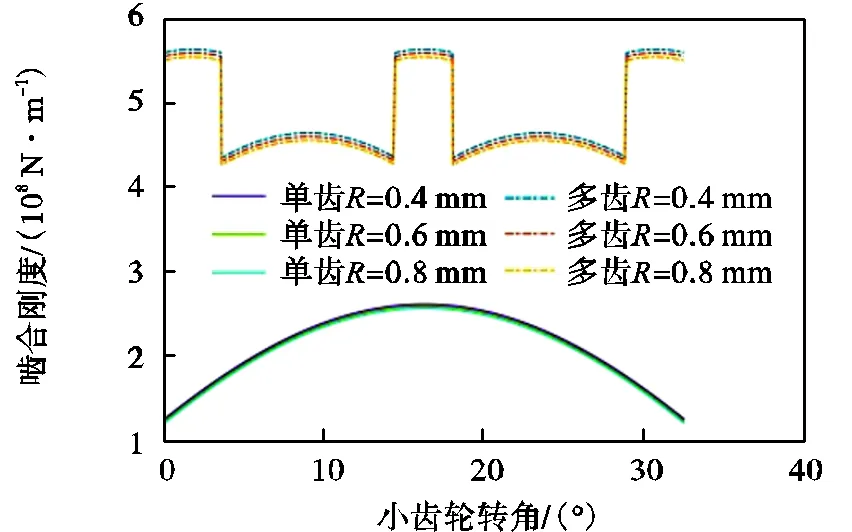
图13 R对齿轮啮合刚度的影响
3.5.3 齿顶修缘
齿顶修缘主要由滚刀的修缘高d以及修缘角α确定.齿顶修缘对单齿啮合刚度最大值影响很小,主要通过改变渐开线终止圆的半径来影响齿轮进入和退出啮合时间,从而改变双齿和三齿的啮合状态.下面主要分析修缘高d以及修缘角α这两个参数对大重合度齿轮啮合刚度的影响.
如图14所示,当=55°,d=0.6mm、0.8mm、1.0mm时的大重合度齿轮单齿和多齿的时变啮合刚度的变化情况.可以看出,随着d的增加,大重合度齿轮的单齿啮合刚度曲线基本没有变化,但是由于渐开线啮合长度随之变短,造成重合度降低,导致齿轮的啮合刚度均值发生比较明显的变化.当d从0.6mm变化到1.0mm,大重合度齿轮的啮合刚度均值下降了5.2%.
如图15所示,当d=0.8mm,分别取30°、45°、60°时的大重合度齿轮单齿和多齿时变啮合刚度的变化情况.由图15可以看出,同样会造成重合度降低,齿轮的啮合刚度均值发生比较明显的变化.当从30˚变化到60˚,大重合度齿轮的啮合刚度均值下降了3.4%.
通过上述分析可知,虽然d和α对单齿啮合刚度最大值影响比较小,但是它们改变了齿轮渐开线的啮合长度,使得齿轮重合度降低,对多齿啮合刚度均值影响较大,因此在设计齿轮的时候,齿轮的修缘部分设计不容小觑.
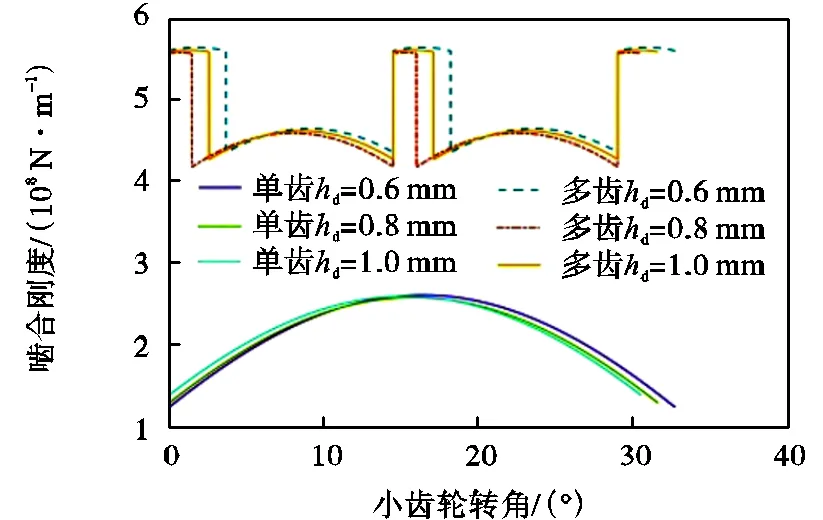
图14 hd对齿轮啮合刚度影响

图15 ax对齿轮啮合刚度的影响
4 结 论
(1)精确建立凸角修缘类型滚刀参数方程,设计开发了改进势能法模型,对现有势能法计算大重合度齿轮时变啮合刚度进行完善.
(2) 利用齿廓参数方程,编写大重合度齿轮模拟软件,实现了自动化、参数化建模,提高了建模的精确性,而且模型修改简单化,大大提升了仿真速度.
(3) 通过本文的分析可知,齿厚对单齿啮合刚度最大值以及时变啮合刚度均值影响较大,过渡曲线对齿轮啮合刚度变化影响较小,齿顶修缘参数对单齿啮合刚度的最大值影响比较小,但是对齿轮啮合刚度均值有较明显的影响.
[1] Ye S Y,Tsai S J. A computerized method for loaded tooth contact analysis of high-contact-ratio spur gears with or without flank modification considering tip corner contact and shaft misalignment[J]. Mechanism and Machine Theory,2016,97:190-214.
[2] Pandya Y. Crack behavior in a high contact ratio spur gear tooth and its effect on mesh stiffness[J]. Engineering Failure Analysis,2013,34(34):69-78.
[3] 李发家. 大重合度行星齿轮传动系统强度及动力学研究[D]. 南京:南京航空航天大学,2015.
Li Fajia. The Strength and Dynamics Analysis of Hight Contact Ratio Planetary Gear Transmission[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2015(in Chinese).
[4] Nishino T. Integrated excitation models of the helical gear system[C]//ASME Design Engineering Technical Conferences. Las Vegas,NV,USA,2007:DETC2007-34134.
[5] Liang X H,Liu Z L,Pan J,et al. Spur gear tooth pitting propagation assessment using model-based analysis[J]. Chinese Journal of Mechanical Engineering,2017,30(6):1369-1382.
[6] 张 娟. 大重合度变速器齿轮的承载能力研究[D]. 合肥:合肥工业大学,2014.
Zhang Juan. Study on the Bearing Capacity of Transmission Gears with Large Coincidence[D]. Hefei:Hefei University of Technology,2014(in Chinese).
[7] Alves J T,Wang J,Guingand M. Static and dynamic models for spiral bevel gears[J]. Mechanics & Industry,2013,13(5):325-335.
[8] 李亚鹏. 齿轮时变啮合刚度改进算法基刚度激励研究[D]. 大连:大连理工大学,2009.
Li Yapeng. Study on Improved Algorithm of the Time-Varying Meshing Stiffness of Gear and Stiffness Excitation[D]. Dalian:Dalian University of Technology,2009 (in Chinese).
[9] Yang D C H,Lin J Y. Hertzian damping,tooth friction and bending elasticity in gear impact dynamics[J]. Journal of Mechanisms,Transmissions,and Automation in Design,1987,109(2):189-196.
[10] Wu S. Gearbox Dynamic Simulation and Estimation of Fault Growth[D]. Edmonton:University of Alberta,2007.
[11] Wu S,Zuo M J,Parey A. Simulation of spur gear dynamics and estimation of fault growth[J]. Journal of Sound and Vibration,2008,317(3/4/5):608-624.
[12] Zhou X,Shao Y,Lei Y,Zuo M. Time-varying meshing stiffness calculation and vibration analysis for a 16DOF dynamic model with linear crack growth in a pinion[J]. ASME J Vib Acoust,2011,134(1):011011-1-011011-11.
[13] 万志国,訾艳阳,曹宏瑞,等. 时变啮合刚度算法修正与齿根裂纹动力学建模[J]. 机械工程学报,2013,49(11):153-160.
Wan Zhiguo,Zi Yanyang,Cao Hongrui,et al. Timevarying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]. Journal of Mechanical Engineering,2013,49(11):153-160(in Chinese).
[14] 马 辉,逄 旭,宋溶泽,等. 基于改进能量法的直齿轮时变啮合刚度计算[J]. 东北大学学报:自然科学版,2014,35(6):863-866,884.
Ma Hui,Pang Xu,Song Rongze,et al. Time-varying meshing stiffness calculation of spur gears based on improved energy method[J]. Journal of Northeast University:Natural Science,2014,35(6):863-866,884(in Chinese).
[15] Yong Y,Jia X W,Qing H Z,et al. Mesh stiffness modeling considering actual tooth profile geometry for a spur gear pair[J]. Mechanics & Industry,2018,19(3):306-320.
[16] 徐 锐. 齿轮滚刀快速选配系统的研究与开发[D]. 重庆:重庆大学,2010.
Xu Rui. Research and Development of Rapid Selection and Matching System for Gear Hobs[D]. Chongqing:Chongqing University,2010(in Chinese).
[17] Chen Z G,Shao Y M. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis,2011,18(8):2149-2164.
[18] Cornell R W. Compliance and stress sensitivity of spur gear teeth[J]. Journal of Mechanical Design,1981,103(2):447.
[19] Sainsot P,Velex P,Duverger O. Contribution of gear body to tooth deflections:A new bidimensional analytical formula[J]. Journal of Mechanical Design,2004,126:748-752.
[20] Chaari F,Baccar M,Abbes M S,et al. Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission[J]. European Journal of Mechanics-A Solids,2008,27(4):691-705.
[21] 贵新成,李立顺,李红勋,等. 大重合度摆线内齿轮副时变啮合刚度计算与齿间载荷分配研究[J]. 机械工程学报,2018,54(21):101-112.
Gui Xincheng,Li Lishun,Li Hongxun,et al. Time-varying mesh stiffness calculation and load distribution among teeth of cycloid internal gear pair with high contact ratio[J]. Journal of Mechanical Engineering,2018,54(21):101-112 (in Chinese).
[22] 周 欣,邓康耀,田中旭,等. 渐开线齿轮传动的扭转刚度研究[J]. 机械传动,2017(6):55-60.
Zhou Xin,Deng Kangyao,Tian Zhongxu,et al. Research of the torsion stiffness of involute gear transmission[J]. Journal of Mechanical Transmission,2017(6):55-60(in Chinese).
Calculation of Time-Varying Mesh Stiffness with High Contact Ratio Gear Based on Machining Model
Huang Kang1,Yang Lei1,Xu Rui2,Ru Yan3,Qiu Mingming1,Sun Hao1
(1. College of Mechanical Engineering,Hefei University of Technology,Hefei 230009,China;2. Anhui University of Engineering College of Mechanical and Automotive Engineering,Wuhu 241000,China;3. PLA Army Academy of Artillery and Air Defense,Hefei 230031,China)
Focusing on the differences in the transition curve,top trimming,and tooth thickness between a gear with a high contact ratio and the ideal profile,a method of calculating time-varying stiffness was studied.Referring to existing literature,a parameter equation for a flange-type hob was established.According to the meshing principle of a gear,the parameter equation of the hob before shaving(grinding)teeth and the parameter equation of the gear profile after shaving(grinding)teeth were deduced.Combining the existing energy method for calculating the time-varying meshing stiffness of a gear with a high contact ratio,an improved potential energy method model system was designed and developed.Based on the parameter equation of the tooth profile,the simulation software for high contact ratio gears was developed,and the time-varying meshing stiffness of the gear was calculated using finite element software.By comparing the results of the improved potential energy method model system with those of the finite element method model,the conclusion was reached that the results from the proposed method were in good agreement with those of the finite element analysis results,which proved the effectiveness of the proposed method.The effects of tooth thickness,transition curve,and tip trimming on the maximum meshing stiffness and mean meshing stiffness of a single tooth were systematically studied using the improved potential energy method model.The results show that tooth thickness has considerable influence on the maximum meshing stiffness of single tooth and the mean meshing stiffness of time-varying meshing.The main parameters of the transition curve are the radial height of the convex corner that protrudes,the radial height of the convex angle,and the radius of the top arc of the hob,which have little influence on the maximum meshing stiffness of a single tooth and the mean meshing stiffness of time-varying meshing.In the top-trimming parameters,the trimming height and trimming angle of the machined hob have less influence on the maximum meshing stiffness of a single tooth,but have considerable influence on the mean meshing stiffness of the gear.The research results can provide a theoretical basis for dynamic analysis of spur gears with large coincidence based on the actual processing model.
shaving(grinding)teeth;high contact ratio;time-varying meshing stiffness;improved energy method;finite element method
TH113.2
A
0493-2137(2020)07-0754-09
10.11784/tdxbz201907038
2019-07-13;
2019-09-16.
黄 康(1968— ),男,博士,教授,13665606407@163.com.
杨 磊,1073428125@qq.com.
国家自然科学基金资助项目(51775156);陆军航空装备“十三五”预研专用技术资助项目(30103090201);混合动力新型机电耦合总成系统开发与集成资助项目(2017YFB0103201).
Supported by the National Natural Science Foundation of China(No.51775156),the Special Technical Projects for Pre-Research of Army Aviation Equipment in the 13th Five-Year Plan(No.30103090201),the Development and Integration of a New Hybrid Electromechanical Coupling System(No.2017YFB0103201).
(责任编辑:孙立华)

