改进二阶自抗扰控制器在永磁同步电机上的仿真应用

王斯墨，范文超

（1.北方自动控制技术研究所，太原 030006；2.驻太原地区第二军代室，太原 030006）

0 引言

永磁交流定子自动同步电机自身的主要优点之一是电机结构简单、损耗低、功率大和变化因数高。与励磁直流定子驱动同步电机自身性能相比，因为本身没有任何电动毛刷、换向器等电流驱动供电装置，不必再需要驱动产生任何无限恒功励磁定子同步动机电流。因此，永磁阀和定子电流同步器的电流、电阻损耗都较小，效率更高，励磁转矩更大、能源和控制的性能更好。但依然明显地指出存在技术成本资源消耗相对较高，启动困难等重要关键技术支撑不足。随着现代控制技术在永磁同步电机上的应用，永磁同步电机有关的控制技术也吸引了更多的人进行广泛研究［1］。

20 世纪80 年代末，自抗扰控制器技术的先驱和开拓者韩京清先生，先后自主开发和设计出了非线性自抗扰跟踪微分器、扩张状态自抗扰观测器等对信号自抗扰处理及其控制系统具有独特的功能和提高控制效率的新型非线性自抗扰动态控制器结构，提出了一系列具有特殊控制功能的非线性动态误差反馈机制，开发了最优非线性自抗扰PID、最优自抗扰控制器等一系列新型非线性自抗扰控制器［2-3］。

扩张状态观测器所需要估计的负载扰动项主要包括转速、转矩的最大变化以及阻尼系数b 和负载状态惯量j 的最大变化。在永磁同步电机对于负载状态扰动较大的运行系统设计过程中，这些控制器的参数及其扰动状态的惯量参数都会在性能上发生很大的变化。

为了有效减小负载扰动变化过大对最终控制效果的影响，本文提出一种结合了负载转矩扰动项观测器和扰动前馈控制系统的永磁同步电机自抗扰控制器的改进解决方案。针对永磁交流同步电机矢量控制系统实际运行的过程中，可能存在各种负载转矩和扰动项的变化对自抗扰控制系统性能的直接影响，设计了负载转矩观测器，使用前馈控制，将扰动项补偿到自抗扰控制器中。仿真结果表明，与二阶自抗扰控制器相比，改进的自抗扰控制器具有更优的抗负载扰动性能。

1 数学模型

1.1 永磁同步电机的数学模型

本文研究的是面装式永磁同步电机，在随转子旋转的d-q 坐标系上，永磁同步电机的状态方程［4］为

式（1）为PMSM 的矩阵形式状态方程，式中id，iq分别为d，q 轴定子电流；ud，uq分别为d，q 轴定子电压；Ld，Lq分别为d，q 轴线圈的电感；Ψr为转子磁链；ωr为电机机械角速度；pn为磁极对数；J 为电机转动惯量；B 为电机摩擦系数。

在使用id=0 的矢量控制方式时，式（1）简化如下：

永磁同步电机的运动方程［1］为

其中电磁转矩如下

1.2 二阶自抗扰控制器的数学模型

自抗扰控制技术（ADRC）［7］是韩京清教授针对传统PID 控制的缺点与不足进行了改进提出的，它的设计不受被控对象准确模型的影响，在鲁棒性和稳定性方面都比PID 有显著提高。

首先定义：

Fhan 函数：

Fal 函数：

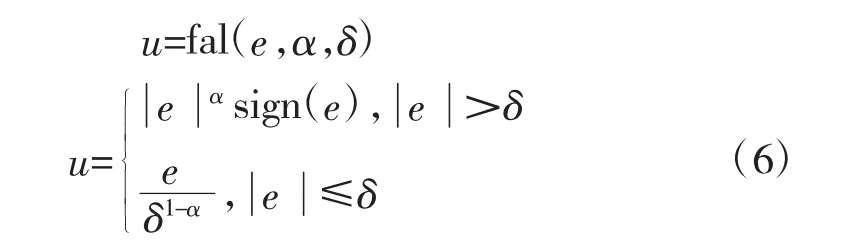
二阶ADRC 的模型可以表示为：

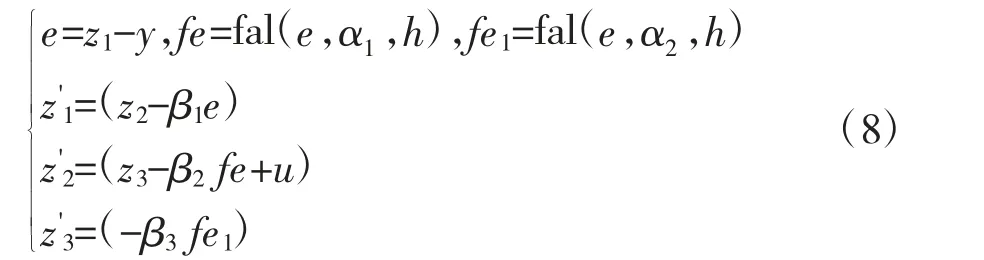
微分跟踪器TD，其数学模型为扩张状态观测器ESO，其数学模型为

非线性控制律NLSEF，其数学模型为

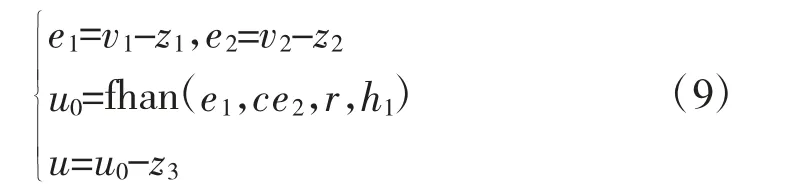
其中，v1为TD 提取的v（t）的过渡过程；v2为v（t）经过TD 所得的微分信号；h 为采样步长；r 为跟踪速度因子；z1，z2为y 的跟踪信号；z3为扰动估计值；α1，α2为非线性因子；δ 为滤波因子；β1，β2为ESO系数［5］。

对设计的二阶自抗扰控制进行参数调整后得到合适的参数，或应用时间尺度方式得到其他永磁同步电机的ADRC 参数［6］

h=0.01，b=1，c=0.1，r=10 000，h1=0.1，h0=0.01，r0=50 000，beta1=100，beta2=300，beta3=1 000，p=4，fai_f=0.071 45，B=2e-9，J=7.24e-4，L=0.01，Rs=2.875 8

2 改进自抗扰控制器

2.1 负载转矩观测器

在PMSM 数学模型中就可以计算负载转矩：

即负载转矩观测器的数学模型。

由上式可以得到计算负载转矩的仿真模型，如图1 所示。

图1 负载转矩观测器的仿真模型

当电机的参数阻尼系数B 和惯量J 不能很好地得到时，使用如下算法进行参数估计：

在永磁同步电机空载时，由式（5）可得

对一段时间t1 到t2 进行积分，以去掉导数项

两侧乘ωr

再定积分

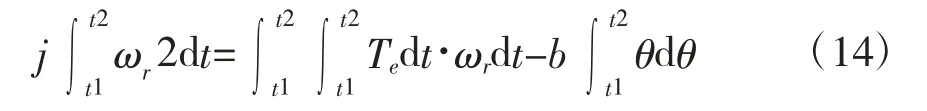
得到

其中

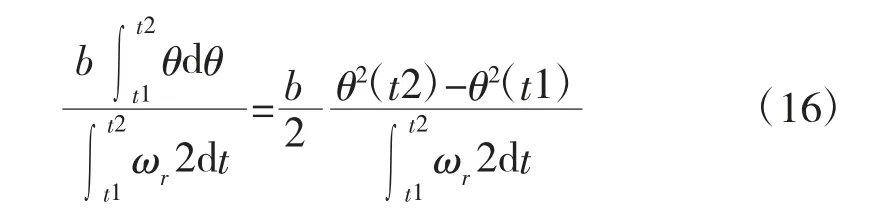
当t2 比t1 大的多时这一项趋近于0，这样就去掉了b 项

则

这样就得到了

2.2 前馈控制

与常见的闭环控制的系统模型相比，前馈控制系统是一种采用开环控制的系统。前馈控制的不变性原理包含动态不变性与稳态不变性［8-9］。一个比较典型的前馈开环控制的模型如图2 所示。系统包括控制通道和扰动通道。

图2 典型前馈控制模型

G1（s）：扰动通道传递函数；G2（s）：前馈控制器传递函数；G3（s）：控制通道传递函数；d（t）：可观测扰动；u（t）：控制输入；（t）：被控对象输出。

通过调整前馈控制器传递函数，抵消可观测扰动对最终输出的影响。

若使被控对象与干扰信号无关，可得：

对于永磁同步电机的运动方程：

代入

得到

所以

G2（s）为根据q 轴电流进行前馈控制的传递函数。

3 仿真模型设计

将负载转矩观测器和前馈控制传递函数模块与永磁同步电机的速度环二阶自抗扰控制器结合，输出q 轴电流的参考值。系统模型如下页图3所示。

图3 负载转矩观测器改进二阶自抗扰控制系统模型

4 仿真结果及分析

为验证改进ADRC 的PMSM 负载转矩补偿系统的性能，本文利用Simulink 对整个系统实现了仿真。

电机各个参数如下：定子电阻2.875 8 Ω，d、q 轴电感分别为Lq=Ld=0.01 mH，转动惯量J=0.008 5 kg·cm2，极对数p=4，额定转矩为5 N·m，转子磁通φf =0.174 5 Wb。给定转速1 000 rad/s。

图4 改进自抗扰控制器和二阶自抗扰控制器动态响应对比图

首先比较改进自抗扰控制器和二阶自抗扰控制器的动态性能，蓝色为改进二阶自抗扰控制器，黄色为二阶自抗扰控制器。

从图4 来看，两者的动态响应完全相同。

在不加入负载扰动模块时，因为没有外部扰动存在，负载扰动观测器没有发挥作用，改进二阶自抗扰控制器与二阶自抗扰控制器的基本控制量也完全一样，所以动态响应也完全相同。

说明在没有外部扰动的情况下，改进二阶自抗扰控制器与二阶自抗扰控制器具有相同的控制效果。

图5 改进自抗扰控制器和二阶自抗扰控制器负载扰动性能比较图

图5 是在1 s 突加2 N·m 负载时，改进二阶自抗扰控制器与二阶自抗扰控制器抗负载扰动性能的对比。蓝色为改进二阶自抗扰控制器，黄色为二阶自抗扰控制器。

从图5 中可以看出，改进二阶自抗扰控制器将原二阶自抗扰控制器对应的最大转速波动从1 500 r/min 减小至360 r/min。

虽然对象的模型发生了变化，但负载观测器估计出负载的变化，通过前馈控制对自抗扰控制器的性能进行了提升。说明负载转矩观测器改进的二阶ADRC 具有更强的抗负载能力。

下页图6 是加入随机扰动负载时，改进二阶自抗扰控制器与二阶自抗扰控制器稳态波动能力的对比。蓝色为改进二阶自抗扰控制器，黄色为二阶自抗扰控制器。

从图6 中可以看出，面对随机负载扰动，改进二阶自抗扰控制器将原二阶自抗扰控制器的波形变化减小了接近50 %，且在部分时段效果更好。

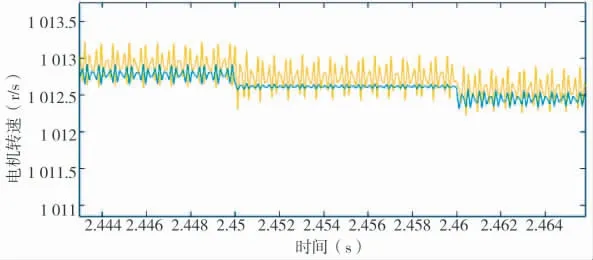
图6 改进自抗扰控制器和二阶自抗扰控制器对随机负载扰动的稳态能力

改进二阶自抗扰控制器具有更小的稳态波动。当存在外部负载扰动时，负载转矩观测器更好地估计了扰动并补偿控制量到矢量控制系统中，使改进的二阶自抗扰控制器稳态波动更小。

5 结论

本文将自抗扰和前馈控制、负载转矩观测器结合起来并应用于永磁同步电机控制转速环，设计负载转矩补偿通道，提升整体的抗负载扰动能力与动态稳定性。

仿真结果显示，改进自抗扰前馈补偿的永磁同步电机调速系统具有较好的动静态特性，系统鲁棒性也有所提升。