里程计辅助的高精度车载GNSS/INS组合导航系统

刘鹏飞

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081;2.中国电子科技集团公司 第五十四研究所，河北 石家庄 050081)

1 引 言

卫星导航系统(Global Navigation Satellite System,GNSS)具有全球性、全天候、精度高等优点，已广泛应用于车载组合导航系统中，但GNSS信号容易被遮挡和干扰，动态性能较差；捷联惯性导航系统(Strap-down Inertial Navigation System,SINS)不依赖于外界环境，可以完全自主地提供全面的导航信息，动态性能好、短时间内导航精度高，但其由于惯性测量单元(Inertial Measurement Unit,IMU)本身存在测量误差，导致导航系统的误差随时间累积，不利于长时间长距离的高精度导航[1-2]；将GNSS和INS进行组合构成组合导航系统，可实现优势互补，提高导航系统的精度和可靠性[3]。但是在城市隧道、高架桥下等长时间无GNSS信号的场景下，车载组合导航系统的精度会急剧下降，抗干扰能力和可靠性也无法得到保障。

因此，在没有GNSS信号的场景下，可以采用其他的导航传感器来辅助惯性导航系统，而易于车辆安装的里程计(Odometer,OD)则通过输出位置增量信息，利用航位推算(Dead-Reckon,DR)算法可实现完全自主导航，进一步抑制惯导系统长时间无GNSS信号场景下的误差发散，但是里程计本身受车辆安装位置、轮胎气压、轮胎磨损程度以及车辆载荷等因素影响，会直接导致标度因数误差和车辆安装误差等发生变化[4]，所以在里程计辅助的车载GNSS/INS组合导航系统里程计的初次安装使用前，必须对里程计的误差项进行标定和补偿[5-7]。文献[8]对设定已知路标点的传统里程计标定方法进行了详细介绍；文献[9]提出了一种基于运动学非完整约束的里程计参数在线辨识方法，取得了较好的测试结果。

航位推算的位置误差随着车辆行驶里程的增加而逐渐变大，所以在GNSS信号质量较好的路段，车载导航系统的组合模式应由DR/INS组合模式切换回GNSS/INS组合模式，进一步抑制由航位推算带来的位置误差积累。文献[10]提出了GPS/SINS/OD组合导航定位系统，采用联邦卡尔曼滤波对SINS进行误差估计并作反馈校正，通过仿真验证了该算法可有效抑制组合导航系统误差的发散，但该文献并没有在实际的动态跑车测试环境下进行算法的验证，也没有验证GNSS/INS模式和DR/INS模式自适应切换场景下的算法性能；文献[11]将里程计输出位置信息与惯导输出位置信息做差作为观测，将估计出的误差信息进行反馈校正，构成了紧组合导航系统，但是该系统在长时间导航下还是会存在航位推算误差累积的问题；文献[12-13]则是从GNSS/INS组合的角度对组合导航系统进行了介绍，并没有考虑当GNSS信号长时间失锁组合导航精度下降的问题。

本文提出一种里程计辅助的高精度车载GNSS/INS组合导航方法，组合滤波模式根据载车环境变化可在GNSS/INS组合模式和DR/INS组合模式间实现自适应切换，保证车载GNSS/INS组合导航系统在复杂路况下的高精度可靠定位。

2 组合导航系统设计

组合导航系统原理图如图1所示，在GNSS信号质量良好，卫导接收机可提供可靠导航信息时，自适应组合滤波器则利用卫导提供的位置、速度信息作为外部观测量对组合滤波器进行量测更新，此时的航位推算模块不工作，自适应组合滤波器将更新后的误差估计值反馈回惯性导航系统，对惯性导航系统进行误差修正，同时组合导航滤波器输出最优的组合导航信息；当复杂路况下卫导信号不可用时，航位推算模块根据上一时刻惯导提供的导航信息进行航位推算，自适应组合滤波器则根据航位推算提供的位置信息作为外部观测量对组合滤波器进行量测更新，自适应组合滤波器将更新后的位置误差估计值反馈回航位推算模块中，对航位推算模块进行位置修正，同时组合导航滤波器输出最优的组合导航信息；组合导航滤波器只需根据卫导是否定位，即可在GNSS/INS和DR/INS组合模式间快速切换，保证组合导航系统高可靠连续性的高精度定位。

图1 里程计辅助的高精度车载GNSS/INS组合导航系统原理图Fig.1 Block diagram of high-precision vehicle GNSS/INS integrated navigation system aided by odometer

3 组合导航系统误差分析

选取东北天地理坐标系作为导航坐标系，记为n系；惯性坐标系记为i系；假设里程计坐标系与车体坐标系重合，记为m系，ox轴沿车体横轴方向指向右方，oy轴沿车体纵轴指向正前方，oz轴垂直于地面向上，和ox轴、oy轴构成右手直角坐标系，即构成一个右-前-上坐标系；载体坐标系，即惯导坐标系记为b系，坐标轴向定义与车体坐标系一致；文中涉及到的导航坐标系示意图图2所示。

图2 导航坐标系示意图Fig.2 Diagram of Navigation coordinate system

3.1 捷联惯导系统(SINS)误差分析

参照文献[8]列出SINS的位置误差方程、速度误差方程和姿态误差方程如式(1)：

(1)

3.2 航位推算(DR)位置误差分析

首先考虑里程计标度因数误差δKD，给出DR速度误差方程：

(2)

在不考虑里程计安装误差角的情况下，里程计航位推算位置误差方程与捷联惯导系统位置误差方程一致，如式(3)所示：

(3)

其中：D表示航位推算系统误差。

将式(2)代入到式(3)可得含里程计标度因数误差的位置误差方程：

(4)

然后在考虑里程计安装误差角的情况下推导位置误差方程。

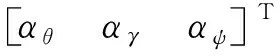
(5)

航位推算误差源主要包括：里程计平台失准角φD、里程计安装偏差角αθ和αψ中未能完全补偿的剩余俯仰安装误差角δαθ和方位安装误差角δαψ以及里程计标度因数误差δKD，安装误差角和安装偏差角间的关系如式(6)所示：

(6)

(7)

对式(7)进一步处理，忽略各误差项二阶和高阶小量，可得：

(8)

(9)

(10)

矩阵Ma可进一步简化为常值矩阵：

(11)

最终得到的位置误差方程：

(12)

至此，包括里程计标度因数误差、俯仰安装误差角以及方位安装误差角的航位推算位置误差方程已得到。

4 组合导航系统滤波器设计

本节首先给出里程计辅助的GNSS/INS组合导航系统滤波器设计的具体过程，并简单描述了经典Kalman滤波的更新过程，然后对航位推算算法的位置更新算法和姿态更新算法进行介绍。

4.1 组合导航系统滤波器设计

状态方程中，选取捷联惯导系统误差中的姿态误差φ、速度误差δv、位置误差δp、陀螺仪漂移εb、加速度计常值偏置b以及航位推算误差中航位推算位置误差δpD、里程计标度因数误差δK、俯仰安装误差角δαθ以及方位安装误差角δαψ作为滤波器的状态量，共计21维，具体表示如式(13)：

X=

(13)

(14)

其中：F为状态转移矩阵，G为噪声分配矩阵，W为系统状态噪声阵；结合式(1)、式(12)，状态转移矩阵F的表达式如式(15)所示：

(15)

由GNSS接收机构成的观测方程如式(16)所示：

(16)

针对里程计航位推算模块，将捷联惯导解算的位置与里程计航位推算的位置之差作为系统观测量，则由里程计航位推算模块构成的观测方程如式(17)所示：

δp-δpD=HDX+VD

HD=[03×6I3×303×6-I3×303×3]T.

(17)

至此，由里程计辅助的GNSS/INS组合导航系统滤波器的状态方程和量测方程推导完成。

进一步将组合导航系统状态方程(14)和观测方程(16)、方程(17)进行离散化为式(18)：

Xk=Φk,k-1Xk-1+Γk,k-1Wk-1

Zk=HkXk+Vk,

(18)

其中：Φk,k-1为系统离散化后的状态转移矩阵，Γk,k-1为离散化后的噪声分配矩阵。Xk与Xk-1依次代表系统在k时刻和k-1时刻的状态量，Wk-1代表系统的状态噪声，Vk代表系统的观测噪声。

式(18)的具体实现过程可使用经典Kalman滤波的更新过程表示，如式(19)～式(25)所示：

状态一步预测方程：

(19)

状态估计：

(20)

一步预测误差方差阵：

(21)

滤波增益矩阵:

(22)

估计误差方差阵：

(23)

滤波增益矩阵又可以进一步写成：

(24)

估计误差方差阵又可以进一步写成：

Pk=[I-KkHk]Pk,k-1.

(25)

4.2 航位推算算法

航位推算过程主要是利用里程信息、姿态以及航向信息来推算载车相对于初始点的相对位置，航位推算过程主要包括位置更新和姿态更新。

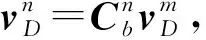
与捷联惯导解算的位置更新微分方程类似，可以列出航位推算的位置更新微分方程：

(26)

根据式(26)即可得到航位推算的数字更新算法：

(27)

5 车载试验验证

车载试验装置由高精度光纤GNSS/INS组合导航系统、里程计、流动站GNSS接收机、基准站GNSS接收机、GNSS接收天线以及GNSS高精度后处理软件等组成，其中各模块的技术指标如表1所示。

表1 车载组合导航系统技术指标列表

Tab.1 Technical indicators for vehicle integrated navigation system

技术指标动态范围光纤陀螺仪零偏稳定性:≤0.01 (°)/h±300 (°)/s石英加速度计偏置稳定性:≤50 μg±6 gGNSS流动站/基准站接收机定位精度:10 m速度限制:≤515 m/s里程计标度因数误差:≤0.2%无限制GNSS高精度后处理软件定位精度:≤5 cm无限制

光纤惯组和GNSS组合导航接收机均固连在车辆行李架上置于车顶，里程计安装于测试车辆右后轮的转轴上。测试开始前，在一大约4 km的平直路段上使用传统里程计标定方法对里程计误差进行标定，标定出里程计标度因数误差为0.15%，俯仰安装误差角为2.14°，方位安装误差角为1.06°，将标定出的里程计误差参数装订到车载组合导航系统中。

基准站GNSS接收机天线架设在单位四楼楼顶的标准已知点上，使用GNSS后处理的高精度位置信息作为测试的位置参考信息。图3为里程计在车辆的安装图、惯组和组合导航接收机在车辆行李架的安装图以及基准站接收机和基准站天线在楼顶的安装图。测试时使用功分器将车顶的GNSS接收天线分别和流动站GNSS接收机和GNSS/INS组合导航接收机连接。

图3 车载组合导航系统安装图Fig.3 Installation diagram of vehicle GNSS/INS integrated navigation system

为进一步模拟车辆在隧道等遮挡环境下的组合导航系统定位精度，在车辆行进过程中切断GNSS/INS组合导航接收机的天线信号，时间大约为7 min，行驶里程大约为7 km，分两个路段切断组合导航接收机天线信号，时刻大约从405～800 s和1 010～1 400 s，为进一步评估有里程计辅助下的组合导航系统位置精度，分别进行两次重复试验，试验1为有里程计辅助下的车载跑车试验，试验2为无里程计辅助下的车载跑车试验，两次重复试验车辆的行驶轨迹和参考基准轨迹分别如图4、图5所示，位置误差如图6和图8所示，速度误差如图7、图9所示。

图4 试验1-车辆行驶轨迹Fig.4 Test 1-Vehicle trajectory of integrated navigation system

由图6、图8可以看出，在无卫导信号的两次GNSS信号中断时刻，有里程计辅助的组合导航系统，单个方向位置误差最大值也未超过8 m，同时可以看出当卫导信号恢复后，位置误差能够很快收敛到正常水平；而无里程计辅助的组合导航系统，经度误差最大值将近160 m；由图7、图9可以看出，在无卫导信号的两次GNSS信号中断时刻，有里程计辅助的组合导航系统，单方向的速度误差最大值也未超过0.1 m/s；而无里程计辅助的组合导航系统，天向速度误差最大，最大值达到了0.5 m/s。明显可以看出有里程计辅助下组合导航系统精度要优于无里程计辅助下的组合导航系统精度。

图5 试验2-车辆行驶轨迹Fig.5 Test 2-Vehicle trajectory of integrated navigation system

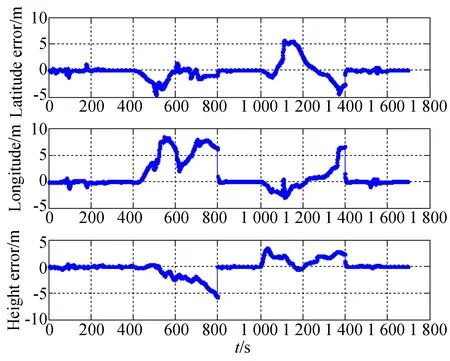
图6 有里程计辅助下的位置误差Fig.6 Position error aided by odometer

图7 有里程计辅助下的速度误差Fig.7 Velocity error aided by odometer

图8 无里程计辅助下的位置误差Fig.8 Position error without odometer assistance

图9 无里程计辅助下的速度误差Fig.9 Velocity error without odometer assistance

从表2中也可以看出，有里程计辅助的组合导航系统位置误差在3 m以内；而无里程计辅助的组合导航系统位置误差达到了42.4 m，远大于有里程计辅助的定位误差。

表2 位置误差统计表

图10 自主导航系统水平位置误差Fig.10 Autonomous navigation system horizontal position error

试验最后给出了高精度光纤惯性导航系统只在里程计辅助下的自主导航系统精度，试验路段同试验1、试验2的测试路段，整个测试路段共计31.2 km，水平位置误差如图10所示，可以看出整个测试过程中单方向的位置误差最大值不超过20 m，精度统计值约为0.08×D(D为车辆行驶里程)，高于0.01 °/h的光纤惯导系统自主导航系统0.1%D的常规指标要求。

6 结 论

针对城市隧道、偏远山区等复杂路况，GNSS信号遮挡较严重或长时间无GNSS信号的场景下，车载GNSS/INS组合导航系统精度下降的问题，提出一种里程计辅助的高精度车载GNSS/INS组合导航方法，在考虑里程计标度因数误差、里程计安装误差角的情况下，将航位推算位置误差、里程计标度因数误差、安装误差角列入传统的组合导航滤波器的状态量中，建立了组合导航滤波器的状态方程和量测方程，实现了GNSS/INS组合模式和DR/INS组合模式间的自动切换，在DR/INS组合模式下，使用惯导解算的位置与航位推算的位置之差作为滤波器的观测值，进行滤波器的量测更新。整个跑车过程中位置误差在3 m以内，进一步验证里程计辅助下的车载组合导航系统的正确性。