全视场外差短相干形貌测量技术
吕 彤,张文喜*,吕笑宇,李 杨,伍 洲,孔新新
(1.中国科学院 光电研究院 计算光学成像技术重点实验室,北京 100094;2.中国科学院大学 光电学院,北京 100094)
1 引 言
物体的三维形貌能够全面、真实地反映尺寸、缺陷等信息,是表征物体几何信息的重要参数。三维形貌测量技术[1-6]一直是测量、计量和工业检测等领域的研究热点。高精度三维轮廓测量技术主要可分为接触法和非接触法[7-11]。接触法使用机械探针对物体的表面进行接触测量,并利用传感器将高度信息转换为电信号,通过处理电信号来获得物体的表面三维信息,具有精度高、数据反演简单等优点,缺点是易损坏待测目标表面、空间分辨率低和效率低。光学测量具有精度高、速度快、无接触和无破坏性等优点,如白光干涉法、计算全息法、投影法和共焦法等[12-15]。其中,利用白光短相干特性的白光干涉测量技术,广泛应用于显微高精度测量领域。
白光干涉测量技术以钨灯、LED灯等作为光源,其光谱较宽、相干长度短,能够利用定位零光程差位置进行精密测量[16-22]。该技术具有测量精度高、可溯源等优点,缺点是采样间隔小、数据采集时间长、处理算法复杂,难以满足工业检测领域实时的测量需求。将白光干涉测量系统的白光光源转换为短相干光源,同样能够进行三维测量。由于短相干光源的相干长度约为200 μm左右,大于传统白光光源,其测量精度相对于传统白光光源略有降低。但利用短相干光源相干长度较长的特点,测量时载物台移动的步长大幅增加,从而大幅提升测量效率。
本文在简要介绍白光测量与短相干光测量区别的基础上,提出了一种基于全视场外差短相干测量的方案,采用全视场外差技术与短相干测量技术相结合的方法,通过简单的数字运算,能够较精确地定位干涉零光程差的位置。在保障测量精度的同时,大幅降低零光程差位置的计算难度,有效提高测量效率。该技术具有微米级测量精度、秒级测量时间,在对效率要求较高的工业检测领域具有一定的应用前景。
2 全视场外差短相干测量原理
2.1 设计思想
传统白光干涉测量把宽谱段光源光束分成参考光束与测量光束。两束光分别由参考镜与待测物表面反射进入探测器干涉。通过精确移动待测物,改变测量光束的光程差,进而可以得到待测物每一点的干涉条纹。通过分析干涉条纹零光程差的位置,能够给出待测物上每一点的距离差,实现高精度测量。图1给出了白光干涉测量空间两点通过零光程位置进行高度差测量的示意图。由于白光干涉图为调制图,无法直接获取零光程差的位置,因此零光程差点的位置通常采用权重法、傅里叶分析法和相位法等[23-30]算法获得。但以上方法对采样步长具有严格的限制,采样时间长、计算量大,难以满足准实时性的检测需求。
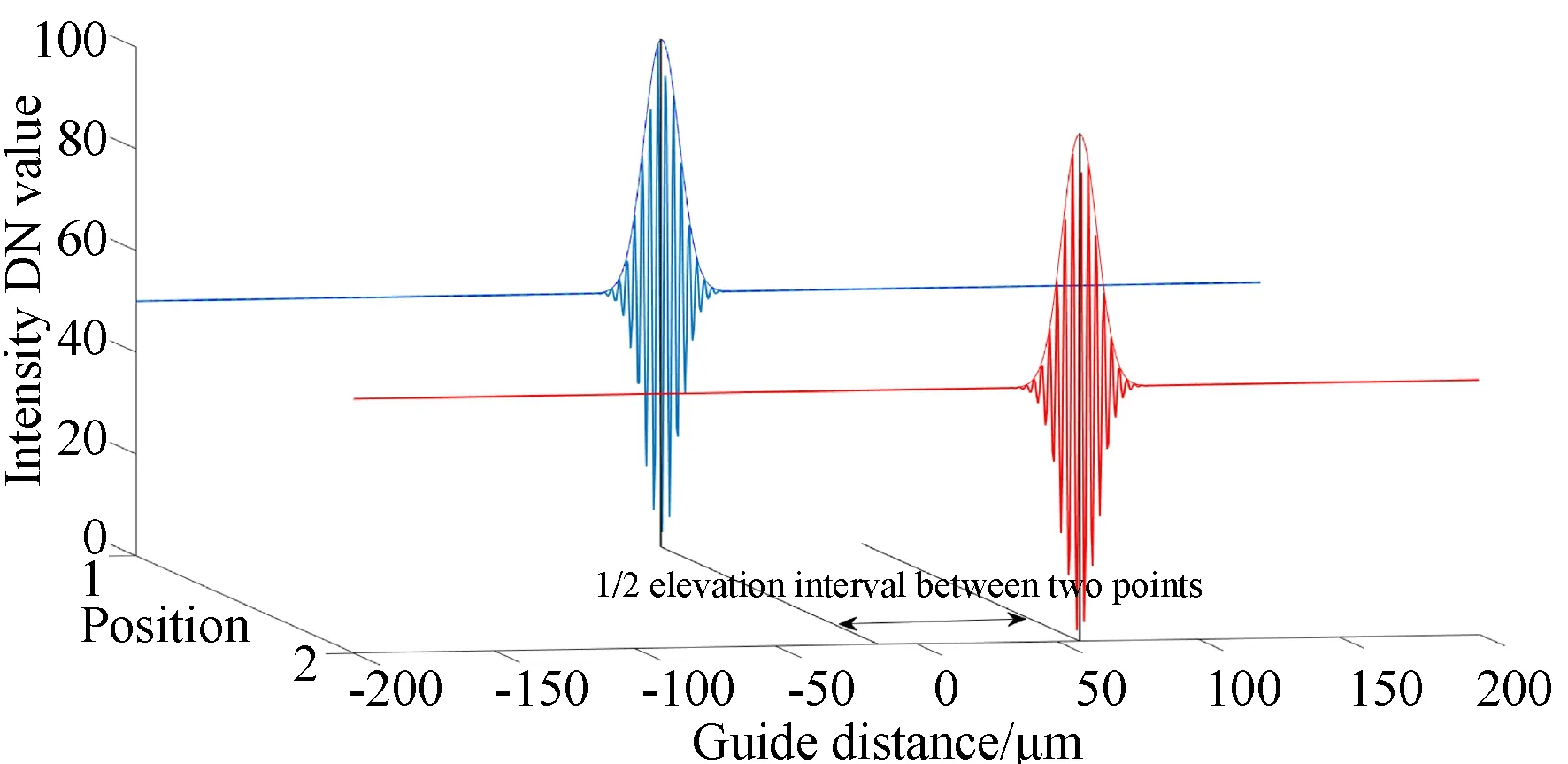
图1 白光干涉测量原理Fig.1 Principle of white light interferometry
短相干光源测量原理与白光干涉测量原理基本相同,图2给出了短相干光源与白光光源大步长采样的干涉曲线(彩图见期刊电子版)。红色为短相干光源对应的干涉曲线,蓝色为白光光源对应的干涉曲线,采样步长为1 μm。从图中可以看出,在光源能量相同的情况下,白光干涉对比度比短相干干涉对比度高,但短相干光源的干涉区域较宽,在欠采样情况下,短相干光源零光程的定位精度相对较高。因此在测量精度要求不高,对测量效率要求较高的领域,可以采用短相干光源干涉测量技术。
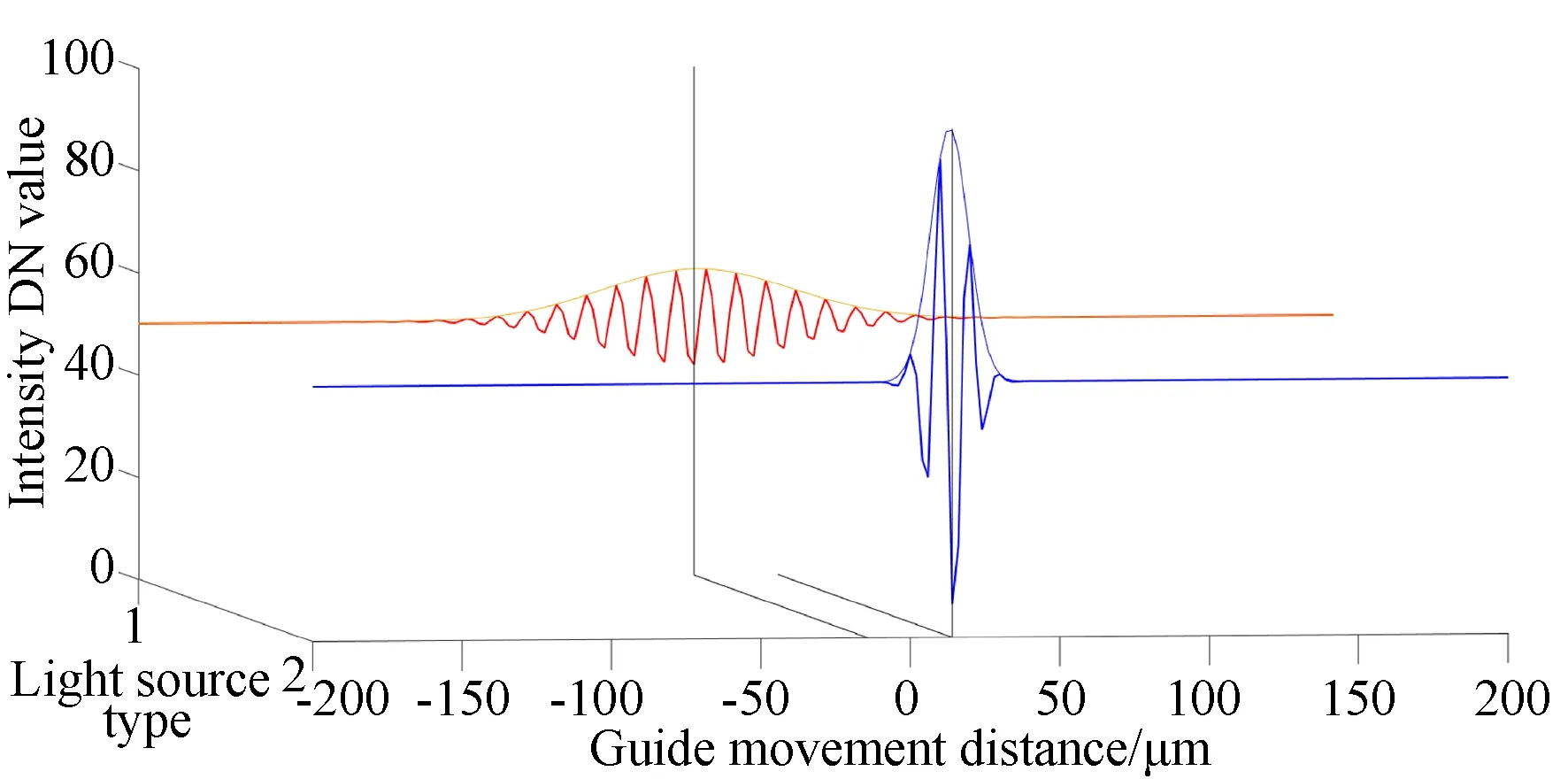
图2 短相干光源与白光光源干涉曲线比较Fig.2 Comparison of interference curves between short coherent light source and white light source
与白光光源干涉测量数据的反演算法相同,短相干光源干涉测量可以直接采用白光干涉测量的权重法或傅里叶变换法。其中,权重法简单高效,但精度较差。傅里叶变换法精度较高,但计算量较大、数据反演效率低,难以满足较高的实时性要求。本文提出采用双频短相干光源的测量方案,能够高效率获取干涉曲线的轮廓,再采用权重法定位零光程差位置。在保证测量精度的同时,有效减小数据的分析时间,提高测量效率。
2.2 全视场外差短相干测量基本原理
全视场外差短相干测量技术是一种利用短相干光特性进行精密位置测量的技术,该技术通过外差调制和解调获取短相干光干涉的轮廓曲线,提高数据反演效率。图3为全视场外差短相干测量的原理图,该系统由双频短相干光源模块和干涉测量模块组成。双频短相干光源主要由短相干光源、声光移频器、偏振分光棱镜、角锥和光纤耦合镜等组成。短相干光源发出的光束经偏振分光棱镜分成相互垂直的两束激光,两束激光分别经过声光移频器移频后,再经过角锥和偏振分光棱镜合束,最后耦合到单模保偏光纤中。两束激光的光程差相等,两个移频器的频率差为Δf。最终形成偏振方向相互垂直的双频短相干光源,作为测量系统的光源。干涉测量模块采用偏振分光的Linnik干涉仪结构,振动方向正交的双频短相干光源经光纤头出射进入干涉模块。探测光束由偏振分光镜3透射,再经1/4波片、透镜照射到被测面,经被测面反射后,再经1/4波片、偏振分光棱镜3和偏振片进入探测器。参考光经偏振分光棱镜3反射,照射到参考面上,再经参考面反射回探测器。面阵探测器获取探测光束和参考光束的干涉图。
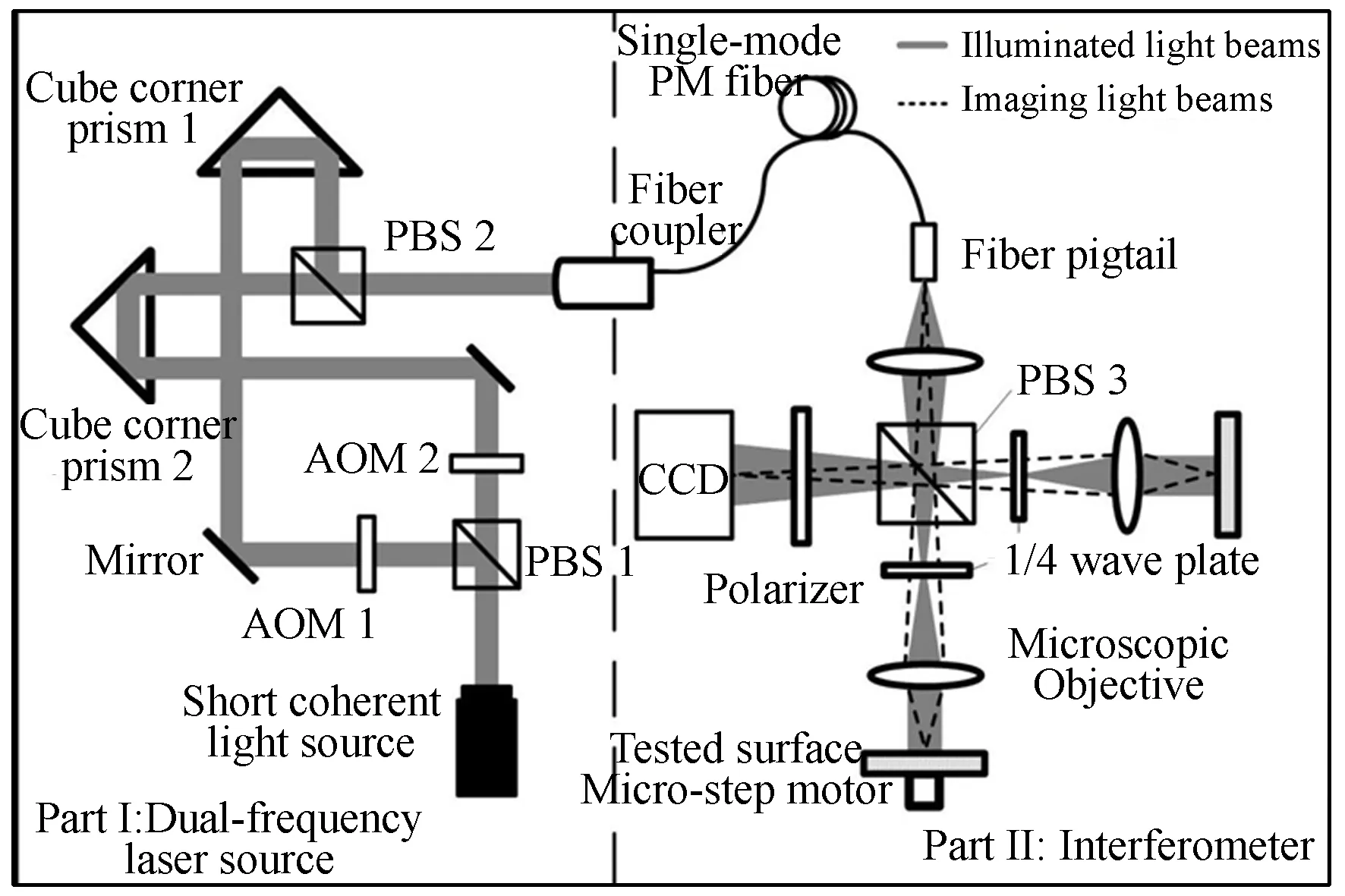
图3 全视场外差短相干测量系统原理Fig.3 Principle diagram of full-field heterodyne short coherent measurement system
两束光经过的光程完全对称,当测量面的高度与参考面的高度相等时,两束光的初始相位相等,形成零光程干涉位置。当测量面高度与参考面高度存在高度差h时,通过载物台的运动配合数据反演算法,能够对零光程差位置进行定位,从而得到物体的高度。其测量的基本原理与传统白光干涉测量相同,不考虑两束光存在频差时,探测器得到的干涉强度为:
(1)
其中:E1,E2,k,lc,ξ分别为测量光束到达探测器的振幅、参考光束到达探测器的振幅、光束的波数、相干长度和光谱系数。两束光存在Δf的频差时,干涉强度可以表示为:
I(h,t)=
(2)
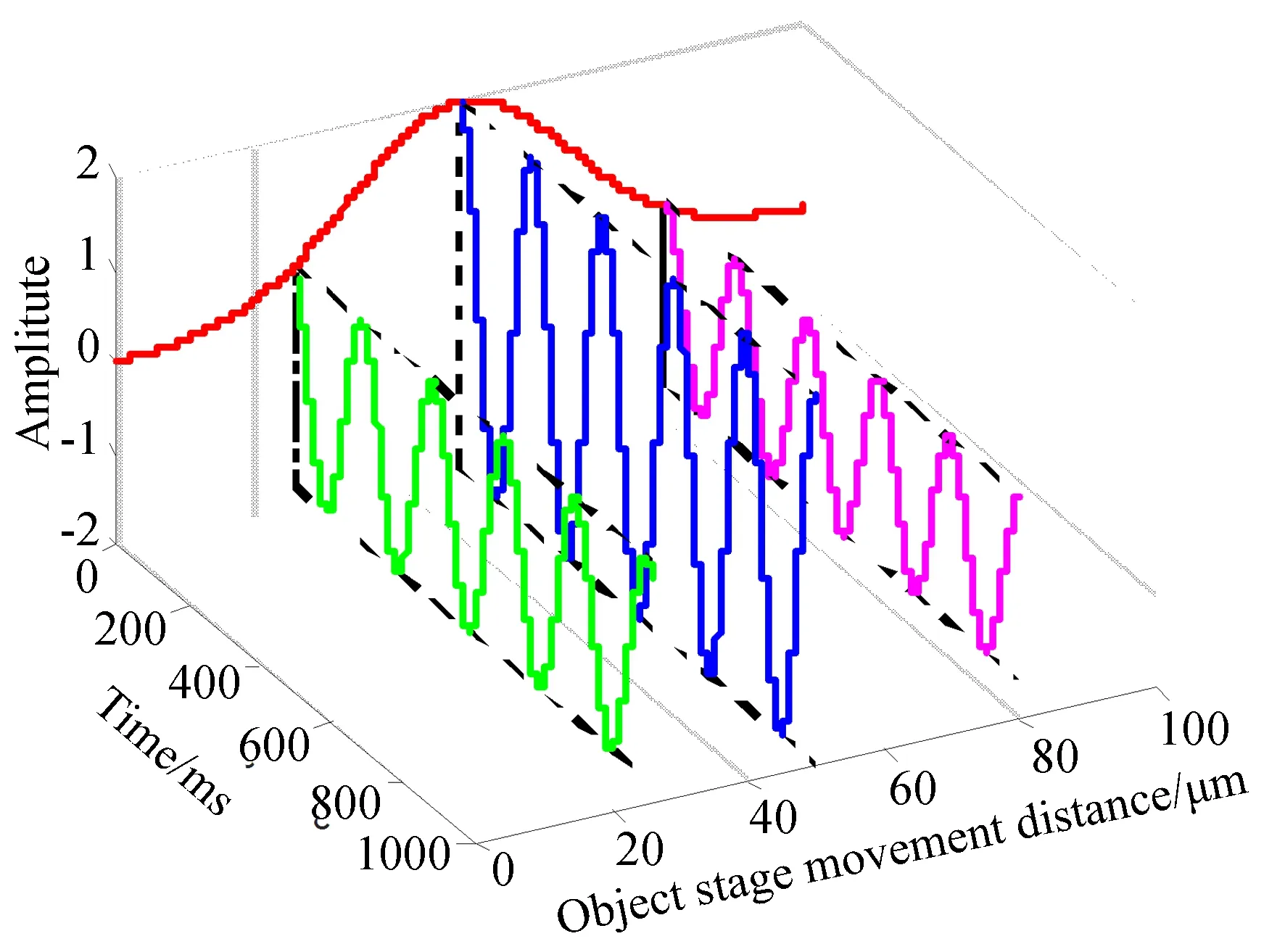
图4 全视场外差测量数据分析原理Fig.4 Principle for full-field heterodyne measurement data analysis
图4给出了全视场外差探测系统载物台运动到不同位置时,在空间某点探测到的数据。从图4可以得到,不考虑直流分量,载物台运动到某个位置时,该点可以探测到正弦曲线,进而获得该位置的正弦曲线振幅。通过拟合所有运动位置的信号振幅就可以获取该点的干涉曲线包络,且包络曲线为高斯曲线。当探测器帧频fccd=4Δf时:
(3)
I(h)=
(4)
从公式(4)可以看出,载物台每运动到一个位置,探测器连续采集4幅图。经简单运算就可以得到干涉曲线的高斯包络。曲线的形状仅与光源特性和两束光的光程差相关。利用高斯包络的顶点位置,能够测量任意两点的高度差。
2.3 数据反演
公式(4)给出了测量值与高度值之间的关系,高度值h可以通过重心法得到,即有:
(5)
其中:h为对应像素点零光程差位置,i为运动次数,δh为单次运动位移。相邻两包络间峰峰位置的距离差即为两个像素点间的高度差。随着载物台运动次数的增加,将被测样品所有的零光程差位置全部获取。此时,被测样品表面三维形貌测量完成。该方案不仅数据反演算法简单,且包络曲线不含直流分量,因此能够有效抑制直流分量引入的误差,提高测量精度。
3 测量实验与结果
为了验证该方案测量表面轮廓的可行性,搭建如图5所示的实验系统,短相干光源的中心波长为635 nm,相干长度约为190 μm。两束激光经两个移频器移频后,频率差为5 Hz,探测器的帧频为20 frame/s。载物台采用微型步进电机(PI-N565),单次步进距离为5 μm,光程差为10 μm 。

图5 全视场外差短相干形貌测量实验系统Fig.5 Experimental system of full-field heterodyne short coherent topography measurement technology
选用10 μm的台阶进行实验验证。图6给出了载物台运动到某一位置,台阶实拍的一个周期的4幅干涉图。
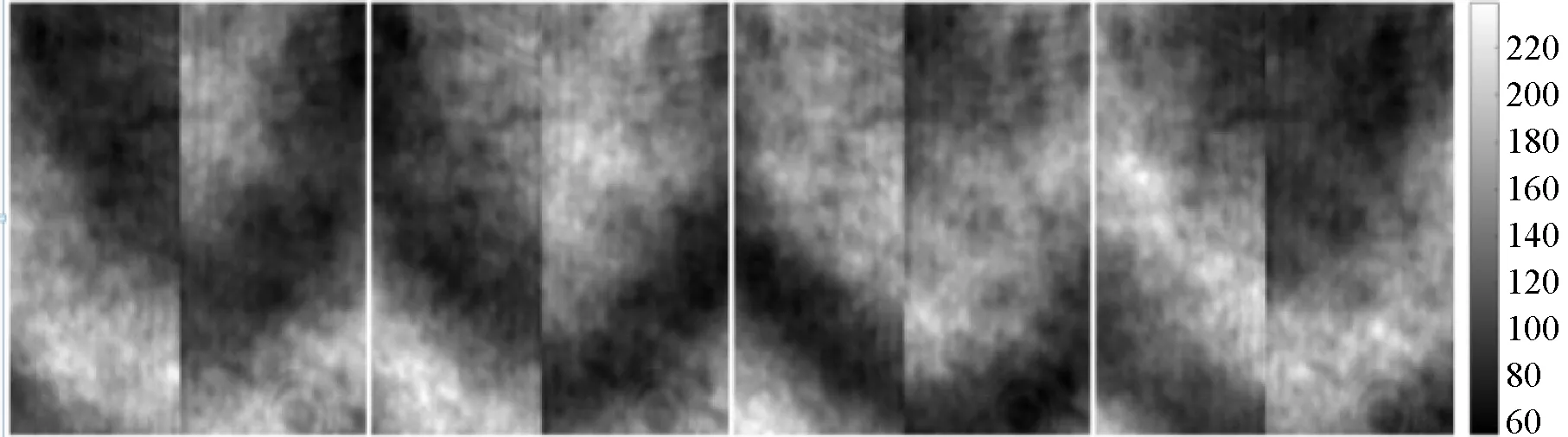
图6 台阶实拍干涉图Fig.6 Interferogram of step
图7给出了台阶坐标为(100,100)的点处,载物台分别运动到80,105和120 μm时,探测器探测得到的干涉曲线。可以看出,干涉曲线具有很好的正弦周期性,且不同位置的正弦曲线的振幅不同。周期为200 ms,与外差频率5 Hz相对应。
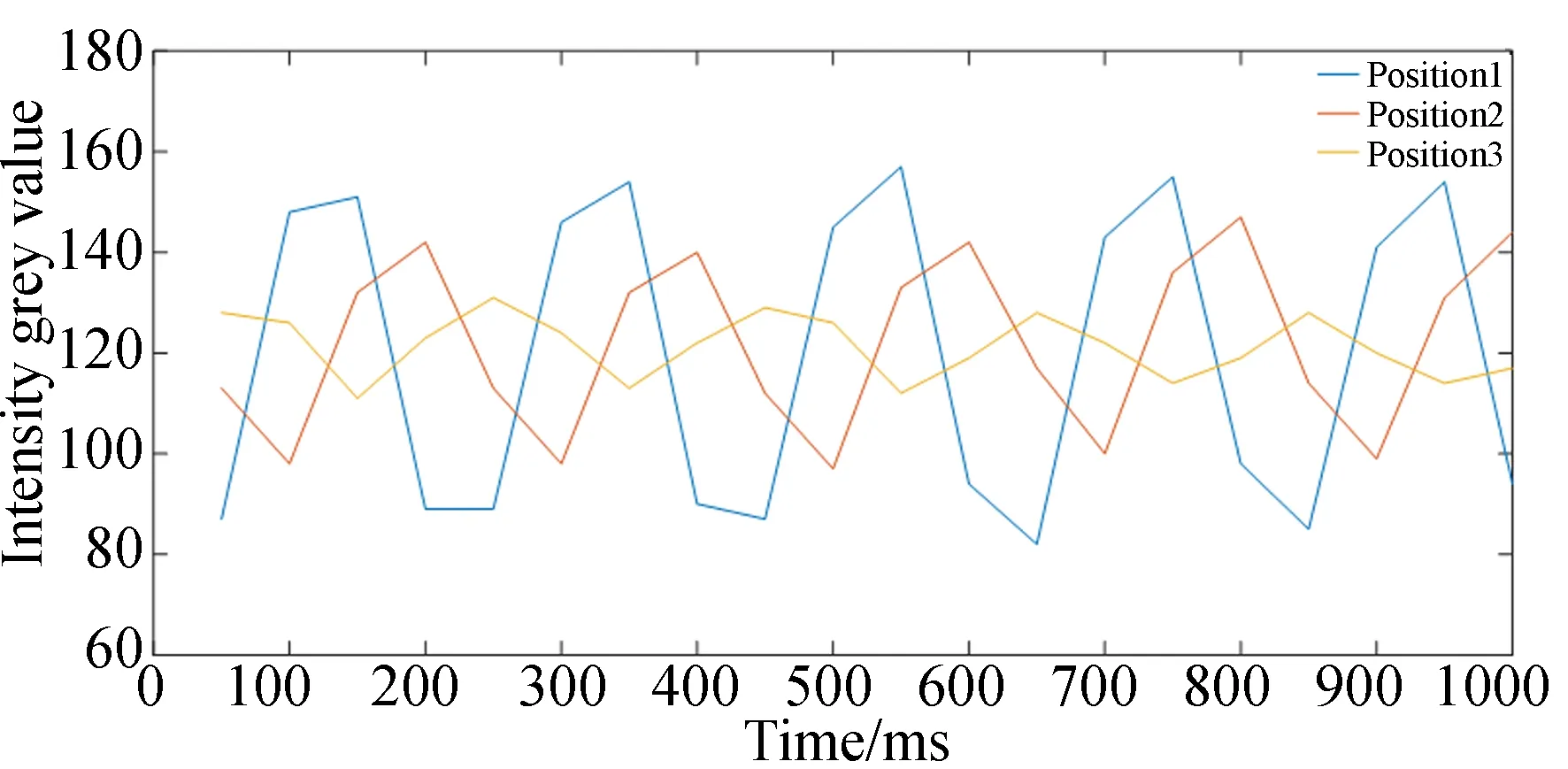
图7 不同载物台位置处的单点干涉曲线Fig.7 Interference curves with different stage positions at the same point
图8给出了空间位置(100,100)的采样点,在载物台不同位置处,由公式(4)拟合得到的正弦曲线振幅的分布,即白光测量对应的轮廓曲线。通过对轮廓曲线进行高斯拟合,表明其轮廓曲线为高斯曲线,数据质量较好。
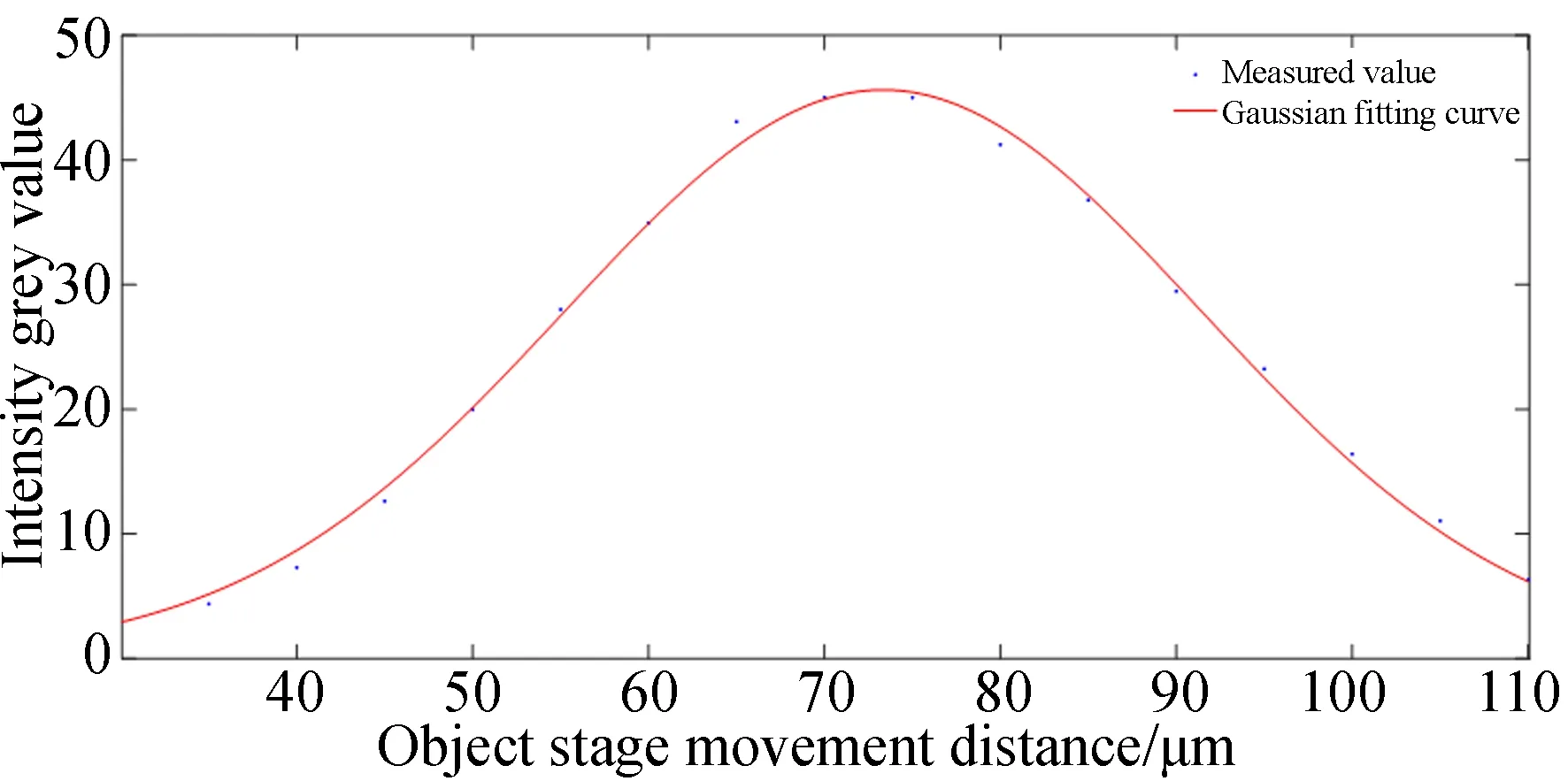
图8 实拍数据的高斯拟合结果Fig.8 Gaussian fitting results of detection data
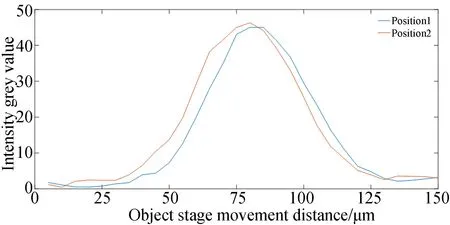
图9 不同位置处探测的轮廓曲线Fig.9 Contour curves detected at different positions
图9给出了坐标(80,100),(100,100)两点实测的轮廓曲线,两点分布在台阶的上下位置处。两点轮廓曲线均为高斯曲线,随着载物台运动的位置不同,两曲线错开。采用公式(5)计算零光程差对应的位置差为9.26 μm。
图10为采用上述测量方案得到的台阶三维形貌。图10(a)为台阶的三维轮廓,可以看出高度为10 μm的台阶通过该测量方法能够清晰分辨。图10(b)为位于台阶中间处提取出的一条直线的测量结果。台阶上高度相同位置测量的PV值小于2 μm,上台阶高度均值与下台阶高度均值的差约为9.7 μm,上下台阶的均值偏差约为0.3 μm。实验表明,采用该方法的测量精度优于2 μm。通过数据分析,误差主要来源于环境振动、污点衍射和显微物镜的像差。后续可以通过进一步优化设计提高系统的测量精度。当探测器采用1 024×1 024 pixel,被测物体高度小于300 μm时,系统测量时间小于10 s,可以实现较高精度的快速测量。通过优化移频器频差和探测器帧频,能够进一步提高系统的测量速度。
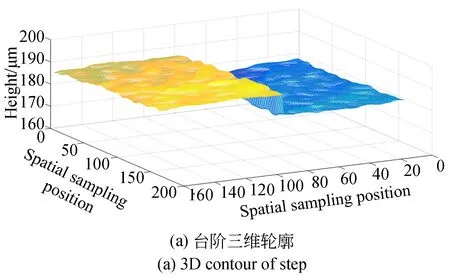
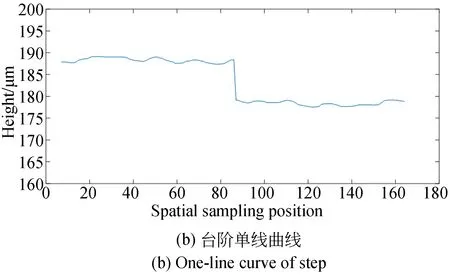
图10 台阶三维测量结果Fig.10 Three-dimensional measurement results of step
针对集成电路检测的需求,对集成电路的焊锡高度进行了测量,结果如图11所示。根据结果可以判断图中上方中间位置的焊锡为漏焊,证明采用该方法能够快速准确地判别缺陷,提高检测的效率和准确度。
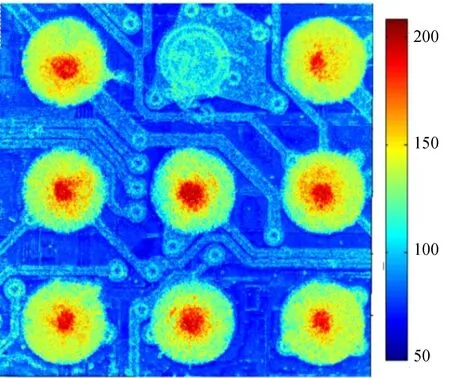
图11 集成电路实测结果Fig.11 Test results of integrated circuit
4 结 论
本文针对微米量级精度、秒级速度的检测需求,提出了全视场外差短相干形貌测量方案。该方案采用短相干光源实现大步长测量;采用全视场外差技术,实现干涉轮廓的快速反演,在抑制振动、直流噪声对测量精度影响的同时,提高数据反演的速度。搭建了实验验证系统,并对该测量方案进行了验证。实验结果表明:全视场外差短相干形貌测量技术的测量精度优于2 μm,可以通过进一步优化系统设计实现亚微米精度的测量;当探测器采用1 024×1 024 pixel,被测物体高度小于300 μm时,测量时间小于10 s,后续通过进一步优化,测量时间能够小于5 s。
相对于传统白光干涉测量,该方案具有算法简单、测量速度快等优势,但测量精度比传统白光测量方案低。相对传统结构光测量,该方案具有测量精度高、算法简单高效等优势,但不适合对高度差较大的目标测量。
在对测量速度要求较快、高度差较小和测量精度要求较高的检测领域,如集成电路焊锡检测等,采用该技术方案能够兼顾测量精度和测量速度,在微米量级工业检测领域具有一定的应用前景。

