基于天体运动更新机制的改进樽海鞘群算法

张文彬

(上海电力大学 自动化工程学院, 上海 200090)

樽海鞘群算法(Salp Swarm Algorithm,SSA)是2017年由MIRJALILI S等人[1]提出的一种新的智能算法。作为一种元启发式算法,SSA具有收敛速度快、设定参数少、简单易懂等优点,但也存在易陷入局部极值点、收敛精度不高等问题。目前,已有学者对该算法进行了改进并应用于相关研究。文献[2]引入了评估移动策略来增强算法的开发能力,并成功用于永磁同步电机的多参数辨识;文献[3]通过引入levy飞行机制来提高算法的全局搜索能力,并用于多阈值图像分割时的优化;文献[4]结合了混沌精英质心拉伸机制,有效地提高了SSA的收敛速度和收敛精度;文献[5]用Tent映射来初始化种群个体,并在食物源的位置中加入“疯狂”算子,提高了算法的开发能力。本文在SSA中引入天体运动算子来提高算 法的开发能力,并通过7个常用的算法测试函数验证改进算法的有效性。

1 樽海鞘群算法

1.1 基本原理

SSA的思想来源于樽海鞘聚集成一条链式的行为,即前后个体之间相互影响。将樽海鞘群中的个体划分为领导者和追随者,其中领导者在链的前端,对周围的环境有更好的判断。SSA的具体运算步骤如下[6]。

1.1.1 种群的随机初始化

设种群总数为N,其中领导者个数为Nl,追随者个数为Nf,解空间维数为D维,搜索空间的上限和下限分别为:ub=[ub1ub2ub3…ubD]和lb=[lb1lb2lb3…lbD],那么樽海鞘个体的位置可以表示为xi=[x1x2x3…xD]。

1.1.2 领导者的位置更新

对第i个领导者在第j维上的位置进行更新,表达式为

(1)

(2)

式中:Fj——目标食物的位置;

c2,c3——随机产生的数,范围均为[0,1];

t,tmax——当前迭代次数和最大迭代次数。

参数c1的值对于算法的开发和探索能力的平衡起着至关重要的作用。由式(2)可以看出c1的值由2递减到0。

1.1.3 追随者的位置更新

对第i个追随者在第j维上的位置进行更新,表达式为

(3)

式中:a——加速度;

t0——时间;

v0——初始速度。

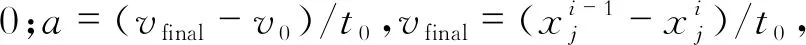
(4)

1.2 算法改进

天体运动更新的思想来自于天体物理学中行星绕太阳运动的轨迹[7]。本文将这一思想与SSA结合,得到天体运动更新的樽海鞘群算法(Astrophysics-inspired Salp Swarm Algorithm,ASSA)。其具体改进方法如下。

从N个种群中随机选择k个樽海鞘个体,让这k个个体围绕当前种群中最优的个体来更新位置,其更新表达式为

Yi,new=Ybest+Ri,bestU(-2,2)

(5)

式中:Yi,new——被选择的个体更新后的位置;

Ybest——当前最优个体;

Ri,best——个体i与最优个体间的距离;

U(-2,2)——区间[-2,2]内的随机数,与参数c1的变化相对应。

同时,最优个体也更新其自身位置,更新公式为

Ybest,new=YbestU(-2,2)

(6)

将更新后的位置与原位置相比,选择适应度较好的作为最终更新位置,即

(7)

改进后的樽海鞘群算法流程如图1所示。

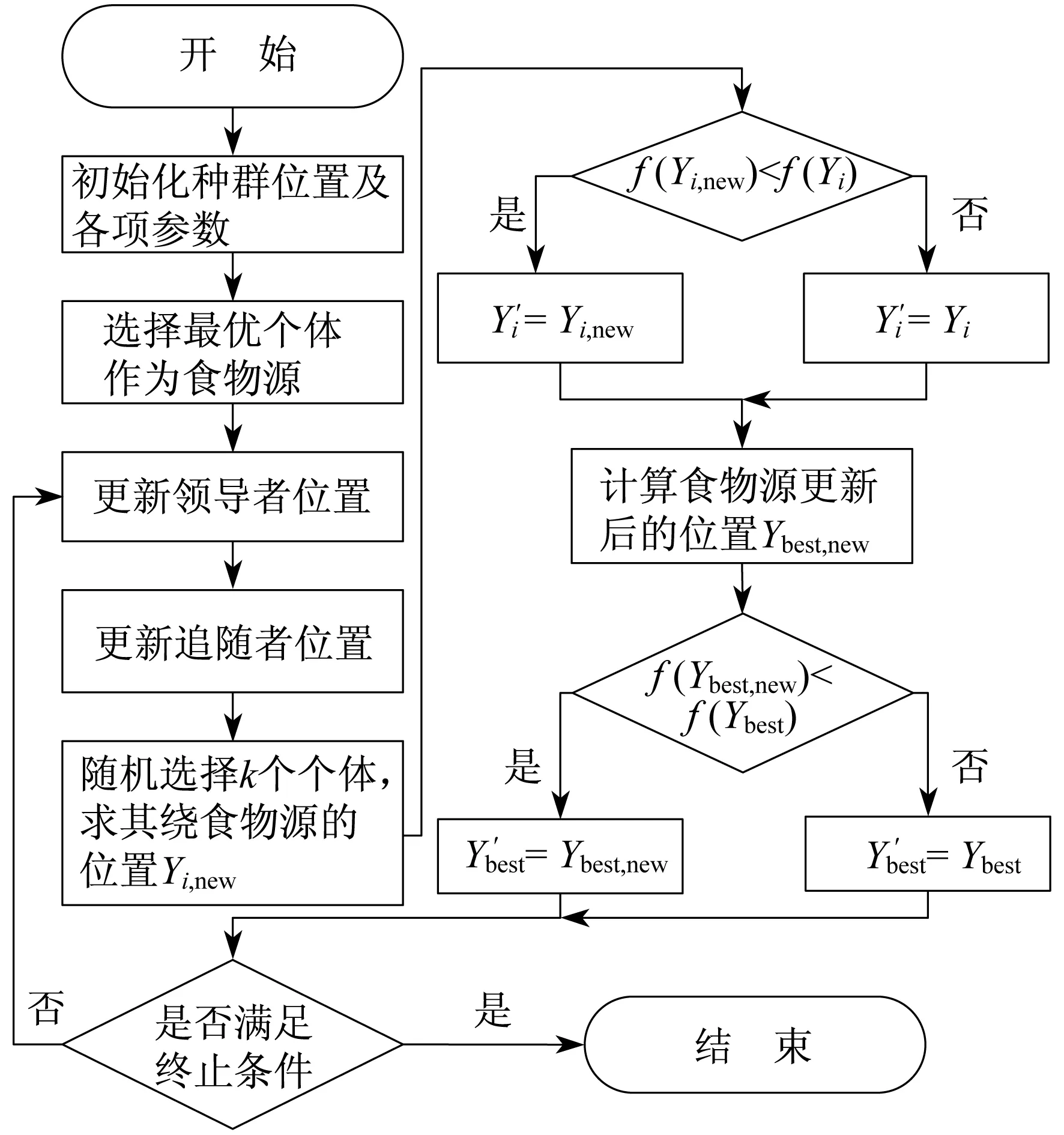
图1 ASSA的流程示意

2 实验分析

文献[4-5]中为了验证所提出的改进算法的有效性,将其与其他智能算法对基准函数进行了多次独立重复实验,并最终比较了各个算法的最佳值(Best)、平均值(Mean)、标准差(Standard Deviation,Std),以及算法的成功率(Success Rate,SR)。为了验证本文所提出的ASSA的有效性,对7个常用的测试函数进行最小值寻优仿真,并将结果与SSA、蚁狮算法(Ant Lion Optimization,ALO)[8-9]、灰狼优化算法(Gray Wolf Optimization,GWO)[10-11]、粒子群优化算法(Particle Swarm Optimization,PSO)进行比较,测试函数的详细信息如表1所示。其中,U表示单峰,M表示多峰,S表示可分,N表示不可分。

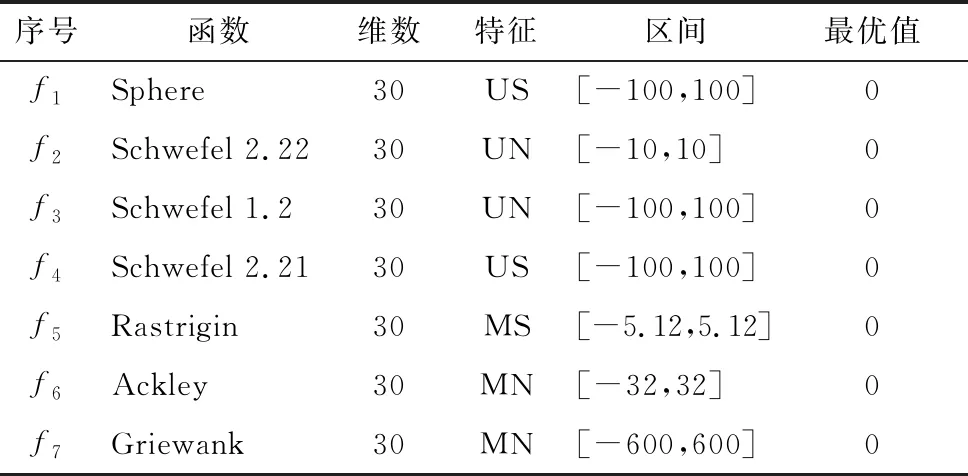
表1 测试函数信息

为了避免单次测试带来的偶然性影响,对每个函数进行30次独立实验,比较每种算法结果的最佳值、平均值、标准差和算法的成功率。判断每次试验是否成功的公式为

(8)

式中:FA——每次实际求解最佳值;

FT——测试函数理论最佳值。

算法参数设置如下:上述4种算法的种群数N=30;最大迭代次数tmax=200;PSO算法的惯性权重和学习因子分别为w=1,c1,PSO=c2,PSO=1.5[4];SSA和ASSA中领导者个数Nl和追随者个数Nf设成Nl=Nf[2,12-13],且Nl=Nf=N/2=15;ASSA中k=15%×N≈5。

表2为5种算法的实验结果。其中,最优值和平均值这两个指标能够很好地反映算法的收敛精度,而收敛精度的高低在很大程度上决定了算法的优劣。由表2可以看出,对于单峰函数f1～f4,ASSA的收敛精度非常高,达到了1.0×10-50以上,而SSA对这4种函数的寻优最优值均较大,其中对函数f3的寻优值甚至超过890,具有较大的误差。由此可见,ASSA能够改善SSA存在的收敛精度不高的问题。对于多峰函数f6,ASSA的收敛精度达到了1.0×10-16,远高于其他4种算法(GWO的收敛精度为1.0×10-5,PSO为2.7,SSA为5,ALO为8),满足了算法的精度要求。对于多峰函数f5和f7,ASSA收敛到了理论上的最优值零,这是其他算法所不能比拟的。

标准差和成功率能够反映算法的稳定性。ASSA的标准差远小于其他4种算法,采用ASSA优化的7个基准函数的标准差基本保持在1.0×10-30,SSA的标准差在1～200,GWO的标准差最好的也只有1.0×10-8。由此可以看出,ASSA对于不同函数的运算结果的稳定性比其他算法要好。对7个基准测试函数,在规定的200次迭代次数内,ASSA优化结果的成功率都是100%,而其他算法如GWO在对函数f3～f5时均难以达到100%,PSO和SSA的成功率甚至为零。

以上是基于30次独立运行的平均值、标准差的对比实验,无法反映每一次运行时各个算法之间的差异。文献[14]提出,应该对改进的算法进行统计性检验,以验证其是否具有明显优势。

因此,本文在5%显著性水平下进行了Wilcoxon秩和检验。在7个基准测试函数下,5种算法在Wilcoxon秩和检验中求得的p-value值如表3所示。将每个函数的最佳算法的值标记为N/A,以符号“+,=,-”分别表示ASSA的性能优于、等于和劣于相比较的算法。

文献[14]指出,p-value值小于0.05就可以被认为是拒绝秩和假设。由表3可以看出,与其他算法相比,ASSA的p-value值均小于0.05,可以认为在统计上ASSA比其他算法更具优越性,即ASSA具有更高的收敛精度。

文献[15]提出了一个有效并且可行的判别算法性能的指标,即为平均绝对误差(Mean Absolute Error,MAE)。其计算公式为

表2 各个算法的结果对比

表3 7个基准函数下5种算法的Wilcoxon秩和检验的pvalue值

(9)

式中:mi——算法多次独立测试后得到的最优结果的平均值;

Nb——测试函数的个数;

oi——测试函数的理论最优值。

本文同样用MAE来鉴别5种算法的优劣性,其结果如表4所示。

表4 5种算法的MAE排名

由表4可以看出,ASSA的MAE值最小,几乎为零,远远小于SSA算法的MAE值524,再一次验证了ASSA算法的优越性。

图2是5种算法对不同基准测试函数的平均收敛曲线。其中,ASSA在函数f5和函数f7的寻优过程中达到了最优值为零,故ASSA曲线的后面部分没有显示。

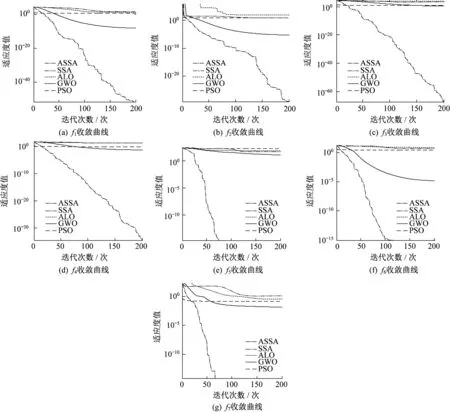
图2 不同基准测试函数下5种算法的平均收敛曲线

由图2可以看出,对于7个基准函数,ASSA的收敛速度很快,并且在200次的迭代中并没有出现陷入局部极值点的现象。其他4种算法的收敛速度远远不及ASSA,并且在迭代后期曲线平缓,下降速度慢,容易陷入局部极值点。对于函数f1,函数f3和函数f4,ASSA均以非常快的速度收敛,而SSA,GWO,ALO的收敛速度十分缓慢,PSO则容易陷入局部极值点;对于函数f2,PSO,SSA,ALO分别在迭代到18次、20次和100次左右便陷入局部极值;对于函数f5和f7,ASSA经不到100次迭代就达到了理论最优值,而其他3种算法依旧收敛速度缓慢,且最终精度也不高。

不论是针对单峰还是多峰函数,ASSA的收敛速度都很快,且收敛精度高。

3 结 语

本文在SSA的基础上,随机选取部分个体围绕全局最优个体进行位置更新,以探索最优个体附近的区域。通过7个基准测试函数对ASSA的性能进行检验,结果表明,ASSA的最优值、平均值、标准差等各项指标都十分优异,与SSA算法相比,其性能有了极大的提高。