基于STM32的步进电机动态加减速控制

何昌俊， 杨自栋， 闫珍奇， 曾 恒

(浙江农林大学 工程学院， 浙江 杭州 311300)

步进电机是一种可将电脉冲信号转变为角位移或线位移的开环控制元件。工作时，每输入一个脉冲，电机转轴即可转过一个相应的步进角，具有精度高、运行可靠及无累计误差等优点，因而被广泛应用于数字控制系统中。理论上，步进电机的工作状况只和脉冲数和脉冲频率相关。在实际中，随着脉冲频率的升高，步进电机转矩随之降低，当频率高到一定程度时，电机提供的转矩在一个脉冲周期里不能使电机转过一个步进角，此时电机将发生失步或堵转，所以步进电机存在一个最大工作转速。在步进电机速度发生突变时，若脉冲频率变化不合理，电机提供的转矩在一个脉冲周期里不能使电机转过一个步进角或超过一个步进角，电机将会发生失步、堵转或过冲，为此可以在步进电机变速时引入一个合理的加减速过程以解决这个问题。

常见的步进电机加减速控制方法主要有：直线型加减速曲线、指数型加减速曲线和S型加减速曲线。直线型加减速曲线在加速、匀速和减速过程中不能光滑过渡，主要适用于控制系统处理速度较慢且对升降速过程要求不高的场合；指数型加减速曲线的平滑性好，运动精度高，但在加减速的起点存在加减速突变；S型加减速曲线的加速度和速度曲线具有连续性特性，能够保证步进电机在运动过程中速度和加速度没有突变，减小冲击，从而提高步进电机的平稳性[1-2]。课题组根据ARM的STM32F103ZET6芯片，提出一种基于七段加减速S曲线的改进S曲线加减速算法，将其用于步进电机的动态调速中，提高步进电机运行时的稳定性和可靠性。

1 步进电机加减速S曲线

步进电机加减速S曲线，指的不是某一特定的算法，而是对加减速曲线呈S型算法的统称。常用的S型曲线主要有2种：一种是引入Sigmoid函数曲线作为加减速的速度曲线；另一种是在加减速阶段引入加加速度来控制加速度，以防止加速度突变出现柔性冲击而影响步进电机的平稳运行。

1.1 Sigmoid曲线

Sigmoid函数在生物学和信息工程学中是常见的函数。将Sigmoid函数图像向右平移a个单位，可作步进电机加速段的速度S曲线图，函数的表达式为式(1)，其导函数曲线可作步进电机S曲线的加速度曲线图，函数表达式为式(2)。图1所示的是a取5时Sigmoid曲线图和其导函数曲线图。

(1)

(2)

由图1(b)Sigmoid导函数曲线图可以看出，步进电机在加速阶段，加速度没有突变且没有拐点，整条加速度曲线光滑。说明Sigmoid函数做加减速S曲线可使电机避免加速过程出现刚性冲击和柔性冲击，有利于电机的加减速过程的平稳工作。但是在Sigmoid函数里含有ex项，当计算机处理这类函数时要花费远超加法和乘法运算的时间，故在STM32微控芯片上计算Sigmoid函数需要更长的时间。当芯片计算函数值的时间超过变频的时间时，会导致加速曲线出现不可预测的变化，从而导致电机运行的不平稳。

1.2 引入加加速度的S曲线

引入加加速度的加减速S曲线一般可分为包含加加速段、减加速段、匀速段、加减速段和减减速段的5段加减速控制曲线，以及包含加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段的7段加减速控曲线。常见的5段加减速曲线图如图2(a)所示；常见的7段加减速曲线图如图2(b)所示。

由图2(a)的加速度曲线图可以看出，在加、减速阶段，加速度图存在拐点，拐点的存在可能在运动中会引起柔性冲击。7段加减速曲线是基于5段加减速曲线的改进，由图2(b)和图2(a)加速度曲线图对比可知，在完成同样的加速过程的情况下，若加速时间相同，7段加速曲线中的最大加速度会更小，运行更稳定；若最大加速度相同，7段加速曲线会用更短的时间完成加速过程，即7段加速度曲线能更好地兼顾效率和平稳性。但7段加减速曲线，在加速度曲线上仍旧存在拐点，而且分段区间增多，控制算法变复杂，会影响实时控制系统的运算效率[3]。

2 构造7段加减速S曲线并优化

课题组针对7段加减速S曲线加速阶段中加速度存在拐点和加速阶段分段区间多，影响实时控制系统运算效率的问题，提出一种基于多项式拟合S加减速曲线的方法，在保留7段加减速曲线的优异加减速性能的同时，消除7段加减速曲线中加速度存在的拐点，使加速段或减速段成为单一的函数曲线。因此，课题组采用了大于三次多项式拟合加减速阶段的速度曲线。这样既可以保证速度曲线和加速度曲线连续可导，又能避免电机在运行过程中出现柔性冲击。

2.1 构造7段加减速S曲线

从图2(b)可知，曲线图上存在6个拐点，并以此为分界线。0～T1时间段内，速度由起始v0加速至拐点T1，加加速度a′为常数z，加速度a由0逐渐增加；T1～T2时间段，速度恒定增加，加速度为最大加速度amax；T2～T3时间段，速度减速增加，加加速度a′为常数-z，加速度a由amax逐渐减到0；T3～T4时间段,速度为恒速；T4～T5,T5～T6和T6～T7为减速段，与加速段类似，加速度变化为负值。

加速段S曲线方程如下：

1) 0～T1时间段内

加加速度为z(z>0)，加速度和速度方程分别为：

a=zt;

(3)

(4)

2)T1～T2时间段内

加速度为最大加速度，加速度和速度方程分别为：

a=amax;

(5)

(6)

3)T2～T3时间段内

加加速度为-z，加速度和速度方程分别为：

a=amax-z(t-T1);

(7)

(8)

4)T3～T4时间段内

速度为恒定值。

减速段T4～T5,T5～T6和T6～T7与加速段一致，可看作加速段的逆过程[4]。

2.2 优化7段加减速S曲线

对构造出的加速S曲线在隔开拐点处均匀取点，该取点方式可以更好地优化拐点处的函数曲线，采集的点集用数组的方式表示，记作pi(xi,yi)。对采集的数据点用多次多项式拟合，即对采集的数据点集做线性回归处理。

2.2.1构造优化模型

对拟合的近似曲线进行假设，其假设的线性回归模型的函数表达式为

(9)

式中：hθ(x)表示拟合曲线的函数值，θj表示函数多项式系数。

采用均方误差(MSE)作为线性回归模型的损失函数。损失函数的表达式为

(10)

式中：J(θ0，…，θn)表示均方误差，hθ(xi)表示在点xi处拟合曲线的函数值。

损失函数式(10)表示线性回归模型(拟合曲线上)的点与采集数据点偏差值的平方和，可用来描述线性回归模型与数据点集之间的差异。如果损失函数J(θ0，…，θn)=0，表示完全没有差异，则说明此线性回归模型完全描述数据之前的关系。如果需要找到最佳拟合的线性回归模型，就需要使对应的损失函数最小;求解最小损失函数的参数组，得到拟合曲线的函数表达式。

2.2.2求解最小损失函数

计算最小损失函数有2种实现方式：①梯度下降求损失函数最小值；②正规方程求解损失函数最小值。

2.2.2.1梯度下降原理

当选择梯度下降计算损失函数最小值时，开始随机选择一个参数的组合(θ0，θ1,…，θn)，计算损失函数;然后寻找下一个能让损失函数下降最多的参数组合，将该过程迭代，直到损失函数收敛到一个局部最小值。批量梯度下降的算法公式为

(11)

式中：“:=”是赋值符号，表示对左边变量进行赋值；β表示损失函数每次沿下降方向下降的程度。

2.2.2.2正规方程

求解损失函数最小值，即损失函数极值问题。对损失函数的参数(θ0，θ1,…，θn)求偏导数，令其为零，即可得到满足条件的参数组(θ0，θ1,…，θn):

(12)

采用单个方程逐一求解参数组中各参数的值，其求解的效率很低，因此可以采用矩阵的方式进行求解。用列向量θ表示损失函数的参数组(θ0，θ1,…，θn)，用m行n+1列的矩阵X表示m组n+1维的特征向量。用列向量Y表示(y1,y2,…,ym);列向量HθX表示(hθ(x1),hθ(x2),…,hθ(xm));J(θ)表示损失函数的值。拟合曲线的线性回归模型用矩阵可表示为

HθX=Xθ。

(13)

损失函数矩阵为

(14)

式(14)展开为

(15)

对各参数求偏导,得到

(16)

化简为

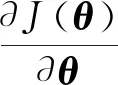
(17)

θ=(XTX)-1XTY。

(18)

式(18)为正规方程的表达式。

3 具体算法的实现

由于拟合曲线采用6次多项式，即拟合曲线只有7项特征，梯度下降和正规方程都能很快求解出损失函数最小值的参数，但相较而言梯度下降更擅长求解多特征的函数(特征值大于10 000)，正规方程更适合求特征值较少的函数。用MATLAB计算正规方程求解得到θ参数的组：

θ0=86.339 127；θ1=245.822 054；θ2=508.687 301；θ3=0.573 600；θ4=-3.256 022；θ5=0.197 272；θ6=-0.003 721。

拟合曲线的方程为

(19)

截取0～22.4 s内的频率导数拟合曲线，如图4所示。

4 动态调速

在实际运行过程中，频率的变化是离散的，需要对曲线离散取值。课题组采用等时间间隔数值的阶梯逼近升速S曲线取值，等脉冲数为阶梯实际维持长度的方案，示意图如图5所示[6-9]。

对于阶梯的维持时间的长度有等时长和等脉冲数2种方案。

1) 等时长方案。每个阶梯维持相同的时间，它能很好地反映S曲线的特性，但是第1个阶梯的脉冲数和最后1个阶梯的脉冲数相差很大。步进电机在调速时，步进电机的转子转过第1个步进角停下的位置时，转子会出现一定程度的震荡。为解决该震荡，需要增加几个同频脉冲使转子运行平稳，但同频脉冲过多并不会继续提高其平稳性。

2) 等脉冲数方案。每个阶梯维持相同的脉冲数。在选取了合适的同频脉冲数后，能对S曲线的性能进一步优化，提高运行的效率。

选取同频等脉冲数作为阶梯维持时间，能在保持近乎相同的性能下，提高运行效率。经试验测得，5作为同频脉冲数是一个较合适的值[10]。

取图5中S曲线与阶梯的接触点为离散的取值点，记为(tk,fk)。k表示S曲线上取的第k个点，fk表示第k个点运行的频率，tk表示第k个点时间的数值。图5中Δt表示等时间间隔数值,Δtk表示以(tk,fk)为起点的实际阶梯时间维持长度，即图中第k个灰柱条的宽度。

第k个阶梯实际的维持时间为

Δtk=w·tplusek。

(20)

在tk点的实际运行时间为

(21)

式中：tplusek表示第k个点单个脉冲持续的时间；tplusem表示第m个点单个脉冲持续的时间;w表示同一频率脉冲的个数。

在动态调速过程中，脉冲频率(速度)增加的数值可以是0～90 000 Hz之间的任意值，所以不可能为每一个调速建立一个S曲线。为了实现范围调速，可以先建立一个通用的S曲线模型，然后对其进行拉伸、压缩以对应不同的调速。拉伸和压缩后的曲线仍会保留大部分原曲线特性。

通过给S曲线函数乘以一个系数ε得到需要的增速，即在纵轴上对实际S曲线进行压缩[11]。针对不同的增速，可选取相对应的等时间间隔数值Δt和同频脉冲数，保证动态调速的效率和稳定性。经多次试验表明，此方法有良好的动态调速性能。

经过试验发现，可以先获得某一同频脉冲数下步进电机不发生堵转的初速度、增速和等时间间隔数值Δt的临界关系表。然后取临界等时间间隔数值Δt′的1/4为稳定等时间间隔数值Δt″，可得到初速度、增速和等时间间隔数值Δt稳定关系表。

将初速度、增速和等时间间隔数值Δt稳定关系图表作为动态选择等时间间隔数值Δt的依据，协同优化后的S曲线算法写入内存，即可作为动态调速控制的核心，实现对步进电机进行平稳的动态调速。

5 结语

课题组通过优化七段加减速S曲线，在保留其优良特性的同时，消除加速度曲线存在的拐点，并将加或减速过程中的3段函数用1段函数替代，降低算法的复杂性，同时精简了代码。基于优化后的S曲线，采用等时间间隔数值的阶梯逼近升速S曲线取值，等脉冲数为阶梯实际维持长度的方案用于实际控制步进电机。经试验得到初速度、增速和等时间间隔数值Δt使电机平稳运行的关系。试验表明，采用本研究所述方法，步进电机在指定的范围内能进行平稳的动态调速。