含运动分岔闭链的多运动模式并联机构

王 艳， 许 勇， 董 飞， 张强强， 赵传森

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

运动分岔机构是指通过奇异位形前后，自由度特性(自由度数目或类型)及相应位形发生改变的机构[1]。运动分岔机构是新兴的可重构机构，可作为变自由度可伸展机构、多轴联动多面加工装备和多步态灵活移动装置的运动执行机构，无疑具有很高的研究价值和广阔应用前景[ 2-3]。课题组将机构的特定自由度及其相应位形称为机构的运动模式。

奇异位形是运动分岔机构不同运动模式间的瞬时转换位形[4]。通过在奇异位形中引入新的驱动副，运动分岔机构可离开瞬时奇异位形，切换为连续运动模式[5]。对运动分岔机构来说，奇异位形往往是自由度切换位形，而非需要避免的失控位置[6]。

课题组将运动分岔特性引入到并联机构中，提出了新构型的运动分岔并联机构。课题组认为，分岔机构在通过瞬时奇异位形前后自由度发生改变的根源，在于分岔机构支链中约束特性(约束螺旋数量或轴线方向)的改变，因而机构支链中必定存在着多个线性相关的约束螺旋，这通常由通过切换驱动副从而实现过约束的分岔闭链来实现[7]。所以可认为分岔机构的变自由度特性来自于分岔闭链。

目前研究者们已经提出了一些运动分岔机构：LI等提出了具有不同schoenflies运动分岔特性的并联机构[8];Galletti等提出了许多具有运动分岔特性的机构[9];ZENG等提出了一款4自由度混联分岔机构[10]；LEE等提出一种广义运动分岔机构是运动限定6R机构[11]58；叶伟等利用单环闭链的约束奇异特性提出一系列可重构并联机构[12-14]。

课题组提出了一种URRC(万向节-转动副-转动副-圆柱副)构型的运动分岔闭链，具有单自由度整体空间连续转动或者单自由度平面连续运动2种运动模式。以此运动分岔闭链为核心单元，构建了具有5自由度和6自由度运动模式的混联支链，及具有3转3移、3转2移、3转1移和2转1移共4种运动模式的并联机构。基于螺旋理论[15]对分岔闭链、混联支链及并联机构的自由度进行了分析，验证了多运动模式分岔闭链、支链和并联机构构型设计的合理性。

1 运动分岔闭链自由度分析

1.1 运动分岔闭链奇异位形下瞬时自由度分析

课题组提出的具有运动分岔特性的闭链如图1所示，闭链的构型为URRC(万向节-转动副-转动副-圆柱副)。LEE[11]60所提出的运动限定6R机构由2个转动副和2个万向节连接的4杆组成，该机构可以执行平面4杆运动和单轴转动运动。课题组提出的闭链用圆柱副代替了LEE[11]61所述的一个万向节，可以执行平面曲柄滑块连续运动和整体空间连续转动。

机架与构件AS在A点通过圆柱副相连，构件AB与构件AS在A点以转动副连接，构件AB与构件BG在B点以转动副连接，机架与构件BG在G点通过万向节相连，其中构件BG长度为a，AG长度为b，其中A,B,G为运动副形心。

选取图1中构件AS为输出构件，该输出构件右端通过支链1(包含转动螺旋SA1和移动螺旋SA2)，左端通过支链2(包含转动螺旋SA3,SB,SG1和SG2)与机架连接。则支链1和支链2的运动螺旋分别为:

(1)

(2)

对式(1)和式(2)取反螺旋可得支链1和2的约束螺旋为：

(3)

(4)

由(3)和式(4)可得2条支链的在奇异位形下的公共约束为：

(5)

因此，奇异位形下的公共约束数λ=2，机构的阶数d=6-λ=4。奇异位形不存在并联冗余约束，由修正的G-K公式可得在奇异位形下闭链瞬时自由度为：

(6)

式中：M表示机构的自由度；n表示包含机架的构件数；g表示运动副的数；fi为第i个运动副的自由度数;v代表并联冗余约束数。

SB·SG1=sinα·sinβ=0。

(7)

由式(7)看出，α=0且β=0时即为奇异位形；α=0或β=0时为一般位形，且α=0和β=0不能同时存在。

1.2 运动分岔闭链模式Ⅰ自由度分析

(8)

(9)

(10)

由式(9)和(10)可得该闭链公共约束为0，机构的阶d=6。2条支链共有6个约束螺旋线性相关其秩为5，存在并联冗余约束v=1。在此位形下闭链的自由度数为:

M=6(4-4-1)+6+1=1。

(11)

对式(14)和(15)的约束螺旋系取反螺旋可得构件AS的运动螺旋为

(12)

由式(12)可见,当β=0，α为任意角时，构件AS的自由度为1，运动为绕x轴的连续运动。如图2(b)所示，此时闭链整体被刚化称为单自由度整体空间转动连续运动模式。

1.3 运动分岔闭链模式Ⅱ自由度分析

(13)

式中：(xA,yA,zA)表示A点坐标。

(14)

(15)

由式(14)和(15)可得该闭链公共约束为0，机构的阶d=6。2条支链共有6个约束螺旋线性相关其秩为5，存在并联冗余约束v=1。在此位形下闭链的自由度数为

M=6(4-4-1)+6+1=1。

(16)

对式(9)和(10)的约束螺旋系取反螺旋可得构件AS的运动螺旋为:

(17)

由式(17)可见，当α=0，β为任意角时，构件a的自由度为1，运动为沿x轴的平移运动。如图3(b)所示，此时整个机构称为单自由度平面运动连续运动模式。

2 运动分岔混联支链自由度分析

2.1 混联支链5自由度模式

(18)

对式(18)运动螺旋求其反螺旋，可得混联支链的约束螺旋为：

(19)

式中：(xD,yD,zD)表示D点坐标;(xE,yE,zE)表示E点坐标;(xF,yF,zF)表示F点坐标。

如用该混联支链组装得到并联机构，由式(19)表明，模式Ⅰ时混联支链对动平台施加一个约束力线矢，该力线矢与固定坐标系x方向相同且通过球面副所在的F点，此时混联支链为5自由度模式。

2.2 混联支链6自由度模式

(20)

由式(20)可见，模式Ⅱ时混联支链的运动螺旋秩为6，则混联支链无约束作用于动平台，混联支链模式为6自由度模式。

3 运动分岔并联机构运动模式自由度分析

如图6所示，利用3条对称布置的URRC-RRS混联支链组装为运动分岔并联机构。混联支链的运动分岔闭链与定平台相连，混联支链的球面副与动平台相连。建立定坐标系o0-x0y0z0于定平台的几何中心，x0方向与混联支链1的机架方向平行，y0垂直于定平台，z0由右手定则确定。建立动坐标系o1-x1y1z1在动平台的运动中心，其方向与定坐标系一致。

3.1 3转3移运动模式

若并联机构的3条混联支链都工作在6自由度模式，此时将无约束作用于动平台。该运动模式下并联机构的自由度为6，可实现图7所示的3转3移运动模式。

3.2 3转2移运动模式

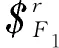
(21)

式中：P1,Q1和R1为常数。

由式(21)可知，该约束力线矢作用于混联支链1球面副F1上且与动平台x1正方向平行，它约束了运动平台沿x1方向的移动。在该模式下可实现图8(b)3转2移运动模式。

3.3 3转1移运动模式

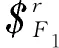
(22)

式中：Pi,Qi和Ri(i=1,2)为常数。

3.4 2转1移运动模式

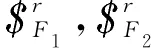
(23)

式中：Pi,Qi和Ri(i=1,2,3)为常数。

由式(23)和图10(b)可知，3个约束力线矢共面、不平行也不汇交一点，它们约束了动平台沿x1和z1的移动及绕y1的转动。可见在该模式下可实现2转1移运动模式。

4 支链输入副选取合理性分析

根据输入选取原理[17]，锁死所有输入运动副后，若动平台约束螺旋的秩为6，则动平台将失去全部6个自由度，选取合理。锁死奇异位形下每一支链的2个输入运动副，每一支链的机构被刚化，如将混联支链的定坐标系o-xyz平移至转动副D的形心，此时混联支链的运动螺旋为:

(24)

对式(24)取反螺旋得混联支链的约束螺旋为:

(25)

式中：Δy=yF-yE;Δz=zF-zE。

由式(25)可见，刚化输入副后，动平台将受到每条混联支链2个约束力线矢的作用。一个约束力线矢与定坐标系x轴平行；另一约束力矢平行于构件EF。

在定坐标系下，并联机构的约束螺旋为:

(26)

式中：d为定平台中心o0到等边三角形各边的距离。

由式(26)可见，在定坐标系下，动平台约束螺旋的秩为6。如输入副被刚化，并联机构的动平台将失去6个自由度，所以输入方案选取是合理的。

5 结论

1) 课题组提出一种构型为URRC运动分岔闭链，闭链具有2自由度奇异位形下的瞬时运动，一般位形下有单自由度整体空间连续转动或者单自由度平面连续运动2种互斥运动模式。

2) 将运动分岔闭链与5自由度RRS开链串联得到一种混联支链。该混联支链具备2种独立运动模式，输入副不同可使得混联支链在5自由度模式和6自由度模式切换。

3) 利用3条对称布置的URRC-RRS混联支链得到运动分岔并联机构。混联支链模式选取不同，运动分岔并联机构具有3转3移、3转2移、3转1移和2转1移4种不同运动模式。