求解分数阶常微分方程的一个高阶数值逼近格式*

曹文平，肖承家，王自强

(贵州民族大学 数据科学与信息工程学院，贵州 贵阳 550025)

0 引言

20世纪70年代末， Mandelbrot[1]提出了分形学说，并且将Riemann-Liouville分数阶微积分用以分析和研究分形媒介中的布朗运动以后，分数阶算子尤其是分数阶微积分和分数阶微分方程理论及其应用研究在国际上才得到广泛关注和迅速发展。

与整数阶微分方程不同，分数阶微分方程的理论研究在文献中很少看到。Diethelm等人考虑了分数阶常微分方程(FODEs)初值问题解的适定性[2]， Kilbas等人利用广义的Mittag-Leffler函数研究了Volterra integro-differential方程的解的表达式[3]，Diethelm[4]给出了FODEs理论方面的最新发展。

给定一个一般的右端项f，确定分数阶微分方程的解析解是相当困难的。因此，我们必须寻找有效求解FODEs的数值方法。

我们考虑分数阶常微分方程如下：

(1)

且满足如下的初值条件：

y(0)=y0

(2)

(3)

其中表达式Γ(·)表示Euler Gamma函数。

对于方程(1)的数值方法，许多研究者们已经做了大量的工作[6]。文献[7，8]将(1)式转化为Volterra型积分方程，则可利用积分方程的一些技巧建立了高阶数值格式。本文中，我们利用二次拉格朗日插值来逼近分数阶导数，得到了一个高阶数值逼近格式。

本文第一部分， 详细地构造了一个高阶数值逼近格式; 第二部分，列出了所构造数值格式的局部截断误差估计; 第三部分，用一系列算例来验证理论预测的正确性。

1 高阶数值格式

为了构造高阶数值逼近格式，我们将区间[0，T]分成2N个等分的子区间，设：

h=T/(2N)，记xj=jh，j=0，1，…，2N

在xj处的数值解记为yi，且

下面，我们开始构造高阶数值逼近格式。

(4)

对于子区间[x2k，x2k+2]，k=0，1，…，m-1，y(x)的逼近形式如下：

(5)

其中φi，k(x)，i=0，1，2；k=0，1，…，m-1，是定义在点x2k，x2k+1，x2k+2上的二次拉格朗日基函数：

(6)

对于子区间[x2m，x2m+1]，y(x)的逼近形式为：

(7)

(8)

于是，

[I[x2m，x2m+1]y(s)]′ds

(9)

其中：

i=0，1，2；k=0，1，…m-1

(10)

i=0，1，2

可知，(10)式是可以精确计算出来的。y2m+1/2通过下面的插值来获得：

(11)

因此，第2m+1步的数值格式如下：

(12)

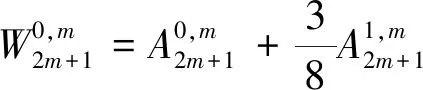
(13)

对于[x2k，x2k+2]，k=0，1，…，m，y(x)的逼近式见(5)式，且φi，k(x)，i=0，1，2；k=0，1，…，m，见(6)式。于是，

[I[x2k，x2k+2]y(s)]′ds

其中：

因此我们得出2m+2步的数值格式:

(14)

综上所述，结合(12)式和(14)式，我们得到数值格式如下：

(15)

2 局部截断误差估计

数值格式(15)的局部截断误差估计如下。

定理1.假定y(x)∈C4[0，T].设：

(16)

|rk(h)|≤Ch3-α，k=1，2，…，2N

(17)

其中C是一个依赖于y但与h无关的常数。

3 数值算例

我们要进行一系列数值试验，来测试格式的有效性。准确地说，我们的主要目的是验证数值解关于时间步长h的收敛行为。

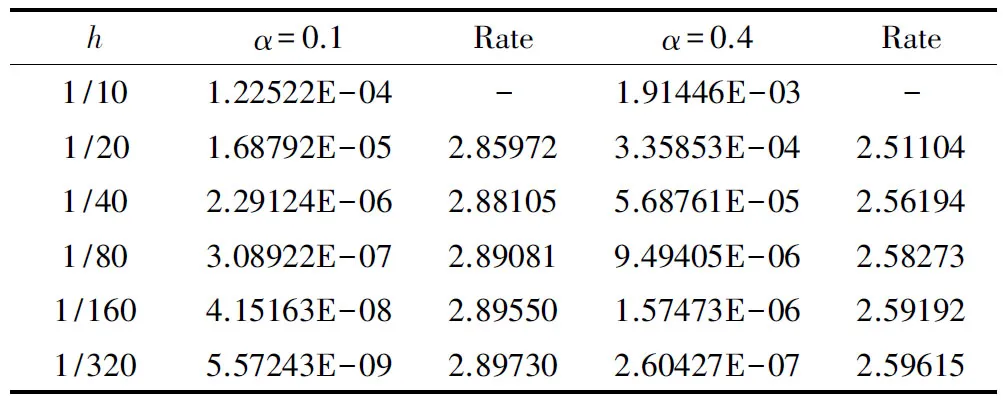
表1 算例1中α=0.1，0.4，最大误差随时间步长h的变化与收敛阶Tab.1 Maximum errors and decay rate as functions of h with α=0.1，0.4，for Example 1

表2 算例1中α=0.7，0.99，最大误差随时间步长h的变化与收敛阶Tab.2 Maximum errors and decay rate as functions of h withα=0.7，0.99，for Example 1

例2，考虑初值问题(1)-(2):

其中λ是一个常数。注意到此时f是y的线性函数，相应的精确解为y(x)=x3+α。

首先，取λ=1，表3、表4重复例1的计算过程，我们得到取α从0.1到0.99时，最大误差接近于3-α，这支持了理论分析的结果。

表4 算例2中α=0.7，0.99，最大误差随时间步长h的变化与收敛阶Tab.4 Maximum errors and decay rate as functions of h withα=0.7，0.99 for Example 2