基于自动导引车单向导引路径网络的智能车间设备布局规划

王 闯,常丰田,高佳佳

(1.西安邮电大学 物联网与两化融合研究院，陕西 西安 710061; 2.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安 710054; 3.西安交通大学 机械工程学院，陕西 西安 710049)

0 引言

生产车间设备布局设计是将加工设备、物料输送设备、工作单元和通道走廊等布局物体合理地放置在一个有限的生产空间内的过程[1]。基于自动导引车(Automated Guided Vehicle, AGV)的生产设备布局是整个智能车间布局规划的核心问题之一。传统车间生产设备布局设计规划方法是基于生产车间物流量最小目标建立设备布局模型，在考虑约束条件下，通过各种优化算法得到最终布局方案[2]。钱骏等[3]应用单元生产分析的方法，以某机加工车间转子的整个加工流程为研究对象，通过对该转子零件的加工流程分析，设备布局分析以及在制品分析，提出转子加工的改善方案。周娜等[4]在设备混合布局问题研究中，提出了“田”分形理论，并通过总运输成本和布局占用面积最小化为优化目标，实现对车间设备的布局设计。丁祥海等[5]研究了U型生产单元重构设施布局问题，构建了具有预算约束的单元物料搬运成本、单元重构成本、生产时间损失成本的重构设施布局模型。熊佳玮等[6]利用MATLAB和Python语言对仿真生产实验平台设备布局系统进行设计与开发，采用GA-Lyaout算法进行优化，并且对Python、Flexsim等软件开放接口，降低了重构车间布局的设计难度，增强了可操作性及便利性。陈春鹏等[7]根据机床数量以及型号进行功能区划分和功能区布局，以物流时间最短为目标进行总体布局。何坤等[8]以某航天所某零件的加工车间为例，使用模拟退火遗传算法对该车间进行布局评价。杨挺等[9]结合多行多区域车间的特点，通过定义包含设备位置点、通道位置点和转向位置点的网络节点以及邻接矩阵，构建设备布局网络模型，给出了设备之间最短物流路径的求取方法与步骤。在生产设备布局设计规划问题中，工程界主要针对具体生产场景和需求进行研究[10-12]，而学术界开始将各种优化算法应用到最优布局的求解中[13-16]。郑永前等[17]设计了基于结构化编码的动态多种群粒子群优化算法，对单元构建与单元布局同时进行描述求解。Palomo-Romero等[18]在不等面积设施布局问题上引进了岛模型遗传算法。左兴权等[19]双行设备布局问题，提出一种结合多目标免疫算法和线性规划的双行设备布局方法，同时实现优化物流成本和布局面积两个目标。

然而，传统的设备布局设计规划方法采用两个设备之间的直线距离或者曼哈顿距离作为优化变量，而没有考虑工件搬运设备在实际物料搬运过程中行驶的路线[20]。这必然导致最终选择的生产设备布局方案，在物流路径和物流效率上无法做到最优。由于传统车间的工件搬运设备主要通过人工控制或操作，对物流路径优化和物流效率的要求相对较低。但是智能车间中往往采用AGV作为搬运工具，显然，基于直线距离或者曼哈顿距离的传统设备布局方案就具有一定局限性[21-22]。从目前的文献分析来看，基于AGV的智能车间生产设备布局设计规划问题还没有得到深入研究。

本文以缸盖柔性生产设备布局为例，针对智能车间设备布局设计规划问题，采用与AGV路径优化相结合的方式，提出一种双层嵌套遗传算法。外层遗传算法以物流成本最小为目标优化车间设备布局，其物流成本的计算需依赖内层遗传算法优化后的路径得出。将混沌思想引入到遗传算法中(Chaos Genetic Algorithm，CGA)，以提高优化效率，有效地避免简单遗传算法早熟与局部收敛问题。

1 问题描述

1.1 传统车间设备布局建模

车间设备布局是指不考虑生产车间设加工设备的具体形状，将其简化成规则的矩形，用矩形包络加工设备的最大外形尺寸，将包络矩形作为设备的简化矩形，在给定的车间范围内，确定每个布局对象在空间的具体位置，传统设备布局建立问题模型如图1所示。图中：L表示车间长度，H表示车间宽度，(xi,yi)表示设备i的中心坐标，(dij)m表示设备i和设备j中心坐标之间的曼哈顿距离，(dij)o表示设备i和设备j中心坐标之间的欧式距离。

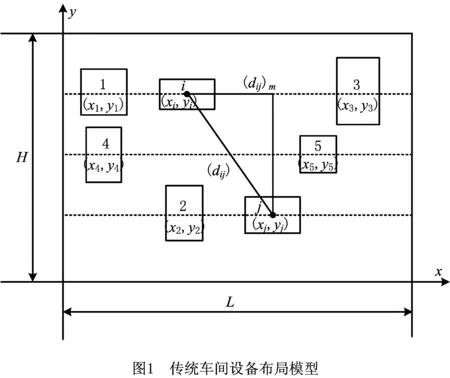
常用的布局优化目标函数如下：

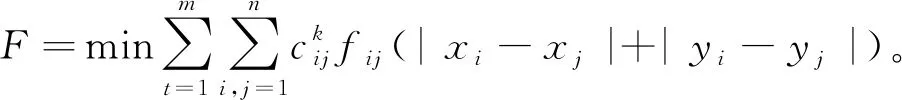
(1)

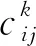
1.2 传统设备布局规划方法优缺点

传统设备布局通过对物料搬运过程中产生的物流成本建模，并进行优化搜索得到最佳的布局方案。在直线单行布局模式中，搬运工具在搬运过程中行走的距离，即为两个设备之间的直线距离，通过式(1)来表示物流成本是合理可行的。研究表明，在其他布局模式中，如果搬运工具在运行过程中没有运行轨道及运行方向的限制，通过两个设备间的曼哈顿距离来表示搬运工具的运行路线可以有效地避免搬运工具之间的来回交叉运行，是最合理的。然而，在以AGV作为搬运工具的智能生产车间中，单向导引路径网络具有运行效率高等其他导引路径网络无法比拟的优势，因而成为AGV系统的最佳选择。此时，通过欧式距离和曼哈顿距离来计算物流成本显然是不合理的。

1.3 智能车间中设备配置形式及特点

智能车间中机床设备的配置有互替式、互补式以及混合式等多种形式，以满足生产过程的柔性和高效率要求[23]。在互替式机床配置中，各机床设备是一种并联关系，其功能可以互相代替，工件可随机输送到任何一台恰好空闲的机床上加工，在这种配置形式中，若某台机床发生了故障，系统仍能维持正常的工作，具有较大的工艺柔性和较宽的工艺范围，但是生产车间的设备购置成本相对比较高，对车间的布局面积也会有所增加。在互补式机床配置中，各机床设备功能是互相补充的，各自完成特定的加工任务，工件在一定程度上必须按顺序经过各台加工机床。这种机床配置形式的特点是具有较高的生产率，能充分发挥机床的性能，但由于串联配置，降低了系统的可靠性。基于前面两种配置形式的特点和问题，在实际智能车间的加工设备配置中较多采用混合式配置，即有些机床按互替形式布置，有些则按互补形式布置，发挥各自的优点。

2 基于AGV单向导引路径的设备布局建模

2.1 约束条件及前提假设

为了使模型更具有普适性，本文针对实际生产中较常采用的直线双行布局进行数学建模[24]，如图2所示。并对实际生产场景做以下简化处理：①每台设备尺寸相等；②设备的上下料点在同一位置。同时，约定以下行和列设备布局规则：①行方向的约束条件：一台设备只能布置在某一行中，且只能出现一次；同一行内，相邻设备之间为最小间距约束，即保证两相邻设备之间不能出现干涉或重叠；设备与车间墙壁之间有最小间距约束。②列方向的约束条件：同一行设备的纵坐标相同；相邻行之间为最小间距约束，保证设备在y方向上不出现干涉或重叠。

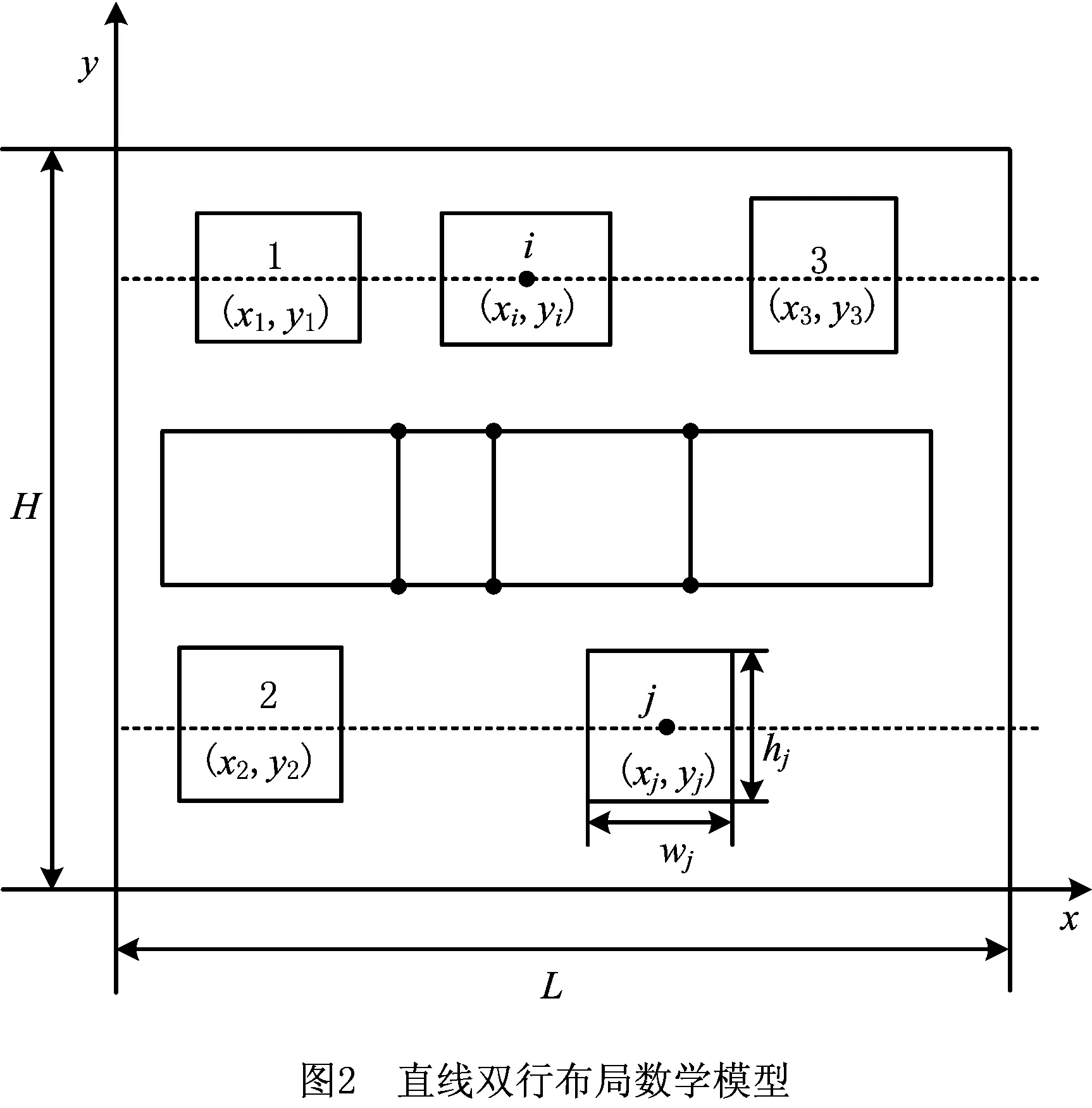
2.2 数学描述

设从设备mi到设备mj的缸盖搬运频率为fij，则

(2)

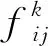
以物流成本最小为目标函数，其优化目标函数为：

(3)

无向路径的生成规则如下：

(1)对每排机床，连接上下料点产生两条横向路径；

(2)同一排机床中每两台相邻机床间产生一条纵向路径连接两条横向路径；

(3)当纵向路径间距离小于给定值(由计算得出)时路径合并。

对生成的无向导引路径网络，以搬运矩最小为目标确定路径方向，目标函数为：

(4)

3 基于优化路径的生产设备布局算法解算

设备布局问题属于NP-Hard问题。事实证明，通过传统最优化方法解决此类问题需要较长的时间。而运用智能搜索算法往往需要对个体(即每个设备布局方案)评价，而对设备布局方案质量的评价，需要求解此布局方案下较优的单向导引路径网络，这也属于NP-Hard问题。混沌优化方法将问题变量从解空间转换到混沌空间，利用混沌变量随机性，遍历性和规律性的特点进行搜索，从而找到所需解决问题的最优解。本文借助混沌优化方法的这一特点，将遗传算法与混沌映射算子相结合，提出一种混沌遗传算法来实现对基于优化路径的生产设备布局算法解算。

3.1 求解多行设备布局问题混沌遗传算法

(1)设备布局染色体编码

设备布局染色体采用实数编码的方式来进行编码，将布局方案中各台加工中心的中心位置的横纵坐标组成的字符串作为染色体，以10台加工中心为例，该字符串可以表示为[x1,1x1,2x2,1x2,2…xi,1xi,2…x10,1x10,2]。其中：[x1,1x1,2]表示设备1中心位置的坐标，[xi,1xi,2]表示设备i中心位置的横纵坐标。将混沌思想引入到待优化的设备坐标变量中，通过映射的方法得到初始种群。[ai,bi]为设备布局染色体中第i个变量的取值范围，当i为奇数时，[ai,bi]为设备横标在车间长度方向的取值范围；当i为偶数时，[ai,bi]为宽度方向的取值范围。种群规模设定为100。

通过Logistic映射，可以得到混沌变量的初始种群为：

(5)

式中:i表示混沌变量的序号，i=1，2，…，20；u表示种群序号，u=0,1,…,99；βi表示混沌变量，0≤βi≤1；μi表示吸引因子。

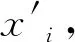
(6)

式中ci和di均为常数。

通过以上计算得到优化变量的染色体及初始种群，即设备中心位置坐标的染色体及初始种群，如下所示：

(7)

(2)随机扰动

令

(8)

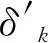
(3)适应度计算

优化函数的适应度为：

(9)

式中：K为常数；F表示生产设备布局目标函数；P为惩罚项，当染色体满足所有约束条件时，P=0，当染色体不满足所有约束条件时，P为一个值比较大的正整数。

(4)混沌遗传操作

1)通过适应度函数，计算每一代个体的适应度值。对计算得到的适应度值按从大到小的顺序进行排列。由于当某一代群体中适应度值差异较小时，会使收敛速度非常慢。经过调整后，种群中染色体的适应度值具有明显差异，对加快收敛速度产生有利的影响。

2)对于排序后的种群，取其适应度值最大的10%直接作为下一代种群中的染色体，剩余90%的染色体进行遗传操作以后进入下一代。

3)对得到的新的种群，计算其调整后的适应度值，并按适应度值从高到低的顺序进行排列。将该群体中最大适应度值与平均适应度值进行比较，如果小于设定的差值，则停止寻找最优解，否则进行下一步操作。

(10)

4)保留种群中适应度值较高的10%的染色体，对于适应度值较低的90%的染色体，再加一随机扰动，将经过随机扰动后的混沌向量计算调整后的适应度值，如果前后两次迭代得到的适应度的平均值之差小于某一足够小的正数ε2，则停止迭代，否则，继续迭代。随着迭代的进行，染色体逐渐趋向最优解。

(11)

5)对当前种群计算适应度值，若该种群满足式10，则寻优过程结束，并将最优解输出，若不满足，则转第2)步，进行下一轮混沌遗传操作。

4 缸盖智能生产车间设备布局规划实现

本文以某缸盖智能生产车间的设备布局规划问题，对以上优化模型的实现过程进行分析验证。目前该车间主要生产十几余种船用发动机缸盖，其主要加工设备为10台加工中心：THM6380。根据每周的平均缸盖产量，通过式2得到设备之间的缸盖搬运频率矩阵如表1所示。

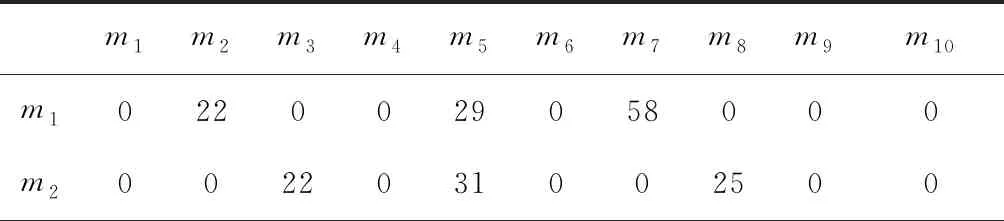
表1 缸盖搬运频率

续表1

注：表中m指车间内主要加工设备。

4.1 缸盖智能生产车间设备布局嵌套遗传算法求解与实现

按照直线双行布局模式，将设备中心位置横坐标按照从小到大的顺序进行排列，得到z1,z2,z3,…,z10，设路径网络各个节点坐标为(pi,qi)，则(pi,qi)的生成方法为：

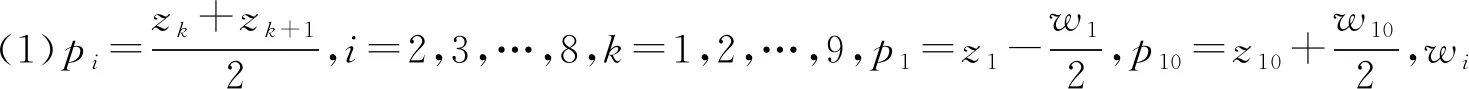
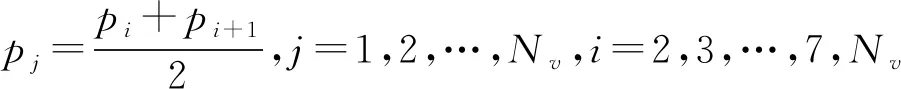
4.2 基于MATLAB的算法实现

基于优化路径的设备布局程序在Microsoft Windows 7系统环境下通过MATLAB进行编写，将本文所提算法与传统设备布局中常使用的遗传—模拟退火算法(GA-SA)和简单遗传算法(SGA)收敛曲线进行比较，比较结果如图3所示。

经过20次程序运行，将其平均物流成本和平均计算时间与遗传—模拟退火算法和简单遗传算法进行比较，如表2所示。

表2 不同布局优化算法结果对比

由图3的实现结果，可以看出本文所设计的混沌遗传算法在收敛速度和适应度值方面均优于遗传—模拟退火算法和简单遗传算法，从表2也可以看出，本文所应用的混沌遗传算法可以搜索到的最优解在物流成本方面优于其他两种方法。

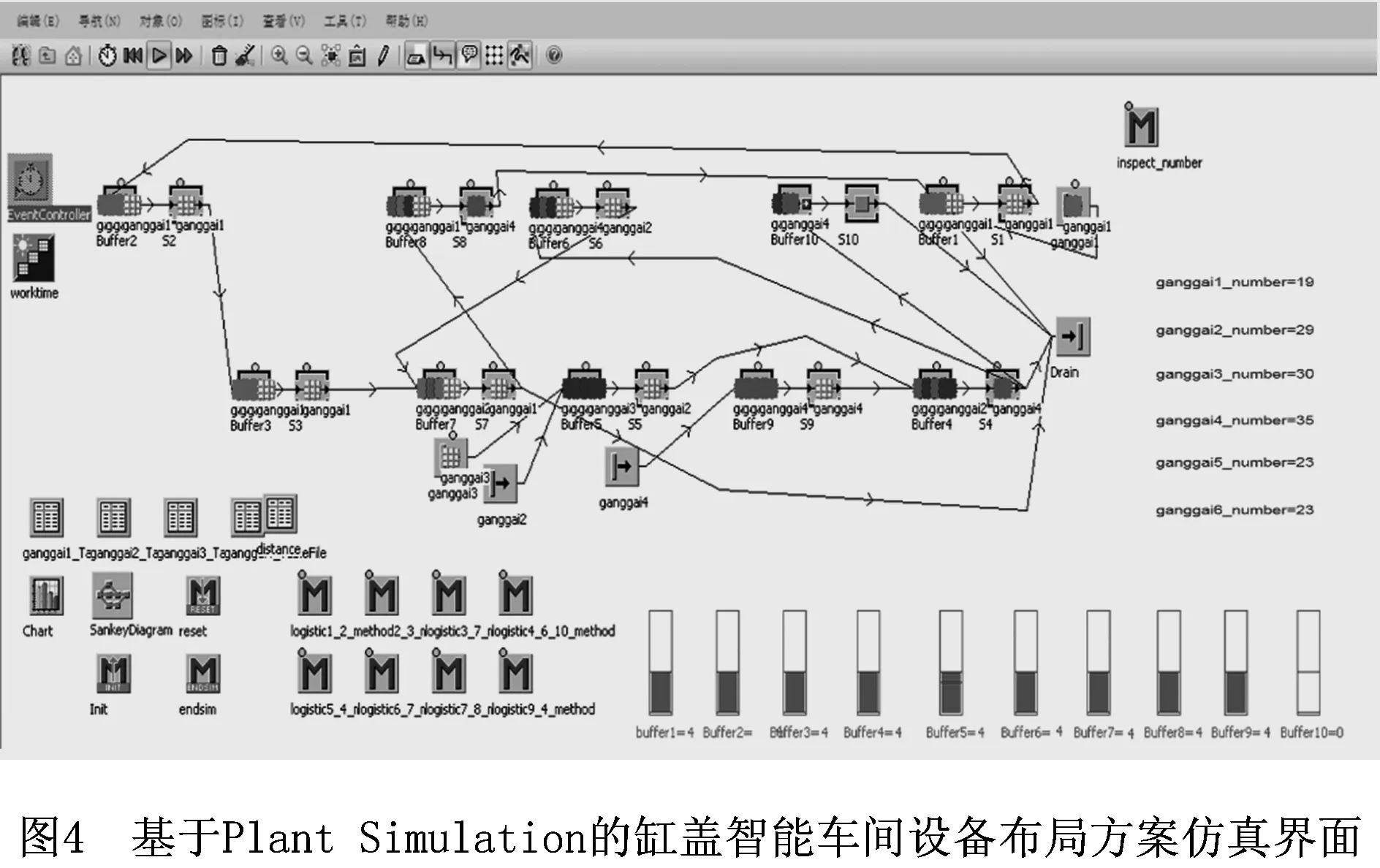
4.3 基于Plant Simulation的仿真实验

由于缸盖生产过程情况比较复杂，为了进一步对本文所提方法及模型的有效性进行验证，此处采用Plant Simulation构造缸盖智能车间生产过程并进行仿真实验，其仿真界面如图4所示。根据各台设备的坐标值确定每台设备的位置，其中3种布局优化算法得到的布局方案仿真运行一周以后，对应的6种缸盖的一周产量结果如表3所示。从仿真结果看，本文基于AGV单向导引路径网络的智能车间生产设备布局规划CGA算法可以进一步提高制造车间的生产能力。

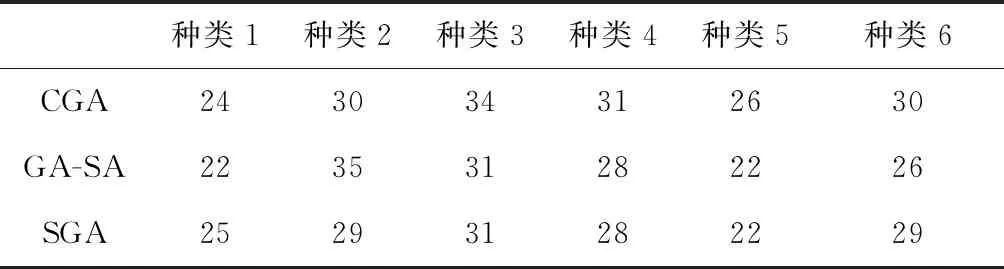
表3 基于Plant Simulation的仿真结果

5 结束语

以AGV作为搬运工具的智能车间在运行过程中具有明确的运行轨道及运行方向，因此通过传统的欧式距离和曼哈顿距离来计算物流成本，实现生产设备规划显然不合理。在以混合式机床设备配置的智能车间中，采用单向导引路径网络对AGV的搬运频率、单位距离成本、最短有向距离等参数进行优化，建立智能车间设备布局模型是一种可行的解决方案。本文在此基础上，将遗传算法与混沌映射算子相结合，提出一种混沌遗传算法来实现对基于优化路径的生产设备布局模型的解算。通过算法对比研究和平台仿真，结果均表明基于AGV单向导引路径网络的智能车间设备布局规划方法可以得到较为理想的布局方案。