随机利率下半连续型寿险产品定价分析

刘文文，文忠桥（安徽财经大学，安徽蚌埠233030）

一、引言

寿险行业是各种风险的集合地和分散地，不仅需要应对与其他行业相同的一般性风险，还要应对其特有的风险。随着寿险精算的不断发展和保险公司管理机制的提升，死差和费差带来的风险得到了很好的控制。但利率的变化无规律可言，因此利差成为影响寿险公司利润的最关键因素，利率风险是寿险公司最主要的市场风险。

1996年5月至2002年2月，央行连续八次调整基准利率，由以前的9.18%降为1.98%，使我国寿险行业第一次见识了“利差损”的强大威力。随后，经历了一段时间的统一预定利率后，我国于2013年开始进行费率市场化改革。2019年8月底，银保监会发布《关于完善人身保险业责任准备金评估利率形成机制及调整责任准备金评估利率有关事项的通知》（银保监办发〔2019〕182 号），该通知的实施将导致寿险行业需要增提1200 亿元的责任准备金，占责任准备金余额的1%。随着世界低利率时代的到来和我国资产收益率近几年持续下行，寿险公司中长期资产端的压力增大，该通知的实质是监管部门为了控制长期利差损风险，避免过高定价利率的同时提升准备金充足性，维护行业长期稳定发展。

寿险产品生命周期较长，在保单存续期间利率随时可能波动，寿险公司对利率变化异常敏感，因此对寿险产品合理定价是寿险公司经营中最重要的问题。传统的寿险产品采用固定利率进行定价，早就不能适应寿险公司的管理要求。因此，研究随机利率对寿险公司保费和责任准备金定价的影响，不仅符合目前我国利率持续下行的经济背景，而且符合“偿二代”以“风险”为导向的监管要求，还可以帮助寿险公司规避利率风险。此外，合理的定价也有助于寿险公司占有并维持一定的客户量。

国外通过随机利率进行保险定价的研究开始较早。Cox et al.（1985）在寿险公司利率风险的管理中引入单因子利率模型，提出了单因子免疫。William（2006）评估了准备金制度与利率通道之间的关系。Zaglauer and Bauer（2008）评估和分析了随机利率环境下人寿保险合同主要种类的担保和期权，对不同的期权元素使用蒙特卡洛和离散化方法来导出各自的值。Ming（2006）推导了随机利率环境下组合人寿保险收益的期望值和现值方差，提出了模拟利率过程和被保险人未来寿命的算法。国内相关研究起步较晚，赵静宇等（2008a）引入Vasicek 模型，利用蒙特卡洛模拟方法计算出随机利率下寿险产品的价格分布十分接近正态分布，反映了随机利率下寿险产品定价的合理性。同年，赵静宇等（2008b，2008c）利用CIR 模型评估随机利率，准确地计算了随机利率下的寿险责任准备金。孙娇娇（2019）利用Vasicek 模型，研究了欧式期权定价问题。张昌松（2014）运用标准模糊过程描述利息力函数，研究了模糊环境下的n年连续型生存年金计算公式，以及n年全连续型死亡保险的趸缴纯保费、均衡纯保费和准备金计提公式，并测算了常数利率、随机利率以及模糊利率三种环境下的数值。

综上所述，利用固定利率进行寿险产品定价存在诸多不足已经成为业内共识，大多数学者分别研究保费和责任准备金，但是这两者是不可分离的，低利率环境和监管要求若影响其中的一个，另一个也必然会受到影响。因此，本文针对n年定期缴费的半连续型终身寿险，结合保费和责任准备金定价进行建模分析，不再单一地分析保费或责任准备金，而是把整个保险流程的承保端与理赔端联系起来，更有利于寿险公司全面地考虑利差损带来的影响。本文主要分为两部分：第一部分随机利率建模，首先介绍Vasicek 利率模型，利用上海银行间同业拆借7日利率数据，使用广义矩估计方法估计参数，模拟未来利率的变动情况；第二部分寿险定价建模，首先计算固定利率下的年缴纯保费和责任准备金，然后分析随机利率下的年缴纯保费和责任准备金并与固定利率下的进行对比，从而得出随机利率定价的准确性和合理性。

二、Vasicek 模型实证分析

（一）Vasicek 模型概述

Vasicek 模型于1977年由Vasicek 提出，它是一种单因子模型，具体形式如下：

可整理为：

其中，r 为t 时刻的利率，α、-β、σ 都是大于零的常数，为布朗运动，ε服从标准正态分布；（α+βr）dt 为漂移项，σdw 为随机项；为短期利率的长期水平，即均衡利率，-β 为利率回复的速度，-β 越大，则随机利率r 向均衡利率回复的速度越快。当时，漂移项的符号为负，此时随机利率r 位于均衡利率上方，且r总体是向下移动的；当时，漂移项的符号为正，此时随机利率r 位于均衡利率下方，且r 总体是向上移动的。

由此可以看出，Vasicek 模型是一个满足均值回复特征的随机利率模型，这一特征是符合现实中经济活动特点的，当利率升高时，会导致资金需求减少，进而使利率下降，反之亦然。

（二）参数的GMM 估计

广义矩估计（Generation Method of Moments，GMM）是一种基于矩条件的参数估计方法，在金融领域中应用广泛。俞鹏程（2008）认为，与最小二乘估计和极大似然估计相比，广义矩估计更灵活一些。这里采用GMM 方法对上述Vasicek 模型中的3 个参数α、β、σ 进行估计。首先，对式（1）进行离散化处理得到离散化的Vasicek 模型：

其中，σεt为随机项，定义随机项为ζt，即ζt=σεt。由随机项的期望为0，得到方差为σ2的两个矩条件：

由于两个矩条件不足以估计3 个参数，我们利用工具变量zt=［1，rt-1］构造另外两个矩条件：

则共找到了四个矩条件：

这里的θ 代表要求解的参数α、β、σ。由于矩条件的个数超过了参数的个数，不可能找到合适参数使得所有矩条件都严格等于0，所以我们通过最小化如下函数来得到参数的最佳估计值：

其中，W 是权重矩阵，衡量各矩条件的重要程度。通常，W 的初始值设为单位阵，即开始时假设各矩条件具有相同的重要性。然后通过不断地迭代优化来得到最优的参数θ 和最优的权重矩阵W。

（三）数据及实证结果

1.数据选取与检验

随机利率模型建立过程中，虽然瞬时利率满足随机微分方程，但在现实金融市场中瞬时利率并不存在。因此，大多数学者采用短期利率来替代瞬时利率，最常用的利率品种即银行间同业拆借利率。拆借利率是根据市场上资金的供求状况而自由上下浮动的，也是发达货币市场上最基本的利率。目前，我国银行间的拆借利率是Shibor（Shanghai Interbank Offered Rate）。Shibor 的形成过程可分为三步：一是由信用等级较高的银行组成报价团；二是报价团成员自主报出同业拆借利率；三是计算第二步得到利率的平均值，这个平均值就是最终的拆借利率。根据拆借时长不同，Shibor 利率可分为8 种：隔夜（O/N）、1 周（1W）、2 周（2W）、1 个月（1M）、3 个月（3M）、6 个月（6M）、9 个月（9M）和1年（1Y）。

由于潘冠中（2004）证明了单因子利率模型参数估计数据选择的相关性原则，因此本文选择与其他利率短期变化相关性最高的利率作为瞬间随机利率rt的最佳近似替代利率。本文利用Excel 计算了8 个利率品种两两之间的相关系数，如表1所示，时间范围为2014年1月2日至2019年8月2日，数据来源于上海银行同业拆借利率官网（http：//www.shibor.org/）。由表1可以看出：相关系数最大的是0.99889（9个月与1年），相关系数最小的是0.62363（隔夜与1年），且这8 种利率之间都表现出强相关性且差距不大。随后，利用EViews10 软件对8 种利率数据分别做单位根平稳性检验。假设：所选取的数据序列有单位根，如果能拒绝原假设，即说明数据是平稳的。检验结果如表2所示。

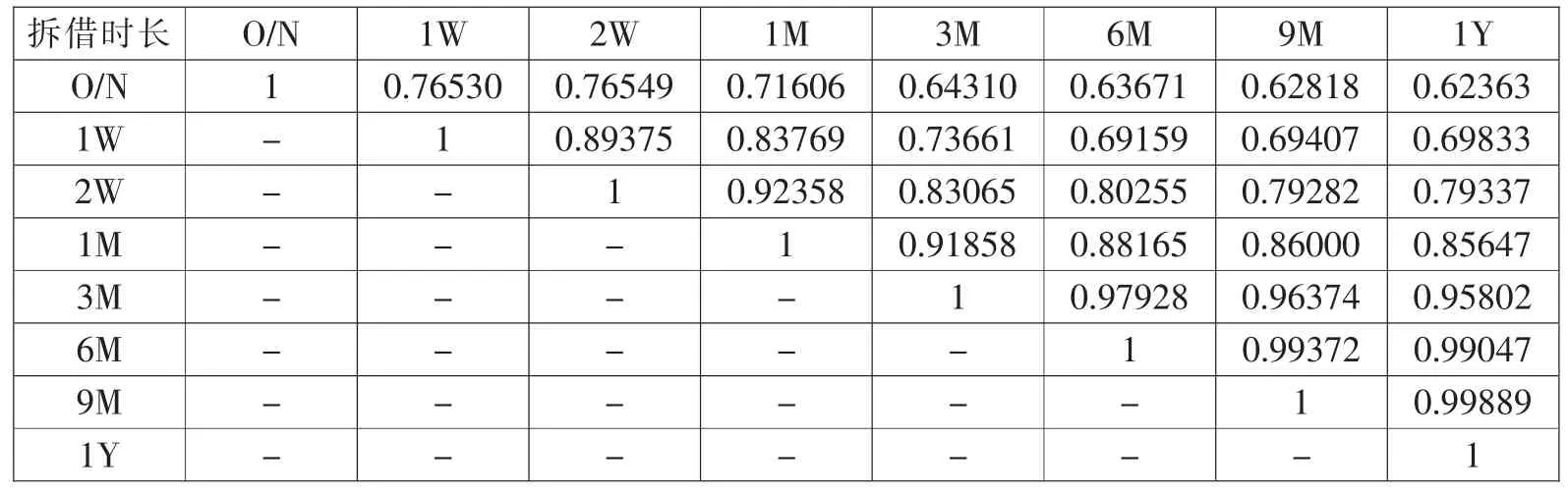
表1 Shibor 8 种利率之间的相关系数

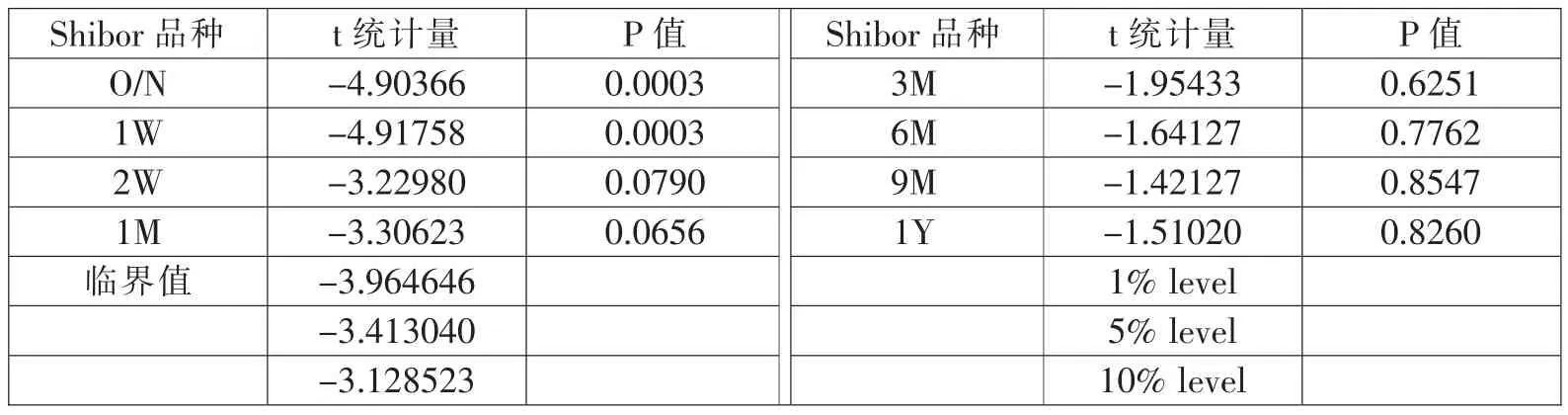
表2 Shibor 利率ADF 检验结果

由表2可以看出，3M，6M，9M，1Y 的t 统计量均大于显著性水平为10%的临界值，因此3 个月、6 个月、9 个月和1年的Shibor 数据存在单位根，接受了原假设，数据是不平稳的。O/N 和1W 的t 统计量均远远小于显著性水平为1%的临界值，因此隔夜和一周的Shibor 数据在置信度为99%的水平上不存在单位根，拒绝了原假设，数据平稳。结合相关性检验，隔夜和一周的拆借利率中，一周拆借利率与其他7 种利率的相关性更强，因此本文选择一周Shibor 数据进行参数估计。图1和图2分别绘制了2014年1月2日至2019年8月2日1395 个上海银行间同业拆借7日利率走势图及其一阶差分图。

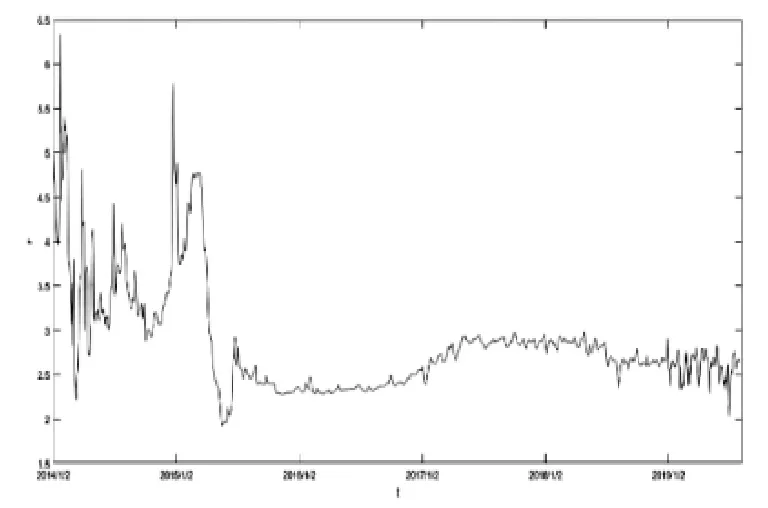
图1 利率走势图

图2 利率一阶差分图

从图1和图2可以看出，2014年全年的利率水平最高且波动最为剧烈，这可能与当年央行意外降息，五大民营银行获批等重大经济事件有关。2016-2018年利率相对比较平稳，而且利率波动是持续密集分布的，利率平稳时几乎没有波动，数据平稳。

2.Vasicek 模型参数估计

本文对Vasicek 模型进行广义矩估计的数学软件为Matlab，参数估计的结果见表3。

表3 Vasicek 模型参数估计结果

从表3中Vasicek 模型的参数估计结果可以看出，在0.05 的显著性水平下，α 和β 的t 统计量均大于临界值1.645（t 分布表）；在0.01 的显著性水平下，σ2的t 统计量大于临界值2.326，这说明参数估计值的显著性较高。此外，模型的χ2值越小，模型被接受的可能性越大，表3中的χ2值为3.95*10-13，由此可以推断出模型十分适合所选取的数据。根据表3的参数估计结果以及α=kμ，β=-k 可得到利用广义矩估计（GMM）估计出的Vasicek 模型为：

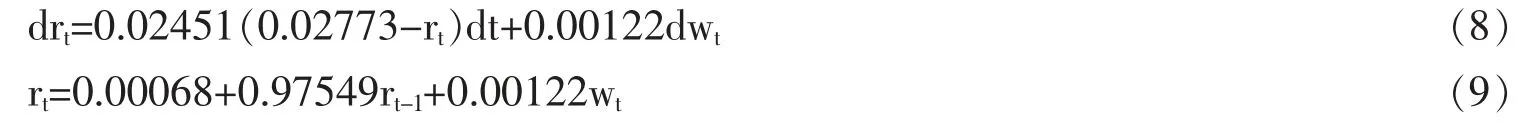
三、随机利率下半连续型寿险产品定价分析

杨浩（2017）认为，保险实务中半连续型寿险产品定价模型切合实际，可操作性比较强，是相对比较常见的保险模型。因此，本文实证分析保险定价和责任准备金定价都选择n年定期缴费的半连续型终身寿险产品。

（一）实例假设

根据《人寿保险精算规定》，我们对相应的参数进行适当的假设。假设条件如表4所示。

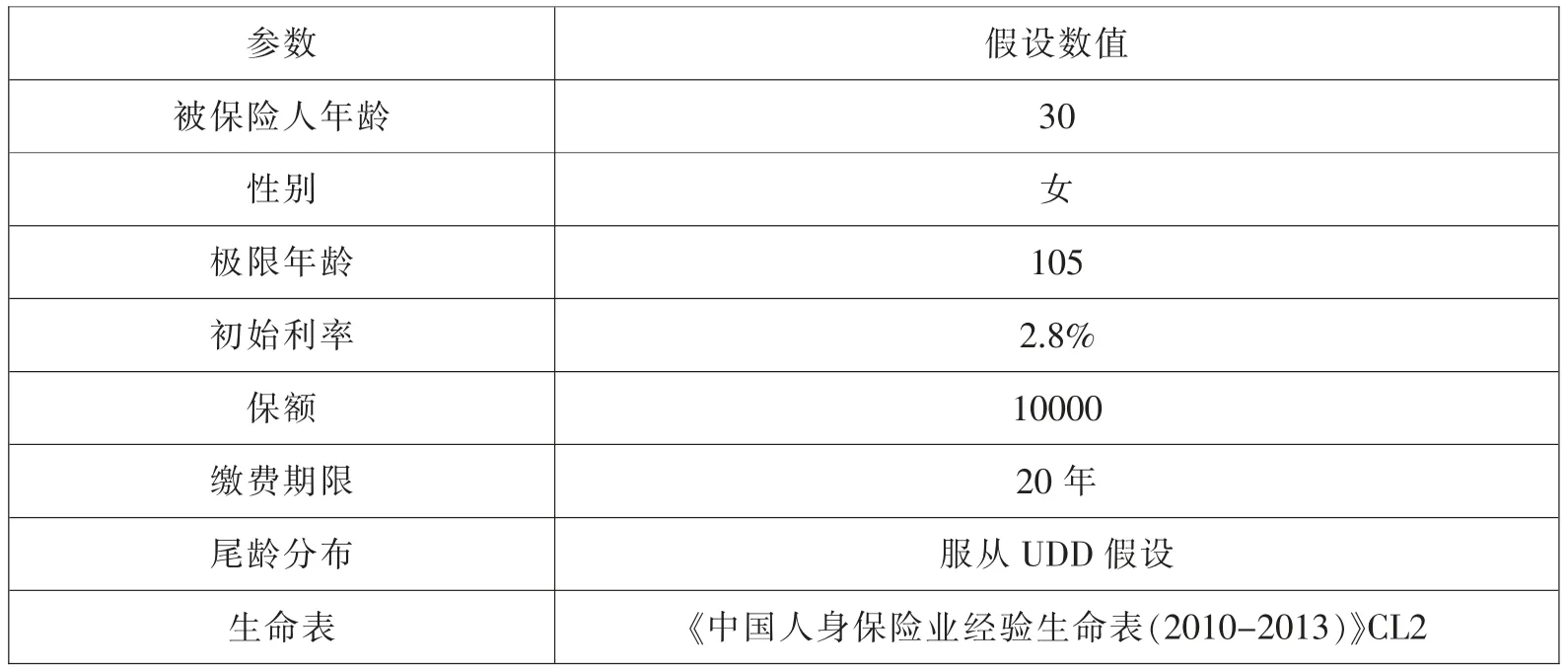
表4 相关参数假定

（二）年缴纯保费定价分析

人寿保险主要采用均衡保费法缴纳保费，绝大多数投保人采用分期缴费的方式，以避免一次性缴费造成的经济负担，如按年缴纳的纯保费，称为年缴纯保费。

1.固定利率下的年缴纯保费

固定利率下终身寿险的半连续型年缴纯保费定价公式为：

2.随机利率下的年缴纯保费

将式（10）中的v 替换为随时间变化的折现因子vt，就可以得到随机利率下的n年定期寿险的年缴纯保费定价公式，折现因子，rt服从Vasicek 利率模型，其迭代公式由式（9）给出。

前文所得到的半连续型年缴纯保费定价模型形式复杂，很难对其经验分布函数图进行模拟。为了解决这个难题，我们选用蒙特卡洛方法，结合Matlab 软件中的Randn（）函数来实现。

下面利用蒙特卡洛方法，结合Vasicek 模型，使用Matlab 软件计算，具体步骤如下：

第一步，使用Matlab 中的Randn（）函数生成10000 个dWt序列，t=1，2，3，…，n，dWt服从标准维纳过程。

第二步，将生成的dWt序列代入式（9），生成10000 条利率路径rt，t=1，2，3，…，n，如图3所示。

第三步，将生成的利率路径rt代入随机利率下年缴纯保费定价公式，生成10000个年缴纯保费值kP（），如图4所示。

第四步，根据生成的kP（）的模拟值得出年缴纯保费的经验分布函数以及相关统计数据，如表5和表6所示。

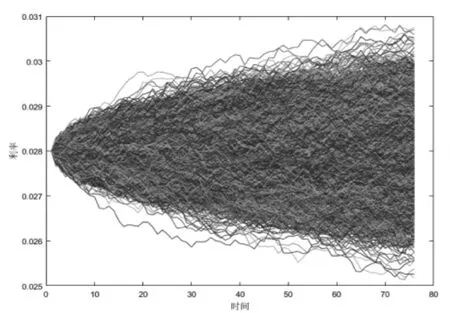
图3 利率路径图

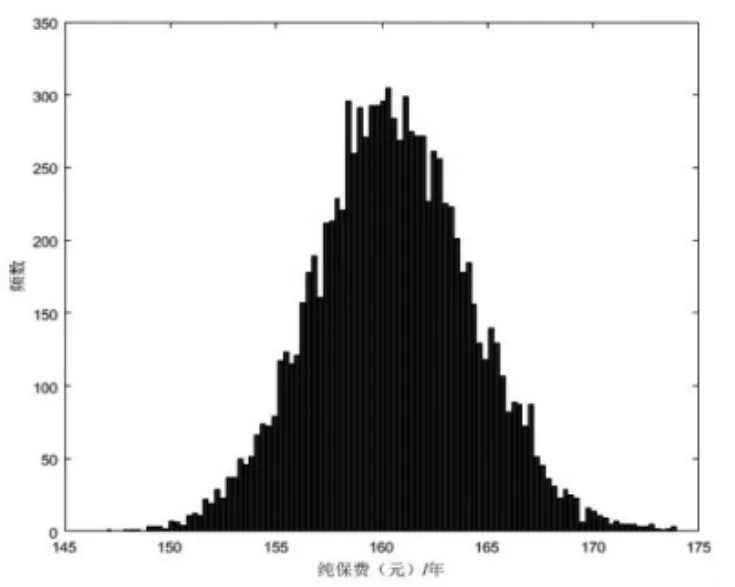
图4 年缴纯保费分布

表5 相关统计量

表6 定价分位点

由表5和表6可知，随机模拟的年缴纯保费的最小值为147.899 元，最大值为177.179 元，平均值和中位数非常相近。价格定位点显示90%的置信区间是［154.727，166.755］，偏度为0.085＞0，分布具有正偏离，但偏离程度非常小。由图4可以看出，模拟的年缴纯保费曲线比较对称、接近于正态分布，主要集中在155～165，中位数对应的价格正好在50%的分位点上。

固定利率下的年缴纯保费是160.547 元，非常接近随机利率下的中位数和平均值，这是因为固定利率下定价采用的利率2.8%为1395 个利率的均值。由于模拟次数的限制和随机数的任意性，两者会存在偏差，但结果显示这个偏差是很小的。随机价格的均值高于固定利率下价格，可以看出均值位于70%～80%的分位点所对应的价格之间，用均值160.64 元定价更加安全、合理。虽然相对略高的价格增加了投资人的投资成本，但却提高了保险公司的偿付能力，使保险公司更加安全，所以我们推荐用均值定价。

（三）责任准备金定价分析

责任准备金是指寿险公司为了在未来的某一天给付被保险人的债务，提前提存的不能用于投资的款额。

1.固定利率下的责任准备金

假定初始利率为2.8%（即1395 个随机利率的均值），可以得到假设案例中固定利率下半连续型终身寿险的责任准备金的简约计算公式为：

其中，k 为保单年度，根据以上公式，可以计算得出不同保单年度下的寿险责任准备金，计算结果如表7所示。

表7 分年度准备金

2.随机利率下的责任准备金

同样地，将固定利率下的半连续型n年定期寿险的年缴费情形下的责任准备金的计算公式中的固定折现因子v 替换为时变折现因子vt，得到随机利率下责任准备金的计算公式是：

图5 基于Vasicek 模型的10000 次模拟的准备金数值分布

表8 相关统计量

表9 定价分位点

由表8和表9可知，随机模拟的责任准备金最小值为4775.719 元，最大值为5832.582 元，固定利率下第30年年末的责任准备金为5294.015 元。价格定位点显示90%的置信区间是［5062.470，5533.582］，偏度为0.097＞0，峰值为2.992，非常接近3，由此可见，准备金的分布接近正态分布，分布具有正偏离，但偏离程度非常小。一般情况下，准备金数额定在60%至95%的分位点之间。比如取70%的分位点的额度时，与固定利率相比，则多提取的准备金是5368.386-5294.015=74.371 元，不过这不能说明2.8%的固定利率下评估的准备金是不充足的。本文只是提供在利率随机变动的条件下评估准备金的一种方法。由于固定利率下的责任准备金与随机利率下的均值、中位数都非常接近，因此本文建议采取随机利率下的均值和中位数进行准备金定价。

四、结论

寿险公司会受到未来一定时期内市场利率上下波动的影响，单纯利用固定利率进行保险产品费率的厘定已经不能满足寿险公司偿付能力的要求。由上述实证结果可以看出，模拟的年缴纯保费和责任准备金分布均接近正态分布，说明利用随机利率进行寿险产品的定价，不仅准确性和稳定性更高，而且可以给予寿险公司更多可供参考的数据。当前低利率环境下，无论是银保监会2019年182 号文件要求准备金评估利率上限调整为3.5%，还是监管部门从2018年开始就很少再批复高预定利率的产品，都在提醒寿险公司需注意利差损带来的经营风险。寿险公司应该摒弃固定利率的定价方式，利用随机利率进行科学定价，这不仅符合当前的监管要求，还可以帮助寿险公司合理定价，规避面临的利率风险，最重要的是能在利率下行导致投资收益减少、资产端压力增加的情况下，从源头控制负债端，减少寿险公司的未来负债，使寿险产品的高预定利率成为历史。未来进一步研究的方向是：考虑持续的低利率环境下，利率变动对寿险公司一些新型寿险，比如分红险、万能险和投资连结险的定价和投资收益的影响。