正弦波纹挡板式沉降器内流动特性

张玉辉，龚斌，王学平，张静，吴剑华

（沈阳化工大学辽宁省化工新技术转移推广中心，辽宁沈阳110142）

随着国内外油田采出液含水率的逐渐上升、含油污水处理难度的逐步增大，紧凑高效油水分离设备的开发已经迫在眉睫。重力沉降油水分离是非均相液液物系分离的重要手段，广泛应用于石油、化工、环保等行业，已由最初的单层撇油池、自然沉降罐、加热沉降罐、化学沉降罐、电脱水沉降器等发展到现今各种多层水平平板、多层平板及多层斜板等内部多层分离构件的新型沉降器。其中，多层斜板重力沉降器是重力沉降器的代表形式，具有处理量大、操作灵活、占地面积小等优点[1]。

为保证重力式多层斜板沉降器的分离效率，斜板组分离区内部流场应尽可能达到或接近柱塞流。一般的做法是放置入口构件[1]，用以吸收进入设备液流的动能，减小进液口射流对防冲挡板后部区域流场的冲击。近几十年国内外学者对多种形式入口构件进行了大量分析比较。其中一类是上孔箱式[2-4]、下孔箱式[2,5]、圆形分散孔式[6]等带孔形式的入口构件，如陆耀军等[2]采用粒子图像测速（PIV）系统证明了下孔箱式入口构件不仅可以获得速度较均一的流体，还起到一定的预分离作用；李振林等[3]将上孔箱式入口构件改为通过圆筒形式，并从沉降器底部进液，混合液再经布液器进入沉降器，有效减小了进液的动量；江朝阳等[6]首次采用圆孔分散式入口构件，利用响应面分析法对其进行了优化。王振波等[7]将整个平挡板上开设圆孔，解决了挡板后涡流掺混严重的问题，有效降低了油水混合相的紊乱程度。虽然带孔式的入口构件能够有效降低流体湍动、缓解返混现象，但由于非均相物系往往含有固体颗粒、沥青质、絮状物等活性物质，孔隙很容易被堵塞造成分离效果下降、泵电机的损坏；另一类入口构件是板式入口构件，如平挡板[2,8-9]、凹面式[8,10-11]、凸面式[8,11]、蝶式[2]等。王学平等[10]在沉降器进口处放置方形平面防冲挡板，通过Fluent软件模拟表明：冲击间距对流型的影响很大，同时挡板四周的流通面积为30%条件下，沉降器内流体速度和湍流强度的衰减最快；张静等[11]分析了平面、凹面、凸面共3个类型的入口构件对流场的影响，结果表明：入口构件的曲率对流场存在较大影响。Ye 等[12]提出了一种折流进液方式，通过与无挡板沉降器的对比，新式挡板可以增加液相的停留时间，减少水相中的夹带。挡板式入口构件无堵塞情况，但普遍存在返混和短路现象，设备空间未能有效利用。事实上，除了入口构件的形式，沉降器形式、挡板位置、进液口高度等因素均都会对沉降器的处理能力和分离性能产生很大的影响[10,13-16]，如Asgharzadeh 等[13]利用声学多普勒技术（ADV）对挡板排列方式、挡板位置、挡板高度进行了优化，得出放置合适高度的挡板可以有效提高沉降器的分离效率的结论；Tamayol 等[14]模拟了进口位置对沉降效果的影响，研究发现沉降器内挡板可以有效减弱死区的影响，并且挡板位置存在较优值。

作为应用最广泛的入口构件，平挡板虽然可以有效避免非均相流体中活性物质堵塞挡板孔隙。但由于其基本没有整流功能，造成流向速度分布不均匀，挡板后会形成严重的一次涡流，局部区域中还伴随有不同程度的二次涡流[1,4]。为了缓解这种不利情况，本文将挡板由平面改进为正弦波形，提出一种新式防冲挡板——正弦波纹挡板，增强入口构件的整流效果。分析了正弦波纹挡板作为入口构件的可能性，并对其时间特性和空间分布特性两个方面进行分析，探讨了冲击间距对沉降器分离性能的影响，为流体能够在分离区保持均匀稳定、提高分离效率提供参考。

1 计算方法与验证

1.1 物理模型

图1 设备尺寸立体示意图

物理模型结构和尺寸参数如图1所示。沉降器为长方形槽体，流体从进液圆管进入，从正弦波纹挡板两侧流过，进入沉降器的斜板组，最后经由溢流堰流出。入口流量Qin=2m3/h。沉降器槽体长（X方向）×宽（Y方向）×高（Z方向）为880mm×300 mm×380mm，沉降器进口圆管直径D=30mm。挡板采用正弦波形式，波距和波高λ=2A=30mm，斜板组中斜板厚度均为2mm，间距为40mm，具体参数见图1(b)。溢流堰高度为300mm，沉降器上部初始条件为80mm的空气层。当非均相物系中离散相的含量小于5%左右时，相间滑移对流场影响可以忽略，只采用连续相进行模拟也可以得到与实际情况符合较好的结果[14,17-19]，所以本文采用单相-水进行模拟。

1.2 模拟方法

应用计算流体动力学软件Ansys Fluent 16.2 进行数值模拟。采用两相流VOF 模型模拟带有自由液面的流场变化。在每个控制体内，所有相的体积分数αq之和为1，通过对第q 相的体积分数的连续性方程求解，可以实现对两相界面的跟踪。第q相方程式见式(1)[20]，动量方程见式(2)。

式中，αq为第q 相的体积分数；ṁpq为传质速率，进入q 相时的传质速率为正，离开q 相时的传质速率为负；n 为相数；Sq是进入q 相的外部质量源；ρ 为混合密度，ρ =∑αqρq；μ 为混合黏度，μ =∑αqμq；表面张力和壁面黏附通过动量方程中的附加源项引入。

湍流模型采用Realizable k-ε模型[21-22]，湍流模型中近壁面采用Scalable Wall Functions算法；压力和速度的耦合采用PISO 算法，压力的离散采用Body Force Weighted 格式，动量、湍动能、湍动能耗散率均采用Second Order Upwind格式离散。

在模拟过程中，首先初始化Z/D=1～10部分为水、Z/D=10～12.6部分为空气，对沉降器内流场进行稳态计算，当出口的质量流量波动小于0.1%时，继续迭代1500 步完成稳态初始化流场。将稳态计算结果作为非稳态计算初始流场，计算收敛条件为连续性方程收敛残差为10-4，其余变量收敛残差为10-5。

1.3 计算方法验证

本文在Ansys ICEM 软件中采用六面体网格对模型进行划分。为保证网格质量，正弦波纹板附近的网格采用Y 形划分策略，并对该区域进行加密。网格的雅可比行列式值最小为0.594，96.6%的网格结果大于0.8，网格角度最小为20.25°，91.11%的网格角度超过63.22°，最大纵横比为14，网格纵横比超过5.75的网格仅占总网格数的3.80%。通过上述评价指标可知网格划分合理[23]。

为验证网格尺寸对模拟结果的影响，选取不同网格尺寸的4套网格方案，具体参数见表1。图2(a)为Lb/D=2.17，Lw/D=2.5的条件下误差分析结果，不同网格方案在X/D=1.67、Y/D=5.0 处Z 方向的沉降器轴向流速的误差随着网格总数的增加，整体呈现逐渐下降的趋势。当3#网格方案的网格数为108.3万，与4#网格方案的平均偏差为2.70%，最大偏差为9.27%。对于湍流流动，近壁面网格质量可以通过Y+值进行评价[24]，3#网格方案正弦波纹板近壁面区域的Y+平均值为4.96，Y+＜10 的网格超过89.55%。综合考虑计算精度和计算时间，选择3#网格方案对模型进行划分。

表1 不同网格尺寸划分方案

在3#网格方案的基础上，采用相同条件进行时间步长无关性验证，时间步长选择t=0.1s、0.05s、0.01s、0.005s，结果如图2(b)。结果表明：速度分布与图2(a)基本一致，随着时间步长的减小，平均偏差和最大偏差都呈现减小的趋势，其中时间步长为t=0.01s 和t=0.005s 的平均偏差为0.50%，最大偏差为3.74%，故时间步长选择t=0.01s。

1.4 模型检验

由于实验条件的限制，本文建立了无斜板组的实验装置，如图3所示，并按相同的物理结构、几何尺寸建立用于数值模拟的模型，保证数值模拟与实验的一致性。通过数值模拟所得的进口区域展向速度分布与TR-PIV 测量的实验结果进行对比，用以验证所选计算模型的准确性。为保证拍摄效果，沉降器采用厚度为10mm的有机玻璃，离心泵型号为TYP.MHI202-1，最大流量为5m3/h，实验过程中，通过调节球阀的开度来控制流量。实验采用的TR-PIV系统为丹麦Dantec 公司生产，采用空心玻璃珠作为示踪粒子，密度为1.1×103kg/m3，平均直径为10μm，根据Stokes 公式计算得到的沉降速度为6.1×10-5m/s，实验装置内流速在10-2m/s 的量级上，故由沉降作用引起的实验误差基本可以忽略。图像后处理采用16×16 pixel大小的查问域对粒子图像进行互相关分析，计算得到98×87个矢量。

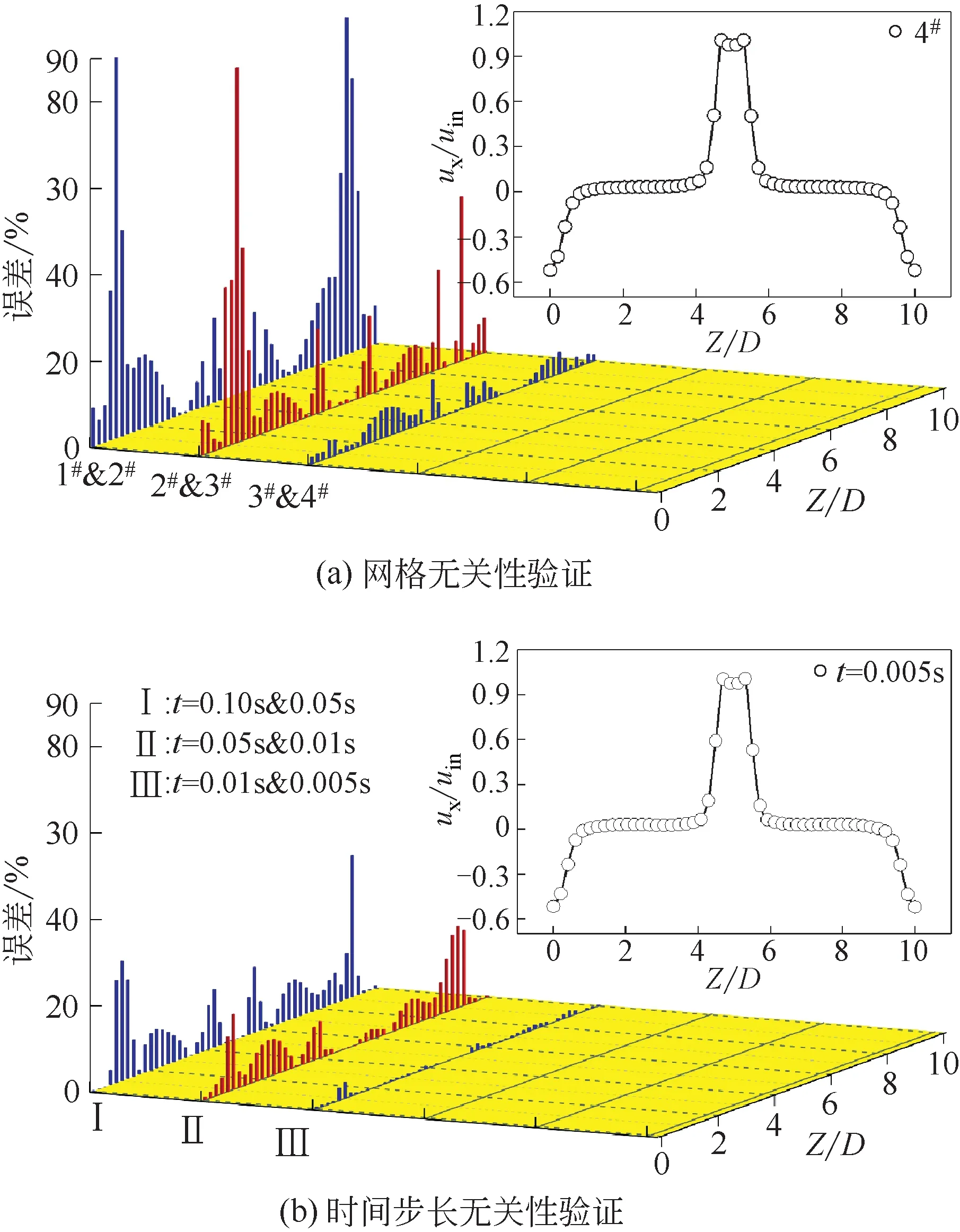
图2 无关性验证

图3 实验装置示意图

图4 模型有效性验证

图4 为X/D=1.67、Y/D=5.0 处Z 方向的沉降器轴向速度分布情况，数值模拟结果与TR-PIV 测量结果吻合较好，再现了进口射流冲击正弦波纹板的轴向流速分布，但存在一定偏差，分析其原因在于：第一，TR-PIV 测量过程中片光源与待测平面不可避免的存在偏差；第二，实验中使用离心泵对流体进行输送，进口流量存在一定的脉动，湍流强度无法控制，而数值模拟采用均一速度入口。综上所述，本文所建立的数值模型和模拟方法是可靠的，可用于沉降器内流场的研究。

2 模拟结果与讨论

2.1 流场结构分析

图5 截面Z/D=5.0处平均速度场

图5为冲击间距Lb/D=2.17情况下不同形式挡板的截面Z/D=5.0 处的平均速度场分布。从图5(a)平挡板左侧的入口区域流线图可以看出，流体冲击平挡板使流动方向发生改变，并随后冲击在沉降器两侧壁面，平挡板前形成了一对对称分布的涡旋；而图5(b)中的流线分布表明正弦波纹板前的流体没有与壁面剪切形成大尺度涡旋，挡板的整流作用明显高于平挡板，这是由于流体冲击正弦波纹板褶皱时产生的涡旋使湍动能得到充分耗散。平挡板后的平均流向速度呈对称分布的特点，在2＜Y/D＜8的范围内，挡板尾流的ux/uin为负值，这表明沉降器内存在明显的返混现象，随着X/D的增加，返混情况改善，但始终存在于沉降器内部，如图5(a)所示。而图5(b)中正弦波纹挡板后ux/uin的分布相对均匀，其值均为正值，表明流场无返混现象，有利于液-液分离过程的进行。截面X/D=8.0 为斜板入口区域，对评价入口挡板作为入口构件具有重要意义，采用平挡板时，截面上平均流向速度ux/uin的极差值为0.1625，是正弦波纹板的6.5 倍，所以正弦波纹挡板可以有效提高流场速度的均一性。

2.2 时间特性分析

沉降器轴向速度均一程度的分析对优化入口构件尺寸参数和提高沉降器的分离效率具有重要意义。取截面X/D=8、11、18、25的轴向速度均一度的时间演化情况分析。计算方法采用陶红歌等[28]基于面积加权平均速度和质量加权平均速度提出的计算关联式，见式(3)。其中，Va为基于面积加权平均速度；Vm为基于质量加权平均速度，计算式见式(4)、式(5)。

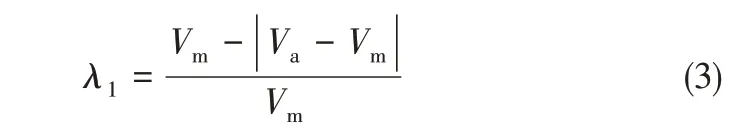
式中，A为总面积；vj表示第j个单元上的速度矢量；Aj表示第j 个单元上的面积矢量；ρj表示第j个单元上的流体密度；n为划分单元的个数。

该方法是基于不同加权方法获得的评价指标，与采集点分布形式、个数都没有关系，因此能够更准确地对流场均匀性做出评价。λ1取[0,1]，λ1越大则流动均匀性越好，1 表示理想状态下均匀流动。图6(a)、(b)分别是平挡板和正弦波纹挡板在Lb/D=2.17 情况下，4 个截面（X/D=8、11、18、25）的λ1随时间演化情况，两种情况的λ1均存在明显的波动，平挡板条件下λ1在0.21～0.58波动，而正弦波纹挡板由于涡旋的形成，使λ1波动范围增加至0.3～0.71，相同截面的正弦波纹挡板的λ1值明显高于平挡板。当采用正弦波纹挡板作为入口构件，Lb/D从2.17 减小至1.5 时，λ1值的波动呈现下降趋势，其中截面X/D=11 的λ1均方根降低了21.97%，这可能与流动形式改变有关，同时表明冲击间距的减小提高了流场稳定性，如图6(b)、(c)所示。图6(d)、(e)表明随着Lb/D的减小，λ1波动进一步降低，其数值也整体呈现下降趋势，所以在一定范围内，过小的冲击间距对于提高流场速度均一程度是不利的。

图6 轴向速度均一程度随时间演化情况

2.3 空间特性分析

图7为Lb/D=2.17、1.5、0.84情况下，沉降器内轴向速度均一度沿流动方向的空间分布情况。由于正弦波纹挡板长度直接影响了流体的流通面积，研究了挡板两侧流通宽度Lw/D=2.5、1.5 对沉降器轴向速度均一程度的影响。图7(a)中对比正弦波纹挡板和平挡板曲线可以发现：在相同Lw/D条件下，正弦波纹挡板的λ1均高于平挡板。正弦波纹挡板的Lw/D=2.5 比Lw/D=1.5 更有利于提高λ1，因为更大的流通面积可以降低流体与壁面的剪切作用；当Lb/D=1.5、0.84 时，两种挡板形式情况下，不同的Lw/D取值对λ1影响很小，尤其X/D＞15时，流体受到斜板的整流作用，λ1值差异进一步减小，如图7(b)、(c)所示。值得注意的是，在X/D=10.0～12.0处，即斜板组的进口位置区域，平挡板的λ1呈现先上升后下降的趋势，这是由于流体在进入斜板组时，平挡板后侧的对称回流涡旋冲击斜板组，流场复杂程度增加，使得λ1呈现下降趋势，而波纹挡板尾流没有双子涡旋，流体以类柱塞流形式进入斜板组，所以在斜板组进口区域的λ1无明显下降趋势。

沉降器具有较好分离效果不仅需要均匀的轴向速度分布，轴向速度的波动程度还应尽可能的小。为定量说明沉降器内不同截面上流体的轴向流速平均波动程度，引入评价指标：基于面积加权平均的湍流强度Ia，见式(6)。

式中，Ij为截面上j处的湍流强度。

通过比较不同工况下的Ia值可以评判截面上流场轴向速度的波动程度，Ia值越小，波动程度越低。由图8中可以看出，经过挡板后Ia呈现下降趋势，平挡板的Ia总体高于正弦波纹挡板，这是由于流体在正弦波纹板褶皱产生涡旋，湍动能得到充分的耗散，而平挡板仅起到改变流体流动方向的作用，流体湍动能集中，不利于分离的进行。随着X/D 的增加，平挡板和正弦波纹挡板的Ia差异性均呈现减小的趋势，当X/D＞20时，Lw/D对流场湍动强度无明显影响，这是因为流体在斜板组内被进一步整流，流场稳定性提高，湍动能的耗散能力相差不大。

为探究正弦波纹挡板沉降器内流场均一程度较平挡板提高的机理，选取冲击间距为Lb/D=2.17 的截面X/D=8.0 进行分析。图9(a)为平挡板截面处的轴向平均速度云图，截面整体呈现很大的速度梯度，在四个顶角处各有一个轴向速度的极大值，截面中部存在很大的负速度区，造成了返混，轴向速度分布很不均匀。图9(b)为正弦波纹挡板截面处的轴向平均速度云图，速度为-0.01～0.04m/s，其范围较平挡板明显下降，负速度区面积明显减小，有利于后续分离操作的进行。

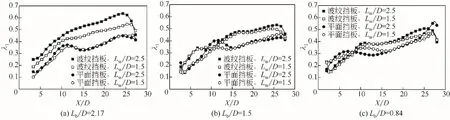
图7 轴向速度均一度的空间演化情况分析

图8 基于面积加权湍流强度的空间分布情况

图9 截面X/D=10的轴向平均速度云图

图10 为50 个瞬时流场进行均方根运算用以表征截面上轴向速度波动的分布情况，计算见式(7)。

式中，Urms,i为截面上i 点的速度均方根；ui,k为截面上i点第k个时刻的轴向速度；-ui为截面上i点的轴向平均速度；N=50。

图10 截面X/D=10轴向速度均方根云图

对比图9 与图10 可知，Urms值分布云图与轴向平均速度分布云图基本一致，这是因为速度较高的位置与涡旋的位置相差不大，涡旋的不稳定性导致了Urms的较大值。其中正弦波纹挡板的Urms梯度主要位于沉降器中部，最大值为0.07。与平挡板相比，正弦波纹挡板的Urms最大值明显降低，流场稳定性提高。

2.4 冲击间距对流场的影响分析

重力式斜板沉降器内轴向流动状态是考察流场分离性能的重要指标，轴向流速越均匀说明越接近水平柱塞流，对非均相物系的分离越有利，前人对流场分离性能的研究主要以此为基础[4,6,8]。但是为了保证较好的分离效果，沉降器内轴向流速除了保证较高的均一程度，其波动程度还应尽可能低，这样才能保证对离散相的扰动更小，获得更好的分离效果。结合沉降器内轴向流速脉动程度和流速均一性对流场分离性能评价的相关研究鲜有报道，现有研究方法对流场分离性能评价还不够全面。

本文类比战洪仁[29]提出的对流强化换热评价方法，引入了流场均稳指标（uniform&steady criteria，USC），计算见式(8)。

式中，λ1,0为无挡板情况下截面的轴线速度均一度；Ia,0为无挡板情况下截面的基于面积加权平均的湍流强度。

USC 为量纲为1 的量，其数值大于1 时，说明在相同条件下正弦波纹板沉降器的流场分离性能优于无挡板情况。USC的数值越大说明流场对分离过程的进行越有利。图11(a)为Lw/D=2.5情况下冲击间距对USC 的影响。可以看出曲线呈多峰分布，峰值极大值位于Lb/D=2.17 处，并且随着X/D 的增加，USC值呈现增大趋势，说明流体受到入口效应的影响减弱。其中截面X/D=25取得极大值14.68，比次高峰高出15.89%，相同条件下平挡板的USC 值为7.58，正弦波纹挡板较平挡板提高了93.67%。图11(b)为Lw/D=1.5条件下的冲击间距Lb/D对USC值的影响情况，Lb/D=2.17 时取得极大值10.96，相同条件下平挡板的USC 值为7.41，为正弦波纹板的65.14%。综上分析可知，正弦波纹挡板可以有效提高流场分离性能；在现有数据的基础上，应选择冲击间距为Lb/D=2.17 进行后续研究，同时增加对含有离散相的混合物流场特性研究，使流动特性结果更加全面、具有说服力。

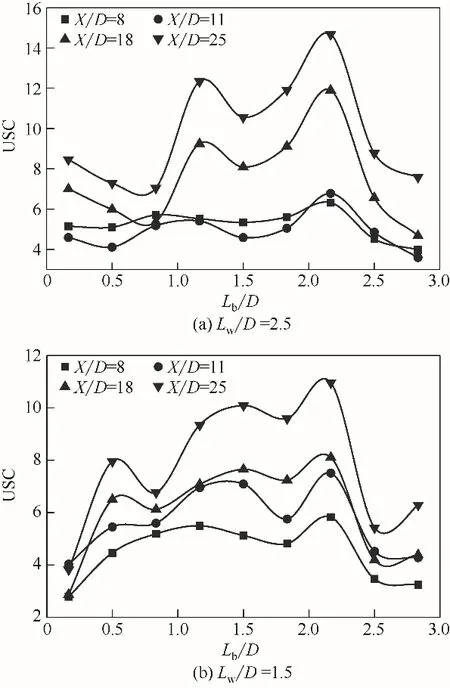
图11 冲击间距对USC值的影响

3 结论

（1）正弦波纹挡板沉降器内流动相对稳定，尾流速度分布相对均一，作为入口构件是可行的。

（2）平面挡板和正弦波纹挡板的λ1均有较大波动，其中正弦波纹挡板的λ1波动极差达到0.31；当冲击间距Lb/D 小于1.5 时，正弦波纹挡板的λ1相对稳定。

（3）正弦波纹挡板沉降器在Lw/D=1.5 和2.5 情况下的λ1均高于平挡板，具有优良的适用性。

（4）正弦波纹挡板沉降器内流向截面的Ia总体低于平挡板沉降器。当Lb/D=2.17 时，正弦波纹挡板与平挡板沉降器Ia最大差异为45.10%，随着冲击间距的减小，Ia差异逐渐减小。

（5）与平挡板相比，正弦波纹挡板在截面X/D=10 处轴向速度范围降低了58%，沉降器两侧壁面附近的速度梯度明显降低，回流区面积和负方向速度均减小。同时正弦波纹挡板可以使轴向速度波动明显降低，流场稳定性得到一定的提高。

（6）随着冲击间距的增加，USC呈现多峰分布趋势；当Lb/D=2.17 时，流场分离性能可以取得较优结果，USC 极大值为14.68，相较同条件下的平面挡板提高了93.67%。

符号说明