多传感器箱粒子PHD滤波多目标跟踪算法

蔡如华，杨 标，吴孙勇,2

（1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.广西密码学与信息安全重点实验室，广西 桂林 541004）

0 引言

多目标跟踪（multi-target tracking,MTT）算法的有效性和实时性一直以来是国内外学者关注的热点。针对多目标跟踪问题，Mahler 提出了随机有限集[1]（random finite set,RFS）理论，将多目标状态集和多目标观测集建模为随机有限集的形式，有效地解决了基于多假设跟踪[2]和联合概率数据关联[3]在多目标跟踪过程中产生的组合爆炸问题，并提出了基于随机有限集的概率假设密度[4]（probability hypothesis density filter,PHD）滤波器，PHD滤波器能够对目标状态和数目进行有效的估计。

传统的粒子滤波器是以点粒子的形式来模拟目标状态。在进行蒙特卡洛实验时，需要大量的点粒子来对目标进行捕获和持续跟踪，所以会产生较大的计算量，为减轻计算量，文献[5]提出了基于区间分析[6-7]的箱粒子滤波算法，之后在文献[8]中结合PHD滤波器实现了箱粒子PHD滤波器，从而减轻了计算量。2015年国内学者宋骊平[9]将箱粒子PHD滤波用于扩展目标跟踪，之后在文献[10]中使用箱粒子PHD滤波对群目标进行了有效的跟踪。文献[11]提出了未知杂波状态下基于箱粒子滤波的PHD算法。

但对于低可观测目标的跟踪，单传感器PHD滤波器已不能满足需求，而多传感器技术的应用则能够很好地解决这一问题。早在2009年，Mahler[12-13]便给出了多传感器的实现。文献[14-15]分别给出了多传感器PHD滤波的序列蒙特卡洛实现和高斯实现，文献[16]利用先验信息对下一时刻可能存在目标的区域进行压缩，并利用多个被动式传感器同时对可能存在目标的区域进行观测，以多个被动式传感器的观测角度相交区域以及传感器位置计算得到目标位置区间，作为目标区间量测，根据区间量测值产生箱粒子，再利用箱粒子PHD滤波对目标进行跟踪，旨在去除虚假量测降低运算量，提升计算效率。

本文则是针对低可观测目标难以跟踪以及点粒子滤波产生较大计算量的问题，利用多传感器技术在低可观测目标检测上的优势以及箱粒子滤波能够提升计算效率的优势，提出MS-BOX-PHD算法。并通过仿真实验验证了MS-BOX-PHD算法对多目标状态以及数目估计的稳定有效性，以及MS-BOX-PHD算法相对于区间量测下多传感器标准PHD 粒子滤波（multi-sensor standard probability hypothesis density particle filter with interval measurement,IM-PHD-PF）算法在计算效率上的优势。

1 系统模型

在多目标跟踪系统中，会有多个目标随机的出现和消失在观测区域中。全文单目标状态用小写字母x表示，其中(x,y)包含目标位置信息，包含目标速度信息；多目标状态用大写字母X表示；单目标量测用小写字母z，z= [θ;r]，其中θ表示角度，r表示距离；多目标量测集用大写字母Z表示。

1.1 多目标状态转移模型

考虑系统：

式中：k为时间指标；f为非线性的状态转移函数；wk表示k时刻的过程噪声。对于k时刻多目标状态可以描述为随机有限集：

式中：N表示k时刻的目标个数。xk,i表示k时刻的第i个目标，可能为新生目标，也可能为k－1时刻存活并转移后的目标。

1.2 多目标多传感器量测模型

对于k时刻的目标xk,i，其可能被传感器检测到并产生量测值zk,i，也可能未被传感器检测到，没有产生量测值，同样在k时刻传感器也可能产生虚假量测。

由第s∈{1,2,…,S}个传感器产生的量测集合Zks可表示为：

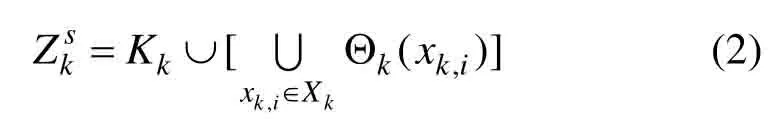
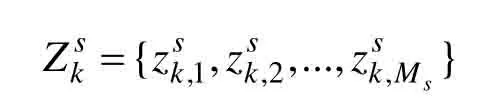
本文采用非线性量测模型，假设第s个传感器位置为(dxs,dys)，则量测方程为：

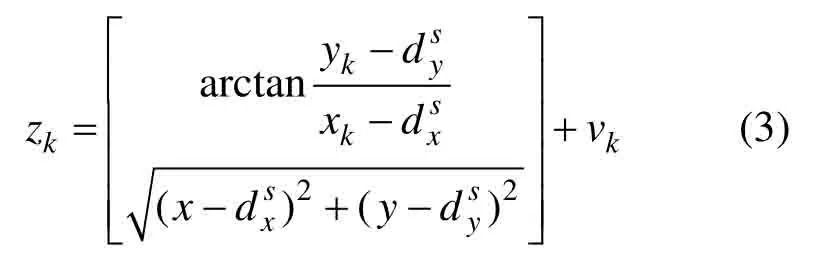
2 收缩算法

收缩算法以区间分析[6-7]为基础，通过区间收缩，保证更新之后的箱粒子拥有一个合适的区间大小，并利用收缩前后的箱粒子区间大小来求解似然函数，从而对箱粒子的权重进行更新。

假设原箱粒子为[x]，区间量测值记为[z]，h为量测方程，若则[x′]＝[x]，但是似然度否则收缩后的箱粒子满足：

收缩之后得到的箱粒子[x′]的似然度可以表示为：

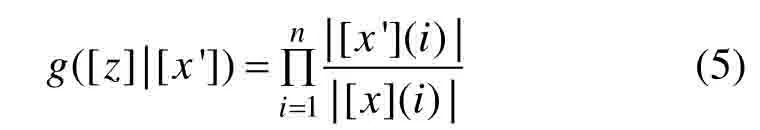
式中：|[⋅](i)|表示箱粒子[⋅]的第i维的长度。

3 MS-BOX-PHD滤波

假设在k－1时刻的后验PHD由一组服从均匀分布的箱粒子集描述为：

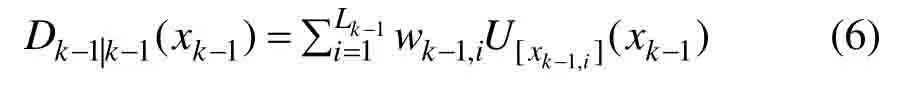
式中：[xk－1,i]为箱粒子支撑集；Lk－1为k－1时刻箱粒子的个数。

3.1 MS-BOX-PHD滤波预测

若γk(x)表示新生目标贡献强度，βSur,k(xk)表示k－1时刻到k时刻存活下来的目标贡献强度，表示k－1时刻目标x空间分布概率密度，表示目标x由k－1时刻到k时刻的转移密度，则k时刻预测PHD可以由k时刻的预测箱粒子参数集表示为：

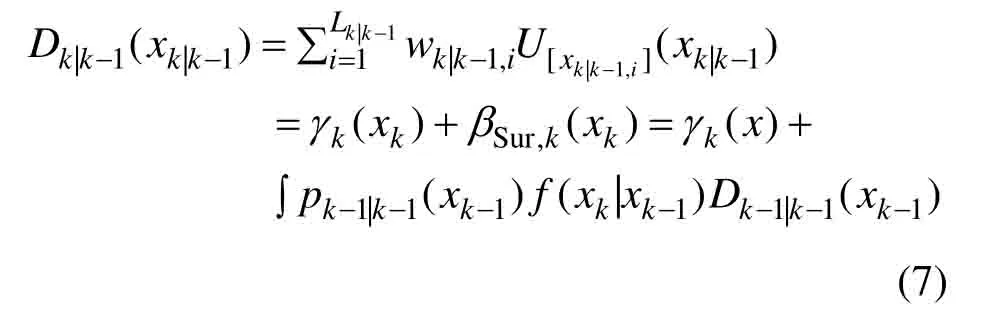
新生箱粒子根据k－1时刻量测产生[5]，在量测上服从均匀分布，为新生箱粒子集合，新生目标贡献强度γk(x)可由其表示为：

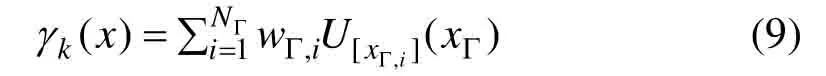
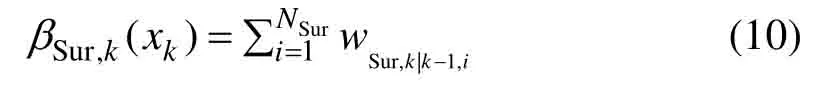
取[wk－1]为k－1 时刻的过程噪声区间，[fk－1]为k－1 时刻的状态转移函数的包含函数；pSur([⋅])表示箱粒子[⋅]的存活概率，则可由状态转移方程得到： 区1

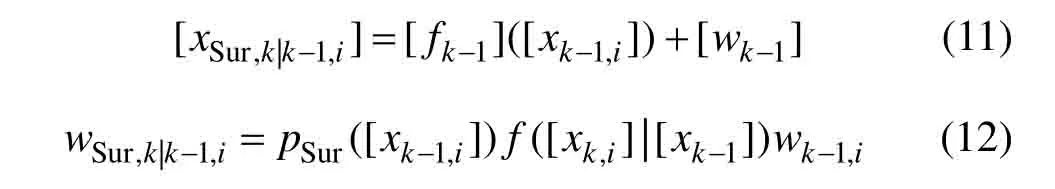
3.2 MS-BOX-PHD滤波更新

3.2.1 量测融合

量测融合分两步进行：

Step 1：输入k时刻S个传感器产生的量测集将S个传感器产生的区间量测转换到同一坐标系下，步骤如下：

输入k时刻区间量测和传感器坐标：

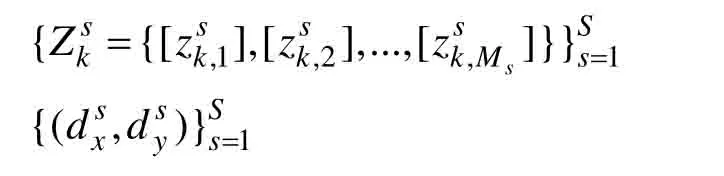
对S个传感器循环：

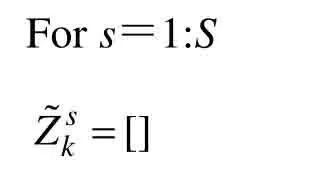
对k时刻第s个传感器产生所有量测循环：

Step 2：对S个传感器产生的量测集进行融合。若各传感器区间量测间有交集，则保留相交的区间量测的交集以及其他互不相交的区间量测值作为当前时刻区间量测集。

以两个传感器为例，对k时刻S个传感器产生的区间量测进行分析，共分为3种情况（如图1(a)、1(b)、1(c)）。

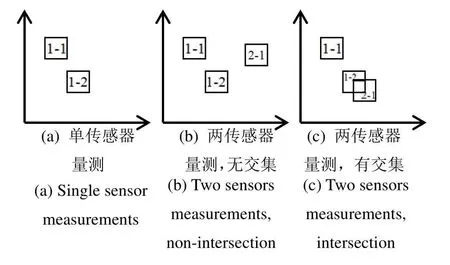
图1 传感器量测分析Fig.1 Sensor measurements analysis

假设k时刻传感器1 产生量测集经过坐标转换后记为传感器2 产生量测集经过坐标转换后为记为

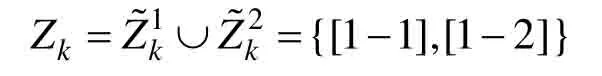
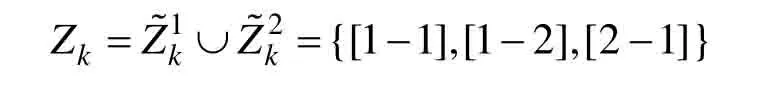
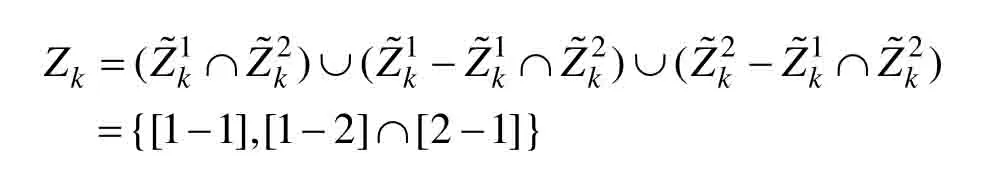
显然因为量测融合同时考虑到多个传感器的区间量测，包含目标真实信息的可能性也会更大。若其中一个传感器无法对目标进行有效检测时，其他传感器也能够对其检测并产生量测。若多个传感器同时检测到目标，则通过情形3可知，通过区间量测相交运算则能够对目标量测进行压缩，保证较小的量测区间即可包含目标信息。

通过量测融合后得到的k时刻量测融合集Zk仍然是一个随机有限集，包括真实目标产生量测和杂波。将其看作是由一个虚拟传感器产生的量测集，若第s个传感器的杂波空间分布率和杂波空间密度分别用λs和pdfs表示，则虚拟传感器的量测集中杂波概率假设密度为：

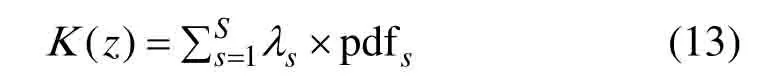
若第s个传感器的检测概率表示为pDs，则虚拟传感器的检测概率为：

3.2.2 滤波更新

输入k时刻S个传感器融合后的区间量测集Zk,对预测得到的箱粒子集进行更新。

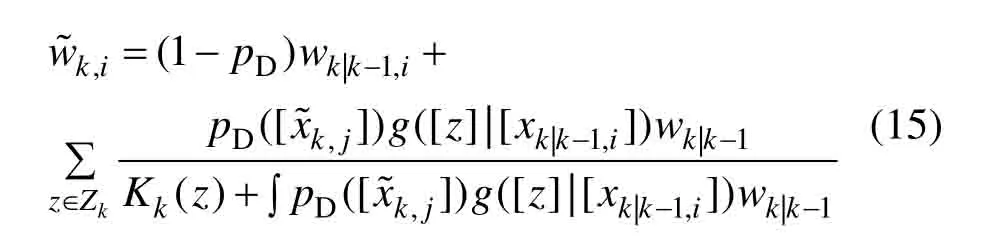
4 数值实验

实验计算机系统为Windows 10 专业版，64位操作系统。处理器为Intel(R) Core(TM) i5-6500 CPU @3.20 GHz，运行内存为8.00 GB。

实验中设置所有目标在观测区域中服从匀速直线（constant velocity,CV）运动模型：

式中：过程噪声wk为服从协方差为Q的高斯分布：

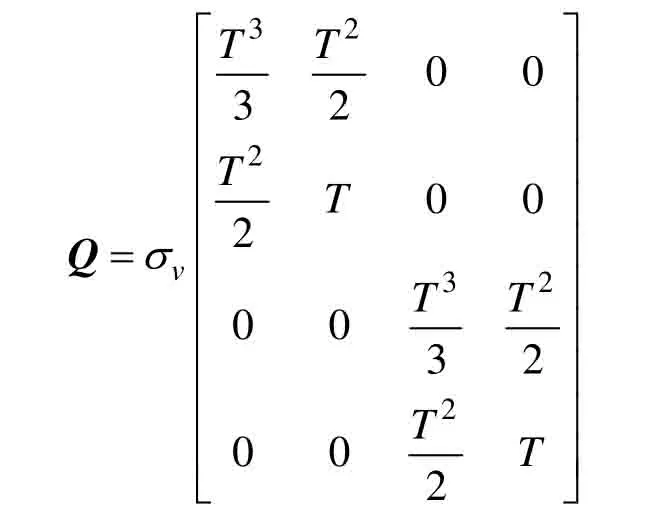
本文综合考虑位置估计误差和势估计误差，使用最优子模式分配距离[17]（optimal subpattern assignment,OSPA）来对MS-BOX-PHD滤波器的跟踪性能进行评估。对于任意的两个多目标集合X和Y，若X中包含 |m X=个状态，Y中包含 |n Y=个状态，则X和Y之间的OSPA 距离定义为：

1）当m≤n时：

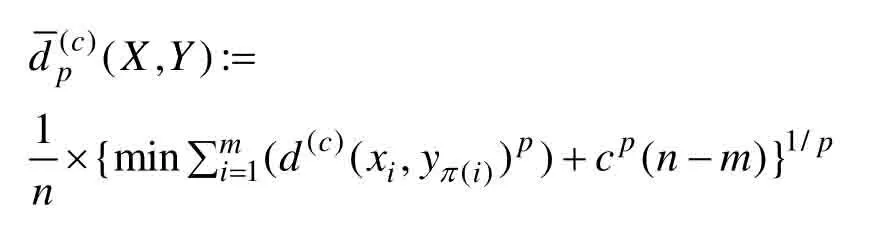
2）当m≥n时：

3）当m＝n＝0时：

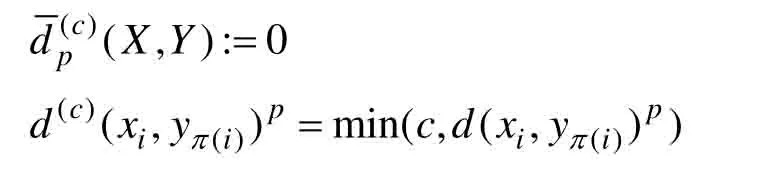
式中：c为目标个数误差惩罚参数；p为阶数，用来惩罚目标位置估计误差。本文实验中c＝100，p＝1。

4.1 场景1

设置传感器1位于坐标原点[0,0]的观测角度范围为θ1∈[0,π/2]，距离范围为r1∈[0 m,1500 m]，杂波率为λ1＝2；传感器2位于[400,0]，观测角度范围为θ2∈[π/2,π]，距离范围为r2∈[0 m,1500 m]，杂波率为λ2＝2；传感器3位于[700,600]，观测角度范围为θ2∈[－π/2,－π]，距离范围为r3∈[0 m,1500 m]，杂波率为λ3＝2。场景1 中共有10个目标随机出现和消失在所有传感器的观测区域内。试验中所有目标存活并进行状态转移的概率为pSur＝0.98。

图2为单次蒙特卡洛实验下，传感器检测概率为0.65时的目标真实位置以及传感器产生的区间量测。表1为10个目标的信息。包括目标的初始位置信息、速度信息、出生时刻和死亡时刻。

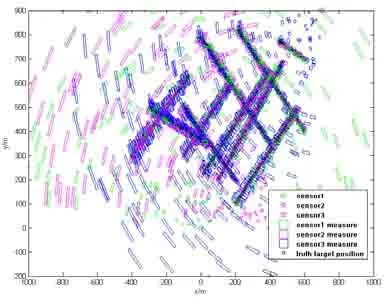
图2 目标真实位置和区间量测Fig.2 True targets location and interval measurements

表1 目标信息Table1 Information of targets

图3为单次蒙特卡洛实验下，MS-BOX-PHD滤波器在传感器检测概率都为0.65时对目标的跟踪效果图，由图3可知所提MS-BOX-PHD滤波器在检测概率较低时也能够有效地对多目标状态进行跟踪。

图4为100次蒙特卡洛实验下，MS-BOX-PHD滤波器和Single-BOX-PHD滤波器在不同检测概率下对目标的势估计图，由图 4可以看出 Single- BOX-PHD滤波在检测概率逐渐减小时，对目标个数的估计也随之减少。相对于Single-BOX-PHD滤波器，本文所提MS-BOX-PHD滤波器虽然对目标的个数估计也会受到检测概率的影响，但受影响幅度明显较小，在检测概率为0.95、0.85、0.75、0.65时都能有效地对多目标的个数进行估计。

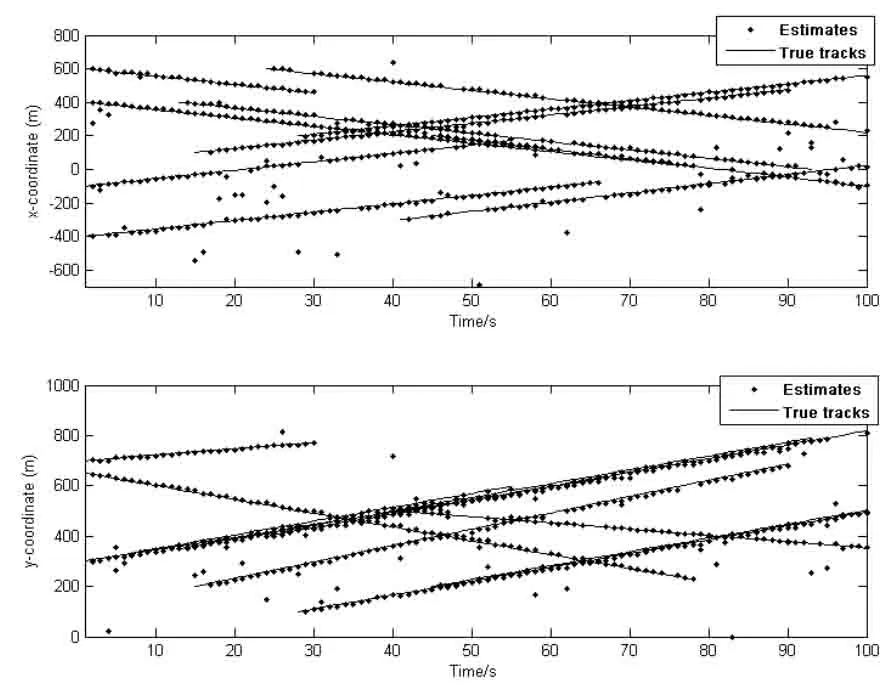
图3 在x轴和y轴目标状态估计Fig.3 Targets state estimation in x-axis and y-axis

图5为100次蒙特卡洛实验下，MS-BOX-PHD滤波和Single-BOX-PHD滤波在不同检测概率下对目标状态估计的OSPA 距离。

图5(b)为位置OSPA 距离，由图5(b)可以看出对于位置估计 MS-BOX-PHD滤波器与 Single- BOX-PHD滤波器相差不大，Single-BOX-PHD滤波器位置OSPA 距离普遍稍小是因为随着检测概率的减小，目标个数的估计会越来越少，当少估计目标个数时候，OSPA 距离只会统计估计到的目标在位置上的误差，所以随着检测概率的减小，在位置上的OSPA距离却越来越小。对于MS-BOX-PHD滤波器，能够在检测概率较小时对目标个数进行正确的估计，但在位置估计上会统计所有估计到的目标的位置OSPA距离，所以普遍稍大。且检测概率越大，对位置的估计会越精确；图5(c)为势估计OSPA 距离，由图5(c)可以看出在对目标个数估计上Single-BOX-PHD滤波器明显会受到检测概率的影响，检测概率越低，对目标个数的估计误差也越大；图5(a)为综合考虑目标位置估计和个数估计的OSPA 距离，由图5(a)可以看出MS-BOX-PHD滤波器对多目标估计的性能会受到检测概率的影响，但所受影响相对于Single-BOX-PHD滤波器受检测概率的影响要小得多，且只有在目标新生或者死亡时才会出现较大的估计误差，如第1、13、15、24、28、41、45时刻都有目标新生。说明MS-BOX-PHD滤波器在检测概率较低时，能够有效地估计多目标的状态和个数。

图4 不同检测概率下势估计（100MC）Fig.4 Cardinality estimation under different detection probabilities (100MC)

4.2 场景2

设置传感器1和传感器2的观测角度范围都为θ∈[0 rad,π rad]，距离观测范围都为r∈[37.5 m,1000 m]，杂波率为λ1＝λ2＝2；场景2 中共有2个目标，两个目标的航迹都在传感器1和传感器2的观测区域内。目标1的初始状态为[－800 m;16 m/s;100 m;7 m/s]，存活时间为1 s→100 s，目标2的初始状态为[800 m;－16 m/s;100 m;7 m/s]，存活时间为30 s→90 s。试验中所有目标存活并进行状态转移的概率为pSur＝0.98，每个目标被传感器检测到的概率都是pD＝0.65。

图6为100次蒙特卡洛实验下，MS-BOX-PHD滤波器和粒子数分别为3000个、4000个、4500个、5000个、8000个时，IM-PHD-PF 滤波器对目标势估计对比图。

由图6可以看出IM-PHD-PF 滤波器随着粒子数的增多，对势的估计也会越来越准确。但在粒子数为3000个、4000个、4500个、5000个时都没有箱粒子数为8个时MS-BOX-PHD滤波器对目标势估计准确，而在IM-PHD-PF 滤波器粒子数提高到8000个时，IM-PHD-PF 滤波器对目标的估计个数已经接近于真实目标个数。

图7为100次蒙特卡洛实验下，MS-BOX-PHD滤波器和粒子数分别为3000个、4000个、4500个、5000个、8000个时，IM-PHD-PF 滤波器对多目标状态估计的OSPA 距离。

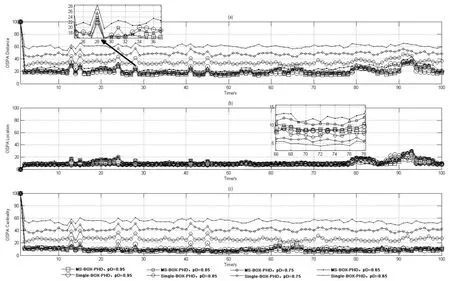
图5 不同检测概率下OSPA 距离估计（100MC）Fig.5 OSPA distance estimation under different detection probabilities (100MC)

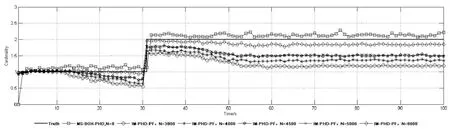
图6 MS-BOX-PHD滤波器和不同粒子数下IM-PHD-PF 滤波器对目标势估计（100MC）Fig.6 Cardinality estimation by utilizing MS-BOX-PHD filter and IM-PHD-PF filter with different number of particles,respectively (100MC)

图7 MS-BOX-PHD滤波器和不同粒子数下IM-PHD-PF 滤波器对目标状态估计的OSPA 距离（100MC）Fig.7 OSPA distance estimation by utilizing MS-BOX-PHD filter and IM-PHD-PF filter with different number of particles,respectively (100MC)

其中图7(c)为势估计OSPA 距离，图7(b)为位置估计OSPA 距离，图7(b)中，IM-PHD-PF 滤波器在位置估计OSPA 距离要比MS-BOX-PHD滤波器位置估计OSPA 距离小，因为箱粒子是一个区间，最终是使用箱粒子中心位置来对目标位置进行估计的，所以偏差要大于点粒子下IM-PHD-PF 滤波器对目标位置的估计；图7(c)则说明，粒子数越少IM-PHD-PF滤波器在对目标进行跟踪时，越容易丢失目标；图7(a)综合考虑目标的位置估计误差和势估计误差，图7(a)表明MS-BOX-PHD滤波器仅使用8个箱粒子对多目标状态估计的性能，要比IM-PHD-PF 滤波器使用3000、4000、4500、5000个粒子的情况下要稳定得多。

图7(a)中MS-BOX-PHD滤波器的OSPA 距离均值为28.4835，运行时间为14.97 s。

表2为100次蒙特卡洛实验下IM-PHD-PF 滤波器使用不同粒子数下的运行时间以及OSPA 距离均值，由表2可以看出随着粒子数目的增多，区间量测下多传感器标准PHD 粒子滤波器对多目标状态估计性能越来越好，但运行时间花费也越来越大。

综合表2以及图6和图7可知，在IM-PHD-PF滤波器使用4500个粒子时运行时间为24.37 s，OSPA 距离均值为30.14；MS-BOX-PHD滤波器使用8个箱粒子，运行时间为14.97 s，OSPA距离均值为28.4835。说明IM-PHD-PF滤波器和MS-BOX-PHD滤波器在对多目标状态估计性能相近时候，MS-BOX-PHD滤波器要比IM-PHD-PF 滤波器在计算效率上提升了38.57%。

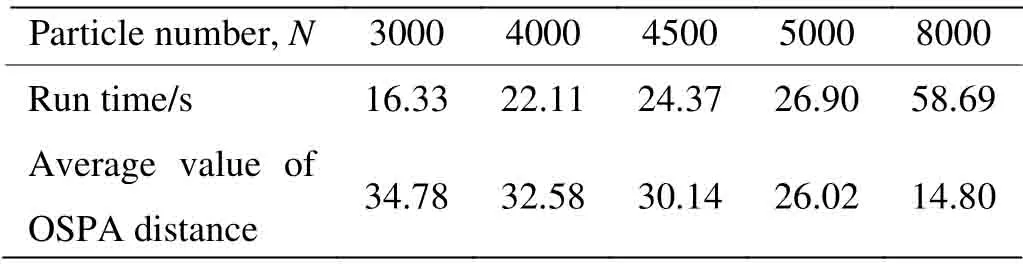
表2 IM-PHD-PF 滤波器运行时间（100MC）Table2 Time cost for IM-PHD-PF filter

5 结论

本文利用多传感器技术，结合BOX PF 以及PHD滤波器给出了MS-BOX-PHD算法的实现。并通过数值实验，验证了对于低可观测目标MS-BOX-PHD算法的优越跟踪性能，并且验证了与区间量测下多传感器标准PHD 粒子滤波器相比较，当跟踪性能接近时，MS-BOX-PHD滤波器在计算效率上提升了38.57%.