基于非参数估计的双模态红外图像差异特征频次分布构造

（中北大学 信息与通信工程学院，山西 太原 030051）

0 引言

双模态红外图像存在大气传输、成像仪响应以及目标与背景辐射强度等差异性，导致这两类图像所呈现特征的差异很大[1]。红外光强图像主要基于物体红外热辐射强度成像，该类图像的亮度信息较为明显，纹理及边缘信息较少；红外偏振度图像主要基于物体多方向偏振辐射量成像[2]，该类图像中目标的细节丰富且边缘清晰，亮度信息较少。

双模态红外图像的差异特征具有类型、幅值和频次等属性。差异特征频次属性从宏观上讲，反映了成像场景中某种差异特征分布范围的广泛性；从微观上讲，反映了特定的差异特征随着差异特征幅值变化在成像场景中分布的疏密程度。文献[3]构建了图像组中每个图像块各类型差异特征幅值对应融合算法的融合有效度分布，利用数据包络分析法（data envelopment analysis,DEA）建立差异特征与融合算法的集值映射，文献[4]研究了同类和异类差异特征幅值融合有效度的分布合成，验证了融合有效度分布合成的有效性，上述两篇文献考虑了基于类型和幅值的差异特征融合有效度分布的构建和合成，但忽视了差异特征频次属性对融合的影响，最终的结果会产生偏差。目前对于差异特征的研究只针对类型和幅值这两种属性，当差异特征频次大小发生变化时，融合算法及融合规则的选取也会随之变化。现有的这两种属性无法有效地反映出差异特征多属性对融合算法选取的影响，导致融合效果差甚至融合方法失效，所以差异特征频次的研究在图像融合中起着十分关键的作用。

因为差异特征类型、幅值分布疏密程度等因素与频次分布的函数关系是未知的，所以不同类型、不同幅值分布下无法准确得出差异特征频次服从哪些具体分布。不同差异特征幅值的分布能反映出差异特征频次的变化，差异特征幅值的概率密度分布又可以通过参数估计法得到。参数估计法中的非参数估计法针对的分布函数具体形式是未知的，样本函数与其概率密度函数服从同分布[5]，由于差异特征幅值函数形式是未知的，所以本文采用非参数概率密度估计的方法可以得到差异特征幅值样本集的概率密度分布，从而构造出差异特征频次分布。另外两种参数估计方法全参数估计和半参数估计均需要在分布函数具体形式已知的情况下进行估计[5]，故不符合本文的要求。常用的非参数概率密度估计法有KNN概率密度估计和核密度估计法。本文所提出的基于KNN概率密度估计的差异特征频次分布构造法和核密度估计相比，避免了核密度概率密度估计中核函数以及核函数带宽选择的主观性，因此能准确构造差异特征频次分布。

1 背景理论

双模态红外图像是指分别基于红外热辐射成像和红外偏振成像这两种不同的红外探测机理，并对一定的目标场景进行图像采集最后经过相应的图像信息解算所得到的两种模态的红外图像，亦即红外光强图像和红外偏振度图像。偏振光相较于传统的红外线可以将光的多个偏振形态表示出来，进而将许多人眼无法觉察到的信息显示出来，便于目标探测与识别。斯托克斯表示法[6]是常见的光波强度和偏振态的描述法，它利用4个参数I、Q、U、V可以将光的偏振状态全部表示出来，这4个参数称为斯托克斯参数，可以直接测量。设准偏振光沿Z方向传播，其平均频率为υ，并设电矢量E的x、y分量分别为Ex、Ey，如公式(1)所示：

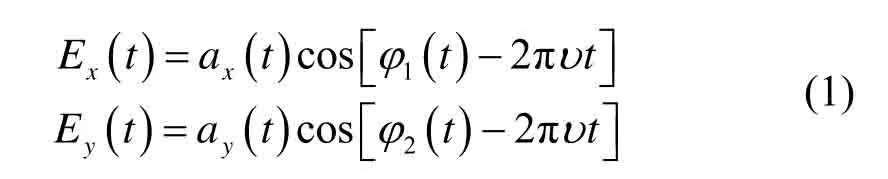
式中：ax(t)和ay(t)分别为电矢量E的振幅，化解掉公式(1)中的-2 πυ t，如公式(2)所示：

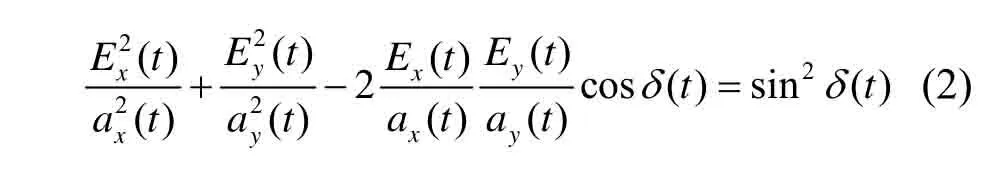
式中：δ(t) =φ2(t) -φ1(t)是Ex、Ey的相位差。

经过复杂的公式推导，由于偏振光的振幅和相位差与时间相关，可以得到推广式[7]，如公式(3)所示：

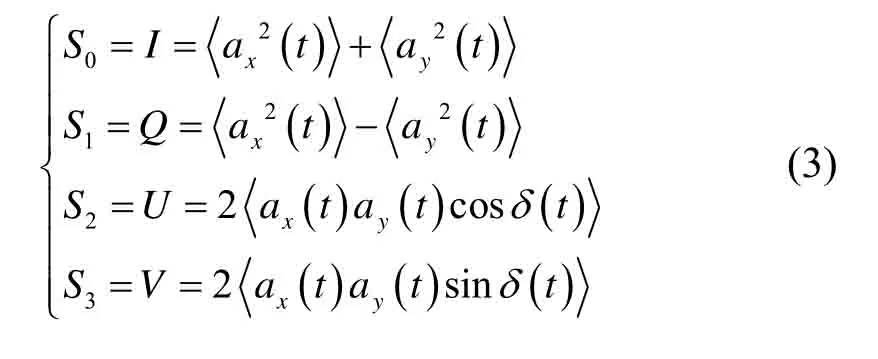
式中：I表示光的总强度；Q表示0°方向和90°方向线偏振光分量强度差值；U表示45°与135°方向线偏振光分量强度差值；而V代表右旋与左旋圆偏振光分量之差。因为在实际探测过程中，圆偏振光的分量极少且相较于仪器误差是可以忽略不计的，通常认为V＝0，因此可以直接利用I、Q、V三个独立的斯托克斯参数来准确表示一束光的偏振态，当一束光源与水平轴x夹角为α时，观测到的光强度如公式(4)所示：

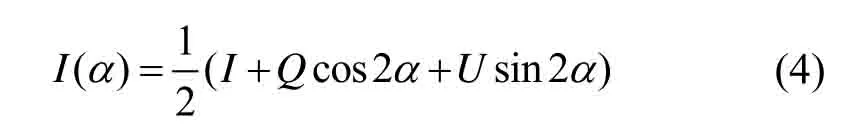
本文将0°设为参考方向并确立为初始位置，将偏振片逐步旋转到45°、90°、135°三个不同位置，并将这4个不同偏振方向的光强分量代入到公式(4)中，化解可得：

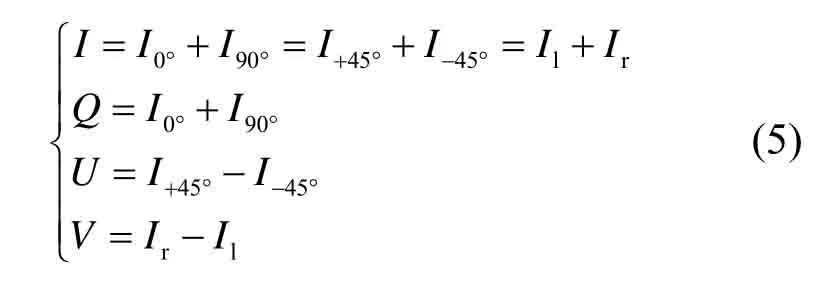
式中：I0°、I90°、I＋45°、I－45°、Ir、Il分别表示放置在光波传播路径上的理想偏振片在0°、90°、＋45°、－45°方向上的线偏振光以及左旋l和右旋r 圆偏振光。通过测出3个不同角度的光强分量可以直接计算出斯托克斯参数[8]，在图像中，参数I代表了物体的强度信息，即反映不同物体的反射比。参数Q代表了物体的材质，参数U代表了边缘和轮廓信息。偏振光的线偏振度P和偏振角θ如公式(6)所示：

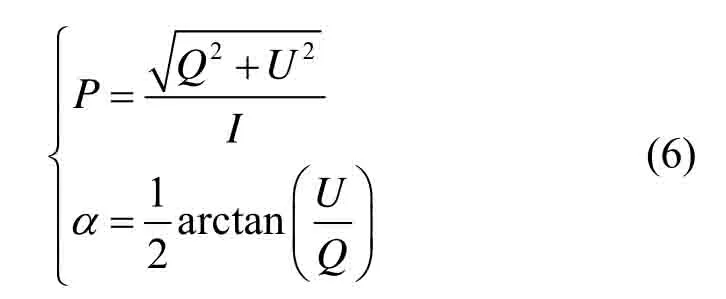
本红外偏振探测系统选取偏振度图像作为偏振成像的单模态图像，偏振度图像能够体现物体的表面边缘信息，是从自然背景中凸显出人造目标特征的方法[9]，红外偏振度图像可以很好地表示出物体材质、粗糙特性、边缘特征、轮廓信息、纹理细节，目标的对比反差度特性，但偏振片得到的辐射能量被削弱，红外辐射强度很低，所以红外偏振度图像的光强信息很弱。红外热辐射成像由于直接对目标物体进行热辐射强度成像，并未对光的多个方向的偏振态进行成像，所以得到的红外图像光强信息很高，但物体材质、纹理边缘细节、对比度信息很弱。由于红外偏振度图像和红外光强图像这两个单模态图像成像特性差异巨大，所以二者组成的双模态图像具有极大的互补性信息。通常情况下，用辐射对比度和偏振度对比度分别描述目标和背景的热辐射强度差异和偏振特性差异，辐射对比度对应在图像特征信息中表示亮度，而偏振度对比度对应在图像特征信息中表示边缘幅值强度、反差度、边缘清晰度、粗糙特性和对比度等。

差异特征幅值是指双模态红外图像特征值间强度的绝对差异度，如公式(7)所示：

式中：TI、TP、T分别表示红外偏振度图像、光强图像以及两类图像对应图像块特征值差值的强度。在不同的成像场景中，两类图像在对应的不同局部图像块中辐射对比度差异值或者偏振度对比度差异值都不同，但存在部分辐射对比度差异值或偏振度对比度差异值的大小近似相同，在图像特征信息中可表示为两类图像中亮度特征、边缘幅值强度、反差度、边缘清晰度、粗糙度和对比度等差异特征幅值大小不同，但存在大小相同的差异特征幅值（本文中将幅值大小完全相同和在一定的小范围幅值区间内的近似相同均视为相同）。

统计并研究不同大小的辐射对比度差异值和偏振度对比度差异值出现的频次能够深刻地反映出成像中热辐射强度信息和偏振度信息在双模态红外图像中分布规律，同时对于提高双模态红外图像融合质量提供了思路，上述两种对比度差异值量化到图像特征信息中则表现为统计两类图像中不同大小差异特征幅值出现的次数，即双模态红外图像中的差异特征频次。

KNN概率密度估计[10]是通过改变相同的小样本数所需的区域大小来获得估计的概率密度序列值的。设其所选定的区域内样本的个数为N，并根据总体样本集的个数确定一个参数KN，其中近邻数KN为正整数，KN的大小决定了曲线的平滑程度[11]，当KN越大，则平滑程度也越大。KNN近邻估计是在KN值固定的前提下，改变V的大小进行概率密度估计，可以更好地兼顾在高密度区域估计得到的分辨率以及低密度区域估计的连续性。

另一种概率密度估计方法为核密度估计法，核密度估计法是利用平滑的峰值函数拟合观察到的数据点，对真实的概率分布曲线进行模拟估计的一种非参数估计法[12]。但是核密度估计中涉及到内核函数的选择，常用的核密度估计函数有：高斯核函数、Epanechnikov 核函数、矩形核函数、三角形核函数、伽马核函数以及余弦核函数等[13]。同时核密度函数带宽的不同对核密度估计的影响也很大，带宽反映了核密度估计曲线的整体平滑程度，同时反映了样本在整体曲线分布中所占的比重。带宽越大，则样本点在曲线中所占比重越小，整体曲线就越平坦；反之则整体曲线就越陡峭[14]。目前对于自适应带宽的设定研究较少，通常所选的带宽是根据经验值来设定的，采用固定的经验值带宽的核密度估计产生的误差很大。所以KNN概率密度估计是一种较为客观的非参数概率密度估计方法。

2 实验

2.1 源图像采集及预处理

本实验所搭建的红外偏振探测系统由热红外成像仪、检偏器、图像采集软件和主控平台组成。所采用的长波红外热像仪DM60（型号）是由浙江大立公司生产，工作波段范围为8～14 μm，探测器焦平面的像素为384×288，视场角为16°×12°，而红外检偏器选用美国爱特蒙特光学公司生产的Zn-Se 全息线栅偏振片，有效光学口径为34 mm，消光比为100：1，透过率为90%。由于本文选用3个偏振量的成像方式对10个不同的目标场景进行偏振图像采集，并对各斯托克斯参量（I、Q、U）、偏振度、偏振角等图像信息解算，得到了相应的红外光强图像和解算后的偏振度图像分别如图1(a)、(b)所示，并分别提取所需场景目标的特征。利用PCA 融合算法得到了源图像组的融合图像，如图1(c)所示，图像大小均为256×256，并利用16×16的不重叠窗口提取每个图像块的特征值。

2.2 差异特征选取和融合有效度构造

亮度特征、边缘特征、纹理特征属于双模态红外图像主要差异特征，能够有效表征双模态红外图像的互补性特征信息。灰度均值（graymean,M）、边缘强度（edgeintensity,EI）、标准差（standard deviation,SD）、平均梯度（averagegradient,AG）分别量化表示亮度特征、边缘特征中的边缘幅值强度、反差度、边缘清晰度，纹理特征选取Tamura 纹理特征中的粗糙度（coarseness,CA）、对比度（contrast,CN）来量化表示[15]。通过表1计算得出源图像在6大主要差异特征下的幅值范围。利用融合有效度表示一定融合算法下，融合后的图像特征对融合前两类图像的有效融合程度[16]，本文选取基于距离测度的余弦相似性来表示融合有效度的大小[4]，如公式(8)所示：

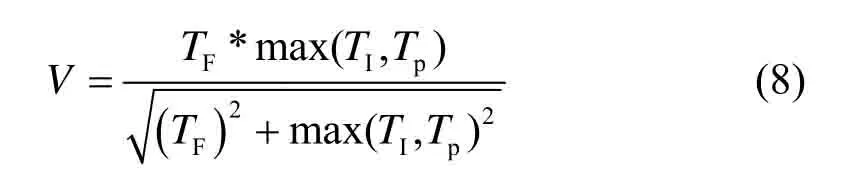
式中：TF表示融合图像的对应图像块特征值的强度。V∈(0,1]，其值越大，融合有效度越好。

差异特征属性只受到图像本身的影响，与融合算法无关。选取第4组源图像进行说明，构建差异特征的基于PCA算法的融合有效度分布图，如图2所示为差异灰度均值和差异边缘强度的融合有效度分布图。

2.3 基于KNN概率密度估计的差异特征频次分布构造

通过上述方法得到每幅源图组基于PCA算法的6种差异特征幅值散点分布图，为了更好地表示差异特征幅值的连续性，本文中将每种差异特征幅值点按从小到大划分为20组，即L＝20，幅值区间组数设为20可以更好地提升幅值区分度并减少误差[4]，便于得到差异特征幅值的不同频次值。利用累积分布函数求出每种差异特征幅值的频率分布直方图，在幅值频率分布直方图中，差异特征幅值出现频率为差异特征频次值，统计得到的每个直方图面积即为每个幅值区间内该差异特征频次的值。累积分布函数没有引入带宽等外部概念，不会丢失任何的数据信息，通过累积分布函数得到频率分布直方图是真实准确的[17]。

图1 源双模态红外图像和融合图像Fig.1 Source inf rared intensity and infrared polarization images

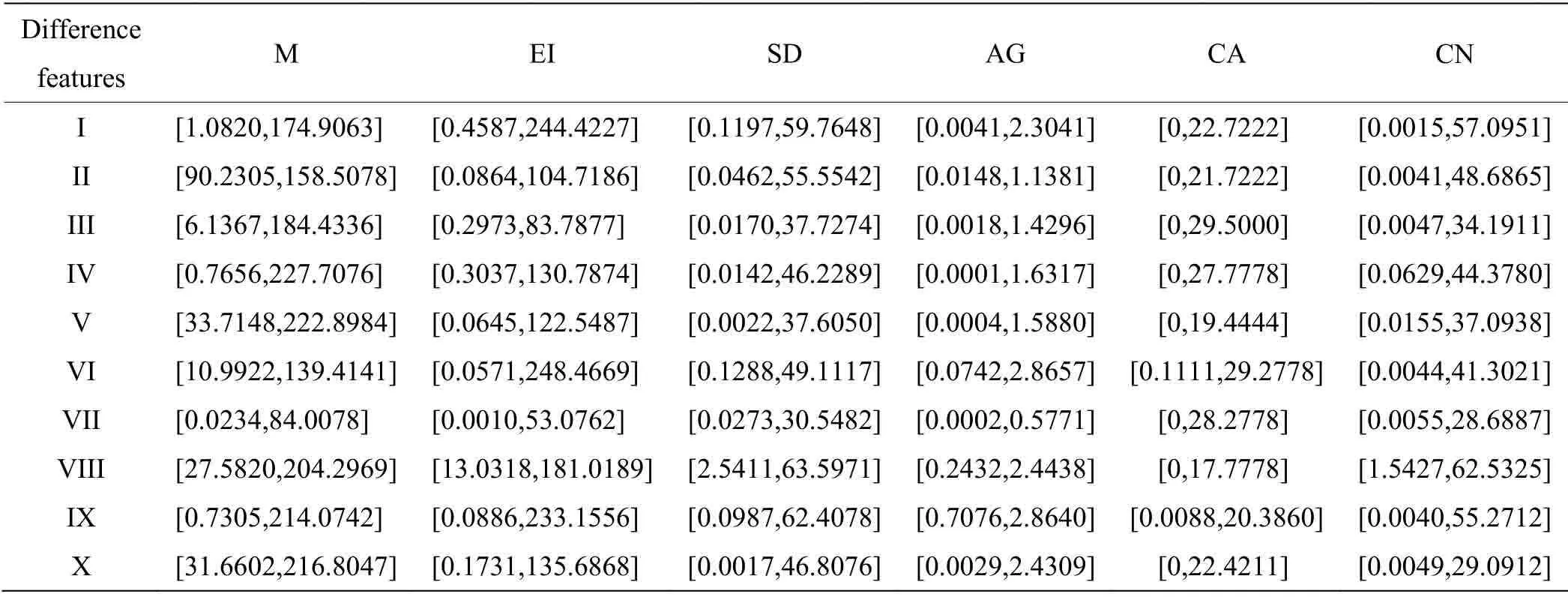
表1 源图像差异特征幅值范围Table1 Source imagesdifference features range sof amplitudes

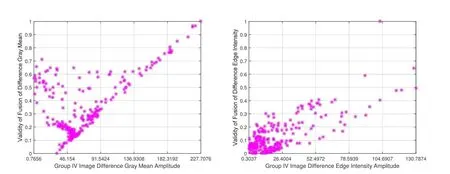
图2 融合有效度分布图Fig.2 Distribution mapsof fusion validity

本文中利用基于KNN概率密度估计的方法来构造差异特征频次分布，每幅源图组的每种差异特征幅值有256个，即N＝256，选用6种差异特征，原始样本集{Ti}所含样本个数N＝256，i＝1,2,…,N。原始样本集里所含样本个数太少不足以满足非参数概率密度估计所需样本数大的要求，所以将差异特征幅值点Ti移动的步长设为xstep＝0.01，通过插值扩充了样本集。扩充后的样本集{Tj}为第a种差异特征幅值样本集，其中a＝1,2…,6，所含样本个数为为幅值差值样本集的左边界，Tjr为幅值差值样本集的右边界，且每种差异特征幅值样本集均服从同一种分布。当变量为幅值点Tj时，通过调整包含Tj区域的体积，直到区域内刚好落入KN个样本点，所以KN取值不同时V的值也会随之改变，这些样本被称为幅值样本点Tj的KN个最近邻。

本文的幅值样本点属于一维数据，样本点相当于分布在一条线上，样本集{Tj}中任取样本jmT，V的值等于幅值样本点Tjm到它的第KN近邻距离TKN(m)的两倍，其中选用欧式距离衡量Tjm与TKN(m)间的距离大小[9]。随着步长的移动，依次求出每一个幅值点的概率密度估计值，直到Tjm＜Tjr＋xstep/2。某一特定的差异特征a的幅值点Tjm的概率密度估计值f(Tjm)如下式所示：

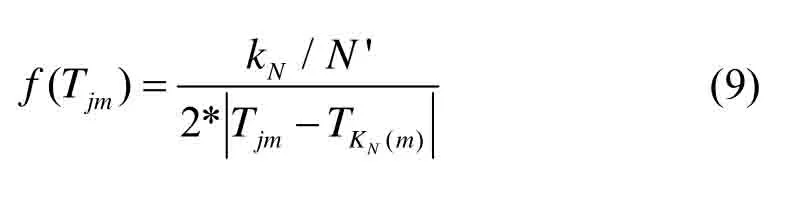
通过KNN概率密度估计得到的拟合曲线分布图中曲线的纵坐标是差异特征幅值概率密度值与横坐标对应差异特征幅值的比值，概率密度估计曲线在所有横坐标积分范围的面积恒为1。且在幅值概率密度估计曲线中，差异特征幅值密度为差异特征频次，所以通过计算概率密度估计分段曲线与横坐标子幅值区间围成的面积求出的是差异特征幅值概率密度序列值，亦即差异特征频次概率序列值。概率密度拟合曲线的表达式是未知的，通过数值积分中的复化梯形积分[18]近似可以求得分段曲线与横坐标子区间围成的面积。本文中将每组源图像的差异特征幅值区间[Tjl,Tjr]划分为n＝20个子区间，其中第k个子区间[Tjl,Tjr]也划分为n份，步长为h′＝(Trk－Tlk)/n，每个子区间包含q个差异特征幅值概率密度估计值每个子区间的节点为Tmk＝Tlk＋wh′，w＝1,2,…,n＋1，在每个差异特征幅值子区间内使用复化梯形积分，近似求得每个差异特征幅值区间差异特征频次的概率值，利用公式(10)表示：

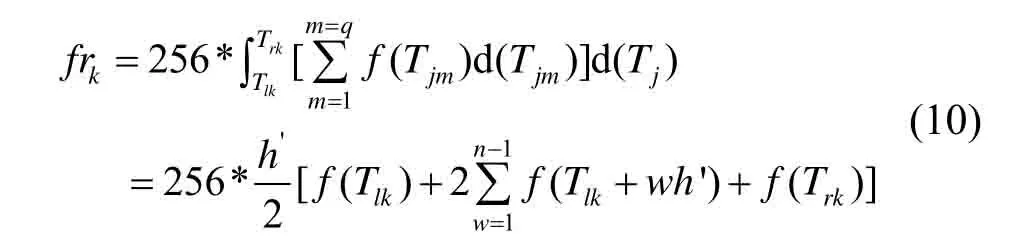
通过上式得出了每组源图像每种差异特征下基于KNN概率密度估计的差异特征频次具有统计意义的序列值{frk}，从而构造出差异特征频次分布。

3 实验结果与分析

3.1 主观分析

本文采用Matlab2014a 作为实验软件平台，实验运行环境为3 GHz Intel Core i7 PC 机，对所选取的10组双模态红外图像采用同一种融合算法进行融合（以PCA算法为例）。选用Rosenblatt 提出的积分均方误差（integral mean square error,MISE）修正固定核密度带宽参数确定最优带宽[19]的高斯核密度估计与本文方法进行对比实验，将累积分布函数统计得到的差异特征幅值的频率分布直方图、MISE 高斯核密度估计以及本文方法得到的差异特征幅值概率密度曲线进行对比，以图“IV”的6种差异特征为例，如图3所示。

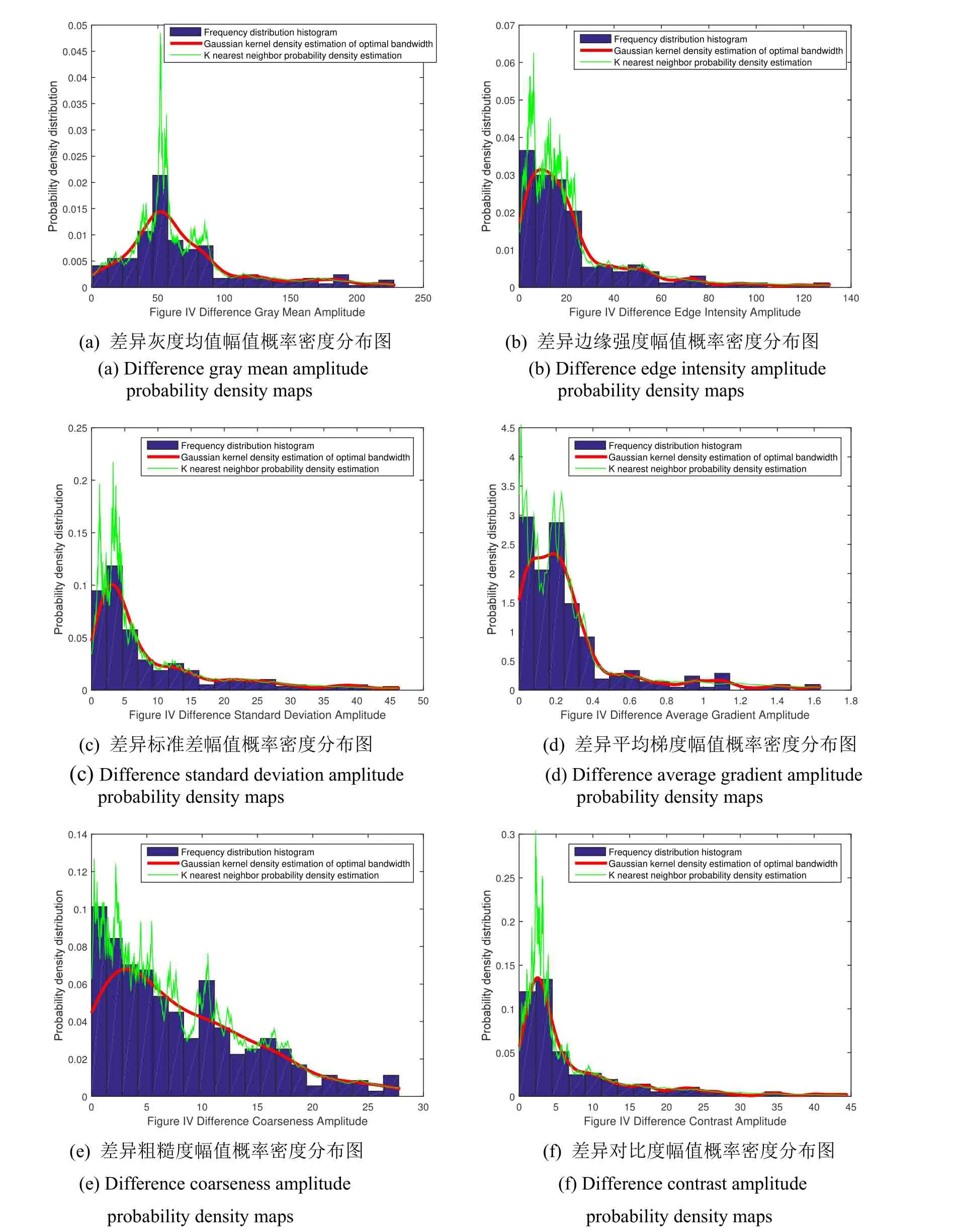
图3 差异特征幅值概率密度分布图Fig.3 Difference feature amplitude probability density maps

利用复化梯形积分构造出本文方法与最优带宽高斯核密度估计的差异特征频次分布，同时利用累积分布函数得到差异特征频次分布，每组实验源图像均分为20个幅值子区间，不同实验源图像的差异特征频次分布用虚线隔开，如图4所示。

从图3中可以看出，本文方法的差异特征幅值概率密度曲线包络与差异特征幅值的频率分布直方图更加接近（图3中以第4组双模态红外图像为例进行说明，其他源图像组实验结果与第4组源图像相同）。图4中本文方法所构造的差异特征频次分布曲线与累积分布函数得到的真实分布曲线在6种差异特征频次分布构造中重合程度很高，而基于MISE的最优带宽高斯核密度估计所构造的差异特征频次分布曲线与累积分布相比有一些偏差，尤其在差异灰度均值以及差异粗糙度频次分布构造中偏离程度较大。显然本文所提的方法构造差异特征频次分布更加准确。

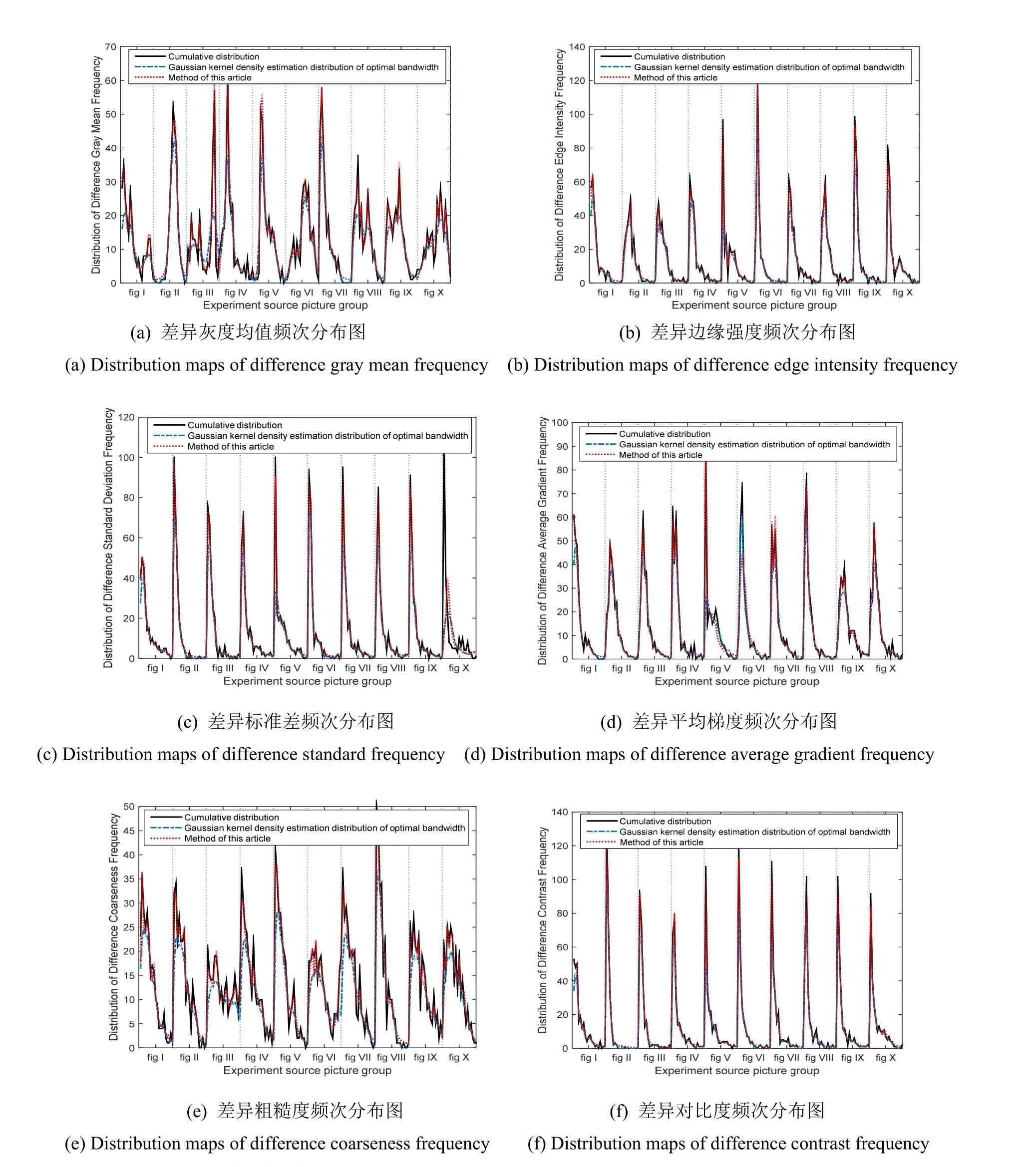
图4 差异特征频次分布图Fig.4 Distribution maps of difference feature frequency

相比较本文所提方法，MISE 最优带宽高斯核密度估计构造差异特征频次分布时产生的偏差较大，是因为如下原因：

1）选取核函数内核时，鉴于核函数在波形合成计算上的易用性，选择了高斯内核作为核密度估计函数[20]；

2）采用MISE 最小化误差函数确定核密度函数最优带宽h时，是求差异特征幅值样本集的高斯核密度估计得到的概率密度函数与原始幅值样本集的概率密度函数f(Tim)差值的均值，并作积分，进而求解最小化问题。原始差异特征幅值样本集的概率密度函数f(Tim)是未知的，所以将Sliverman 提出的经验法则法（rule-of-thumb,ROT）用于核密度函数带宽的选择[20]，即假设f(Tim)是基于高斯核方差为σ2的正态分布族。

正是上述内核函数与带宽确定造成的双重误差，导致MISE 最优带宽高斯核密度估计在差异特征频次构造中的不足，也体现了本文方法的准确性。

3.2 客观分析

分别计算最优带宽高斯核密度估计（方法1）以及本文方法（方法2）这两种频次构造方法与累积分布（真实值）之间的KL 散度[21]和Pearson 相关系数[22]，如表2和表3所示。在表2中，在6种差异特征中，本文方法相较于MISE 最优带宽高斯核密度估计的KL 散度较小，且差异灰度均值（M）和差异粗糙度（CA）二者散度差最大，差异标准差（SD）散度差小，亦即本文算法所构造的差异特征频次分布与该差异特征频次的累积分布相关性大，尤其在M和CA 中的相关性相较于最优带宽高斯核密度估计更大。

在表3中，本文方法的Pearson 相关系数比最优带宽高斯核密度估计得到的结果高，二者Pearson 相关系数的差值在M和CA 中最大，其他4类差异特征的Pearson 相关系数差值较小，本文方法与最优带宽高斯核密度估计的线性相关程度均为极强相关，但是本文算法的线性相关程度比最优带宽高斯核密度估计更高。综上，通过本文算法构造出的差异特征频次分布能够准确地反映真实的差异特征频次分布，且相较于另一种构造方法误差较小。

4 结论

本文通过构造10组双模态红外图像基于KNN概率密度估计的差异特征频次分布，并求解本文构造方法的频次分布和MISE 最优带宽高斯核密度估计的频次分布分别与累积分布的相似性测度，得出如下结论：1）非参数概率密度估计法应用于差异特征频次分布构造中具有可行性；2）从对比实验中得出本文方法对于差异特征频次分布构造的准确性优于MISE 最优带宽高斯核密度估计；3）为下一步研究基于双模态红外图像差异特征多属性的融合有效度分布合成奠定基础。

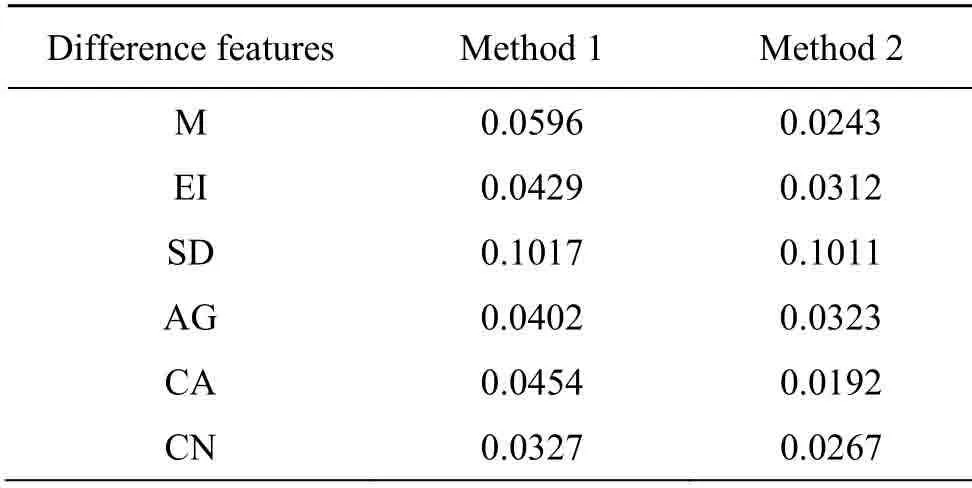
表2 不同频次构造方法与真实值的KL 散度比较Table2 Comparison of KL divergence between different frequency construction methods and real values

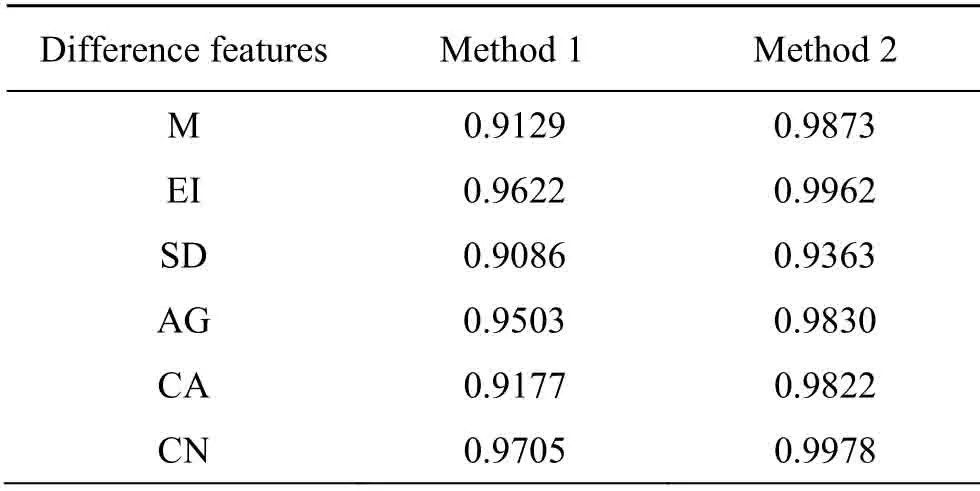
表3 不同频次构造方法与真实值的Pearson 相关系数比较Table3 Comparison of Pearson correlation coefficients between different frequency construction methods and real values