基于空-谱特征K-means的长波红外高光谱图像分类

汪凌志，雷正刚，周 浩，余春超，杨智雄，段绍丽，聂 冬

（1.昆明物理研究所，云南 昆明 650223；2.云南大学，云南 昆明 650500）

0 引言

高光谱图像是成像光谱仪通过数十至数百个窄波段电磁波对目标区域覆盖获得的数据立方体，高光谱图像同时具有空间和光谱信息，如图1所示[1]，其中坐标系XY中的像素点称为空间像素点，空间像素点在Z轴上的值称为光谱信息，Z轴上的值是该空间像素点的所有波段上的值。如今高光谱图像分类[1-3]已被广泛运用于各行业[3-5]，分类的准确率越来越重要。高光谱图像中蕴含丰富的空间和光谱信息，容易产生Hughes 现象，常用的分类方法空间利用率低等因素已成为高光谱分类的难点。

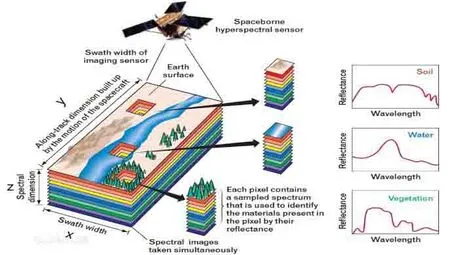
图1 高光谱图像Fig.1 HSI data

高光谱图像分类方法有很多，统计学方法因其简单、易实现、有效等原因已成为高光谱分类领域最有效、最简单的方法之一。在高光谱分类领域常用的统计学方法有光谱角度匹配算法[6]，光谱编码算法[7]，最大似然分类法[8]，K-means算法[9]等等，上述方法各有各优势。K-means 聚类因其简单、高效、易实现的特点，在各行各业已出现了各种变体，得到了广泛的运用。在高光谱的K-means 分类中一般将波段信息看成分类特征，容易造成数据冗余，导致分类困难。由此需要降低数据维度，鉴于波段选择[10]等方法需要专业知识，且容易陷入局部最优。Modha 等人[10-11]提出的特征加权K-means算法，在高光谱图像中对每个波段加上不同的特征权重，并没有有效地缓解数据冗余，除非部分波段置0，则类似于波段选择。李玉等人[12]提出的熵加权K-means算法提高了高光谱的分类准确率但还可以进一步考虑空间信息或者波段间的相关性。黄鸿等人[13]提出的加权空-谱与最近邻分类器相结合的高光谱图像分类方法，综合了空间和光谱的特征但计算较复杂，且为监督分类，通用性较差。关于长波红外的高光谱图像分类文献还相对较少，暂未发现有基于长波红外的高光谱图像的K-means 分类文献。

充分分析了长波红外高光谱数据的特点之后，提出了空-谱特征与K-means 相结合的聚类方法，并用于长波红外高光谱图像分类。其本质是对每一个空间像素点（图1中的XY坐标系中的点）赋予唯一的标识。首先提取待分类空间像素点的邻近区域信息，然后将光谱信息和处理后的空间信息结合再降维[14]得到分类特征，最后将分类特征引入K-means 聚类算法得到分类结果。本文先使用Pavia University 高光谱数据进行试验，对采用本文算法和仅用K-means算法得到的结果伪彩色图进行视觉上的分析，再定量地运用评价指标分析两种分类结果，然后将本文算法进一步应用到长波红外的高光谱数据中，最后将分类结果与用K-means算法在同一长波红外的高光谱数据得到的分类结果进行视觉上的对比。

1 算法原理

1.1 光谱特征分析

图2是机载反射光谱仪（ROSIS-03）在2003年采集的意大利北部Pavia University 数据。该光谱仪对0.43～0.86 μm 波长内的115个波段连续成像，其空间分辨率为1.3 m。一般使用剔除噪声等影响的12个波段后剩余的103个波段，原始图像每一个波段图像含有610×340个像素点。因此共有207400个像素点，但其中打上标记作为分类的像素点共42776个，其余像素点全部视为背景。已打标记的像素点一共含有9类物质，分别是asphalt（沥青）、meadows（草地）、gravel（碎石）、trees（树木）、painted metal sheets（喷漆金属板）、bare soil（裸土）、bitumen（柏油）、self-blocking bricks（砖）、shadows（阴影），每一类分别含有6631、18649、2099、3064、1345、5029、1330、3682、947个像素点。

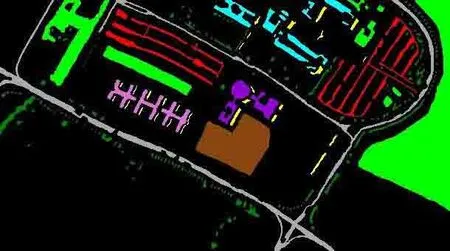
图2 帕维亚大学高光谱图片伪彩色图Fig.2 The pseudo-color picture of Pavia University

因为遥测图像的空间分辨率低，易造成一个像素点内出现多种物质，或者不同的物质由于构成材质相近造成地物的光谱曲线相似。现对Pavia University 数据重新研究分类类别，对每一类的所有空间像素点的光谱信息取平均值做图，如图3所示。

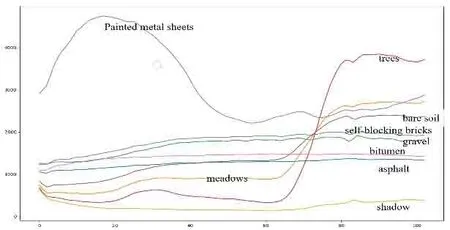
图3 9类物质的光谱测量值Fig.3 Spectral measurements of nine categories substances

图3所示，这9类物质中的柏油和沥青的光谱曲线相似，草地和裸土的光谱曲线相似，石子和砖的光谱曲线相似，其中石子和砖的光谱曲线如图4所示。由此，将Pavia University 分类的目标由原来的9类合并为6类，分别是柏油、沥青划为第一类，草地、裸土划为第二类，石子、砖划分为第三类，树木为第四类，金属板为第五类，阴影为第六类。如表1所示。

重新划分类别之后，对像素点标签进行调整之后得到划分为6类的伪彩色图像。如图5所示。

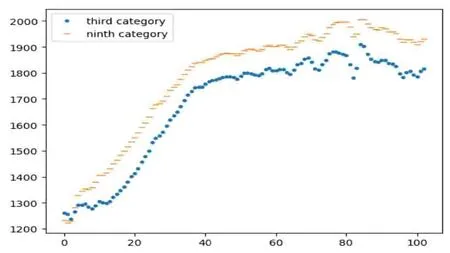
图4 第三类和第八类的光谱测量值Fig.4 Spectral measurementsfor the third and eighth categories

1.2 特征提取

假设要提取空间像素点xij的空间信息，则是提取以像素点xij为中心的a×a大小的方形区域Ω(xij)，Ω(xij)＝{xpq|p∈[i－a,i＋a],q∈[j－a,j＋a]}。在高光谱图像中，往往空间分辨率较差，例如Pavia University数据空间分辨率为1.3m。当前待分类的像素点包含1.3m 空间内的地物，如取当前点附近3×3的区域，那么就取了附近接近16m2的地物，若取当前点附近5×5的区域则是取了附近接近42m2的地物。综合来看取当前点附近3×3的区域就已经涵盖了很多种类的地物，对于连续分布的地物也能得到足够多的附近的地物信息。而取当前点附近5×5的区域会造成信息过于繁杂反而不能充分地利用空间信息，所以本文这里a取3，即提取像素点附近一共8个像素点的信息，当像素点在边缘或角落时，利用xij自身填补，如图6所示。连上xij一共9个像素点，每个像素点都是一个矢量，然后将这9个像素点整合成一个矢量，这个矢量则称为空间特征。

表1 每一类的待分类数Table1 Number of categories

在基于K-means的高光谱图像分类中，若只用光谱信息分类，则将每一个空间像素点的所有波段信息当作分类特征，本文算法是采用空间与光谱信息相结合的特征作为分类特征。首先获得待分类点的空间特征，然后对这个矢量进行降维，再将降维之后得到的矢量直接加到光谱特征矢量之后，最后再对叠加后的矢量进行降维，得到分类特征。分类特征获取过程如图7所示。

图5 Pavia University分成6类的伪彩色图Fig.5 Pavia Uni versity dividedinto sixcategories

图6 正常位置（左）、边缘位置（中）、角落位置（右）Fig.6 Normal position(left),border position(middle)and corner position(right)

图7 分类特征获取过程Fig.7 Classification f eatureacquisiti on process

本文算法的分类特征是以光谱特征为主，空间特征为辅。所以先对空间特征进行降维处理，然后再叠加到光谱特征之后，能有效地避免空间特征干扰光谱特征作为分类特征的主体。同时将叠加后的矢量再进行降维处理，能有效地避免数据冗余，进一步提高分类准确率。

1.3 降维后保留原图像信息量的选择

假设有n维向量，使用主成分降维，理论上可以降到1～n－1维。主成分降维在高光谱图像处理中实质上是对数据的压缩并最大限度地保留原数据的信息。因此需要在Pavia University 数据立方体上做主成分降维的参数选择对分类准确率影响的分析。对Pavia University 高光谱图像利用PCA（principalcomponent analysis）降维，共取6个参数，这6个参数各保留的原数据信息量分别为0.5、0.8、0.9、0.94、0.99、0.9999。并对这6个参数所对应的降维后的数据按照6类进行分类，分类结果的伪彩色图如图8所示。

根据已打好的标签可以得到各个类别的准确率和总体准确率。如表2所示。

图8 Pavia University降维后含原图像不同量图Fig.8 Pavia Universityof different information percent

由表2可见，经主成分降维后，当保留0.8 以上的原图像信息量时，分类准确率基本一致，所以在后续实验中，为了保持准确率不受影响，将高光谱图像用主成分分析法降维至保留原数据0.9的信息量的维度作为后续分类的数据。

表2 降维后Pavia University 分类准确率Table2 Classification accuracy of Pavia University after dimensionality reduction

1.4 分类评价指标

分类结束以后需要一定的评价指标对结果进行定量的分析，分类指标大部分都跟混淆矩阵有关，混淆矩阵是由分类后得到的标签与真实的标签对比得到的，混淆矩阵示例如表3所示。在表3中，有150个样本数据，共分为3类，每一类都有50个数据。分类后的结果为：类1 有45个，类2 有51个，类3有54个，将表中右下角的3×3 数据转换成矩阵则可得到此次分类结果的混淆矩阵。本文采用的评价指标都是高光谱图像分类通用的指标，本实验中一共用了3个评价指标，分别是总体分类精度、每一类分类精度和Kappa 系数。

1）总体分类精度（overall accuracy，OA）

表示分类的结果与真实结果匹配一致的概率，公式如下：

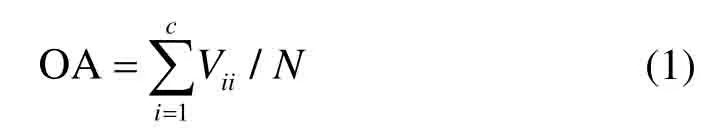
式中：c代表总的类别数；Vii代表物体属于i类被分成i类的数目，即为混淆矩阵对角线上的值；N代表样本总数。

2）每一类分类精度

表示各个类别正确分类的数目与该类数目的百分比。公式如下：

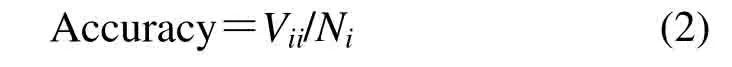
式中：Ni表示第i类物体的总数。

3）Kappa 系数

Kappa 系数是一种衡量分类精度的指标，通常结果在0～1之间，分为5组来表示不同级别的一致性：极低的一致性（0～0.20）、一般的一致性（0.21～0.40）、中等的一致性（0.41～0.60）、高度的一致性（0.61～0.80）和几乎完全一致（0.81～1）。计算公式如下：

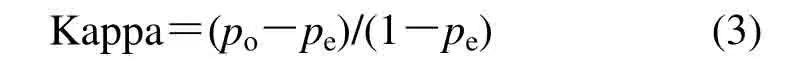
式中：po是总体分类精度；pe计算方法如下：

式中：c为样本类别总数；ai为第i类的真实个数对应混淆矩阵中的第i列；bi为被分类到第i类的数目对应中的第i行。

1.5 本文算法步骤

基于空-谱特征的K-means的分类算法具体步骤为：

输入：含有n个D维数据的高光谱图像数据X∈Rn*D，其中n为高光谱图像的总的空间像素个数，D为高光谱图像的波段数。

输出：每个空间像素点的类别

步骤1：设定a值，提取所有待分类像素点的空间特征；

步骤2：空间特征与光谱特征相结合，最终形成分类特征；

步骤3：将分类特征输入K-means算法得到每个点的类别；

步骤4：从视觉上分析分类结果或利用评价指标定量分析分类结果。

表3 混淆矩阵示范 表3The example of confusion matrix

2 实验结果及其讨论

本文所有算法的实现都基于Intel（R）Core™ i7-9750H，2.60 GHz，内存为8 GB的PC机。使用Python对高光谱数据进行分析，并验证本文算法的有效性。此实验一共使用了两组数据立方体，其一为分类数改变后的Pavia University 数据。另一为实验室采集的数据，实验室光谱仪[15]为实验室自制。

实验室光谱仪采集的高光谱图像是对物体在7.7～11.5 μm 波长内的246个波段连续成像的数据，每一个波段图像含有320×256个像素。地点为停车场，因没有打标记，所有的空间像素点都作为待分类的点，共81920个。图9为实验室光谱仪所得的可见光成像的图，该图和光谱仪的成像区域基本相同，可作为分类结果的参考。所有噪声等等都没有剔除，只能从视觉上验证本文算法的性能。

图9 实验室可见光参考数据Fig.9 Our visible reference data

对于改变分类数后的Pavia University 数据，先从视觉上分析分类结果。将利用本文算法得到的分类结果和仅使用K-means 分类得到结果作对比，分类结果的伪彩色图如图10所示。其中(a)表示的是改变类别数后的标准伪彩色图，(b)表示的是使用K-means 得到的分类结果伪彩色图，(c)表示的是采用本文算法得到的分类结果伪彩色图。(a)、(b)、(c)三张伪彩色图中每一类物质的颜色都是一样的，其中柏油、沥青为图中的道路标记为1，草地、裸土为图中标记为2的区域，石子、砖为标记为3的区域，树木为标记为4的区域，金属板和阴影分别标记为5、6，面积较大的为5，5 旁边的小块面积为6。参照(a)图可发现(b)图中序号为2的部分错分面积最大，(c)图中同样是这部分错分面积最大。但是对比(b)，(c)两图这部分可发现(c)图比(b)图错分面积小很多。同样对比(b)，(c)图右下角可以发现在序号为1的道路上（水泥、沥青）有些序号为3的部分（石子和砖），但是(c)图明显比(b)图少。也可以从3 幅图中看出，组成部分相近的，且地理位置相近的物质在K-means算法中比较容易出现误判，但本文算法在利用空间特征之后能明显地提高准确率。观察(b)，(c)图然后对比(a)图。可以发现采用本文算法的(c)图比仅用K-means 分类得到的(b)图更接近(a)图。

图10 Pavia University 分类结果图Fig.10 Classification results of Pavia University

为了定量地分析改变类别数后的Pavia University高光谱图像分类结果，计算出了本文算法和仅用K-mean算法的总体分类精度、每一类分类精度和Kappa 系数。表4呈现了两种算法的每一类的分类准确率、总体分类准确率、Kappa 系数。

如表4所示，K-means算法对第二类草地、裸土和第五类金属板的分类效果都不太好。而其他类准确率都到了80%以上。而本文算法除了第二类的准确率只有80.99%外其余都达到了90%。对比可见对第二类和第五类的本文算法较K-means算法分别提高了15%、10%，因为第二类草地、裸土和第五类金属板都是连续分布的物质，本文算法因为用了空间特征所以有效地修正了部分误分类，同时可以看到本文算法第二类中较K-means算法少了很多单独的误分类点。总体来说除了第三类和第六类，其余每一类分类效果都得到提升，而第三类和第六类在用K-means 分类时效果就达到了89%和99%的准确率，本身分类效果就很好，采用本文算法也达到了同样的准确率。仅用K-means算法的分类结果的Kappa 系数为0.69，本文算法的Kappa 系数达到了0.80。虽然都是同一级别，但整体上提高了不少。本文算法基本上每一类都较K-means算法有所提升：一是因为本文算法采用了降维，一定程度上缓解了高光谱数据的冗余；二是因为大部分地物都是空间连续分布，加入空间特征能提高分类准确率。虽然对于高光谱图像分类来说，这两种分类方法的准确度都不够高，但本文算法仍然较K-means算法提高了很多。

对于实验室自采的长波红外数据立方体的分类结果，如图11所示，(a)代表的是对采集来的数据立方体直接运用K-means算法得到的分类结果伪彩色图，(b)代表的是采用本文算法得到的分类结果伪彩色图，(c)代表的可见光图片。

从视觉上分析3 张图，只用K-means算法的分类效果较差，单独看(a)图几乎无法得到有效的信息，比如车上的玻璃没有识别出完整的形状，而且被分成了好几类，不看(c)图就无法知道是车玻璃。分类结果稍好的就是道路和水泥地，但也有大面积的误判，同时也将树和道路分成同一类物质。在本文的算法中，可以看到车的玻璃基本完全识别出来了，车的轮廓也较为清晰。同时道路和水泥地也完全分开，道路中的井盖都判断出来了，整体上也没有太大面积的误判。物体的外形轮廓也要比直接用K-means的算法分得好。但是两种算法都存在一定的误分类，有些构成相似的种类还是很难区分开。而且程序上仅用K-means算法的运行时间是本文算法的运行时间的3 倍多。

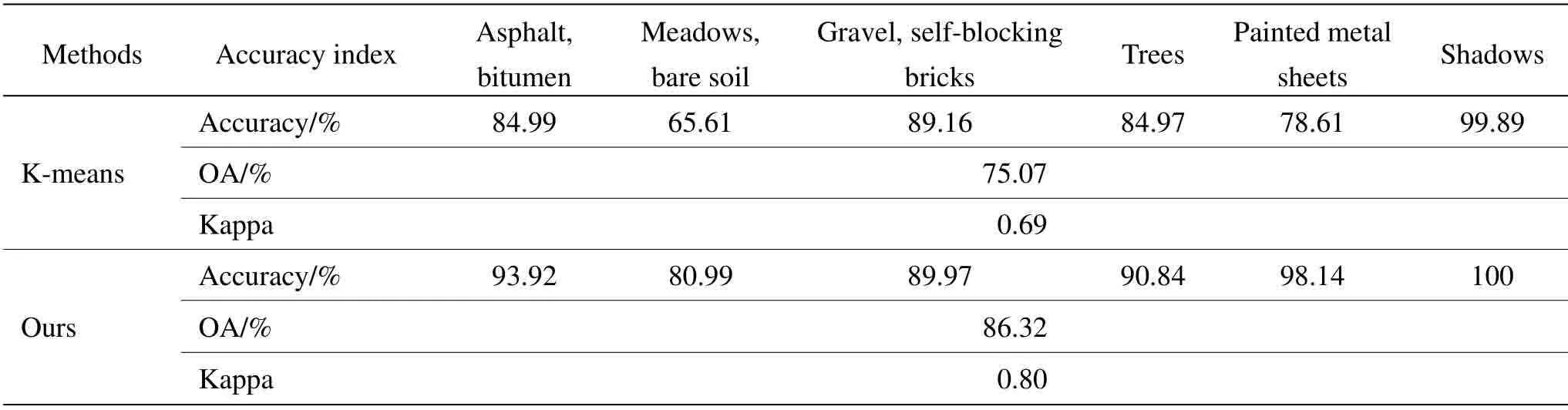
表4 分类评价指标表Table4 Classification evaluation index table

图11 实验室图片分类情况Fig.11 Classification of our data

3 结论

本文提出了基于光谱与空间特征相结合的K-means的高光谱图像分类方法，首先对每一个待分类点提取空间特征，然后将处理后的空间特征与光谱特征结合，降维得到分类特征，最后输入K-means算法，充分利用了K-means算法的便利性，又在一定程度上缓解了高光谱图像分类的数据冗余的问题，同时加入空间特征有效地提高了分类准确率。并且在长波红外的高光谱数据上运用了此方法，也取得了一定的效果。当然本方法也有不足之处，即没有充分地挖掘光谱特征。关于空间和光谱特征的融合方式本文也只是简单处理。同时对长波红外的高光谱数据的分析还不够充分。

在今后的研究中，会对空间和光谱特征融合方式做进一步研究，以及研究如何更好地降低信息冗余、挖掘出更多的有效特征和进一步分析长波红外的高光谱图像的特性，进而提高长波红外高光谱数据的分类准确率。