考虑预测误差折现效应的风电场柔性并网策略
李凌,卓毅鑫,崔长江,卢纯颢,李一铭,刘思夷,林湘宁
(1.广西电网有限责任公司电力调度控制中心,广西 南宁 530023;2. 强电磁工程与新技术国家重点实验室(华中科技大学),湖北 武汉 430074)
能源危机和环保需求促使风电等清洁能源在世界范围内得到广泛应用。然而,由于风能具有随机性和波动性,大规模风电并网将给电网安全稳定运行带来极大的挑战[1-3]。近年来,各国陆续出台相关政策,强制风电场必须采取措施改善并网功率的平滑性,实现柔性并网。例如,爱尔兰ESB公司明确规定在15 min内小于100 MW的风电场有功输出波动不大于装机容量的5%。虽然目前国内风电场并未做出相关限制,但是电力市场化和风电柔性并网的趋势必将普及到国内,研究如何实现风电柔性并网极为必要。
风电预测精度是决定风电柔性并网效果的关键因素,近年来关于风电功率预测的研究主要集中在短期预测和超短期预测[4]。在短期预测中:文献[5]基于对风电功率时间序列波动性多重机制的研究,提出一种基于多重离群点平滑转换自回归模型的风电功率预测方法;文献[6]基于风电功率数据特征聚类技术,提出一种使用经验正交函数法的区域风电功率统计升尺度预测方法;文献[7]引入非参数化方法,根据历史风资源状况得到风电出力的非参数条件概率预测结果,建立风电日前消纳调度模型。考虑到短期预测误差较大,在实际调度时进一步采用超短期预测方法提高预测精度,例如:文献[8-9]基于马尔可夫预测技术,采用小波变换理论剖析了风电出力的时频特性,得到了风电出力在实时阶段的波动变化特点;文献[10]针对不变的预测模型难以支撑短期风电功率预测模型的鲁棒性问题,提出按时间序列动态模式离散分类优化模型及在线匹配的思路;文献[11]提出一种基于风电功率超短期预测和混合储能系统实现平抑功率在电池和超级电容器之间有效分配的方法;文献[12]为最大程度地提高风电跟踪计划出力能力,基于超短期风电预测功率,建立了包含5个控制系数的储能系统充放电控制策略。上述研究为降低风电并网功率的波动性奠定了坚实的理论基础,但是并没有考虑风电功率的预测误差随时间的迁移特性。一般来说,对于前瞻周期内的不同时间断面,一般预测的时间点距离起始时刻越远,其预测误差越大[13];因此,应针对风电功率预测误差的时间迁移特性,对预测前瞻周期内各个处于不同预测精度的数据点进行差异化处理,建立更为精准的控制优化模型。
随着储能技术的发展,在风电场侧配置储能系统实现风电柔性并网的研究成果较为丰硕。文献[14]在充分分析风电功率幅频特性的基础上,提出一种基于小波包分解理论的超级电容器平抑风电场输出功率高频分量的方法;文献[15]引入并构建了基于蓄电池的风电经济性调度模型,验证了利用蓄电池提高风电并网规模、降低风电调度风险的可行性;文献[16-17]提出由超级电容器和氢储能装置组成混合储能系统,在秒级时间尺度上平抑风电并网功率和直流母线电压波动;文献[18-19]提出将风电功率波动在秒级和分钟级2种不同时间尺度上进行分解,并采用由超级电容器和蓄电池组成的混合储能系统分别平抑2个时间尺度上的功率波动,在分钟级时间尺度上除关注并网波动功率指标外,同样关注蓄电池寿命特性;文献[20]以上海东海风电场为例,对风电耦合制氢系统的运行模式进行经济性分析;文献[21]提出“波峰”制氢“削峰”、“波谷”氢气发电“填谷”的风氢互补发电系统。上述文献主要关注单一蓄电池或氢储能系统的工作特性,为风电场柔性并网奠定了坚实的理论基础,但是也存在局限性:①蓄电池-氢燃料电池在运行成本和储能效率等方面存在互补优势和协同效益,目前学界鲜有涉及;②前瞻周期内不同时间断面风电场运行成本的当前效益不同,在模型预测控制(model predictive control,MPC)调度时需要对未来收益进行差异化折现,这可能导致风电场调度策略改变,关于这方面的研究尚缺乏关注。
针对以上问题,本文立足于我国未来电力市场化趋势,以实现风电场经济性自调峰为主要目标,采用带位移因子和伸缩系数的t分布模拟超短期预测数据的预测误差,并充分考虑蓄电池和氢燃料电池的优势互补特点,对蓄-氢混合储能系统进行配置,提出一种对前瞻周期内不同时间断面的期望收益给予不同权重的滚动优化策略。最后,通过仿真分析对所提策略的合理性与可行性进行验证。
1 超短期预测误差分析
与正态分布相比,带位移因子和伸缩系数的t分布呈现胖尾特性,对风电功率分钟级误差具有更好的拟合效果[22]。t分布概率密度函数
(1)
式中:Γ为伽马函数;ν为t分布的形状系数。
文献[23]通过推导证明,对t分布进行适当的平移和伸缩变换,可得到tlocation-scale分布。若随机变量x满足tlocation-scale分布,则变量y=(x-μ)/σ满足形状系数为ν的t分布,其中μ为位置系数,σ为尺度系数。tlocation-scale分布概率密度函数可表示为
(2)
如果某变量x服从tlocation-scale分布,则该变量95%的置信区间为[-σtinv(0.975)+μ,σtinv(0.975)+μ],其中tinv为t分布的分位数函数。随着预测时间m的增加,tlocation-scale分布参数中σ逐渐增大,且呈现先快速增加后增势渐缓的特点,可采用σ=a+be-km对σ进行拟合,其中a、b、k均为拟合参数,σ随时间m的变化情况如图1所示。以此拟合不同时间预测误差曲线,效果如图2所示。
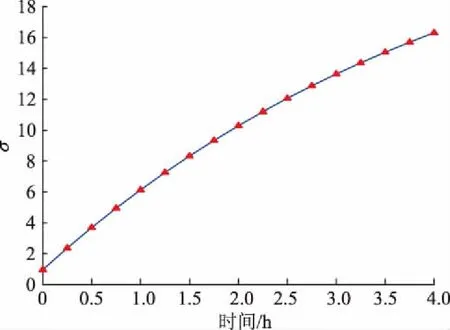
图1 t location-scale分布的σ随时间变化曲线Fig.1 σ curve in t loaction-scale distribution varying with time
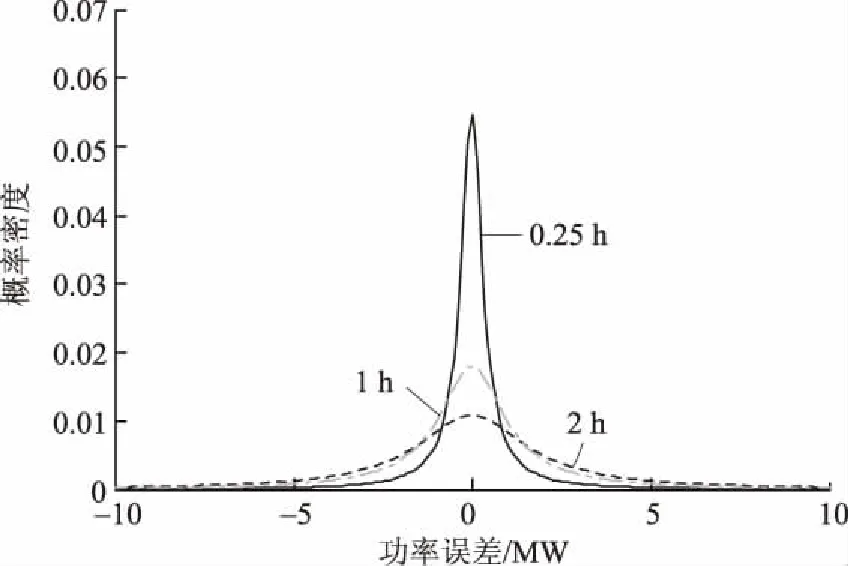
图2 0.25 h、1 h和2 h误差拟合曲线Fig.2 Fitting error curves of 0.25 h,1 h and 2 h
超短期预测误差的概率分布随时间的变化情况如图3所示。由图3可知,超短期预测误差分布随着时间的增长而变得分散,这与图2中拟合误差曲线的变化情况相印证,可见tlocation-scale分布可以较好地还原超短期预测误差变化规律。
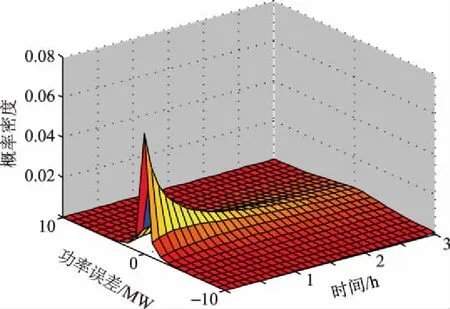
图3 3 h内的功率误差变化Fig.3 Power error change within three hours
因此,本文采用tlocation-scale分布来模拟前瞻周期内风电出力情况,力求提高对前瞻周期内风电出力的预测准确性。
2 风-蓄-氢联合系统
在现有的储能系统中,蓄电池和氢燃料电池系统备受关注。蓄电池具有灵活的调节性能,充放电效率较高,但充放电寿命损耗较为严重。氢燃料电池通过电解水制氢和氢气燃烧过程进行充放电转化,运行成本较低,但充放电过程存在严重的电量损耗。为了合理利用蓄电池与氢燃料电池的互补特性,本文将两者结合起来运用到风电场中。如图4所示,蓄电池以及氢燃料电池与风力机输出端通过母线连接,借助主变压器将风电场并网功率送至电网。功率预测系统实时预测每个前瞻周期内的风电场功率,并借助控制系统调节风电场输出功率以及蓄电池和氢燃料电池的充放电功率。
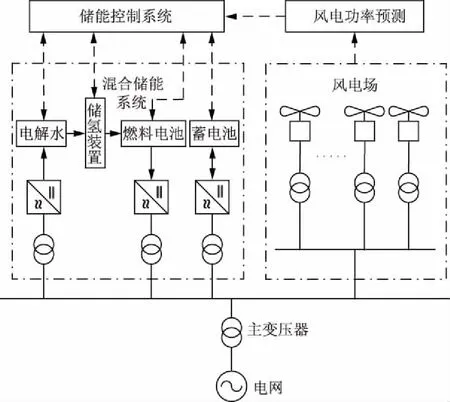
图4 风-蓄-氢联合系统Fig.4 Schematic diagram of wind-storage-hydrogen combination system
2.1 蓄电池模型
不计蓄电池的自放电过程,其充放电数学模型可表示为
EB(m)=
EB(m-1)+PBc(m)ηB-PBd(m)/ηB.
(3)
式中:EB为蓄电池的剩余能量;PBc、PBd分别为蓄电池的充电、放电功率;ηB为蓄电池的充放电效率,可达90 %。
定义蓄电池剩余能量百分比SOC为
(4)
式中EBm为蓄电池的额定容量。
2.2 氢储能系统模型
氢储能系统包括电解水装置、燃料电池和储氢装置3个部分。在风电过剩时,可借助电解水装置利用富余电能制氢,并将氢气存储于储氢装置中;在风电不足时,再将存储的氢气导入燃料电池反应产生电能,实现氢储能系统的充放电行为。对于电解水制氢过程,转化效率与输入功率之间成正相关关系,制氢装置的效率和产量随输入功率的变化关系如图5所示[24]。只有在输入功率足够大时,转化效率才较为可观,否则会因效率过低而导致运行经济性过低。
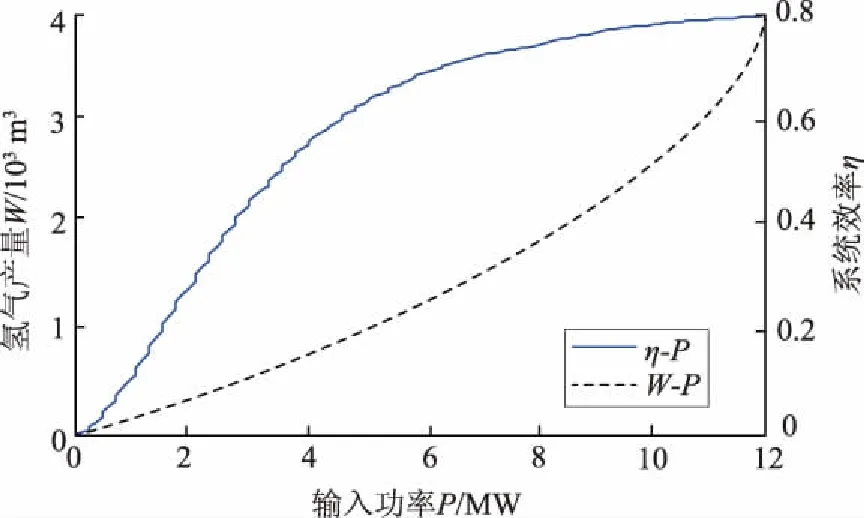
图5 氢气产量W及系统效率η曲线Fig.5 Curves of hydrogen production W and system efficiency η
电解水制氢过程储氢量WH计算公式为
WH(m)=WH(m-1)+PHc(m)ηHc.
(5)
式中:PHc为输入功率;ηHc为转化效率。
对于燃料电池,其放电效率ηHd基本可视为常数(一般为70%),在放电过程中储氢量WH可表示为
WH(m)=WH(m-1)-PHd(m)/ηHd.
(6)
式中PHd为燃料电池的输出功率。
3 风-蓄-氢联合系统滚动优化策略
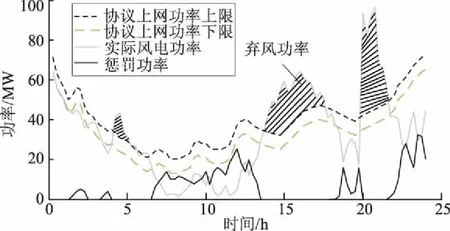
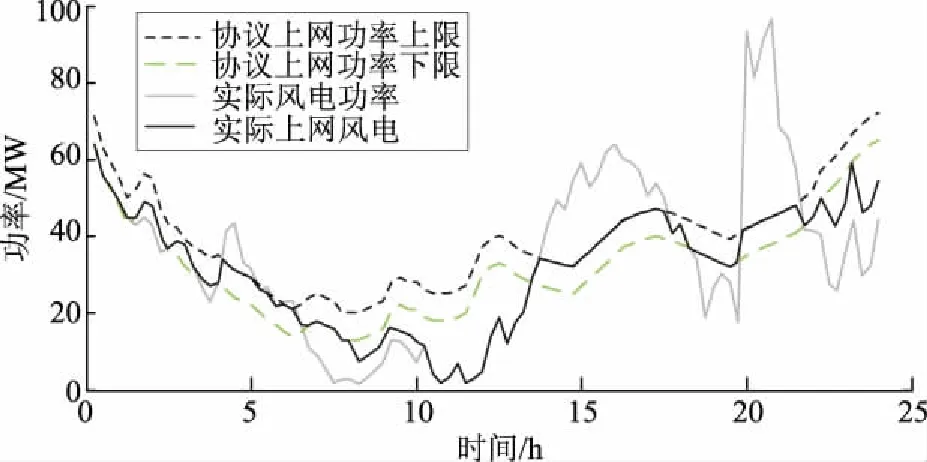
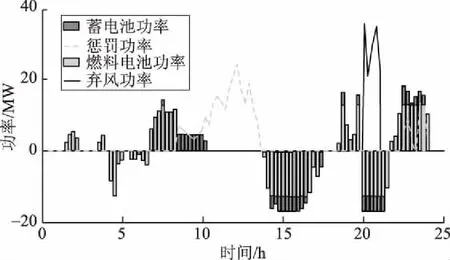
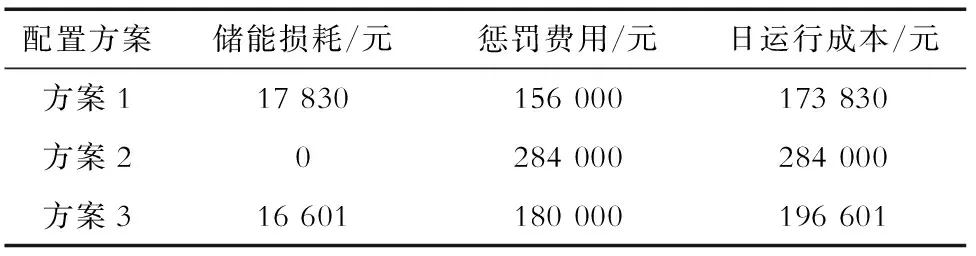
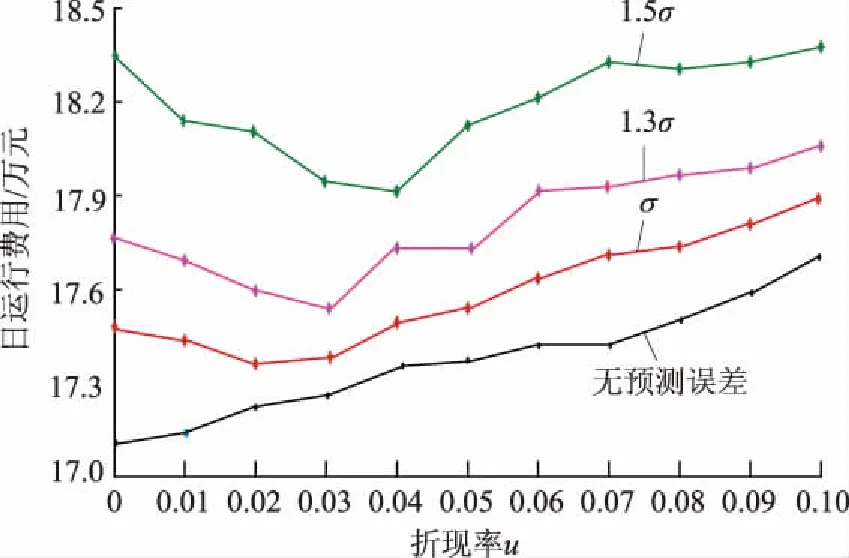
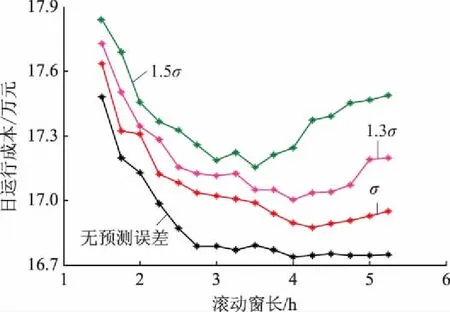
在当前的技术水平下,日前功率预测的精度尚难令人满意,协议上网功率很有可能与风电实际出力产生非常大的偏差。在电力市场环境下,电网对风电并网不仅有平滑性的要求,还会根据风电场日前预测功率,指定允许的并网风电功率波动范围[25-27]。面向电力市场的风电并网功率控制如图6所示。当风电并网功率超过预计并网功率上限即Pint>Pu-limit时,风电场将弃掉多余的风电功率;当风电并网功率小于预计并网功率下限即Pint 为此,针对基于日前功率预测的风电协议上网功率,风电场在日内调度时往往结合超短期功率预测对风-蓄-氢联合系统进行实时优化调度。为了合理计及超短期预测误差随时间推移而变大的特点, 图6 面向电力市场的风电并网功率控制Fig.6 Electricity market oriented control of wind grid-connected power 本文采用折现方法对常规目标函数进行改进,对每个时间断面目标值进行折现,提高滚动优化的准确性,降低风电运行成本。 为了合理计及风电功率超短期时变预测误差的影响,对不同时间断面风电场运行成本折现后计入综合成本。在经济学中,折现率的量化通常采用资产定价模型[27],即 Ke=Rf+βRpm. (7) 式中:Ke为权益资本成本,表示单位利益的投资成本;Rf为无风险报酬率,通常取1;β为企业风险系数,与距离预测开始的起始时间成正比;Rpm为资本溢价,通常为无风险报酬率的比例系数。 对于预测数据而言,前瞻时间越长,风险系数越大,投资成本越高。参考经济学资产定价模型,考虑未来发电不确定性的折现系数 rm=1/(1+um). (8) 式中:u为折现率;rm为前瞻周期内时间断面m的折现系数。显然,在同一时间窗内,时间越长,rm对应的值越小,此时运行状况对整体的作用就越小。 因此,以前瞻周期内风电场运行成本C最小为目标函数,即 (9) 式中:fmd为电网惩罚价格,Pmd为相应的惩罚功率;fB为蓄电池充放电单位功率运行损耗成本;M为滚动优化时段数,滚动优化的时间间隔为15 min。 a)蓄电池容量及功率约束为 SOC,min≤SOC(m)≤SOC,max. (10) 式中SOC,min、SOC,max分别为蓄电池剩余能量百分比的下限和上限,一般分别取值0.1和1.0。 此外,蓄电池具有充放电功率约束,即: 0≤PBc(m)≤PBc,max; (11) 0≤PBd(m)≤PBd,max. (12) 式中PBc,max、PBd,max分别为最大充电、放电功率。 b)氢燃料电池的约束条件包括储氢罐容量WH约束以及运行功率PH(放电为正)约束,即: 0≤WH(m)≤WH,max; (13) -PHc,max≤PH(m)≤PHd,max. (14) 式中:WH,max为储氢罐容量上限;PHc,max、PHd,max分别为氢燃料电池的最大充电、放电功率允许值。 c)风电并网功率约束为: Pr(m)=Pw(m)+PBd(m)-PBc(m)+ PHd(m)-PHc(m)-Paban(m); (15) 0.9Ppro(m)≤Pr(m)+Pmd(m)≤1.1Ppro(m). (16) 式中:Pr(m)为风电场实际并网功率;Pw(m)为风电场可发功率;Paban(m)为风电场弃风功率;Ppro(m)为风电场日前协议上网功率。 基于MPC方法,采用滚动优化的控制策略,对典型日内各个调度时刻的功率进行优化,其基本流程如图7所示,其中N为日内调度时段数,本文以15 min为时间间隔,故N=96。 图7 滚动优化流程Fig.7 Flowchart of rolling optimization 本文以某100 MW风电场为例,并配置20 MWh蓄电池和60 MWh氢储能系统,其中蓄电池最大充放电功率为5 MW,氢储能系统的最大充放电功率为12 MW。tlocation-scale分布对应参数参考文献[24],其中μ=0,ν=1.47,σ随时间的变化情况见表1。前瞻周期为2 h,滚动时间单位为15 min。 表1 σ随时间的变化Tab.1 Changes of σ varying with time 参考西班牙风电并网标准,即当风电实际上网电量与其日前发电协议出现较大偏差时,风电企业须向电网缴纳超过其上网电价数十倍的罚款,相关费用高达7.8欧元/kWh[28]。为了体现我国未来电力市场化趋势对风电场运行经济性的影响,假设风电惩罚费率为2元/kWh(为当前风电标杆电价的4倍),蓄电池损耗成本为0.8元/kWh,储氢罐容量WH2=104m3,初始时蓄电池SOC=0.5。 为深入研究风电场储能系统作用以及误差折现效果,本文设计以下3种方案进行对比分析: a)方案1:风电场配有蓄-氢储能系统,采用误差折现滚动优化。 b)方案2:风电场不配置任何储能系统,采用误差折现滚动优化。 c)方案3:风电场配有蓄-氢储能系统,但不采用误差折现滚动优化。 图 8为方案1的风电场功率分布曲线。由图8可知,虽然日内实际风电功率普遍超出了风电协议上网功率上下限,但是得益于风电场配置的蓄-氢混合储能系统的调节性能,以及误差折现滚动优化策略,优化所得的方案1中风电实际并网功率基本达到协议并网要求。在调度周期内,共有163 MWh风电功率被补偿或消纳,仅在09:30—13:00和22:45—24:00存在78 MWh风电功率缺额未被补偿。可见,方案1中的风电场实现了较好的并网效果。 图8 方案1风电场并网功率曲线Fig.8 Wind integrated power curves of scheme 1 方案1中混合储能的充放电策略(功率为正表示放电)如图9所示。由图9可知,在误差折现滚动优化策略指引下,风电超短期预测功率更为精准,蓄电池和氢燃料电池的互补特性得以充分发挥。具体而言,在风电功率缺额的07:15—09:30和18:15—20:00期间,为达到并网协议要求,风电场利用储能系统进行自调峰。由于氢储能系统无需承担额外的运行成本,运行中优先考虑氢储能系统进行放电,能量或功率受限时才采用蓄电池支撑,该段时间蓄电池释放11 MWh能量,氢燃料电池提供43 MWh能量。而在09:30—13:00,由于储能系统能量耗竭,风电场失去调节能力,不得不向电网购入64 MWh电量并支付相应惩罚费用。在风电功率较高的13:00—17:30以及20:00—22:30期间,考虑到氢储能系统运行功率较低时的低效工作特性,在富余功率较大时利用氢储能系统消纳67 MWh,而在富余功率较小时利用蓄电池消纳14 MWh富余能源。此外,受限于储能系统额定功率约束,在20:00—21:45有55 MWh风电被舍弃。可见,风电场通过蓄-氢储能系统在全时段的移峰填谷,有效减小了向电网购买的惩罚功率,从而规避了需要向电网支付高额惩罚费用的风险。 图9 方案1储能功率变化与惩罚功率Fig.9 Change of energy storage power and punish power of scheme 1 方案2风电场并网功率分布情况如图10所示。由图10可知,日内风电场出力在较长时段超出了协议并网功率上下限。较之配置了蓄-氢储能系统的方案1,方案2自调节手段十分匮乏。针对风电出力超发,风电场通过主动弃风满足并网要求。而对于风电出力短缺的场景,由于风电场内部完全缺乏功率调节手段,不得不支付因功率缺额而产生的惩罚费用。调度周期内,风电场共弃风145 MWh,产生142 MWh电量缺额。可见,缺乏储能调节手段的方案2的风电场并网功率极不理想。 图10 方案2风电场实际上网功率与惩罚功率Fig.10 Actual integrated power and punish power of wind farm of scheme 2 方案3的风电场并网功率分布情况如图11所示。由图11可知,未采用误差折现滚动优化时,风电场可能会对预测数据产生误判,导致未能有效利用蓄-氢储能系统的调节能力,在08:00—09:30导致实际上网风电出现12 MWh缺额。较之方案1,方案3尚有优化空间。 图11 方案3风电场并网功率曲线Fig.11 Integrated power of wind farm of scheme 3 进一步分析方案3中的储能系统功率分布情况。如图12所示,在滚动优化时,方案3对未来不同时段的预测数据同等对待,出现较大偏差。例如,在05:00—07:15,方案3优先使用氢-燃料电池消纳富余能源;虽然有助于降低系统运行成本,但是氢-燃料电池低效的工作状态导致能量储存量极为有限,致使在07:15—08:15的氢-燃料电池放电过程中,储存的能量被全部耗竭;在08:15—09:30,受限于额定功率,蓄电池无法独立填充风电缺额,不得不支付部分惩罚费用。可见,方案3的调度策略并不理想。 图12 方案3储能功率变化与惩罚功率Fig.12 Change of energy storage power and punish power of scheme 3 3种方案的日运行经济性见表2。由于严重缺乏调节手段,方案2日运行成本高达284 000元,在3种方案中经济性最差;方案3虽然配置了储能系统,但是由于预测误差不够精准,未能充分发挥储能系统的调节作用,日运行成本为196 601元,经济性居中;只有在配置储能系统和采用误差折现滚动优化的方案1中,日运行成本仅为173 830元,经济性最优。可见,本文所提的考虑预测误差折现效应的风电场柔性并网策略具有优越性。 表2 不同配置方案下风电场运行成本对比Tab.2 Comparisons of wind farm operation costs of different schemes 4.4.1 折现系数与误差系数的影响 为了选择最优的折现系数,针对方案1在预测误差固定的情况下改变折现系数,求取使得运行经济性最优时的折现系数。由于不同的超短期预测方法可能有不同的预测误差,进一步分析预测误差的大小对滚动优化经济性和最优折现系数的影响,结果如图13所示。 结合图13可知,当超短期预测功率不考虑预测误差时,风电场单日运行成本将随着折现率u的增大而逐渐上升,此时最优折现率u=0,采用误差折现方法并非最佳选择。而当超前预测功率以一定误差偏离实际功率时,经济成本将随着折现率u的增大呈先减小后增大趋势,但均高于忽视预测误差场景下的系统日运行成本。究其原因,前瞻周期内的功率预测误差影响了控制策略的准确性,从 图13 日运行成本随折现率的变化情况Fig.13 Changes of daily operation costs with discount rates 而使得调度成本受预测误差的影响而增大。随着折现率u不断增大,尽管功率预测误差同样存在,但对应误差较大的时间断面所占权重减小,降低了误差因素的干扰,使得控制策略更为准确。也就是说,当折现率u增大到一定程度后,未来时间断面所占权重较低,对当前决策的影响淡化,使调度策略更为注重当前运行状况,而忽略未来时间断面的潜在调峰风险,一旦出现较大功率缺额,将会导致风电场的惩罚费用增加。 考虑到不同超短期预测方法的误差存在差异,进一步研究预测误差对风电场经济成本的影响。由图13可见,随着预测误差的增加,系统整体的经济运行成本逐渐上升,对应的最优折现率u也有所减小。当预测误差为σ、1.3σ、1.5σ时,风电场最优经济成本分别为17.38万元、17.51万元、17.94万元,最优折现率分别为0.02、0.03、0.04。随着预测误差的增加,调度策略的准确性受到影响,使得调峰风险增大,经济成本也随之增加。由此可见,应增大折现率u,以减小预测误差对调度决策的影响。 4.4.2 滚动优化窗长的影响 滚动优化的效果与滚动窗长密不可分,当滚动窗长较小时,调度策略会较为短视,难以实现全局最优;当滚动窗长较大时,由于预测误差随时间增加而增大,对调度策略的准确性产生不利影响。因而在不同预测误差条件下,采用相应的最优折现率,分析滚动窗长对运行成本的影响,结果如图14所示。 由图14可知,当不考虑预测误差时,风电场运行成本随着滚动窗长的增大呈先下降后平稳趋势。究其原因,当滚动窗长较小时,储能系统不能很好地应对未来风电的变化,导致运行成本上升;随着滚动窗长增大,储能系统能较好地将未来时段风电变化纳入考量,使运行成本更为经济。随着误差水平的增大,风电场运行成本逐渐增大。当预测误差为σ、1.3σ、1.5σ时,最优窗长分别为4.25 h、4.00 h和3.50 h,原因在于预测误差越大,未来较长时段的预测误差就越大,其对调度策略的参考价值就越弱,甚至会造成误导,因而随着预测误差增大,对应最优滚动窗长将会减小。 图14 滚动窗长与日运行成本的关系Fig.14 Relationship between rolling window length and daily operation cost 为应对滚动优化前瞻周期内超短期预测误差随时间推移而逐渐增大的问题,采用带位移因子和伸缩系数的t分布对风电超短期预测误差进行拟合,并提出了一种对前瞻周期内不同时间断面的功率给予不同折现权重的滚动优化方法。主要结论如下: a)风电场侧配置蓄-氢混合储能系统有助于实现风电场柔性并网,提高风电场运行经济性,同时降低大电网运行压力。 b)考虑风电功率预测的胖尾效应,基于预测误差折现方法的滚动优化策略能够使储能的充放电控制更加准确,有助于提高风电场运行经济性。 c)增大折现率u,能够降低预测误差对风电场调度决策的影响。
3.1 目标函数
3.2 约束条件
3.3 滚动优化过程
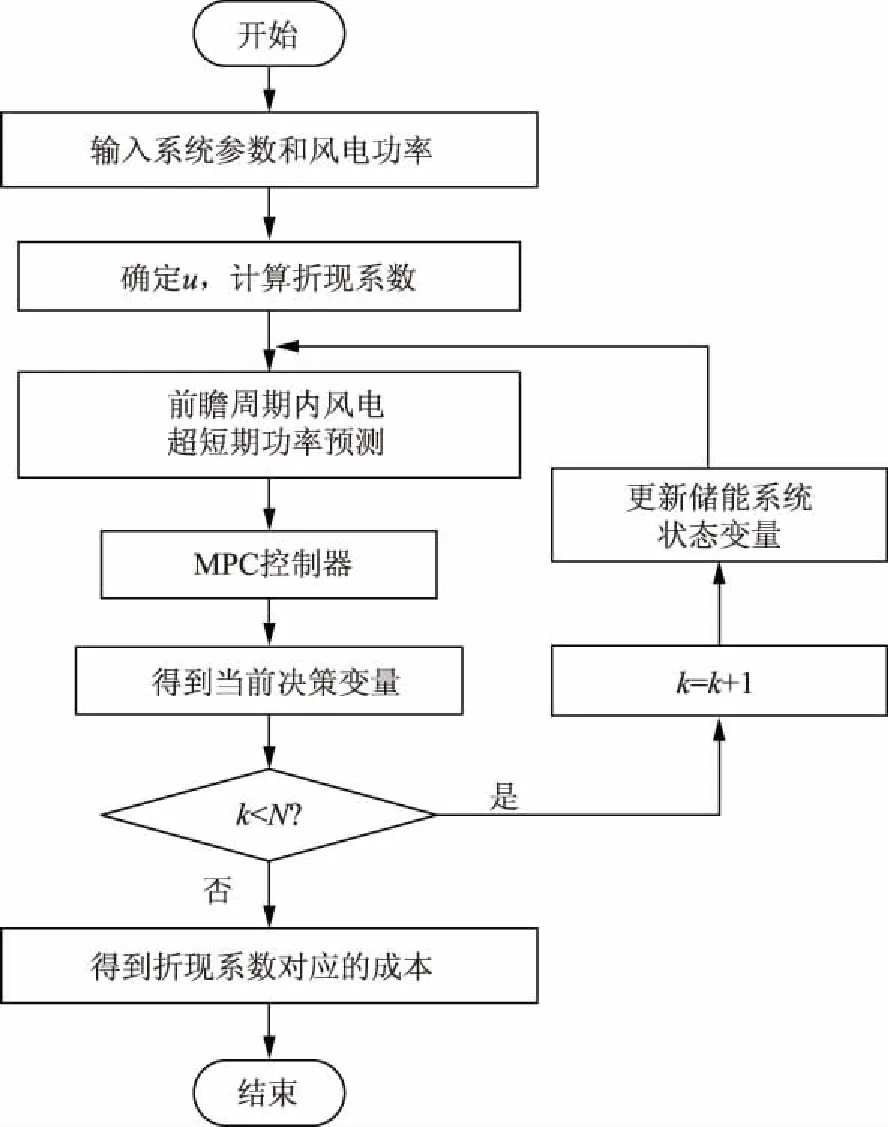
4 仿真分析
4.1 仿真算例

4.2 对比方案分析
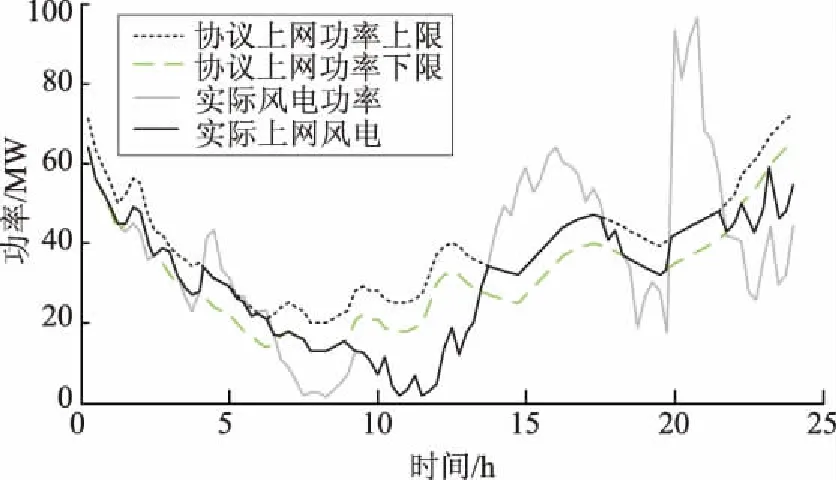
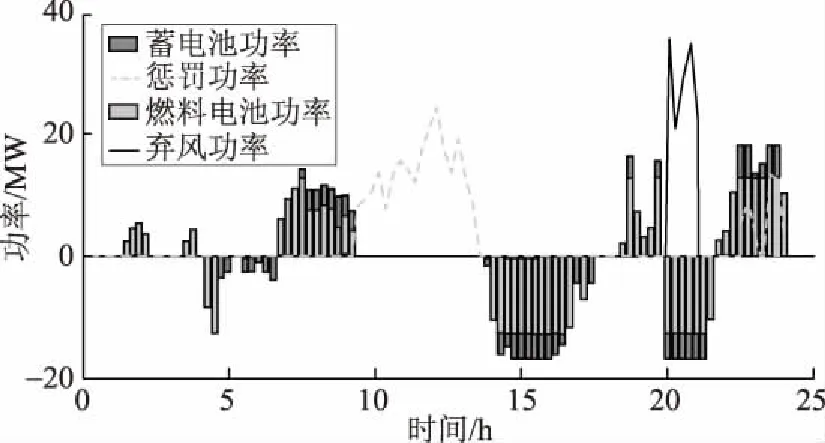
4.3 经济性分析
4.4 影响因素分析
5 结论

