解三角形中的基本问题求解策略
林 娜
(广东省中山市桂山中学 528463)
从2019年全国Ⅰ卷理科17题和全国Ⅲ卷理科18题对解三角形的考查来看,三角形中的基本方法、基本结论、基本图形和基本关系仍然是高考考查的重点,高考侧重对学生四基即基础知识、基本技能、基本思想和基本活动经验的考查.在新的问题情境下,考查学生对基础知识和基本技能的理解和掌握的情况,考查学生运用基础知识、基本技能和基本数学思想方法解决实际问题的能力,意在提升学生的数学素养,最终帮助学生建立“用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界”的能力,这才是真正地将培养学生的数学素养落在实处.下面我们通过具体例题来说明解三角形中的基本问题的解决思路和求解策略,希望对大家高三复习备考有所启发,对培养学生的数学思维有所帮助.
一、抓住基本条件和基本结论,选择合理的运算途径和方法
例题1(2019年全国Ⅰ理科17题)△ABC的内角A,B,C的对边分别为a,b,c,设(sinB-sinC)2=sin2A-sinBsinC.
(1)求A;

解(1)由已知得sin2B+sin2C-sin2A=sinBsinC,故由正弦定理得b2+c2-a2=bc.
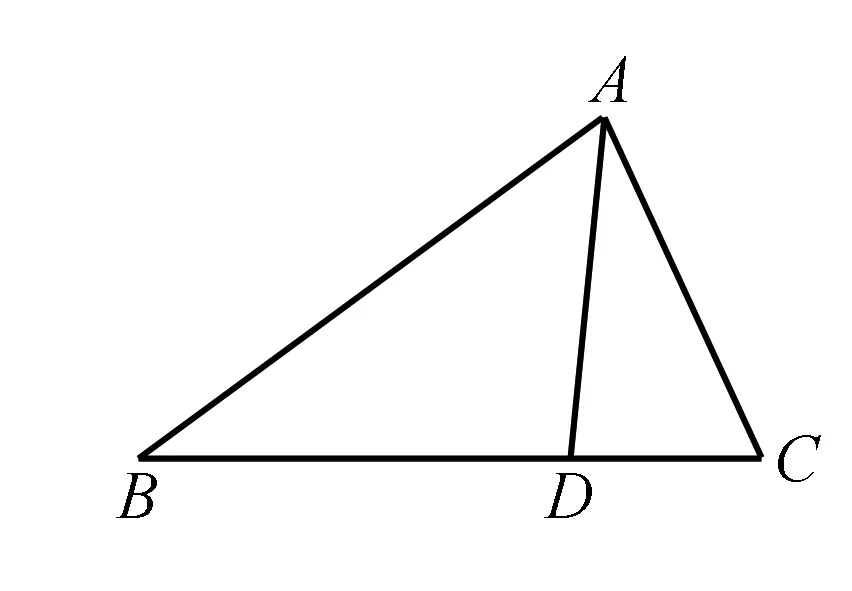
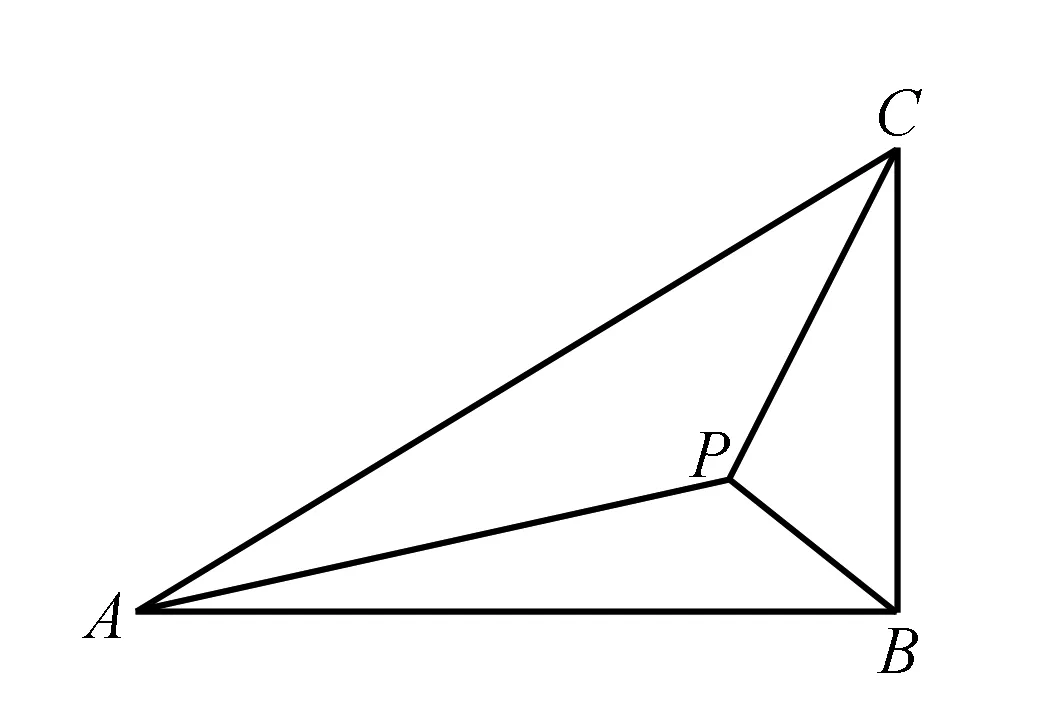
因为0° (2)思路1 (化边为角) (*)式还可以化为正弦或者也可以联立sin2C+cos2C=1来求解. 思路2 (化角为边) 思路3 (利用基本结论) 我们发现了这个题的出题思路来源于教材上同学们熟悉的射影定理,知道题目的来源为解题提供了思路,那么如何来表达呢? 解题反思思路1和思路2本质上是相同的,已知两个内角或者已知一个角和三个角的关系或者已知两组边的关系,都可以得到相似三角形,三个角确定或者三条边的比例关系确定,这是思路1和思路2的来源.在解三角形问题的时候要分析题目已知的基本条件,根据基本条件可以预想得到什么样的结果,还要看最终达到怎样的目的,最终找到运算的方向和目标.思路3来源于基本结论射影定理,也是这道题目的出题来源,如果从基本结论出发,问题马上迎刃而解. (1)求角C; (2)分析:已知角C和角B,则三角形是相似的,我们可以确定三条边的比例关系,选择哪个定理呢?如果用余弦定理将得到 解题反思这道题学生做得不好,很多学生反映很久没找到解题思路,我想归结原因,是学生没有整体分析和把握已知的基本条件,选择合理的运算路径和解题方向,迷失在两个小三角形△ABD和△ACD中.另外,由已知条件如何确定三边的比例关系,也要事先有预想,凡事预则立,不预则废,不可盲目,导致计算量加大,出错的概率增加,时间成本提高.. (2)若∠APB=150°,求tan∠PBA. 解题反思分析题目已知条件,发现无法从任何一个三角形“突破”,这个时候往往需要寻找相邻三角形边角的基本关系,利用这个基本关系,引入某个角或某条边为变量,通过这个变量建立方程. 思路1和思路2分别引入角和边为变量,建立了方程,想法本质上是一样的.但是,两种思路计算量差别很大,所以实际解题时,需要以所求为线索选择合适的方法. 变式已知平面图形ABCD为凸四边形(凸四边形即任取平面四边形一边所在的直线,其余各边均在此直线的同侧),且AB=2,BC=4,CD=5,AD=3,则四边形ABCD面积的最大值为( ). 解△ABC和△ABD中已知条件都只有两条边,无法“突破”,于是建立两者边角的联系,有公共边AC,故设AC=x,由余弦定理可得 两式平方相加得289-240cos(B+D)=49+4S2,S2=60-60cos(B+D). 解体反思通过引入△ABC和△ABD公共边AC为变量建立角B和角D的方程,利用三角形面积公式,将四边形面积表达出来,但两个角的关系比较复杂,消元难以实现,于是我们看到整体结构,将两个式子平方相加,水到渠成. (1)求B;(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围. 解(1)B=60°(过程略). 解题反思思路1和思路2是处理三角形中范围或最值问题的常规的方法,将面积表达为某个角或某条边的函数,确定函数的定义域,转化为求函数的值域问题;或者利用基本不等式来求解. 思路2重视基本图形背后的结论,即由锐角三角形知三角形中任意两边的平方和都大于第三边的平方;思路3利用动点轨迹的思想,根据已知条件,确定点C的运动轨迹,抓住基本图形直角三角形,直接“秒解”,该题是极限思想的具体运用和综合体现. 变式1 在△ABC中,已知BC=2,AB=2AC,则△ABC面积的最大值为____. 思路固定BC,由AB=2AC得到动点A的轨迹为阿波罗尼斯圆.当三角形△ABC中,BC边的高为圆的半径时,三角形的面积取最大值. 变式2 在△ABC中,已知BC=2,AB+AC=4,则△ABC面积的最大值为____. 思路固定BC,由AB+AC=4得到动点A的轨迹为椭圆,当三角形△ABC中BC边的高为椭圆的短半轴长时,三角形的面积取最大值. 变式3 在△ABC中,角A,B,C所对的边分别为a,b,c,若2a2+3b2+4c2=8,则△ABC面积的最大值为____. 解题反思变式1和变式2都是固定一条边,即三角形的两个顶点,则第三个顶点的运动轨迹分别为基本图形圆和椭圆,结合图形,答案显而易见. 变式3已知边的线性平方和为定值,可以把一条边固定(看成已知的),则问题归结为变式1和变式2类似的问题.又因为平面内到两个定点距离的平方和为定值的点的轨迹为圆,数形结合,找到取最大值的动点位置,得到关于边c的一个函数,再求函数的最大值.本题取了两次最值,这也是我们在处理双变量问题时的常见处理思路.当然这三道变式题都有很多其它解法,但其它解法相对复杂很多.如果我们能够抓住直角三角形、圆、椭圆等基本图形,数形结合,往往能够化繁为简,并且能够抓住问题的本质. 在高考中解三角形的题目主要考查考生运算能力,以及对基本结论的灵活运用能力,要尽可能地取得高分甚至满分.建议教师利用好课堂时间去引导学生思考如何选择恰当的运算路径避免繁杂的运算,如何挖掘条件中的基本条件、基本结论、基本关系、基本图形等去解决问题,化繁为简.这一基本活动经验的获得必须重视平时的思维训练,不可小觑.学生的数学素养和数学思维能力的提升最后都体现在学生解题水平的提高,这也是教师应该深思和未来努力的方向.

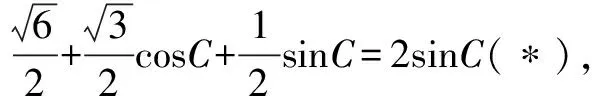
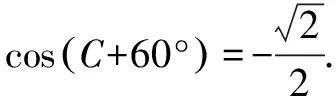
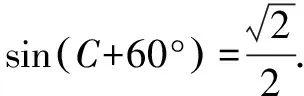
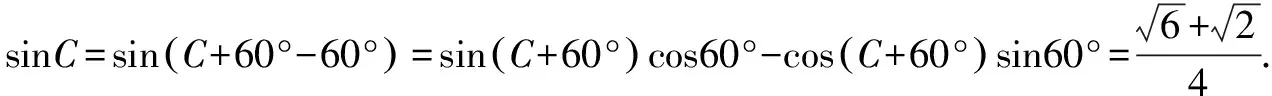


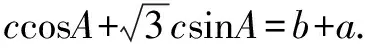
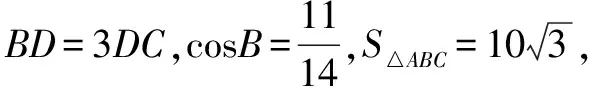




二、抓住基本边角关系,引入变量,建立方程











三、抓住基本图形,数形结合,化繁为简






四、备考建议

