三角形的内心在圆锥曲线中的应用举例
2020-05-07 03:27:34陈锦山苏艺伟
数理化解题研究 2020年13期
陈锦山 苏艺伟
(1.福建省漳州市漳浦县第四中学 363215;2.福建省龙海第一中学新校区 363100)

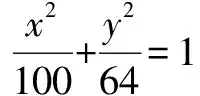
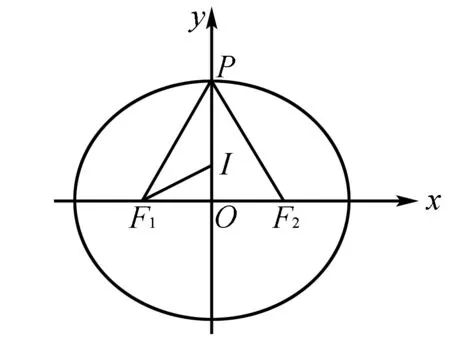
图1
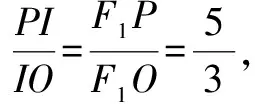
评析由于点P是椭圆上的一点,所以取特殊情况, 取点P为短轴端点,结合三角形内角平分线定理迅速求解.

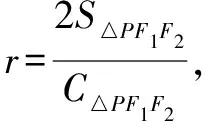
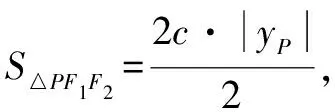
评析借助内切圆半径公式,结合椭圆性质求解,很快得到答案.

图2
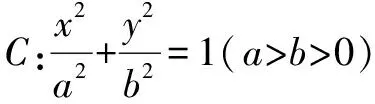
解析如图2所示,设△F1PF2的内切圆与该三角形的三边分别相切于点M,N,K.不妨设F1M=F1K=x,F2M=F2N=z,PK=PN=y.

评析借助内切圆与三角形的几何性质,结合题目条件r+c=a,得到PF1⊥PQ,这是解决本道试题的关键.
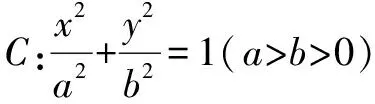
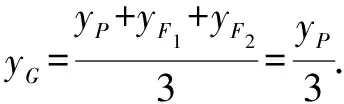
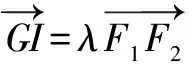
评析本题涉及到重心与内心,准确地掌握好重心和内心的相关性质是解决本道试题的关键.

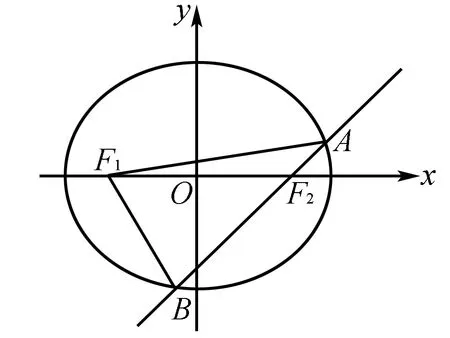
图3


评析借助内切圆半径公式,联立直线和椭圆方程求解.
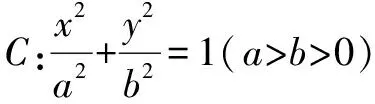
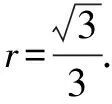
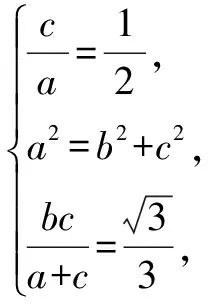
评析借助内切圆半径公式,结合椭圆中的等量关系求解.
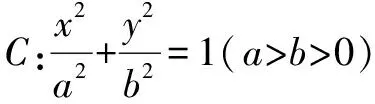

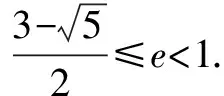
评析根据题目条件得到I是△F1MF2的内心,结合内切圆半径公式求出离心率的取值范围.
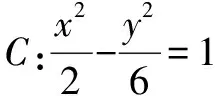
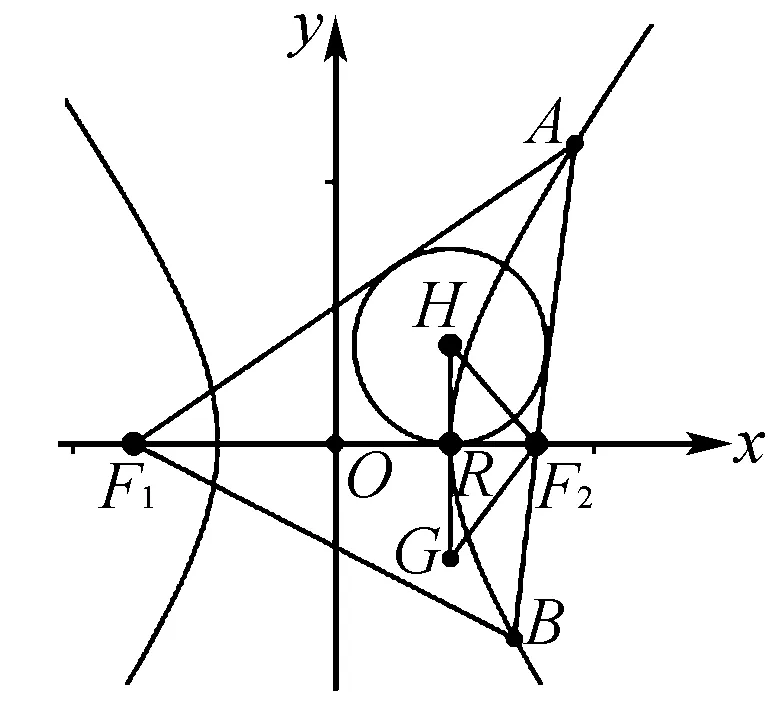
图4
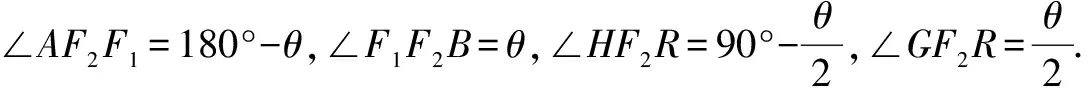
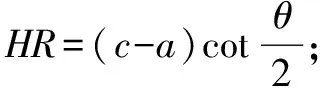
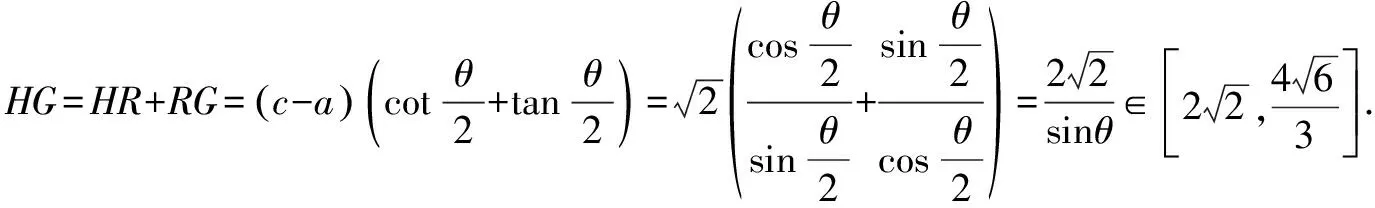
评析抓住直线AF2的倾斜角大于渐近线的倾斜角,结合内切圆的性质求解.
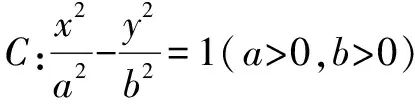

图5
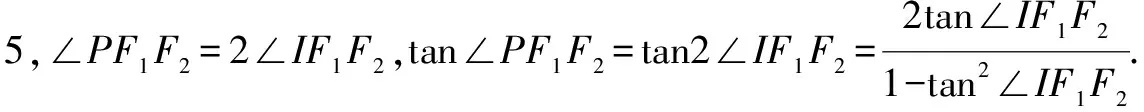

评析抓住直线PF1的斜率小于渐近线的斜率,结合内切圆的性质求解.

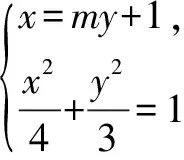
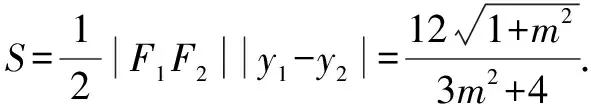


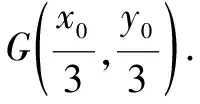

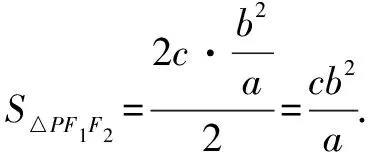
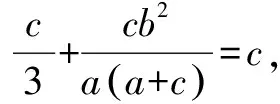


猜你喜欢
四川文理学院学报(2022年2期)2022-04-19 10:30:44
中等数学(2021年2期)2021-07-22 06:21:52
中等数学(2020年9期)2020-11-26 08:07:28
河北理科教学研究(2020年2期)2020-09-11 06:15:56
中等数学(2018年7期)2018-11-10 03:29:04
电子测试(2018年14期)2018-09-26 06:04:14
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
新高考·高二数学(2015年11期)2015-12-23 18:19:12
天津职业院校联合学报(2015年2期)2015-03-13 01:34:55
唐山学院学报(2013年3期)2013-09-27 11:48:26

