计及牵引负荷相关性的概率模型及对电力系统影响分析
罗培,谢亚文,文焱
计及牵引负荷相关性的概率模型及对电力系统影响分析
罗培1, 2,谢亚文1,文焱1
(1. 湘潭大学 信息工程学院,湖南 湘潭 411105;2. 多特蒙德工业大学能源系统,能源效率和能源经济研究所,德国 多特蒙德)
为准确描述牵引负荷的关联特性对电力系统运行产生的负面影响,引入Copula理论对牵引负荷构建具有相关性的概率分布模型,并对接入该负荷的电力系统运行进行评估。基于负荷实测数据,采用非参数核密度估计法构建累积分布函数,再根据优选指标选择最佳Copula函数,并与蒙特卡洛模拟法结合进行概率潮流计算,以实测负荷为参考,采用偏差程度、不平衡度与波动程度对所建相关性模型进行准确性评估。将计及相关性、不计相关性的模拟负荷和实测负荷依次接入IEEE-30节点系统。研究结果表明:计及相关性负荷如同实测负荷会引起电力系统较大波动,验证了所建模型的适用性和准确性,为系统安全运行提供参考价值。
牵引负荷;相关性;Copula 理论;电力系统;概率潮流

近年来高速铁路快速发展,铁路牵引负荷对电力系统的不良影响日益严峻。由于牵引负荷具有较强的随机波动性和相关特性,使得负荷行为难以准确描述[1−2]。现阶段对牵引负荷的随机波动特性研究已较深入,而对其相关特性关注却很少。所以,如何准确描述牵引负荷的相关特性并分析其对电力系统的影响是一个值得研究的问题。目前的研究侧重分析牵引负荷的随机波动性[3−4],考虑负荷间相关特性的研究国内外开展的很少[7]。杨少兵[3]采用参数识别法分段表述牵引负荷的分布模型的建模思路,方法简单但不具有通用性。王芳等[4]将牵引负荷视为恒功率源进行网压分析,模型误差较大。Trevor[5]针对牵引负荷的随机波动性,用随机过程描述负荷变化,可较真实地模拟负荷分布特征。王斌等[6]基于牵引变电所实测负序电流,通过概率统计建立的负序概率分布可以较真实的模拟实际负序电流分布情况。高锋阳等[7]建立了计及牵引负荷相关性的负荷模型,但采用参数法构建的概率模型与实际分布误差较大。如何准确建立计及牵引负荷相关性的概率模型并分析其对电力系统的影响,还有待进一步研究。Copula 理论作为研究多个随机变量间相关特性的常用数学工具,在金融和新能源领域应用广泛[8−10]。韦艳华等[8]运用 Copula技术对金融市场中存在的相关性问题展开分析,并对中国股市各板块的相关关系进行实证研究。Pagaefthymiou等[9]提出风电出力不仅具有波动性还具有相关性,使描述风电出力特征的模型更加完整。WANG等[10]为了更精准表述变量间的相关性,采用混合Copula函数构建多风电场出力联合概率模型的方法,可以得到比较可靠的潮流计算结果。目前,Copula 理论在某些应用方面已较成熟,但其在高速铁路牵引负荷领域应用较少。因此,本文提出将Copula 理论应用于高速铁路牵引负荷的相关性建模,并分析其对电力系统的影响。首先,将牵引负荷等效为两供电臂负荷的合成,通过对负荷实测数据的统计处理,采用非参数核密度估计法构建累积分布函数;然后,利用常见的5类Copula函数分别构建不同分布特性的联合概率模型,并根据优选指标选择最佳Copula 函数并生成相关性模型;最后,将牵引负荷的相关特性与蒙特卡洛模拟法(Monte Carlo Simulation Method,MCSM)结合进行概率潮流计算,在接入牵引负荷的IEEE-30节点系统上分析牵引负荷相关性对电力系统的影响,同时也验证了所提相关性模型的适用性与准确性。
1 牵引负荷相关特性描述
1.1 牵引负荷特征
目前建立的考虑随机波动性的牵引负荷模型一般需要考虑线路坡道、行车密度、限速等因素,建模难度大且不能准确反映实际概率分布特征,并不利于开展牵引负荷相关性建模及对电力系统的影响分析。为了全面可靠的描述牵引负荷特性,可把供电臂上的各种负荷等效为一个供电臂负荷,通过实测数据反映分布特征,可避免诸多因素对建模的影响。如图1所示,牵引变电所牵引负荷由AB 2个供电臂负荷组成的单相负荷,牵引负荷的功率等于两供电臂功率之和,并采用基于实测数据研究牵引负荷相关性的方法,可有效提高建模的准确性。
本文以湖南某牵引变电所AB供电臂现场测量的负荷有功数据为例进行研究。为了便于分析,首先对原始数据进行预处理:对出现零值项和个别独立数据进行了适当删减,即对无发车和低密度发车适当缩减,得到36 000组有效实测数据,在基本不影响负荷特性的情况下大大提高了分析的简便性。图2为供电臂负荷有功功率频率直方图,求得偏度值为1.388 6,说明牵引负荷有功是非对称的;对其进行-检验发现该负荷有功并不服从正态分布;另作2负荷的Q-Q分布见图3所示,图中牵引负荷有功的分布点基本集中于对角线上,说明两负荷存在较强的相关关系,这种相关性会对电力系统运行带来影响。因此,本文基于实测数据,引入 Copula 理论对牵引负荷相关性进行联合概率建模。
1.2 累积分布函数
当牵引负荷属于不规则分布函数时,用参数估计法得到的累积分布函数准确性偏低,而运用非参数核密度估计式(1)拟合得到的累积分布函数可以反映实际分布中存在的分布不对称、多峰等情况,并且该方法不需要提前做出任何参数假定,因而适用性更加广泛。

式中:h为窗宽系数;n为样本容量;K(·)为核函数。
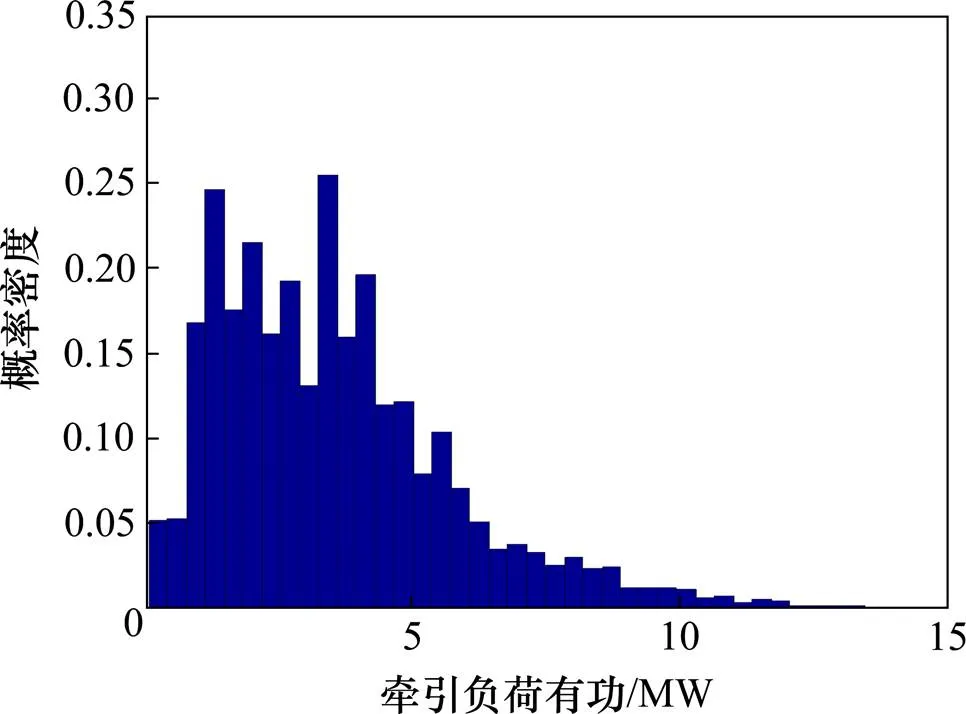
图2 牵引负荷有功功率直方图
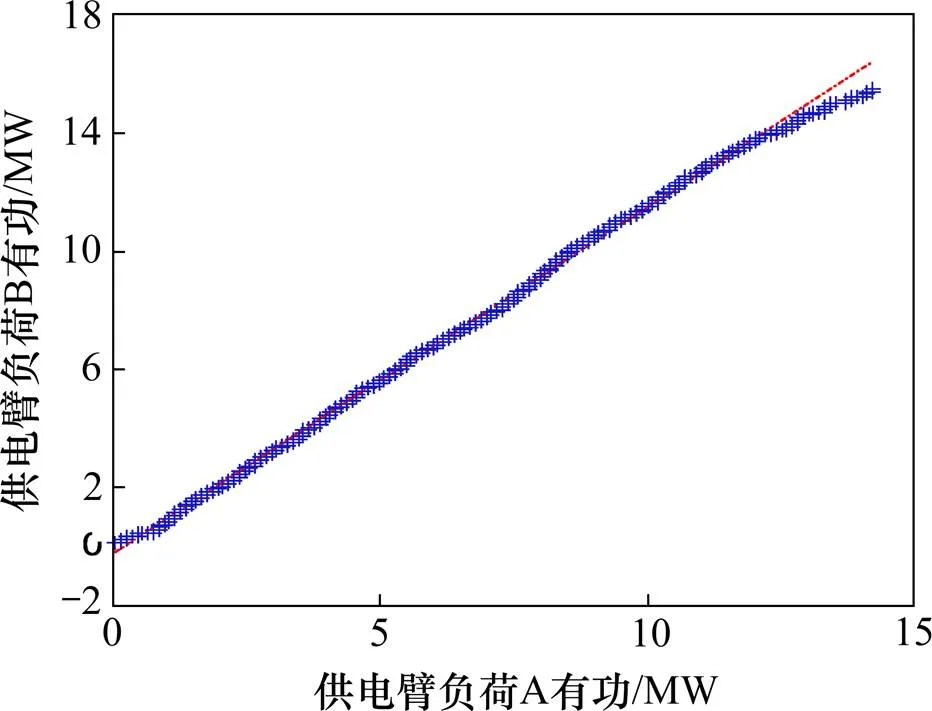
图3 两供电臂负荷有功的 Q-Q 图
采用经验累积分布函数对其进行拟合优度检验,经验累积分布函数=e()是实际分布函数的一个逼近,可用于比较拟合结果的优劣性,其逆函数=−1()可用于生成满足相关性条件的模拟负荷,计算步骤如下:

2)牵引负荷经验累积分布函数=e()与其逆函数=−1()的计算公式如下:


式中:表示只保留整数部分,小数部分四舍五入。
基于实测数据,选取高斯核作为核函数[11],根据最优宽窗的优化模型选择最优宽窗0[12],求得()后,对其积分即可得累积分布函数()。由图4可见,非参数核密度估计法得到的结果与经验累积分布函数十分接近,可见该方法是准确有效的。

图4 经验分布函数与核分布函数对比
2 基于Copula理论的牵引负荷建模
2.1 Copula函数
Copula函数被用来描述多元随机变量间的相关性,是一种可以将随机变量的联合累积分布函数与它们各自的边缘累积分布函数连接在一起的函数,通常也被称为连接函数。由Sklar定理[13]可知:若随机变量(1,2,…,X)的联合分布函数为(1,2,…,x),其中随机变量X由个离散数据{x1,x2,…,x}组成,其边缘分布表示为F(x),其中∈[1,],那么存在一个Copula函数,使得

由于边缘累积函数F(x)为离散函数,则Copula函数只在区间[0,1]是唯一的。由式(5)可得,边缘累积函数=()为在区间[0,1]上均匀分布的函数,随机变量的联合累积分布函数(1,2,…,x)可由式(6)推导,因而可把Copula函数等效为在区间[0,1]上均匀分布的函数()的联合累积分布函数。并由此可得,经验Copula函数的计算如式(7)。


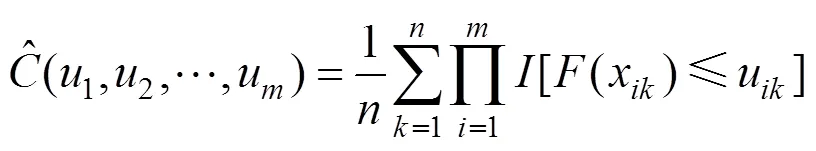
式中:(·)为示性函数,当(x)≤u时,[(x)≤u]=1,否则[(x)≤u]=0。
Copula函数的类型很多,应根据样本的分布特征选择合适的Copula函数[14]。本文选择常用的5类Copula建立不同结构的相关性模型,基本可以描述绝大多数变量间的相关关系,表1为各类型Copula函数及其表达式。

表1 常见Copula函数类型

以供电臂负荷AB有功数据为例,采用极大似然函数法,估计各类型Copula函数未知参数值[15]。可得Gumble-Copula,Frank-Copula,Clayton- Copula,正态-Copula和t-Copula函数的参数估计值分别为1.628 8,4.483 5,0.917 8,0.447 9和0.932 5,其中-Copula函数的自由度为4.386 9,由此完成5类Copula函数模型的建立。
2.2 Copula函数的优选
建立5类Copula 模型之后,需要根据优选指标选择最佳Copula函数作为牵引负荷联合分布模型,如表2所示。具体相关性指标包括:1) kendall秩相关系数:表示2种变量间变化趋势一致与否;2) Spearman 秩相关系数:表示2种变量间累积分布是否相同,这2个系数均可用于度量随机变量间的相关性;3) 欧氏距离:其值越小表示所建模型越贴合经验分布函数,式(9)为优选指标其值越小,表示所属模型与实际分布越接近。


式中:1,2和3分别表示Copula函数与样本数据的kendall、Spearman秩相关系数之差的绝对值和欧式距离,k为其指标的权重,可依次取0.2,0.2和0.6。

表2 相关性指标参数值
表2为5类Copula函数的指标参数值,代入式(9)可知,-Copula函数的优选指标值最小,说明其函数最接近实际分布,同时基于现场测量的数据驱动而建立的累积分布函数和Copula函数参数可以准确体现实际负荷特性,具有普遍适用性,并且样本的二元频率直方图(图5)与-Copula函数的概率密度分布(图6)基本一致,所以选择-Copula函数描述牵引负荷的相关性是精确的和适用的。
2.3 相关性模型生成
采用 Copula 函数生成具有相关性的牵引负荷模型主要分为 3 步:
1) 基于负荷实测数据,采用非参数核密度估计法建立边缘函数;
2)根据相关性指标选择最优 Copula 函数,采用抽样法生成在[0,1]上均匀分布的组符合相关性条件的随机数;
3)通过式(3)将生成的组随机数据转换为符合实际相关结构的相关性模型。
选用-Copula 函数描述负荷间功率的相关性最为精确和适用,并采用随机抽样法生成1 000组在区间[0,1]服从均匀分布且满足相关性条件的随机数,利用式(3)可模拟得具有相关性的牵引负荷模型。图7为模拟计及相关性的牵引负荷有功的散点图。同时,采用同样的采样方法模拟不计相关性的牵引负荷有功散点图,如图8所示。

图5 样本二元频率直方图
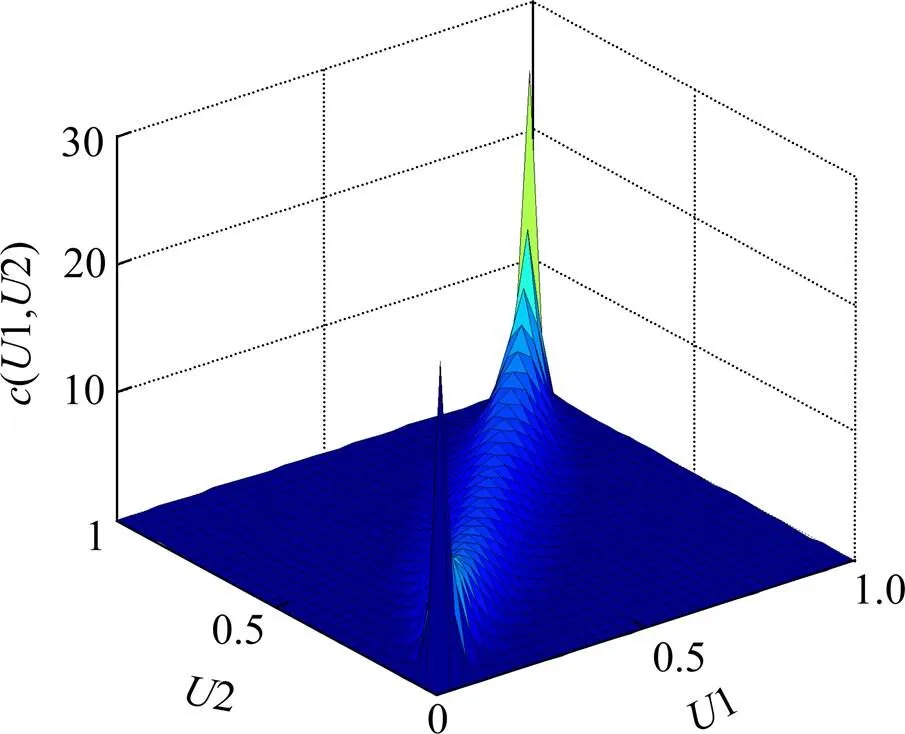
图6 t-Copula 概率密度分布

图7 模拟计及相关性的牵引负荷散点图

图8 模拟不计相关性的模拟牵引负荷散点图
3 计及牵引负荷相关性对电力系统影响
3.1 概率潮流计算过程
为了分析牵引负荷相关性对电力系统的影响,有必要建立计及相关性和不计相关性的负荷模型。对接入牵引负荷的系统进行潮流计算是研究负荷并网后对电力系统运行状态影响的基础。在牵引负荷相关特性与MCSM结合进行概率潮流计算的方法中,将计及相关性、不计相关性的模拟负荷和实测负荷(采样组)分别接入式(10)的系统潮流方程和支路功率方程,进行次重复的确定性潮流计算,再通过统计学方法得到电力系统的节点电压和支路功率的数字特征和分布曲线,可以比较准确地反映接入牵引负荷的电力系统潮流分布特征和状态变量(电压和潮流)的波动情况,并在此基础上分析计及牵引负荷相关性对电力系统的影响。
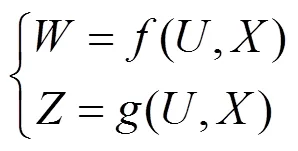
式中:为节点注入功率向量;为节点电压向量;为系统阻抗参数;为支路潮流向量。
3.2 牵引负荷准确性评估指标
为量化基于 Copula 理论建立的计及牵引负荷相关性模型在潮流计算中的准确性评估,在此采用3项指标对其进行准确性评估。
1) 相对误差指标ε用于评估所建模型在潮流计算中状态变量的数字特征偏差程度,数字特征包括期望值和标准差等;
2) 不平衡度均值指标ξ用于评估所建模型对接入点状态变量造成的三相不平衡程度,包括电压和电;
3) 根均值指标用于描述潮流计算中状态变量的累积波动程度。
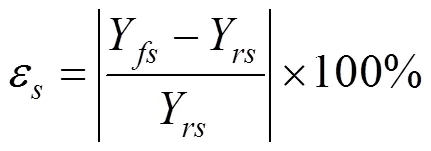
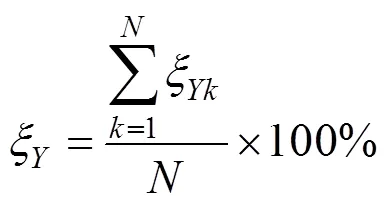

式中:和分别为状态变量数字特征的模拟值和实际值;和分别为状态变量累积分布函数上第个点的模拟值和实际值,为采样数。
4 算例仿真与分析
4.1 接入牵引负荷对电力系统的影响
为了验证本文所建相关性模型的准确性及其对电力系统的影响,将前文提及的牵引负荷接入IEEE-30 节点系统的节点21,其余负荷恒定。图9为IEEE-30节点系统拓扑。系统中平衡节点为节点1,其余电源节点均视为 PV 节点,系统容量基准值为100 MVA。
将基于Copula 理论构建的计及相关性、不计相关性模拟负荷和实测负荷(采样10 000组)接入IEEE-30节点系统进行概率潮流计算,再统计得到的节点电压和支路潮流的期望值和标准差等数字特征、概率密度和累积分布函数;根据图1搭建牵引负荷仿真模型,由于篇幅原因此处省略,仿真可得系统三相不平衡程度。图10~13分别给出了系统节点电压的数字特征,节点21,节点9和节点12的电压幅值的累积分布曲线和概率密度分布曲线。以电力系统的节点电压为例,分析牵引负荷对电力系统的影响。

图9 IEEE-30节点系统拓扑
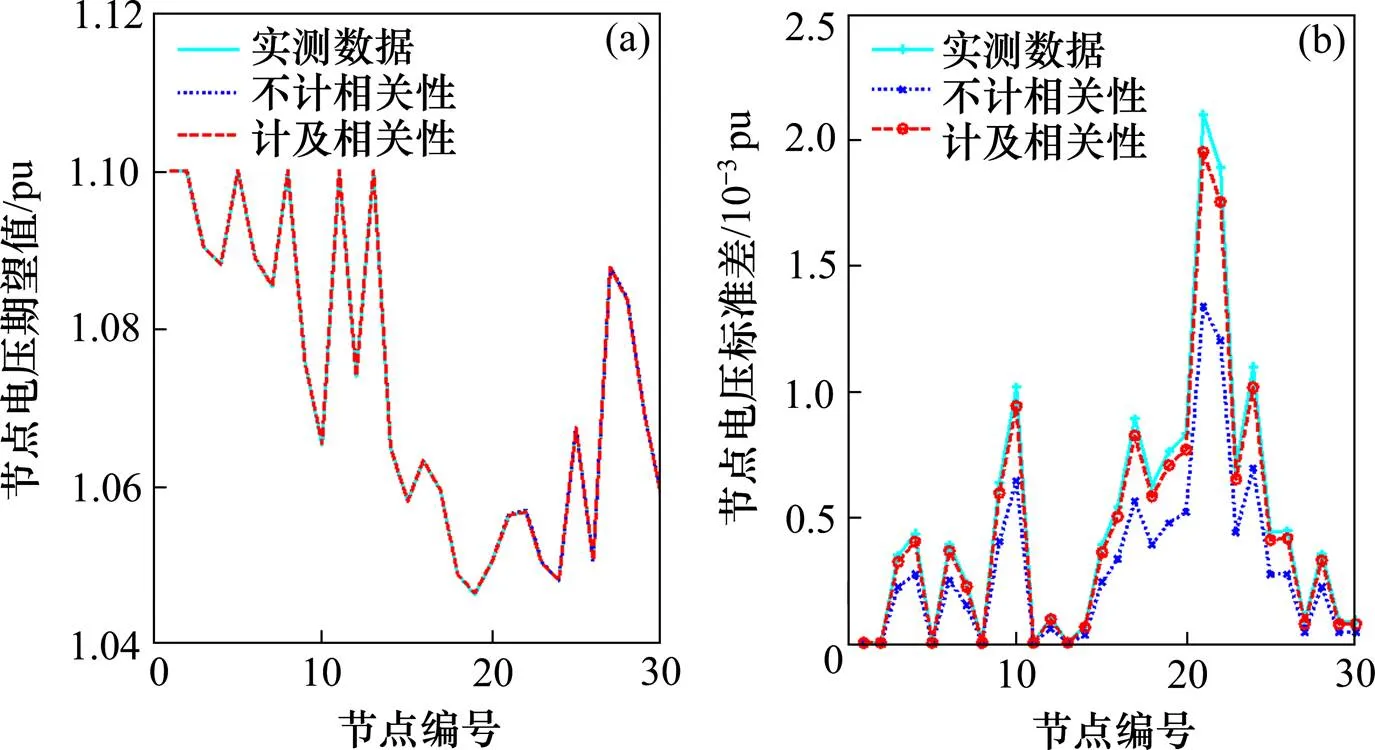
(a) 节点电压的期望值;(b) 节点电压的标准差
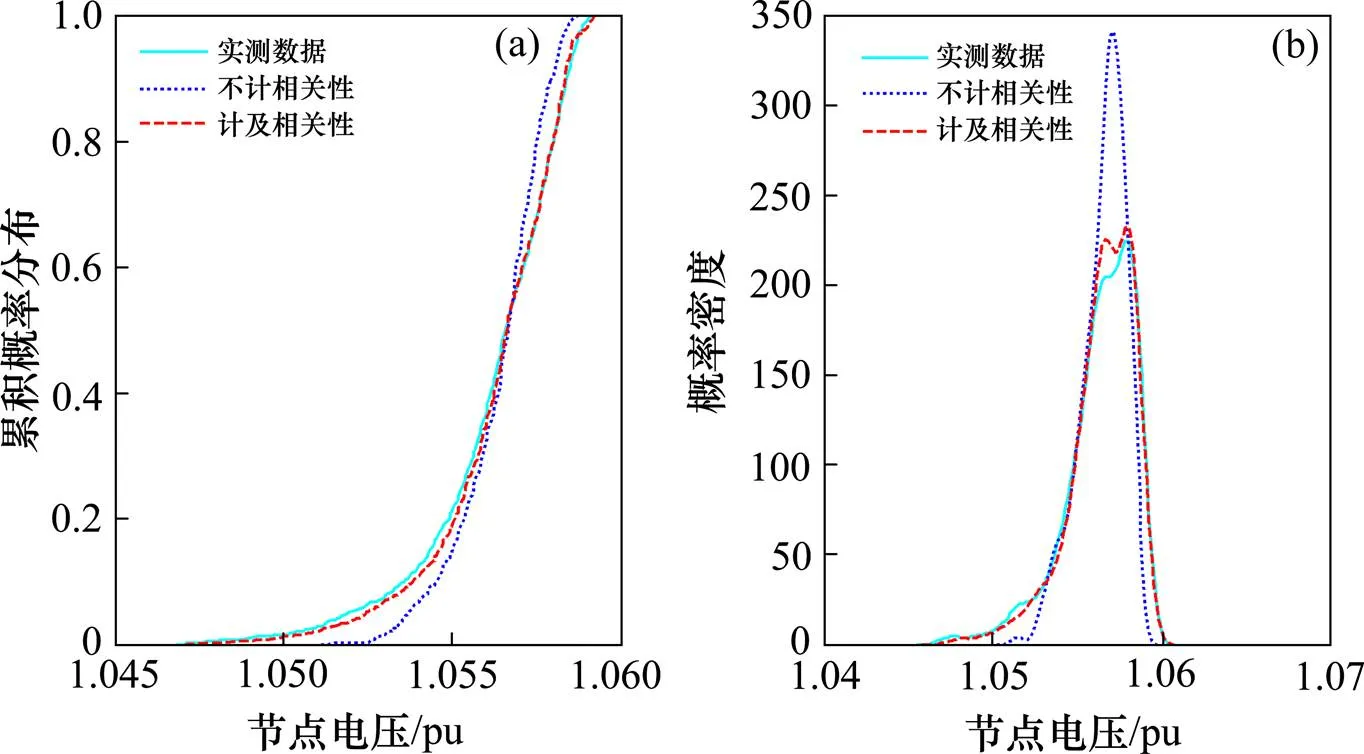
(a) 电压幅值累积分布;(b) 电压幅值概率密度分布

(a) 电压幅值累积分布;(b) 电压幅值概率密度分布
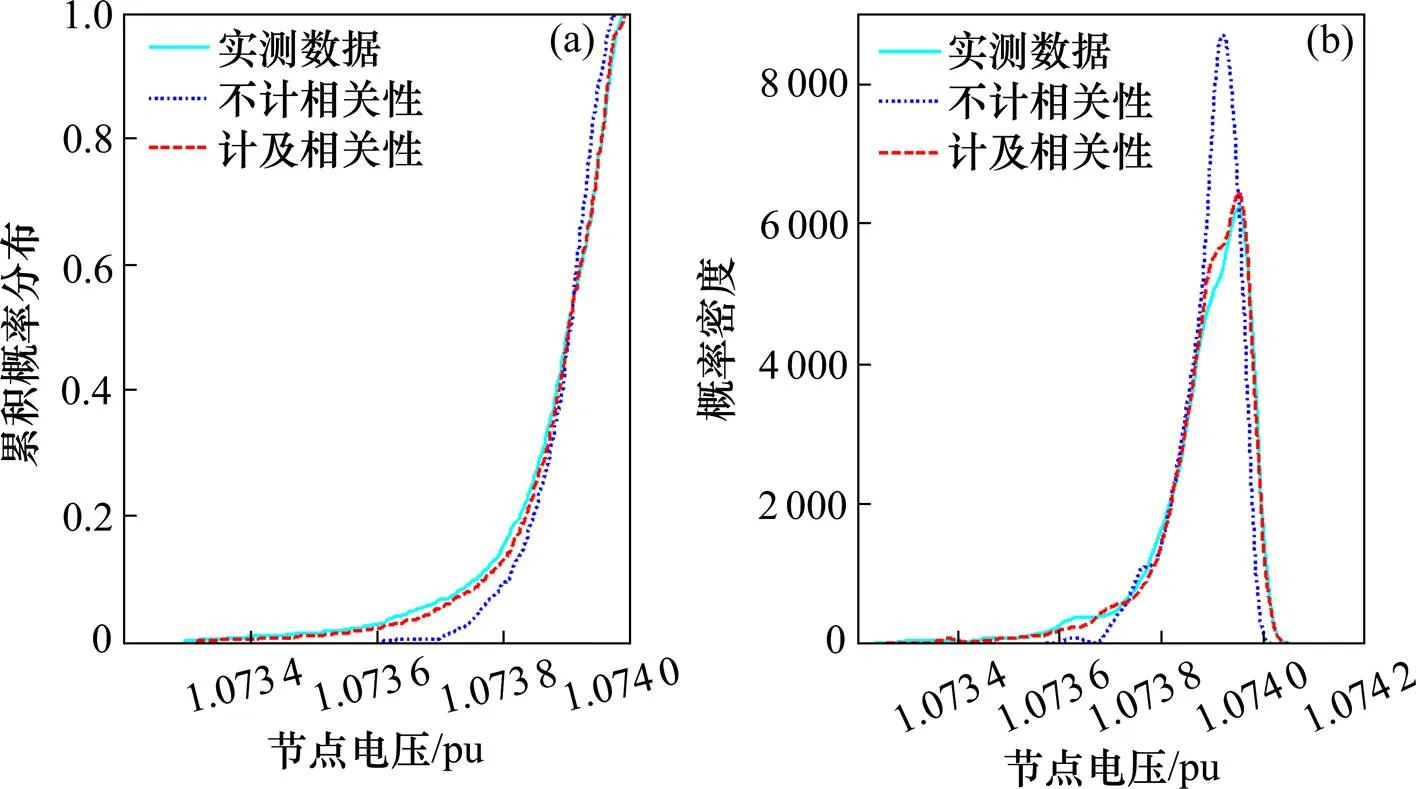
(a) 电压幅值累积分布;(b) 电压幅值概率密度分布
由图10可知,牵引负荷是否计及相关性对节点电压期望值几乎无影响,但计及负荷相关性的电压标准差明显更接近波动较大的实测数据,并且发现越是接近牵引负荷接入点(节点21)的节点,其电压数字特征的波动越是剧烈,说明牵引负荷会导致所在区域的电力系统较大波动。
在图11(a)中,不计相关性的电压幅值在 1.051 2~1.058 9间波动,而计及相关性和实测数据的电压幅值均在1.047 0~1.059 2区间变化且波动相对前者更大;在图12(a)中,不计相关性和计及相关性负荷的节点电压在1.074 1~1.764和1.072 7~1.076 5间波动;而在图13(a)中,两者的波动范围基本一致。由此可知,距离牵引负荷越远其潮流波动越小,相关性因素的影响也越小。在图11(b)中,计及负荷相关性的ε指标为7.20%,而不计相关性的ε指标为36.05%,同样,在图12(b)和13(b)中计及相关性的ε指标也远小于不计相关性,说明计及相关性的负荷累积分布在实测负荷附近上下浮动,函数分布比较平缓,而不计相关性的负荷则偏离实测负荷较远且变化比较剧烈,和实测数据的偏差较大。
所以,在潮流计算中不计牵引负荷相关性的潮流波动范围小但变化剧烈,和实际负荷偏差较大,而计及相关性的潮流波动范围大但变化平缓,显然更接近于实际负荷情况。
4.2 相关性模型的准确性验证
以牵引负荷实测数据计算结果为参考值,计及相关性和不计相关性的2组模拟结果为验证值。根据节点6电压和支路6-7潮流的数字特征进行偏差程度验证,评价指标包括期望值和标准差的相对误差指标ε衡量所提模型计算结果的偏差程度;状态变量的累积分布数据与期望值的根均值指标来衡量所提模型计算结果的波动程度;再根据负荷接入点的电力系统不平衡度ξ来反映牵引负荷模型所造成的电网测三相不平衡程度。

表3 状态变量偏差程度指标
根据表3中的ε指标,可知计及负荷相关性和不计负荷相关性的概率潮流计算的偏差指标差异很大,特别是前者的标准差的相对误差要比后者明显小很多,其他指标前者亦优于后者。说明计及负荷相关性比不计负荷相关性的潮流计算偏差更小,更贴近实测数据的计算结果。根据表4中的指标可以看出计及负荷相关性比不计负荷相关性中的潮流计算状态变量波动程度大,但更接近与实测数据的波动量,说明计及相关性的潮流计算更能反映实际的波动情况。
由表5可知,牵引负荷会引起网测系统的三相不平衡,包括三相电压和电流不平衡。计及相关性的负荷产生的不平衡度接近于实测负荷,而不计相关性的负荷会产生较大的三相不平衡度,对分析牵引负荷特性产生的不平衡影响的准确性不利。综上所述,计及负荷相关性所建立的模型的精确性更高,能更好的模拟牵引负荷的实际运行特性。

表4 状态变量波动程度指标

表5 状态变量不平衡程度指标
5 结论
1) 对于不规则分布的牵引负荷,可等效为两供电臂负荷的合成,采用Copula函数构建具有相关性负荷模型。由牵引负荷准确性评估指标可知,计及相关性比不计相关性的负荷模型波动更大、偏差更小和三相不平衡度更小,能更好的模拟牵引负荷的实际运行特性,仿真结果验证了所建模型的有效性和准确性。
2) 将计及相关性与不计相关性的模拟负荷与实测负荷的系统潮流结果对比分析,发现计及相关性导致所在区域的电力系统波动更大,但随距离的增加波动逐渐减弱,并且其潮流波动范围较大但变化平缓,更接近于实际牵引负荷情况。
[1] 杨强, 郝文斌, 洪行旅, 等. 考虑负荷时变性和动态补偿的电力系统负荷建模[J]. 电力系统保护与控制, 2011, 39(17): 17−21, 59. YANG Qiang, HAO Wenbin, HONG Xinglü, et al. Load modeling of power system considering time-variant load and dynamic compensation[J]. Power System Protection and Control, 2011, 39(17): 17−21, 59.
[2] 何洋阳, 黄康, 王涛, 等. 轨道交通牵引供电系统综述[J]. 铁道科学与工程学报, 2016, 13(2): 352−361. HE Yangyang, HUANG Kang, WANG Tao, et al. Railway passenger transportation development in China[J]. Journal of Railway Science and Engineering, 2016, 13(2): 352−361.
[3] 杨少兵. 电气化铁道牵引负荷概率分布特性与数学模型研究[D]. 北京: 北京交通大学, 2016: 29−57. YANG Shaobing. Probability distribution characteristics and mathematical models of traction power load of electrified railways[D]. Beijing: Beijing Jiaotong University, 2016: 29−57.
[4] 王芳, 王晓茹. 基于恒功率负荷的牵引供电系统潮流计算[J]. 电力系统及其自动化学报, 2015, 27(3): 59−64, 70. WANG Fang, WANG Xiaoru. A power flow analysis method of traction power supply system based on constant-power load[J]. Proceedings of the CSU-EPSA, 2015, 27(3): 59−64, 70.
[5] Trevor Williams, Curran Crawford. Probabilistic load flow modeling comparing maximum entropy and Gram- Charlier probability density function reconstructions[J]. IEEE Transactions on Power Systems, 2013, 28(1): 272−280.
[6] 王斌, 张民, 邱忠才, 等. 基于实测数据的高铁牵引变电所负序电流概率分析[J]. 西南交通大学学报, 2015, 50(6): 1137−1142.WANG Bin, ZHANG Min, QIU Zhongcai, et al. Probability analysis of negative phase-sequence current for high-speed railway traction substation based on measured data[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1137−1142.
[7] 高锋阳, 乔垚, 杜强, 等. 计及牵引负荷相关性的随机潮流计算[J]. 铁道学报, 2018, 40(10): 23−29.GAO Fengyang, QIAO Yao, DU Qiang, et al. Probability load flow calculation considering the correlation of traction load[J]. Journal of the China Railway Society, 2018, 40(10): 23−29.
[8] 韦艳华, 张世英.Copula理论及其在金融分析上的应用[M]. 北京: 清华大学出版社, 2008: 81−92. WEI Yanhua, ZHANG Shiying. Copula theory and its application in financial analysis[M]. Beijing: Tsinghua University Press, 2008: 81−92.
[9] Pagaefthymiou G, Kurowicka D. Using Copulas for modeling stochastic dependence in power system uncertainty analysis[J]. IEEE Transactions on Power Systems, 2009, 24(1): 40−49.
[10] WANG Yuankun, MA Huiqun, WANG Dong, et al. A new method for wind speed forecasting based on copula theory[J]. Environmental Research, 2018, 160(2018): 365−371.
[11] 刘丹丹. 考虑相关性的风电场等值及概率潮流计算研究[D]. 北京: 华北电力大学, 2017: 21−23. LIU Dandan. Research on equivalence of wind farms and probabilistic load flow calculation considering dependence[D]. Beijing: North China Electric Power University, 2017: 21−23.
[12] Rouhani M, Mohammadi M, Kargarian A. Parzen window density estimator-based probabilistic power flow with correlated uncertainties[J]. IEEE Trans Sustain Energy, 2016,7(3): 1170−1181.
[13] Nelsen R B. An introduction to Copulas[M]. 2nd Edition. New York, USA: Springer, 2006: 4−30.
[14] 吕颖, 鲁广明, 谢昶, 等. 考虑大规模集中接入风电功率波动相关性的在线概率安全评估[J]. 电网技术, 2018, 42(4): 1140−1148. LÜ Ying, LU Guangming, XIE Ying, et al. Online probabilistic security assessment considering centralized integration of large scale wind powe[J]. Power System Technology, 2018, 42(4): 1140−1148.
[15] ZHAI Jinjin, YIN Qilin, DONG Sheng. Metocean design parameter estimation for fixed platform based on copula functions[J]. Journal of Ocean University of China, 2017, 16(4): 635−648.
Probability model considering the correlation of traction load and its impact on power system
LUO Pei1, 2, XIE Yawen1, WEN Yan1
(1. School of Information Engineering, Xiangtan University, Xiangtan, 411105, China; 2. Institute of Energy Systems, Energy Efficiency and Energy Economics (ie3) TU Dortmund University, Dortmund, Germany)
In order to accurately describe the negative impact of the traction load’s correlation characteristics on the operation of the power system, this paper introduces Copula theory to build a correlated probability distribution model of the traction load, then to evaluates the operation of the power system with the load. Based on the measured load data, the cumulative distribution function is constructed by the non-parametric kernel density estimation method, and the best Copula function is selected according to the optimal index, and it is combined with the Monte Carlo simulation method to calculate the probabilistic load flow. Taking the measured load as the reference, the accuracy of the established correlation model is evaluated by the degree of deviation, imbalance and fluctuation. The simulated load with and without correlation and the measured load are connected to the IEEE-30 bus system in turn, the results showed that the correlated load as the measured load will cause large fluctuations in the power system, verfies that the proposed model is applicable and accurate, and provides reference value for the safe operation of the system.
traction load; correlation; Copula theory; power system; probabilistic load flow
TM922
A
1672 − 7029(2020)04 − 1004 − 11
10.19713/j.cnki.43−1423/u.T20190628
2019−07−13
湖南省自然科学基金资助项目(2018JJ2397);中国国家留学基金管理委员会(CSC)资助项目(201808430009)
罗培(1974−),男,湖南沅江人,教授,博士,从事电力系统电能质量控制研究;E−mail:lpmq@163.com
(编辑 蒋学东)

