隧道侧方基坑对隧道上方围岩压力拱的影响
高 峰, 齐怀远, 张 捷, 唐 星, 唐宇辰, 黄 磊
(1.重庆交通大学土木工程学院,重庆 400074;2.重庆市潼南区港航管理处,重庆 402660)
在城市化进程中,随着地面、高层和地下建筑同时发展,出现了除地铁外越来越多的地下空间及设施,此时,大量的基坑工程也就产生[1]。在各种建筑基坑工程附近修建地铁隧道及在既有地铁隧道附近修建建筑基坑的邻近工程情况变得越来越普遍。而邻近工程通过土体来对彼此的稳定性和结构性能进行影响,因此,隧道与基坑相邻工程的安全稳定性研究意义重大。围岩良好的稳定性是保证隧道安全性能的重要基础,在设计施工中,技术人员根据地勘资料确定围岩等级及相关参数,以便判定围岩能否形成“压力拱”,以便设计人员合理且经济地设置衬砌材料参数和运用支护手段,故“压力拱”是岩土地下工程中最经济、最可靠的判定围岩稳定性的方法之一[2]。
近年来,诸多学者和工程技术人员已在基坑开挖对邻近地铁隧道的影响及隧道围岩压力拱方面进行了诸多研究。Peck教授在统计分析了现场实测的许许多多地表沉降数据之后提出了普遍被大家熟知的高斯分布曲线;杨新锐[3]在借鉴高斯分布曲线后对软土地区隧道开挖引起的地层变形进行了研究;Mana等[4]、Leung等[5]认为墙体水平位移中的最大值与竖向位移中的最大值之间必然存在某种关系;邓旭[6]认为到基坑围护桩的水平形变必然与水平横撑和基坑对称性有关;邹伟彪等[7]、张治国[8]于在建基坑工程的基础上,得出基坑工程现场监测数据值与数值模拟计算结果值基本吻合,认为数值建模可靠性较高;魏少伟[9]认为在其余条件不变的情况下,隧道在靠近基坑连续墙一侧的变形趋于向基坑中心旋转;李珏池[10]对浅埋软岩隧道失稳机理及塌方的处理进行了研究;姜兆华[11]分析研究了基坑开挖过程中与其相邻的既有隧道的内力和变形受影响的大致变化规律。
现有关于基坑开挖对邻近隧道影响研究多是从位移变形和地表沉降直接探测其影响,鲜有研究从围岩“压力拱”来分析基坑对侧方隧道上方围岩稳定性影响。针对基坑开挖从应力路径的角度去分析隧道上方压力拱受基坑开挖深度、开挖宽度、基坑与隧道净距等多个因素影响下压力拱内、外边界的变化规律,为隧道邻近基坑施工时的稳定性和安全性研究提供新的思路。
1 压力拱相关理论
1.1 压力拱的形成过程

图1 隧道开挖前后的主应力矢量对比Fig.1 Comparison of principal stress vectors before and after tunnel excavation
压力拱实际上是由于初始岩土体受开挖扰动而产生形变,产生“土拱”现象,并且“土拱”能承受其自身及上方围岩压力且能传递部分围岩压力,使得松散岩土体应力的偏转即产生应力重分布而形成的一种围岩力学现象。如图1所示,隧道开挖前岩体中的最大主应力方向均为竖直的,而隧道开挖之后,隧道开挖面附近的围岩主应力方向明显发生了偏转,且最大主应力呈现出“环状体”的形式,尤其是拱顶正上方和仰拱最下方最大主应力的方向呈水平方向,此“环状体”即为压力拱。
1.2 压力拱的判定方法
1.2.1 应力路径
在隧道拱部正上方、拱腰一侧及底部仰拱正下方,将3个方向分别定义3条不同的路径,分别为路径1、路径2、路径3,如图2所示。从这3条不同的路径上的应力变化情况来详细分析隧道开挖后周围的围岩应力重分布规律。路径的起点均为隧道开挖面边缘点,终点均为模型边缘。
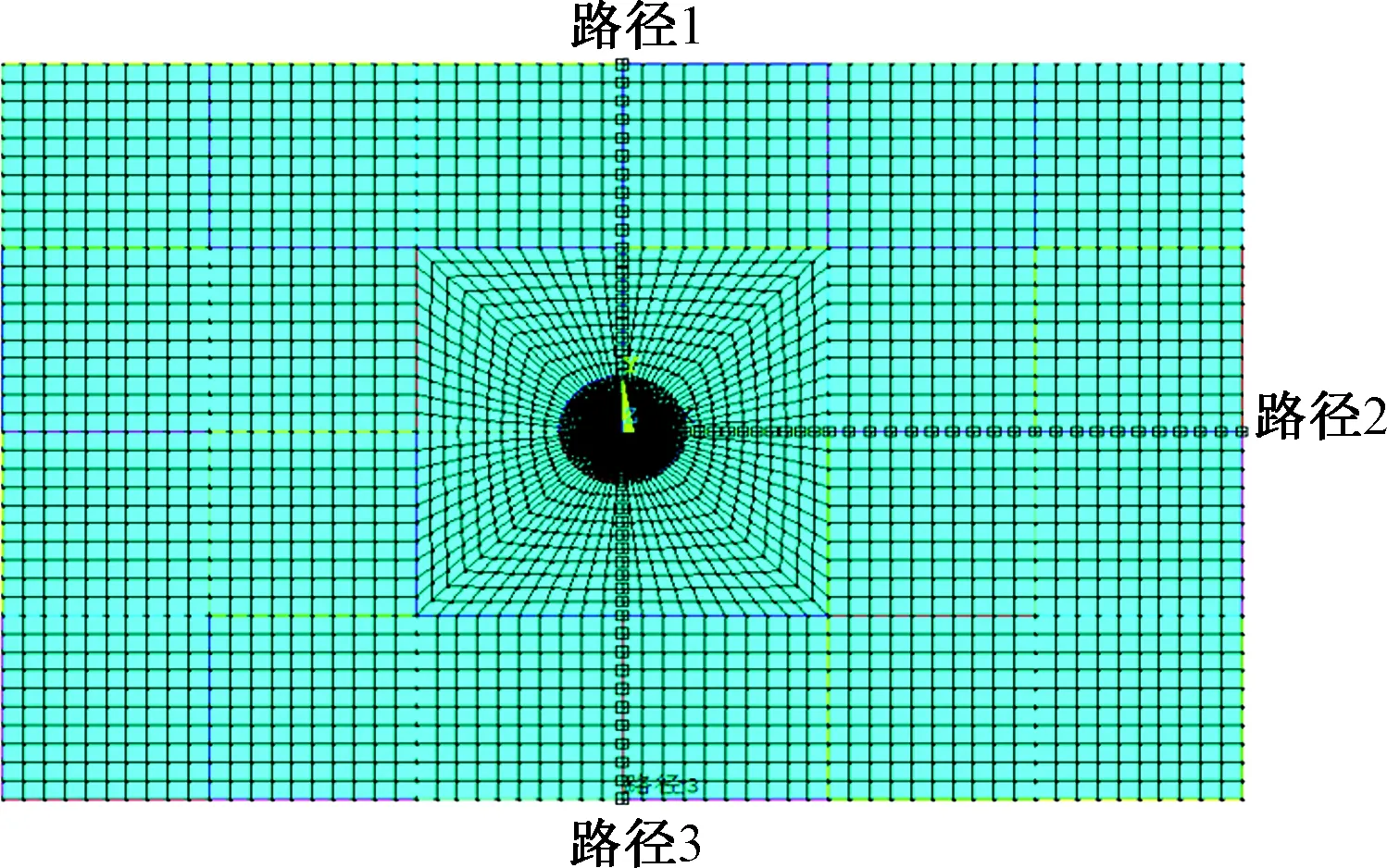
图2 应力路径示意图Fig.2 Schematic diagram of the stress path
基于本文只考虑隧道上方围岩压力拱的研究,故本节仅针对路径1进行分析。
1.2.2 路径1上压力拱内外边界的确定
现从应力路径和应力变化规律两个方面来判定压力拱的内、外边界。
(1)用应力路径分析法可以确定隧道拱顶上方路径1压力拱的内边界判定方法为:最大主应力的最大值处即为压力拱的内边界点,如图3所示。

图3 开挖后路径1最大主应力云图Fig.3 Maximum principal stress cloud map of path 1 after excavation
(2)压力拱外边界的判定:在压力拱截面内最大主应力矢量为水平向,在压力拱截面外最大主应力矢量为垂直向,即最大主应力在压力拱外边界发生偏转,由水平应力偏转为垂直应力,因此,压力拱外边界点必然是最大主应力的偏转点。但是由于有限元网格划分的密度和单元类型等因素的影响,数值计算不易得出最大主应力的精确偏转位置点,利用“相对指标法”[12],其公式为
δ=(σmax-σ22)/σmax
(1)
式(1)中:σmax为最大主应力;σ22为垂直应力。
当δ=0%时,最大主应力矢量偏转为垂直向,在此引入路径4,如图4所示,即除路径1外拱顶外其余节点处虽存在向垂直方向偏转,但未出现如路径1上偏转为垂直方向的点存在,李奎[12]提出,当δ<5%时最大主应力矢量方向有逐渐恢复为垂直向趋势,而对于δ>5%时不计相对偏转指标表示的物理意义。
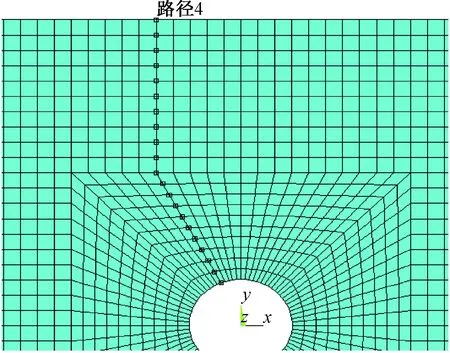
图4 路径4示意图Fig.4 Schematic diagram of path 4
基于普遍适用的原则,取相对偏转指标δ=5%时该点所对应的与隧道拱顶的距离为压力拱的外边界值。
开挖前后路径1应力路径曲线如图5所示。
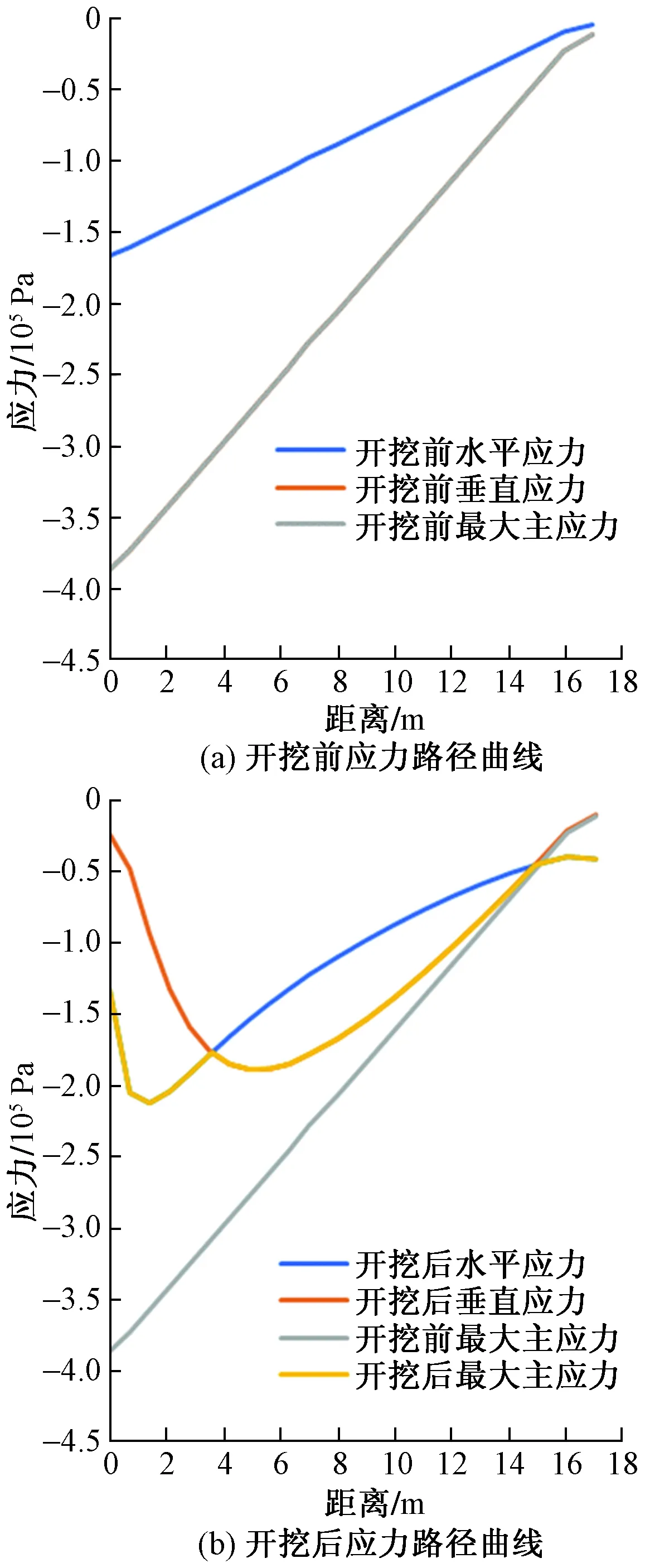
图5 开挖前后路径1应力曲线Fig.5 Stress curve of path 1 before and after excavation
2 数值模拟
2.1 土体及支护体系的有限元模型及相关参数
采用有限元软件ANSYS进行数值模拟,按平面应变问题建立数值模型,本构关系为理想弹塑性模型,屈服准则为Drucker-Prager屈服准则,土体采用4节点平面单元 PLANE42模拟,隧道和基坑开挖均采用“杀死单元”来实现,地下连续墙和隧道衬砌材料均采用梁单元BEAM3模拟,连续墙和衬砌材料的施加均采用“激活单元”来实现。
实体模型中隧道断面参考某地铁区间马蹄形断面,洞径为10 m,埋深为25 m,基坑的长边与隧道的纵向互相平行。基坑的相关尺寸为变量,即基坑开挖深度、基坑开挖宽度、基坑与隧道的净距。
整个模型以隧道开挖面的中心点来建立,并根据试算,排除边界条件的影响,选定平面模型的尺寸为140 m×70 m。边界条件为:模型的上边界即Y=30 m的面设置为自由面;模型的下边界即Y=-40 m的面,施加Y方向的位移约束;模型的左右边界面即X=-50 m和X=90 m的面,施加X方向的位移约束。各材料参数如表1所示,有限元模型的网格划分如图6所示。

表1 材料参数

图6 有限元模型网格划分Fig.6 Finite element model meshing
2.2 数值模拟实施步骤
2.2.1 既有基坑对侧方新建隧道压力拱影响模拟的实施步骤
(1)建立整个土体及支护结构(地下连续墙)的有限元模型。
(2)“杀死”所有支护结构单元,并施加重力荷载,模拟土体在自重作用下的自由沉降,即自重应力求解。
(3)施加基坑开挖前围护结构并进行基坑开挖。“激活”地下连续墙单元并逐层“杀死”各层的土体单元,模拟既有基坑。
(4)静力分析求解计算。
(5)隧道全断面开挖。“杀死”隧道开挖面所有单元,不施作初期支护,围岩压力全部释放,模拟隧道毛洞开挖后支护前的应力状态。
(6)静力分析求解计算。
(7)提取路径1计算数据,得到相关结果。
2.2.2 基坑开挖对侧方既有隧道压力拱影响模拟的实施步骤
(1)建立整个土体及支护结构(隧道衬砌、地下连续墙)有限元模型。
(2)“杀死”所有支护结构单元,并施加重力荷载,模拟土体在自重作用下的自由沉降,即自重应力求解。
(3)隧道全断面开挖,施加等效荷载,“激活”隧道衬砌单元,模拟既有隧道。
(4)静力分析求解计算。
(5)“激活”“连续墙单元”并“杀死”基坑各层的土体单元,模拟基坑开挖施工的过程。
(6)静力分析求解计算。
(7)提取路径1计算数据,得到相关结果。
3 既有基坑对新建隧道围岩压力拱及基坑开挖对既有隧道围岩压力拱的影响分析
3.1 无基坑情况下的隧道开挖压力拱
当无基坑时,隧道处于开挖后支护前的应力状态下,提取拱顶上方路径1的计算数据,其数值的计算结果如表2所示,其变化趋势如图7所示。

表2 路径1压力拱计算结果

图7 无基坑情况下的隧道开挖后应力变化Fig.7 Stress change after tunnel excavation without foundation pit
3.2 既有基坑深度对新建隧道压力拱的影响
基坑与隧道之间的净距取11 m,基坑宽度取20 m,基坑深度尺寸分别取4、8、12、16、20、26、28、32 m共计8个变量值,采用单一变量法分别建模求解。
拱顶上方路径相关应力曲线如图8所示。既有基坑开挖深度对侧方隧道全断面开挖后支护前拱顶围岩压力拱的内、外边界值及其对应的增加值如图9及表3所示。3.3~3.8节仅列出计算结果。
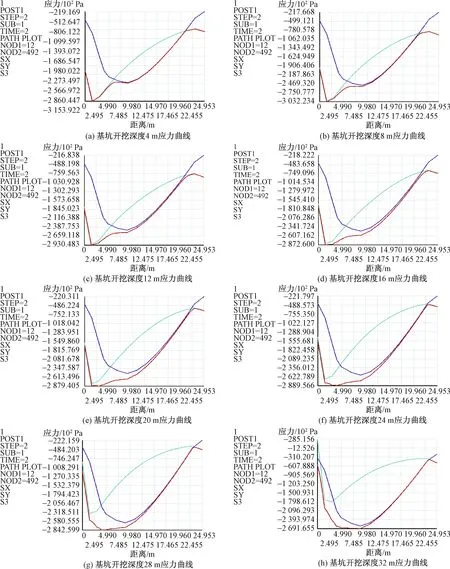
图8 基坑开挖深度4~32 m应力曲线Fig.8 4~32 m stress curve for foundation pit excavation depth
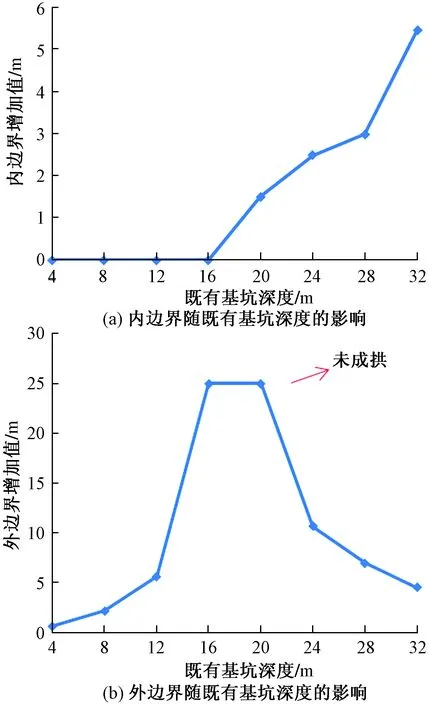
图9 既有基坑深度对新建隧道压力拱影响的计算结果Fig.9 Calculation result of influence of foundation pit depth on pressure tunnel of new tunnel
处于开挖后支护前状态下的隧道拱顶上方围岩压力拱随侧方既有基坑深度的影响规律总结如下。
(1)侧方既有基坑开挖深度对新建隧道拱顶压力拱内边界的影响规律为:在某一合理的较浅(较隧道埋深而言)深度范围内,随着基坑开挖深度的增加,压力拱内边界不受开挖深度的影响,均为隧道单独开挖时的内边界值,但是基坑深度一旦超过某一临界值,内边界将持续增加,意味着隧道开挖面与压力拱内边界之间的范围越来越大,围岩的变形量急剧增加,围岩压力增加,隧道稳定性降低。本例中取0.7倍的隧道埋深为内边界增加临界基坑深度值。
(2)侧方既有基坑开挖深度对新建隧道拱顶压力拱外边界的影响规律为:在某一合理的较浅(较隧道埋深而言)深度范围内,随着基坑开挖深度的增加,压力拱外边界虽成比例增加,但始终具备一定自稳能力;当既有基坑深度增加到0.56~0.88倍的隧道埋深范围内,外边界迅速增加到地面以上,围岩受埋深限制无法形成安全有效的压力拱,隧道由“深埋”变“浅埋”,围岩压力突增,自稳能力急剧下降,隧道稳定性降低。在基坑深度超过0.88倍的隧道埋深后,外边界逐渐回落形成压力拱。
(3)随着既有基坑深度的增加,较无基坑情况下的隧道围岩压力拱而言,其内、外边界整体呈现不同程度的增加,围岩稳定性降低。
3.3 既有基坑宽度对新建隧道压力拱的影响研究
既有基坑深度取12 m,基坑与新建隧道的净距取11 m,基坑宽度取12、16、20、24、28、36、40、42、44、48 m共计10个数值,采用单一变量法分别建模求解。

表3 既有基坑深度对新建隧道压力拱影响的计算结果
既有基坑开挖宽度对侧方隧道全断面开挖后支护前拱顶围岩压力拱的内外边界值如表4所示。
处于开挖后支护前应力状态下的隧道拱顶上方围岩压力拱随侧方既有基坑宽度的影响规律总结如下。
(1)侧方既有基坑开挖宽度对新建隧道拱顶压力拱内边界的影响规律为:在某一合理的较小(较隧道跨径而言)宽度范围内,随着基坑开挖宽度的增加,压力拱内边界不受开挖深度的影响,均为隧道单独开挖时的内边界值,但是基坑宽度一旦超过某一临界值,内边界将增加,隧道稳定性降低。本例中取3.4倍的隧道跨径为内边界增加的临界基坑宽度值。
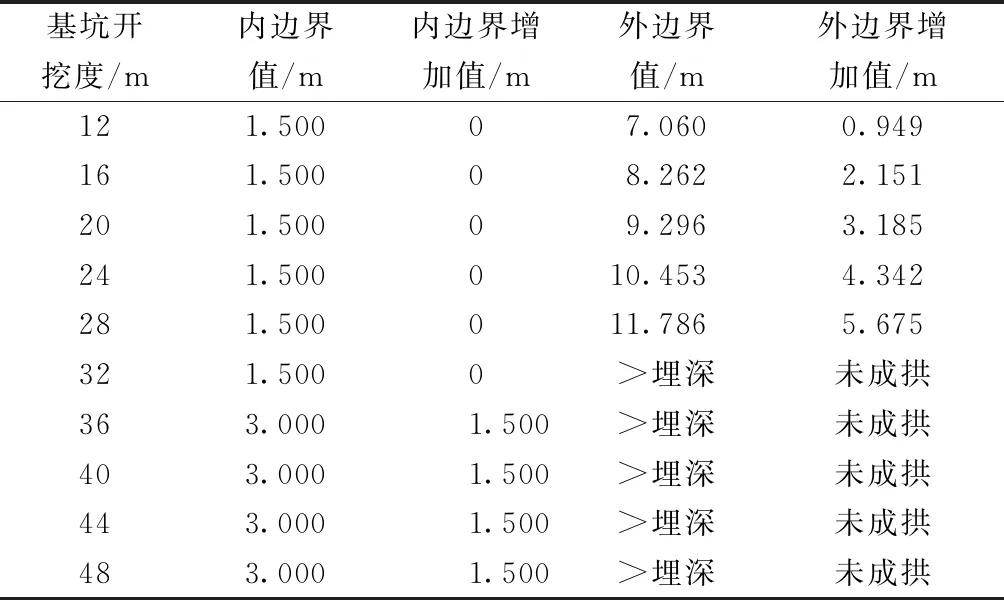
表4 既有基坑宽度对新建隧道压力拱影响的计算结果
(2)侧方既有基坑开挖宽度对新建隧道拱顶压力拱外边界的影响规律为:在某一合理的较小(较隧道跨径而言)宽度范围内,随着基坑开挖宽度的增加,压力拱外边界虽成比例增加,但始终能形成压力拱,具备较强的自稳能力;当既有基坑宽度超过某一临界值,外边界迅速增加到地面以上,无法形成安全有效的压力拱,隧道由“深埋”变“浅埋”,隧道稳定性降低。本例中取3倍的隧道跨径为是否顺利成拱的临界基坑宽度值。
(3)随着基坑宽度的增加,压力拱内、外边界整体呈现不同程度的增加,围岩稳定性降低。
3.4 基坑与隧道净距对新建隧道压力拱的影响
基坑的开挖深度取12 m,基坑的开挖宽度取20 m,基坑与隧道的净距分别取5、7、9、11、13、15、17、19、21、23、25、27、29、31 m共14个数值,采用单一变量法分别建模求解。
侧方隧道全断面开挖后拱顶围岩压力拱的内外边界值如表5所示。
处于开挖后支护前状态下的隧道拱顶上方围岩压力拱随侧方既有基坑与隧道之间净距的影响规律总结如下。
(1)净距对隧道拱顶压力拱内边界的影响规律总结为:随着既有基坑与隧道净距的增加,在某一合理的较大净距范围内,压力拱内边界不受净距的影响,但是净距一旦小于某一临界值,内边界将增加,隧道稳定性降低。本例将10 m净距值作为本例中隧道压力拱内边界增加的临界值。
(2)净距对隧道拱顶压力拱外边界的影响规律总结为:在超过某一合理的临界净距之外,隧道净距的增加,压力拱外边界值不受影响,即接近无基坑状态时的压力拱外边界值基本不变;围岩自稳能力较好;当间距小于这个临界的净距时,外边界迅速增加到地面以上,无法形成安全有效的压力拱,隧道由“深埋”变“浅埋”,隧道稳定性降低。本例将12 m净距作为本例中隧道是否顺利成拱的临界净距值。
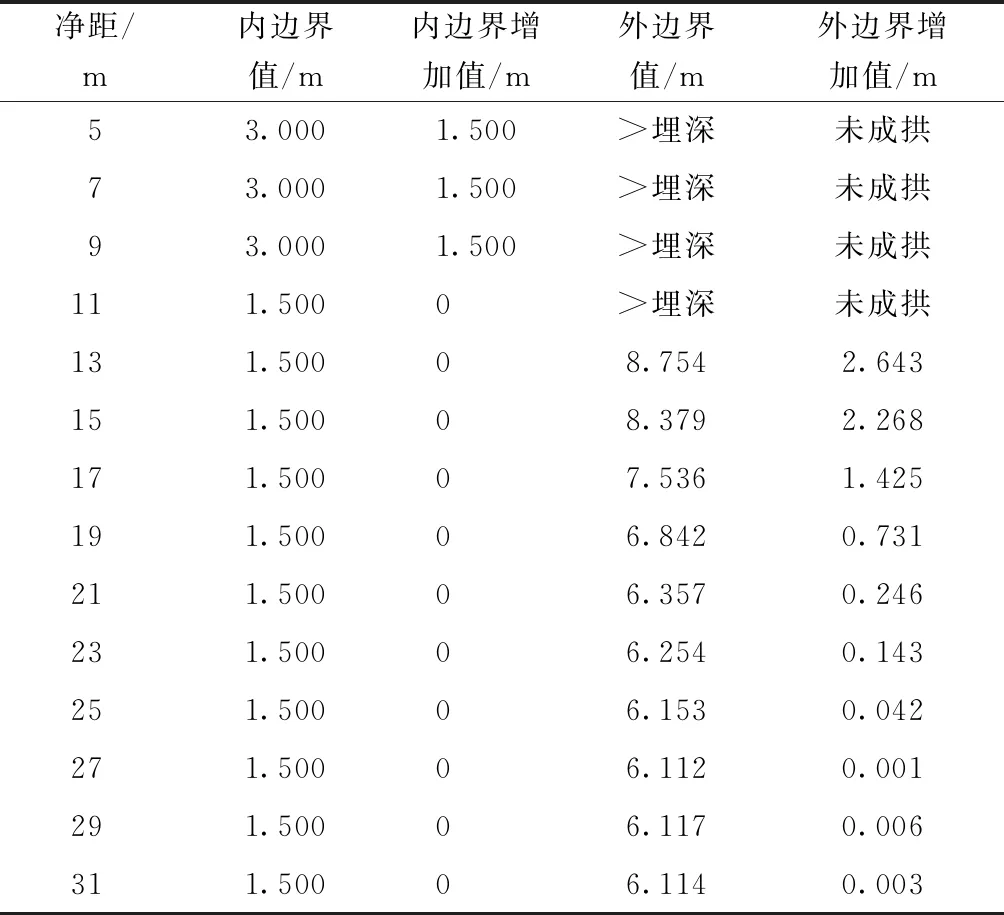
表5 不同净距下隧道拱顶上方压力拱计算结果
(3)随着净距的减小,较无基坑情况下的隧道围岩压力拱而言,其内、外边界整体呈现不同程度的增加,围岩稳定性降低。
3.5 无基坑情况下的既有隧道压力拱研究
当无基坑时,隧道处于支护稳定后的应力状态下,提取拱顶上方路径1的计算数据,其数值的计算结果如表6所示,其变化趋势与3.1节相同。
将表6对比表2可知,处于开挖后支护前应力状态下的新建隧道而言,压力拱内边界不变,外边界减小,压力拱厚度减小,因此可以认为,衬砌材料的施加可有效减小压力拱厚度,有助于隧道围岩稳定性的提高。
3.6 基坑开挖深度对既有隧道压力拱的影响
各参数同3.2节,采用单一变量法分别建模求解。新建基坑开挖深度对侧方既有隧道拱顶围岩压力拱的内外边界值如表7所示。
处于支护稳定后状态下的既有隧道拱顶上方围岩压力拱随侧方新建基坑开挖深度的影响规律总结如下。

表6 路径1压力拱计算结果
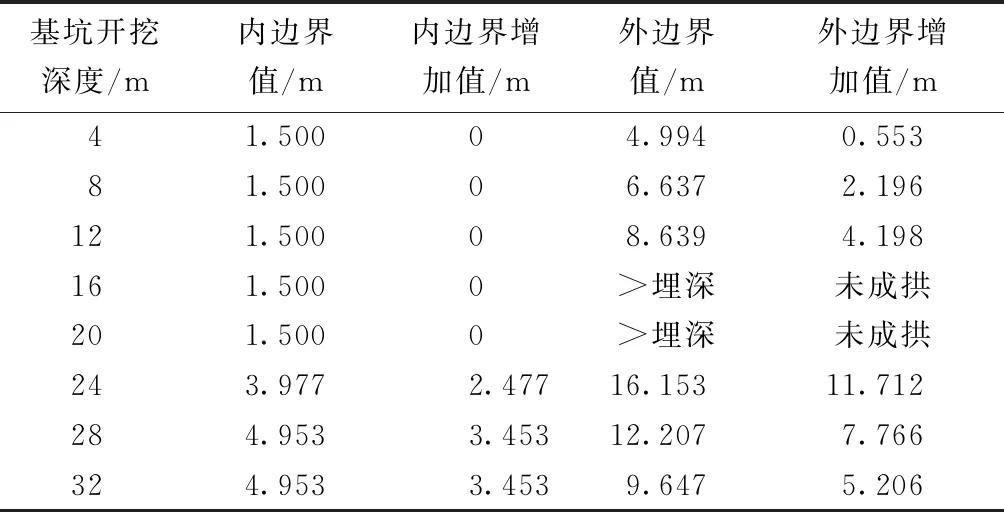
表7 基坑开挖深度对既有隧道压力拱影响的计算结果
(1)侧方新建基坑开挖深度对既有隧道拱顶压力拱内边界的影响规律与3.2节相比内边界增加临界值提高,本例中取0.9倍的隧道埋深为内边界增加临界基坑深度值。
(2)侧方新建基坑开挖深度对既有隧道拱顶压力拱外边界的影响规律与3.2节类似。
(3)既有隧道压力拱内边界受侧方基坑开挖宽度的影响敏感度远远低于3.2节当中的新建隧道上方围岩压力拱的内边界受既有基坑深度的影响敏感度;外边界受基坑开挖宽度的敏感度近似相同。
3.7 基坑开挖宽度对既有隧道压力拱的影响
各参数同3.3节,采用单一变量法分别建模求解。既有基坑开挖宽度对侧方既有隧道拱顶围岩压力拱的外边界值如表8所示。
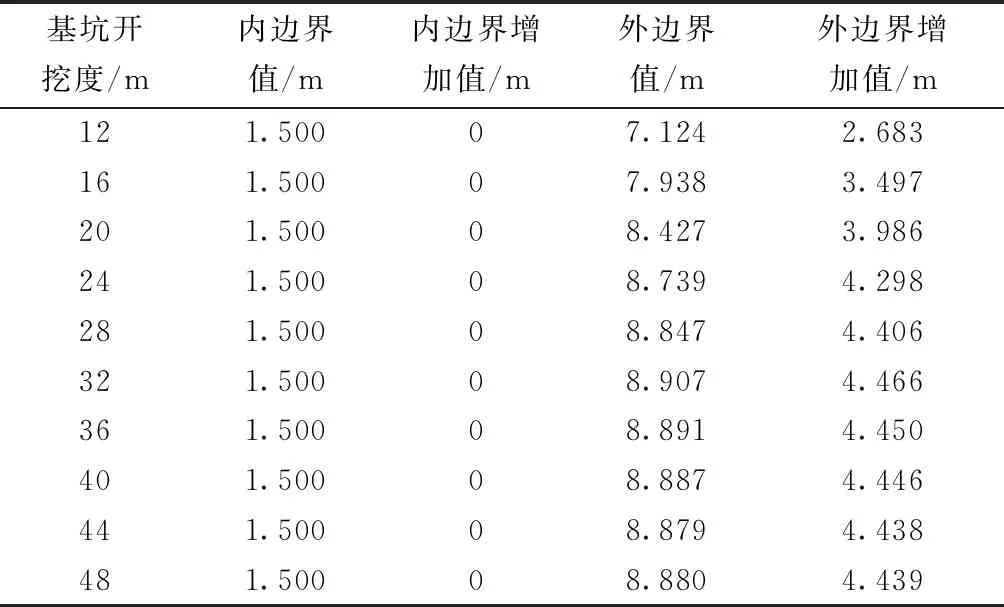
表8 基坑开挖宽度对既有隧道压力拱影响的计算结果
既有隧道拱顶上方围岩压力拱随侧方基坑开挖宽度的影响规律总结如下。
(1)基坑开挖宽度对既有隧道压力拱内边界的影响规律为:随着隧道侧方既有基坑宽度的增加,拱顶上方压力拱内边界整体呈现稳定不变的趋势,可以认为,在既定的围岩等级、隧道跨度、隧道埋深、基坑深度、基坑与隧道之间净距的情况下,既有隧道上方围岩压力拱内边界不受侧方基坑宽度的影响。
(2)基坑开挖宽度对既有隧道压力拱外边界的影响规律为:在某一合理的较小(较隧道跨径而言)宽度范围内,随着基坑开挖宽度的增加,拱顶上方压力拱外边界呈现等比增加的趋势;当基坑开挖宽度超过某一临界值,基坑开挖宽度越大,外边界增加值有稳定不变的趋势,所以外边界值不变;本例中当基坑开挖宽度为3倍的隧道跨径值时,隧道上方外边界达到最大值,之后随着基坑开挖宽度的增加,外边界保持不变,且始终无不成拱的情况发生。
(3)既有隧道压力拱内外边界受侧方基坑开挖宽度的影响敏感度远远低于3.3节当中的新建隧道上方围岩压力拱的内外边界受既有基坑宽度的影响敏感度。
3.8 基坑与隧道净距对既有隧道压力拱影响
各参数同3.4节,采用单一变量法分别建模求解。侧方隧道全断面开挖后拱顶围岩压力拱的内外边界值如表9所示。

表9 不同净距下隧道拱顶上方压力拱计算结果
既有隧道拱顶上方围岩压力拱随侧方基坑与隧道净距的影响规律总结如下。
(1)净距对既有隧道拱顶压力拱内边界的影响规律总结为:在某一合理的较大净距之外,压力拱内边界不受净距变化的影响,但是净距一旦低于这一临界值,内边界将明显增加,内边界与衬砌结构之间的松动围岩范围增加,衬砌材料承担的围岩压力增加。将6 m净距值作为隧道压力拱内边界增加的临界值。
(2)净距对既有隧道拱顶压力拱外边界的影响规律总结为:大于某一合理的临界净距后,隧道净距变化对压力拱外边界值不造成影响;当净距在低于临界值的一定范围内减小,外边界有明显的增加,围岩稳定性降低,但始终存在自稳能力;当净距低于另一较小的临界净距,压力拱外边界迅速增加到地表以上,无法形成安全有效的压力拱,隧道处于浅埋状态,衬砌材料所承受的围岩压力急剧增加。将10 m净距作为本例中是否顺利成拱的临界净距值。
(3)既有隧道压力拱内外边界受侧方基坑净距的影响敏感度略低于3.4节当中的新建隧道上方围岩压力拱的内外边界受既有基坑净距的影响敏感度。
4 基坑影响下隧道垂直均布压力计算方法及应用
4.1 考虑侧方基坑影响下的隧道垂直均布压力计算方法
据前面章节分析,基坑与隧道的净距、基坑深度及宽度都会使得隧道压力拱内外边界受到影响,尤其是:①内边界的增加;②外边界增加到地表之上,围岩受埋深限制无法形成压力拱。根据基于弹塑性理论可得,压力拱是否形成,是判定隧道“深浅埋”的重要依据,深埋和浅埋状态下的隧道围岩压力值存在差异,决定了衬砌材料是否满足安全稳定性要求。由现规范可知,隧道上方围岩垂直均布压力方法如下。
(1)判定外边界是否形成,隧道上方围岩是否顺利成拱。
(2)若成拱,依据压力拱内边界的增加计算突变后的隧道垂直均布压力。
围岩压力拱内边界与隧道开挖面之间的岩体为松动岩体,内边界值的大小可反映松动围岩范围的大小,故分析隧道压力拱随侧方基坑内边界值的变化,可判定松动围岩范围的变化大小及确定隧道上方围岩压力的变化情况。针对内边界变化所引起的围岩压力的变化情况,引入“内边界增加值”这个概念,用Δh来表示。Δh的计算方法为
Δh=h′-h0
(2)
式(2)中:h′为受基坑影响后的内边界值,m;h0为无基坑时压力拱的内边界值,m。
参考《公路隧道设计规范》(JTG D70—2014)[13]及《铁路隧道设计规范》(TB10003—2016)[14]可知深埋隧道垂直均布压力q的计算公式为
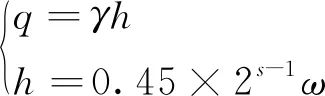
(3)
式(3)中:q为围岩垂直均布压力,kN/m2;γ为围岩重度,kN/m3;s为围岩级别;ω为宽度影响系数,ω=1+i(B-5),B为隧道宽度,m,i为隧道宽度的影响系数,当B<5 m时,取i=0.2,B>5 m时,取i=0.1。
受基坑影响后,若隧道围岩压力拱依然存在,但内边界增加,必然引起围岩压力突增,突增后的围岩压力计算方法考虑内边界增加值Δh,计算隧道结构竖向荷载值q′的公式为
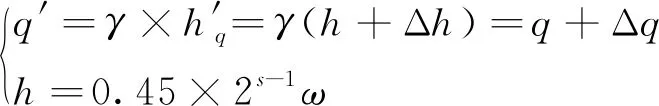
(4)
式(4)中:h′q为受基坑影响后竖向等效荷载高度值,m。
(3)若不成拱,则“深埋”变“浅埋”计算突增后的隧道垂直均布压力。
由第3章可知,当外边界受各因素的影响迅速增加到地表以上,隧道上方围岩受埋深限制无法成拱,也就意味着此时由“深埋”变为“浅埋”,式(3)的计算方法不再适用该“浅埋”隧道,而应该采用浅埋隧道围岩压力计算,方法如下。
按荷载等效高度的判定公式为
HP=(2~2.5)hq
(5)
在矿山法施工的条件下,对于Ⅳ-Ⅵ级围岩而言,取
HP=2.5hq
(6)
式中:HP为浅埋隧道分界深度,m;hq为荷载等效高度,m,按下式计算:
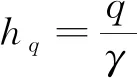
(7)
当压力拱无法形成时,隧道不能按深埋隧道只考虑坍落拱高度范围的竖向荷载,而是应该按照浅埋隧道来计算围岩压力,其方法分为下述两种情况。
①当隧道埋深H大于2.5hq时,荷载视为均布垂直压力,计算方法为
q=γHP=γ×2.5hq
(8)
即此时隧道的受力状态应按2.5hq的浅埋高度考虑竖向荷载。
②当隧道埋深H小于等于2.5hq时,荷载视为垂直均布压力,计算方法为
q=γH
(9)
即此时隧道的受力状态应按隧道埋深H的浅埋高度考虑竖向荷载。
综上所述,以上方法可为基坑隧道相邻近情况下的隧道结构竖向荷载的确定提供新的思路,供设计施工借鉴参考。
4.2 数值模型的建立
基于深埋隧道围岩压力的计算方法,本节将再加入3个压力拱影响因素:隧道埋深、隧道跨径、围岩等级。将这3个因素与前章节的3个因素结合起来,最终计算了216个模型,部分结果如表10所示,供设计施工单位参考借鉴。
4.3 工程实例
拟建项目为重庆市某骨科医院整体迁建项目,拟建项目由住院部、医技部、行政办公楼和地下车库组成。轨道交通9号线自东南向西北下穿拟建项目场地,整个拟建项目均位于轨道交通9号线50 m控制保护范围内,如图10所示。

图10 拟建项目及其与轨道交通平面关系Fig.10 The proposed project and its relationship with the rail transit plane
拟建项目施工后,新建的轨道9号线区间暗挖隧道竖向埋深约24.2 m,属于深埋隧道,隧道跨度为12.52 m,基坑开挖深度约为37.2 m,基坑距离区间隧道水平距离仅3.69 m,围岩等级近似于Ⅳ级围岩。而根据以上数据,由表10可得,符合隧道净跨B=10 m,隧道埋深H=25 m以及隧道净跨B=14 m,隧道埋深H=25 m,其上方围岩压力拱未成拱,即区间隧道应按浅埋隧道考虑。

表10 Ⅴ级围岩下既有基坑开挖对新建隧道影响下等效荷载高度值
h=0.45×2(4-1)×[1+0.1×(12.52-5)]=6.31 m;
HP=2.5hq=15.775 m<24.2 m。
因此区间隧道应按浅埋隧道考虑,最终此工程实际也按照浅埋进行设计计算。
5 结论
(1)针对内外边界值变化情况,阐述如下两点:①基坑深度和宽度超过某一临界值、基坑与隧道之间净距低于某一临界值,压力拱内边界才会增加,隧道上方松动围岩范围增加,围岩压力增加,隧道稳定性降低;②基坑深度和宽度越大、基坑与隧道之间净距越小,压力拱外边界增加值就越大,围岩稳定性降低,且当基坑深度处于近隧道埋深的某一临界范围值、基坑宽度超过某一临界值、净距小于某一临界值时,外边界会迅速增加到地表以上,围岩受埋深限制将无法形成安全有效的压力拱,深埋变浅埋,围岩压力突增,隧道稳定性降低。
(2)既有隧道上方围岩压力拱内外边界值受新建基坑三因素的影响情况与新建隧道受既有基坑三因素的影响情况基本相似。
(3)由于既有隧道受到支护结构的支撑,其压力拱内外边界受基坑三因素的影响敏感度要低于新建隧道,尤其是当基坑宽度增加时,既有隧道压力拱内边界保持不变,外边界无不成拱情况发生;其受基坑深度和净距两因素的影响敏感度略低于新建隧道。
(4)基于压力拱内边界的变化必然导致隧道结构竖向荷载的变化,从而确定受基坑影响下的隧道垂直均布压力计算方法。引入内边界增加值Δh,用于计算隧道在基坑影响下增加的竖向均布荷载,得到围岩压力突增后的隧道结构竖向荷载值。
(5)当隧道压力拱外边界受影响较大时,隧道由无基坑状态时的深埋状态变为浅埋状态,此时,隧道不能按深埋隧道只考虑坍落拱高度范围的竖向荷载,最不利的受力状态应按H的浅埋高度或埋深2.5hq的浅埋高度考虑竖向荷载。
(6)从不同围岩等级、隧道跨度和埋深,及不同基坑的深度、宽度及基坑与隧道的净距,共6个影响因素入手,组合排列,共建立216个数值模型,得出基于侧方基坑影响下的隧道竖向荷载等效高度取值,可供设计施工单位借鉴参考。

