基于改进突变理论的水库边坡稳定性风险分析——以前坪水库右坝肩边坡为例

张艺冰，刘汉东*， 杨继红， 李冬冬

(1.华北水利水电大学岩土工程与水工结构研究院,郑州 450046；2.河南省岩土力学与结构工程重点实验室, 郑州 450046；3.华北水利水电大学地球科学与工程学院，郑州 450046)

边坡失稳直接威胁人民生命财产和重大工程建设安全。边坡稳定性风险评价是边坡工程减灾防灾的有效途径，是岩土工程领域研究热点之一。

突变理论因其有助于解决复杂层次分析问题的优点，被广泛应用于边坡稳定性风险评价中。许多学者以突变理论为基础进行边坡综合评判[1-5]、稳定性分析[6-7]、风险分析[8]以及滑坡预测[9-12]。秦四清等[9]首先将突变理论引入边坡稳定性综合评判中。但是常规的突变评价法缺点十分明显，评价值过于集中，不利于风险程度的判别。因此很多学者对改进的突变评价法进行了研究[13-15]。唐明等[13]曾提出计算底层控制变量全部为{0, 0.1, 0.2,…, 1}时的顶层突变评价值，然后在每个等级刻度区间上利用线性关系调整突变评价值的改进方法。但由归一化公式可知，变量的取值和评价值之间并非线性关系，因此该方法并不严谨。李邵飞等[14]提出了构建突变综合评价值与底层指标隶属度值之间拟合函数关系式的改进方法，但此方法中所选函数特性与突变评价的特点不一致。突变评价法的改进核心问题在于选取一种与突变函数规律一致的方法，在此基础上将突变评价值的极差增加，更加客观地体现出评价结果的优劣性。

基于突变理论，将双曲函数引入突变评价法的改进工作中，旨在改善传统突变评价法评价值过于集中、评价结果过于接近的缺点。进一步将此应用于前坪水库右坝肩边坡稳定性分析中，结合三维激光扫描点云信息，探讨改进的突变评价法在边坡稳定分析中的应用，该方法能显著改善突变评价法的缺点，具有一定的创新意义，同时可为实际工程提供引导。

1 突变理论基本原理

突变理论于1968 年由法国数学家Thom提出，通过建立研究对象的势函数来研究外界控制参数的连续改变如何导致不连续现象的发生，即“突变”。突变理论主要由稳定的拓扑理论发展而来，并建立在拓扑动力学、奇点理论的基础之上，可用于研究多层次问题[16-17]。突变理论研究的是从一种稳定组态跃迁到另一种稳定组态的现象和规律，把系统状态变成不可微分，并用可数的控制参数表示变量，用变量的逐渐积累到状态改变表示突变过程，将无法描述的突变过程用函数方式表达出来，完成了科学的描述[18]。

运用突变理论评价法，并不需要确定各评价指标的权重。若评价体系中存在很多评价指标，可以考虑把各类指标划分为不同层次的评价指标体系。因此，可以将复杂种类繁多的指标体系进行简化，减少分析计算过程中的工作量，并且有助于较迅速地得出结果并加以利用。

利用以下两个公式将各指标值转换为0～1 的突变级数。

对于越大越优型指标：

(1)

对于越小越优型指标：

(2)

式中：X为初始指标值；Y为初始指标转换值；a1、a2为初始指标值的上、下界。

按照突变理论的分类定理，自然界中的大量不连续现象可由某些特定的几何形状来表示，表1所示为几种常见的初等突变类型[19]。

2 改进的突变理论评价法

突变理论评价法应用广泛，但针对其综合评价值差值不明显和优劣不显著的缺点改进的研究很少。

表1 几种常见的突变类型

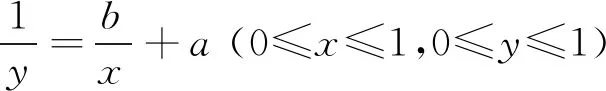
下面在显著性水平α=0.05下检验假设：

H0∶b=0,H1∶b≠0

采用相关系数法进行检验。n=18，n-2=16，查相关系数检验表，可得系数c=0.468，检验统计量的观测值

(3)

式(3)中：r为检验统计量的观测值；lx′y′为x与y的协方差；lx′x′为x的方差；ly′y′为y的方差。

|r|=0.539>0.468，所以拒绝H0，即认为y关于x的线性回归效果是显著的。具体改进的评价方法所得结果如表2[20]所示。

分析表2可以看出，用双曲函数改进后的突变评价结果极差增大，数据更加分散，分辨水平更高，评价结果的优劣更为明显。因此，将双曲函数拟合方法引入突变评价法的改进中是合理的。

表2 算例评价结果对比[20]

3 前坪水库右坝肩边坡稳定性风险分析

3.1 工程背景

前坪水库位于北汝河上游，河南省汝阳县城西9 km 处的前坪村。水库右坝肩高边坡基岩裸露，边坡最高达105 m(图1、图2)。边坡岩性主要为安山玢岩，岩体裂隙发育。根据三维激光扫描点云图(图3)得到，前坪右坝肩边坡共提取节理裂隙145条，图4所示为节理裂隙玫瑰花图。

图1 前坪水库右坝肩Fig.1 Right abutment of Qianping Reservoir

图2 削坡后的右坝肩Fig.2 Right abutment after cutting the slope

图3 前坪水库右坝肩激光扫描点云图Fig.3 Image of point cloud of right abutment of Qianping Reservoir

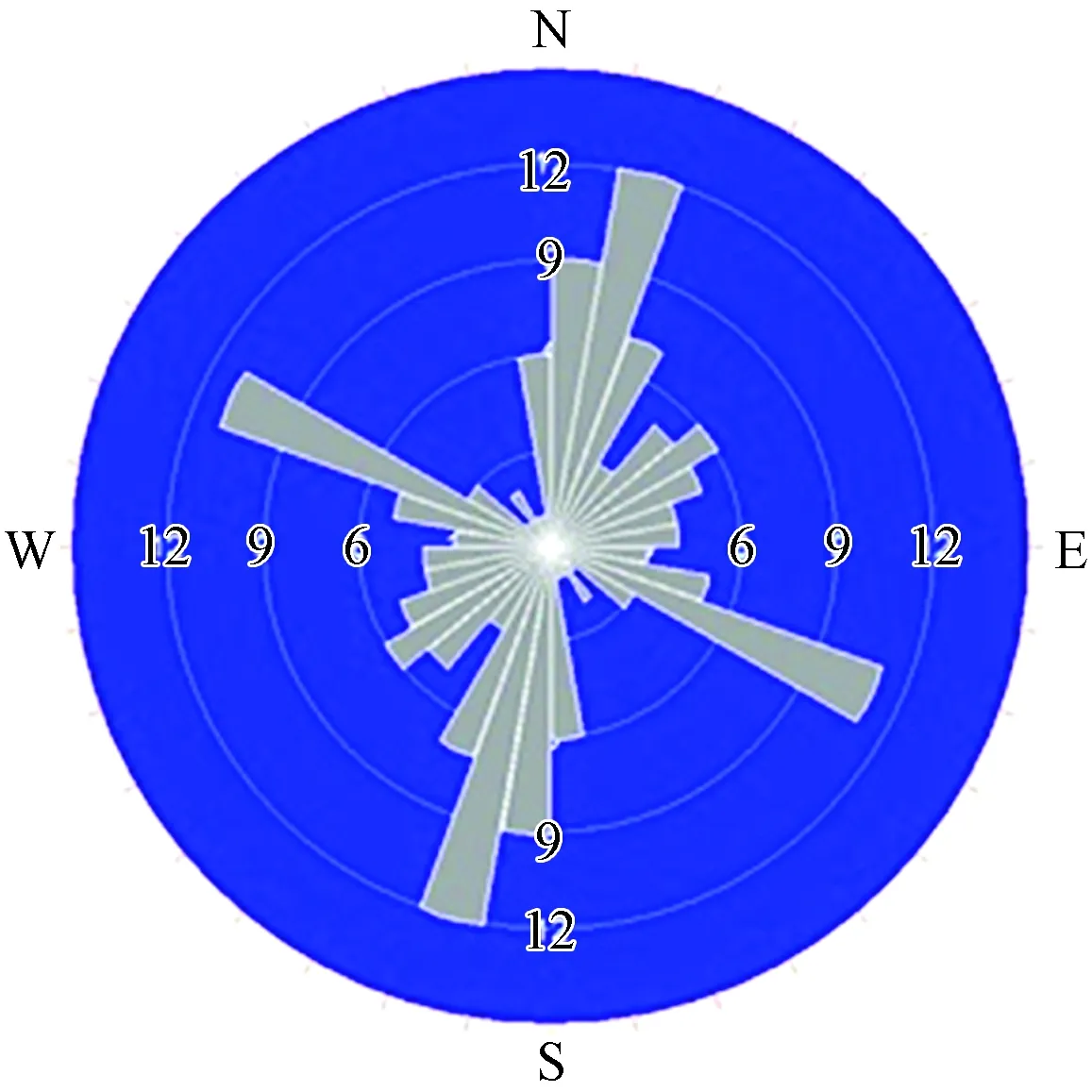
图4 节理裂隙玫瑰花图Fig.4 Rose flower picture of joints and cracks

3.2 评价指标体系的建立

前坪水库右坝肩边坡岩体为镶嵌碎裂结构，在空间分布上具有不连续性。依据坝址区工程地质条件，对边坡稳定性评价指标进行整理和筛选，将边坡风险评价目标分解为3个二级指标，进一步将3个二级指标分解为7个三级指标，建立前坪水库右坝肩边坡稳定性风险评价指标体系(图5)。

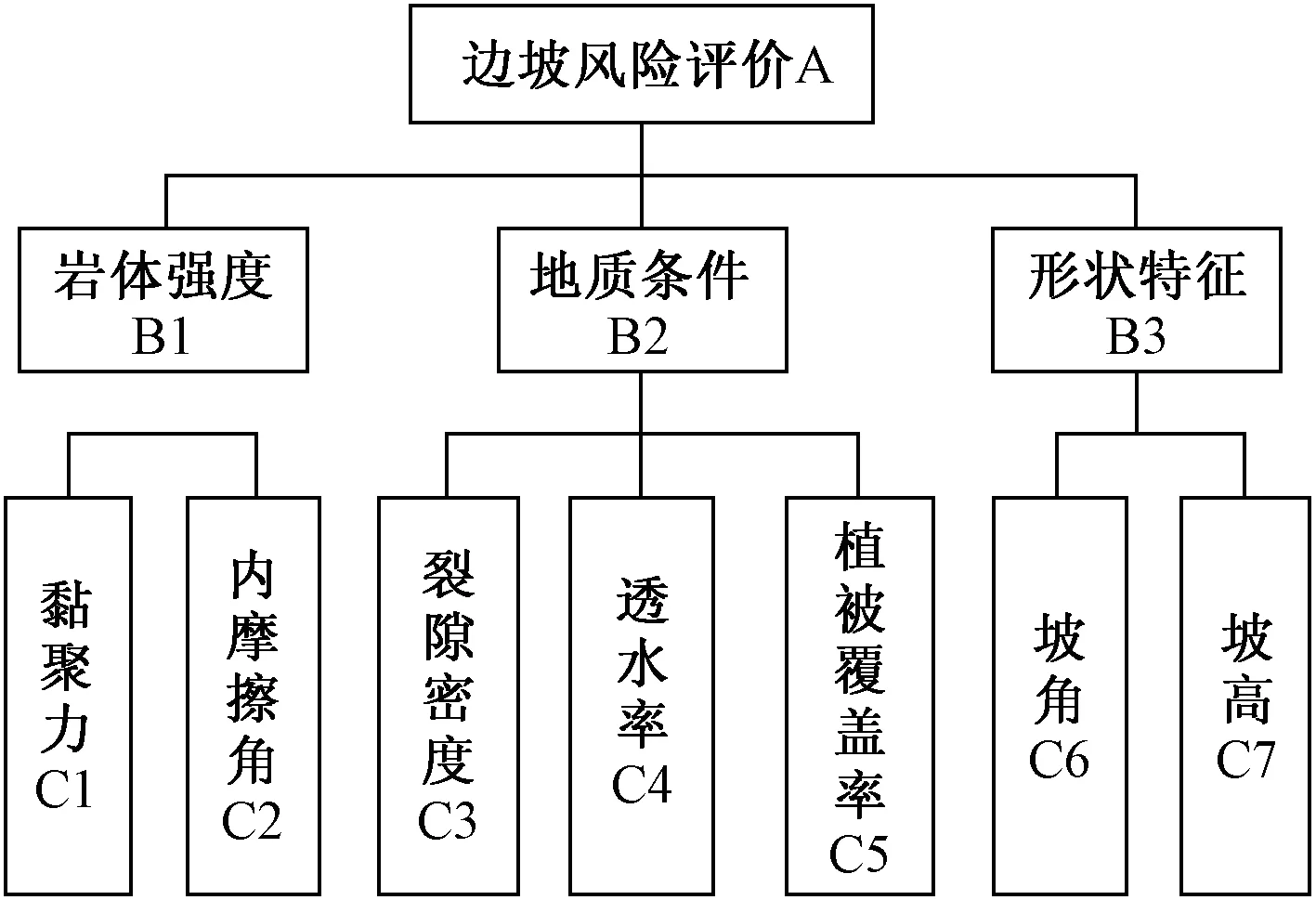
图5 前坪水库右坝肩边坡稳定性风险评价指标体系Fig.5 Risk evaluation index system for stability of right abutment slope of Qianping Reservoir

3.3 常规的突变评价值的计算

利用式(1)、式(2)，将各个三级指标值转换为 0～1 的突变级数(表3)。

表3 前坪水库右坝肩边坡风险评价指标转换值

根据常见突变函数类型可知，C1、C2构成尖点突变，C3、C4、C5构成燕尾突变，C6、C7构成尖点突变，B1、B2、B3构成燕尾突变。若控制变量间不存在明显的关联作用，取值遵循大中取小的“非互补”原则；反之遵循“互补”原则，取控制变量相应的突变级数值的平均值。计算步骤如下：

C1、C2指标符合互补原则，则采用取均值原则，即

xB1=0.524 2。

同理，C3、C4、C5符合非互补原则，采用“大中取小”原则，C6、C7符合互补原则。B1、B2、B3符合互补原则，取这3项均值求出A的值。计算结果如表4所示。

表4 常规突变评价法的计算结果

3.4 双曲函数参数的确定

基于常规突变评价法得出的底层指标初始转换值xi及所对应的突变评价值yi如表5所示。

表5 归一化后的xi、yi对应值

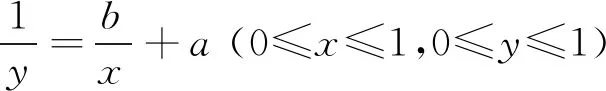
y′=bx′+a

(4)

利用极大似然估计法来估计a、b。

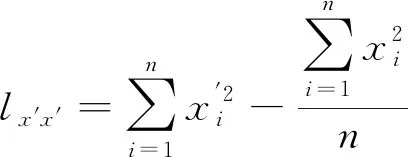
(5)

(6)

(7)

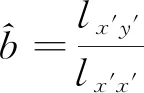
(8)

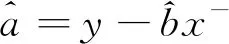
(9)

此处n=7。将表6中数据代入式(5)～式(9)中，求出a=1.373 2,b=0.036 4。

得出拟合函数如下：

(10)

在显著性水平α=0.05下检验假设：

H0∶b=0,H1∶b≠0

(11)

采用相关系数法进行检验。n=7，n-2=5，查相关系数检验表，可得此时c=0.754，r的观测值为

(12)

|r|=0.837>c=0.754，所以拒绝H0，即认为y关于x的线性回归效果是显著的。将数据代入式(10)，可得出拟合后的评价值。

3.5 对比分析

从表6评价结果对比分析，经双曲函数拟合后所得的改进突变评价值极差增大、分布变分散、优劣性更加明显，分辨水平更高，更符合一般情况下对优劣性的判断。从改进的突变评价值可以看出，A增大，形状特征风险值B3最大，且B3、B1明显大于B2，说明研究对象的形状特征风险最大，最值得关注。因此，为保证工程建设安全，在边坡工程施工建设阶段应重视边坡稳定性研究，应重视边坡形状设计问题。

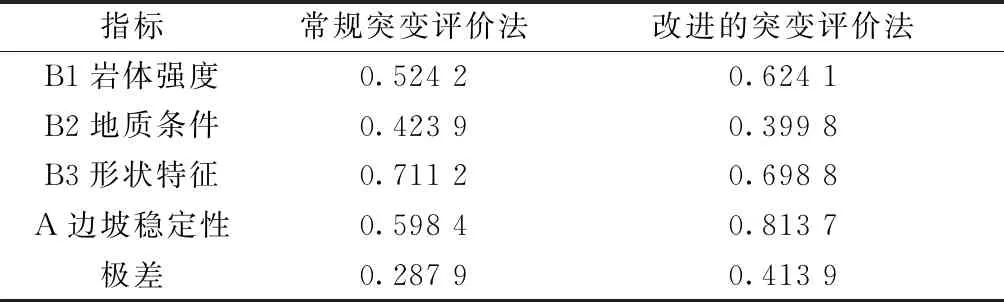
表6 改进的评价方法结果对比

4 结论

基于突变理论，通过构建双曲函数，对风险评价底层指标的初始转换值与突变评价值进行拟合，求得双曲函数参数后进行显著性检验，进而求出算例中改进后的突变评价值，验证了此方法的合理性，并将其应用于前坪水库右坝肩边坡风险评价运算中。通过评价结果对比分析，此方法得到的风险评价结果较常规的突变评价法具有更高的分辨水平，优劣性更为明显，对实际工程建设有一定的指导作用。