基于目标参数最优的磁耦合谐振式无线能量传输系统频率特性分析及仿真验证

范兴明，贾二炬，高琳琳，张伟杰，焦自权，张 鑫

(1. 桂林电子科技大学 机电工程学院, 广西 桂林 541004;2. 广州金升阳科技有限公司, 广州 510700)

由于电线的裸露、老化以及尖端放电等因素，传统的接触式输电会产生电火花，缩短设备的寿命.此外，接触式输电受到水下矿井和人体植入式等特殊场合的限制，用电设备的增多将会造成电线繁杂，影响线路布置和安全.而无线能量传输(Wireless Power Transfer，WPT)技术可以有效地弥补有线电能传输方式的弊端，具有更高的稳定性和可靠性，更加符合未来社会发展的趋势[1].目前，常用的WPT技术主要包括电磁感应式、磁耦合谐振式以及微波辐射式[2].与电磁感应式相比，磁耦合谐振式的传输距离更远；与微波辐射式相比，磁耦合谐振式的传输效率更高，因此表现出极大的应用潜力[3-7].

目前，国内外研究人员对磁耦合谐振式无线能量传输(Magnetically Coupled Resonant Wireless Power Transfer, MCR-WPT)技术进行了一系列的研究，并取得了一定的研究成果[8-15].文献[8-9]对比分析了该系统的耦合模理论和等效电路理论，得到两种理论模型具有等效性的条件.文献[10]从电路角度对MCR-WPT系统的最大传输效率进行分析，得到系统最大效率条件及最大效率表达式.文献[11]对盘式线圈的参数优化设计，解决了特定条件下的具体谐振器设计问题.文献[12]从感性、容性和纯阻性3个方面研究了系统的负载特性，提出电容补偿和电感补偿的方法可提高传输效率.文献[13]分析了含有中继线圈的系统特性，得到临界耦合条件和最大功率传输条件.文献[14]研究了系统的恒流补偿网络，证明电流增益与负载无关.目前多数文献针对系统的频率分裂现象[2,15-16]展开研究，指出距离和负载的变化会导致系统失谐，并提出了采用锁相环、扰动分析法及自动阻抗匹配法等调频策略可以提高系统的传输性能[17-20].尽管如此，导致系统失谐的具体影响因素有待深入研究，特别是在分析距离和负载的变化对系统最佳工作频率的影响时，已有研究大多忽略了频率对线圈内阻的影响，因此对分析结果趋势的正确性造成不利影响，进而影响系统频率控制策略的选择和控制的精确性.

本文对系统频率特性进行较全面的研究.利用阻抗反射理论研究负载和距离的变化对系统频率稳定性的影响.基于互感理论对串串型拓扑结构进行建模，从理想和非理想状态条件下分析距离和负载的变化对系统输出功率和传输效率的最佳频率的影响规律.利用MATLAB对WPT系统频率特性分析相关理论进行系统建模，采用插值法和多项式拟合对系统最佳效率工作频率进行求解和仿真验证.本文研究结果可为MCR-WPT系统频率特性分析提供理论和模型参考，并可进一步为MCR-WPT系统的精确频率控制策略提供一定的理论指导.

1 系统频率稳定性的影响分析

MCR-WPT系统常用的拓扑结构如图1所示，具体包括串联-串联补偿(SS)型，串联-并联补偿(SP)型，并联-串联补偿(PS)型和并联-并联补偿(PP)型4种[21].图中US为高频电源；L1、R1、L2、R2、C1、C2、I1以及I2分别为发射线圈和接收线圈的等效电感、等效电阻、谐振补偿电容和电流；M为两线圈间的互感；RL为接收端负载.

图1 MCR-WPT系统拓扑结构类型Fig.1 Topological structure types of MCR-WPT system

由于互感的存在，传输距离和负载的变化会对发射端的阻抗产生影响，导致发射端的等效电感发生变化，并可能导致系统失谐.接收端对发射端的影响可用反射阻抗Zr表示.将图1进行简化，得到发射端分别采用串联和并联补偿的等效阻抗电路模型，如图2所示[22].图2中Z1为发射线圈的阻抗，Z1=R1+jωL1，阻抗往往由复数形式表示， j为阻抗的复部，ω为角频率，ω=2πf，f为频率.

图2 发射端阻抗等效电路Fig.2 Equivalent circuit of impedance in sending terminal

(1)

MCR-WPT系统的关键特征是保持发射端和接收端同时共振，且线圈的自谐振频率与系统的驱动频率相同.通常假设接收端共振，研究距离或负载的变化对发射端等效阻抗的影响.系统共振时发射端需满足的条件为：发射端阻抗ZP或导纳Yt的虚部为0.在分析此问题时，目前多数研究忽略了线圈内阻的影响，将导致在计算谐振补偿电容时出现偏差，进而降低了系统的实用性能.表1给出了4种不同电路拓扑结构情况下考虑线圈内阻的影响时负载或距离的变化对发射端谐振补偿电容的影响，其中，RS为线圈内阻，ω0为考虑线圈内阻的影响时的角频率.

由表1可知，在SS型拓扑结构中，传输距离或纯阻性负载的变化不会导致C1发生变化；在SP型拓扑结构中，传输距离的变化会导致M变化，进而对C1的数值产生影响，纯阻性负载的变化对发射端没有影响.在PS和PP型拓扑结构中传输距离和纯阻性负载的变化均会改变C1，并可能造成系统失谐.由此可得出结论：当发射端采用并联补偿时，传输距离或负载的变化都会造成系统的失谐.当采用SS型补偿时，系统频率的稳定性最好；当采用SP型补偿时，系统的工作频率不受纯负载变化的影响.

表1 不同拓扑结构下的系统参数Tab.1 System parameters in different topological structures

注：∥为并联符号.

2 系统理论模型的建立

图3 MCR-WPT系统等效电路模型Fig.3 Equivalent circuit model of MCR-WPT system

由于SS型拓扑结构的发射端和接收端相互独立，接收端负载和传输距离的变化不会导致系统失谐，因此文下重点研究SS型拓扑结构及其特征.基于SS型拓扑结构的MCR-WPT系统等效电路模型如图3所示.图中D为两线圈间的距离；IP和IS分别为发射与接收回路的电流.

根据基尔霍夫电压定律，电路方程为

(4)

对式(4)进行求解可得IP和IS，进而可得到系统的输入功率PS、输出功率P与传输效率η的计算表达式[10]：

(5)

(6)

(7)

3 系统最佳工作频率的分析

3.1 理想状态下系统最佳工作频率的影响分析

理想状态下，发射端与接收端均发生共振，ZP与ZS的虚部为0.系统的输出功率和传输效率的计算表达式为[11]

(8)

(9)

3.1.1理想状态下系统输出功率最佳频率的确定 通常，由于线圈的内阻较小，研究者忽略频率的变化对线圈内阻的影响.此时，对式(6)关于ω求一阶导数并令其导函数的值为0，从而得到理想状态下不考虑频率对线圈内阻的影响时，系统的输出功率最佳频率：

(10)

然而，忽略线圈内阻会影响系统最佳工作频率的精确性，尤其在实现控制策略时，参数的准确性对控制的精确性起决定性作用.在高频状态下，线圈的等效电阻主要包括欧姆电阻和辐射电阻，其中，欧姆电阻的影响更为明显[23].所以，本文重点研究线圈欧姆损耗对系统工作频率的影响.欧姆损耗的计算公式为[11]

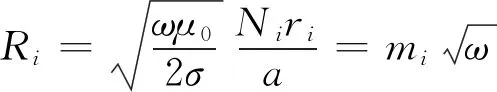
(11)

式中：μ0为真空中的磁导率；σ为导线材料的电导率；Ni为第i个线圈的匝数；ri为第i个线圈的平均半径；a为线圈的导线半径；mi为拟合参数，

考虑频率对线圈内阻的影响时，对式(8)求关于ω的偏导数并令其导函数的值为0，可以得到理想状态下考虑频率对线圈电阻的影响时，系统的输出功率最佳频率：

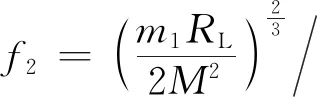
(12)

两线圈间互感为[11]

(13)

3.1.2理想状态下系统传输效率最佳频率的影响 在理想状态下，发射端和接收端同时谐振，且该谐振频率与系统的工作频率相同.当忽略工作频率对线圈电阻的影响时，对式(9)求ω的一阶导数：

(14)

式(14)中等号右端恒大于0，因此传输效率随着工作频率的增加单调递增.当考虑工作频率对线圈电阻的影响时，对式(9)关于ω求一阶求导并令其导函数的值为0，可得理想状态下考虑频率对线圈内阻的影响时，系统传输效率最佳工作频率满足：

3RL+m1m2ω+

(15)

在高频时，ω的数量级为106，因此式(15)难以进行求解，为了简化分析，文献[24]只考虑ω2项，得到传输效率最佳工作频率：

(16)

比较式(14)和(16)可知，传输效率随着频率的增加呈非线性变化，存在最佳工作频率点使系统达到最大传输效率.传输效率最佳工作频率与负载近似成正比，与距离的3次方成反比.这说明在分析系统的传输效率最佳工作频率时不能忽略频率对线圈内阻的影响.可以在已知系统参数的条件下采用插值法、曲线拟合法等求式(15)的相对精确解.

3.2 非理想状态下系统最佳工作频率的影响分析

在非理想状态下，发射端和接收端不同时谐振，且频率未必与系统的工作频率相同[15].此时，PS、P以及η的计算表达式为

(17)

(18)

(19)

3.2.1非理想状态下系统输出功率最佳频率的影响 为了便于分析，假设发射和接收线圈的参数完全相同(L1=L2=L，C1=C2=C，R1=R2=R).在非理想状态下，发射端和接收端阻抗的虚部相同(X1=X2=X)，定义广义失谐因子ξ，ξ=X/R，引入负载系数KL,KL=RL/R，可得ZP和ZS的计算表达式为

(20)

定义耦合强度KC,KC=ωM/R，则负载两端的电压为

(21)

求UL的模并对其进行归一化处理可得系统的输出电压增益：

(22)

(23)

ω=ω0时，发射端和接收端同时共振，此时称系统工作在“全谐振”状态；ω=ω2,3时，发射端和接收端均不共振，但系统整体工作在谐振状态，称为“部分谐振”状态.假设系统工作在分裂的ω2,3处，即系统处于“部分谐振”状态，此时系统的传输效率为

(24)

结合式(24)和(9)可得系统频率为分裂的角频率时传输效率与系统工作在全谐振状态下的传输效率的比值ε：

(25)

满足KL≫1且KC≫KL，即满足式(26)时，ε的值无限趋近于1，即系统频率为分裂的角频率时传输效率与系统工作在全谐振状态下的传输效率基本相等，且传输效率接近1:

R≪RL≪ZPS

(26)

式中：ZPS=ω2M2/R，可理解为初级回路对次级回路的反射阻抗.由此可得出结论：在满足式(26)的情况下，将系统的工作频率调整到分裂频率，在几乎不降低系统传输效率的情况下可有效地提高系统的输出功率.

3.2.2非理想状态下系统传输效率最佳频率的影响 对式(19)进行变形可得

(27)

为了便于分析，同样假设发射线圈和接收线圈的参数完全相同，记式(27)的分母为f(ω).结合式(11)，计算f(ω)关于ω的偏导数可得

(28)

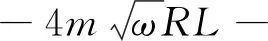
对σ求关于ω的偏导数可得

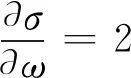
(29)

经计算，m的值的数量级为10-4，为了便于分析，忽略m的影响，由此可判断式(29)的右端恒大于0.由此可知，σ随着ω的增加单调递增，当ω趋于0时，σ趋于负无穷大；在ω趋于正无穷大时，σ趋于正无穷大，有且只有一个根使σ的值为0.因此可断定，在整个工作频率范围内，f(ω)随着ω的增加在一定区间内先单调递减，后单调递增.η随着ω的增加呈现出先增加后减小的趋势，有且只有一个工作频率使系统的传输效率达到最大，这也说明了非理想状态下系统的传输效率不存在频率分裂现象[15].

4 仿真分析与验证

为了证明理论分析的正确性，采用MATLAB对系统进行仿真验证.仿真时系统的工作条件为：US=50 V,f=13.56 MHz,D=0.5 m,P=80 W,RL=605 Ω.线圈参数为：线圈最大外径Dmax=0.439 5 m，线圈最小内径Dmin=0.360 5，线圈匝数N=8，填充率β=0.098 75，线圈匝间距S=3 mm，线圈线径W=2 mm.

4.1 理想状态下系统最佳工作频率的仿真分析

系统在理想状态工作时，在忽略和考虑频率对线圈内阻影响的情况下，改变系统的工作负载或传输距离，分别计算系统的输出功率最佳频率(记为理论值1，理论值2)，并利用MTALAB进行仿真，结果如图4所示.由图4可知，理论值1与仿真值的偏差较大；理论值2与仿真值有较好的吻合性.说明距离或负载发生变化时，考虑频率对线圈内阻的影响能够比较准确地反映系统频率的实际变化规律.

针对忽略和考虑频率对线圈内阻影响两种情况，利用MATLAB建立分析模型得到系统的传输效率与工作频率的关系(记为仿真值1，仿真值2)，如图5所示.

图5 传输效率与工作频率关系图Fig.5 Transmission efficiency as a function of working frequency

仿真值1随着频率的增加而增加，仿真值2随着频率的增加呈现出先增加后减小的趋势，即存在最佳工作频率使系统的传输效率达到最大.因此在分析传输效率最佳频率时不能忽略频率对线圈内阻的影响.

4.2 非理想状态下系统最佳工作频率的仿真分析

4.2.1输出功率最佳频率仿真分析 非理想状态下，为了验证距离和负载的变化对系统输出功率最佳频率的影响，先假定RL=605 Ω固定不变，改变系统的传输距离，得到系统电压增益与传输距离和工作频率的关系，如图6所示.由仿真结果可得系统发生频率分裂的临界距离为0.28 m.由图6可知，当D>0.28 m时，输出电压增益的最大值始终保持在系统的中心工作频率13.56 MHz处.当D<0.28 m时，输出电压增益由单峰变成了双峰，在中心工作频率处系统的电压增益变为局部最小值.

图6 输出电压增益与工作频率和传输距离的关系Fig.6 Output voltage gain as a function of working frequency and transmission distance

假定D=0.5 m固定不变，改变系统的工作负载，得到电压增益与系统的工作负载和频率的关系，如图7所示.

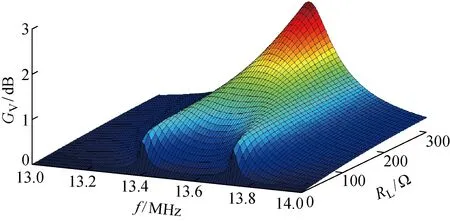
图7 输出电压增益与工作频率和负载电阻的关系Fig.7 Output voltage gain as a function of working frequency and load resistance

由仿真结果可得系统发生频率分裂的临界负载为154 Ω.当RL>154 Ω时，输出电压增益的最大值始终保持在系统的中心工作频率13.56 MHz处.当RL<154 Ω时，输出电压增益由单峰变为双峰，在中心工作频率处电压增益由最大值变为局部最小值.

为了分析距离和负载的变化对分裂频率的影响，分别固定RL=605 Ω，D=0.5 m，得到分裂频率与距离或负载的变化关系，如图8所示.由图8可知，距离和负载越小，系统频率分裂越严重.其中工作频率低于13.56 MHz的模式被称为“偶模式”，高于13.56 MHz的模式被称为“奇模式”.传输距离或负载越小，系统的频率分裂现象越严重，偏离中心频率越多.比较图8的纵坐标可知，距离对分裂频率的影响更为明显.

图8 分裂的频率与传输距离和负载的关系Fig.8 Splitting frequency as a function of transmission distance and load

由此可得出结论：传输距离或负载过小时，系统均会发生频率分裂现象，且传输距离和负载越小，系统的频率分裂越严重.在偏离中心工作频率下，系统的输出电压增益下降越大，输出功率越低.

图9 工作在分裂频率和中心谐振频率时的传输效率比较Fig.9 Comparation of transmission efficiency between split frequency and central resonance frequency

为了对比分析系统工作在分裂频率和中心谐振频率时的传输效率，分别改变系统的传输距离和负载，得到系统工作在偶模式、奇模式与全谐振3种模式下的传输效率与距离和负载的变化关系，如图9所示.为了能够更好地对比说明图9中传输效率的变化规律，根据式(26)将3种模式下距离和负载变化时比较阻抗值R、RL及ω2M2/R的变化情况列出，分别如表2和3所示.

图9(a)中，偶模式、奇模式与全谐振模式下的传输效率基本上都保持一致，且接近100%，与文献[16]得出的“过耦合时传输效率变化不大”的实验结果相一致.这是因为D在0.1～0.3 m变化时，表4中的数据满足式(26)，从而使系统的效率接近100%且基本保持不变.

图9(b)中，RL在0～20 Ω时，系统工作在全谐振模式下的传输效率高于工作在偶模式和奇模式下的效率，且效率较低.RL在50～200 Ω时，3种模式下的传输效率基本上相等，接近100%.这是因为RL在0～20 Ω时，表3中的数据ω2M2/R≫R成立，但RL≫R不成立，致使系统效率偏低；RL在50～200 Ω时，表3中的数据满足式(26)，曲线变化规律与理论分析一致，由此证明了式(26)的正确性.

表2 距离变化时阻抗与工作模式的关系

Tab.2 Impedance as a function of working modes with distance’s variation

工作模式比较阻抗/ΩRRLω2M2/R偶模式1.493～1.637605(1.194～0.122)×106奇模式1.993～1.682605(1.804～0.178)×106全谐振模式1.656605(1.433～0.082)×106

表3 负载变化时阻抗与工作模式的关系

Tab.3 Impedance as a function of working modes with load’s variation

工作模式比较阻抗/ΩRRLω2M2/R偶模式1.640～1.6520～200(7.235～7.320)×103奇模式1.672～1.6600～200(7.459～7.373)×103全谐振模式1.6560～2007.345×103

当系统发生频率分裂时，系统工作在全谐振模式下的输出功率较低，而奇模式下系统的工作频率较高，辐射损耗较大，导致系统传输效率低于偶模式[19].因此当系统发生频率分裂时，通过调频策略将系统偶模式下的工作频率调整到ISM(Industrial Scientific Medical)频段[20]，能够在基本上保持传输效率不变的条件下有效地提高系统的输出功率.

4.2.2传输效率最佳工作频率仿真分析 利用MATLAB对系统的传输效率进行仿真分析，结果如图10和11所示.可以看出：无论距离还是负载发生变化，只有在f=13.56 MHz时，系统的传输效率达到最大，即距离和负载的变化对系统传输效率最佳工作频率没有影响.此外，从图10和11中还可以看出，D和RL在较小和较大的范围内变化时，系统的最大效率工作频率始终保持在接收端的共振频率处，不随距离和负载的变化而发生变化，系统的传输效率不会发生频率分裂现象，与理论分析的结果一致.

图10 传输效率与工作频率和传输距离的关系Fig.10 Transmission efficiency as a function of working frequency and transmission distance

图11 传输效率与工作频率和系统负载的关系Fig.11 Transmission efficiency as a function of working frequency and system load

4.3 传输效率最佳工作频率的仿真计算

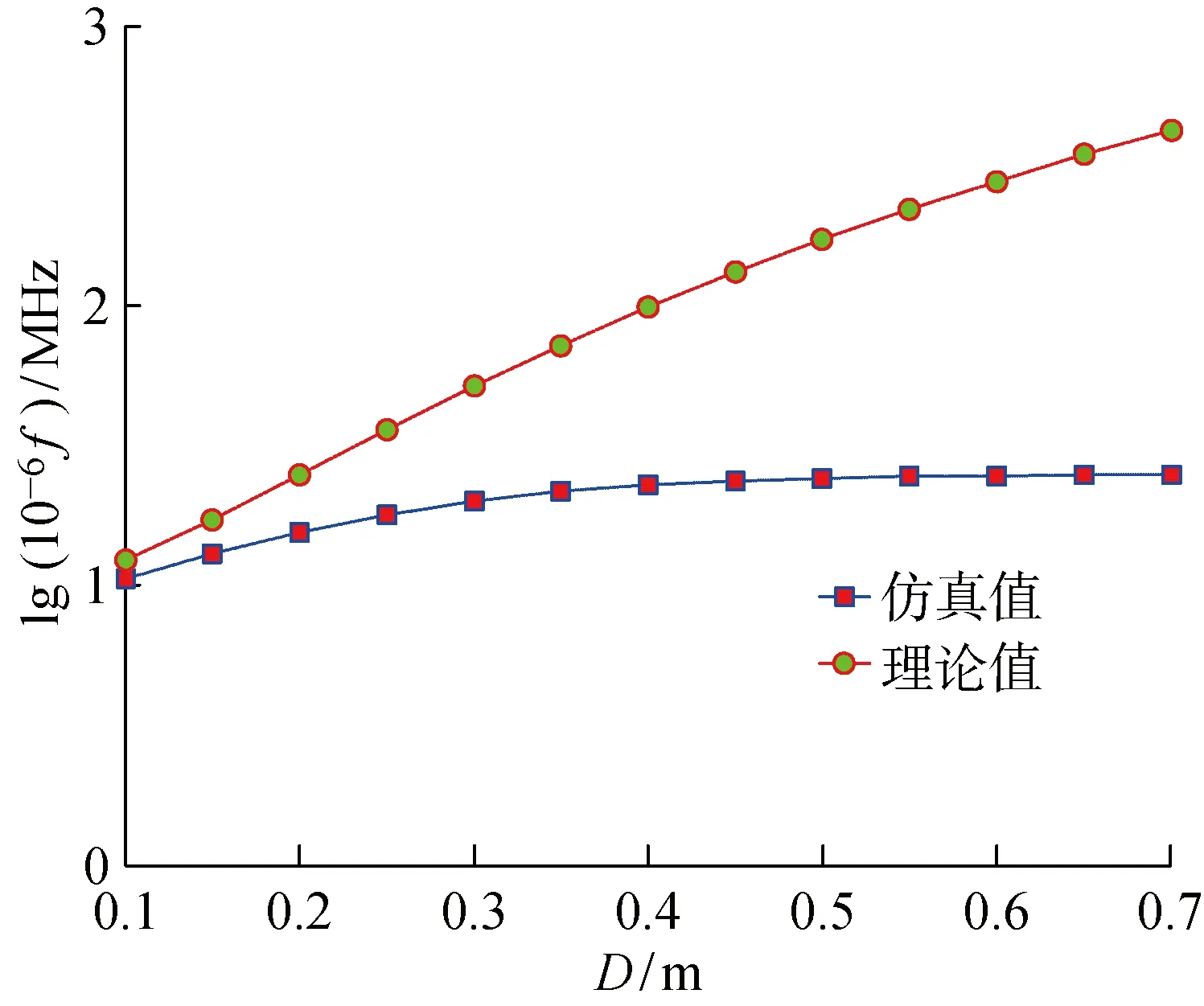
图12 最大效率工作频率理论值与仿真值比较Fig.12 Comparison of maximum efficiency working frequency between theory and simulation values

图13 最大效率工作频率值2～4次多项式拟合验证Fig.13 Verification of maximum efficiency working frequency value by 2-4 polynomial fitting

由图13可知，拟合曲线的变化趋势与仿真结果有较好的吻合性，但是仍存在偏差.为此增加拟合次数并采用插值法对式(15)进行求解，结果分别如图14和15所示，图中er为频率相对误差.

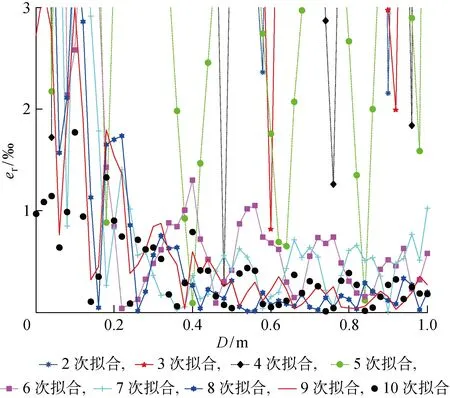
图14 拟合次数与频率相对误差的关系Fig.14 Relative frequency error as a function of polynomial fitting times

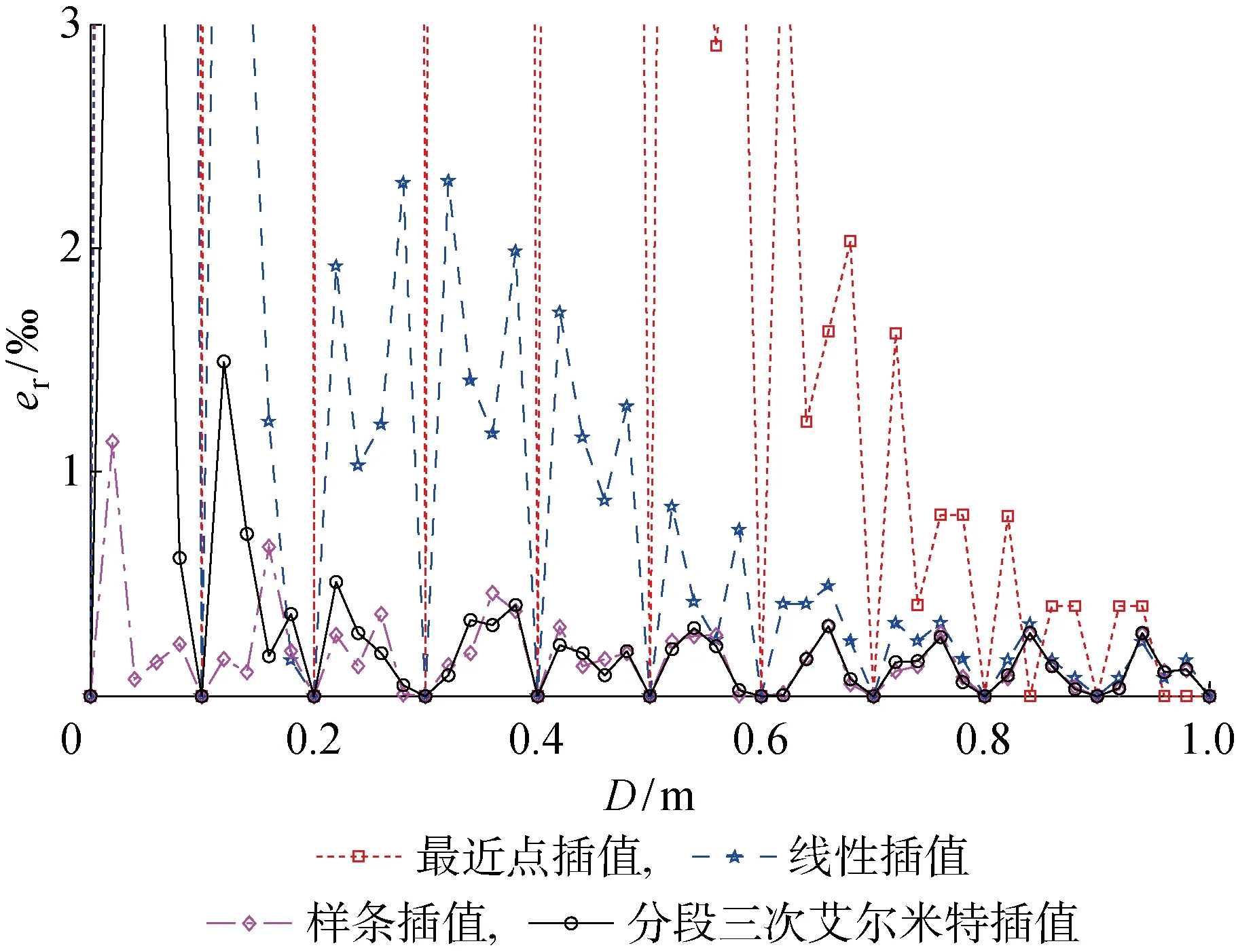
图15 不同的函数插值法与频率相对误差间的关系Fig.15 Relative frequency error as a function of different interpolation methods

在图14和15中，为了能够清晰地反映出误差的大小，限定纵坐标的取值范围是[0, 3‰].由图14可知，当选用8次拟合时，拟合的仿真结果偏差最小.由图15可知，样条插值法的频率相对误差较小.在实际计算中，可以在已知系统参数的条件下，采用样条插值法或者是8次曲线拟合来得到式(15)的相对精确解.

5 结论

在MCR-WPT系统中，系统工作频率的变化会对系统的传输性能产生较大的影响.分析了4种拓扑结构下距离和负载的变化对系统共振频率的影响，表明串串型拓扑结构的稳定性最好.利用互感理论研究了系统工作在在理想状态和非理想状态下的最佳工作频率，得出以下结论：

(1) 在分析最佳效率工作频率时不能忽略频率对线圈内阻的影响，考虑频率对线圈内阻的影响能够有效地提高分析的准确性;

(2) 在满足一定的条件下，可以利用系统的频率分裂现象在几乎不降低系统传输效率的情况下，有效地提高系统的输出功率;

(3) MCR-WPT系统中只有当接收端共振时，系统传输效率才最大，与发射端是否共振无关;

(4) 频率分裂只发生在系统的功率特性中，系统的效率特性并不存在频率分裂;

(5) 利用插值法和多项式拟合对理想状态下的最佳效率工作频率进行探索求解，仿真分析结果表明：样条插值法和8次多项式拟合方法能够比较精确地反映系统传输效率的最佳工作频率.