基于模糊迭代算法的曲面恒力跟踪

张 铁，肖 蒙，邹焱飚，肖佳栋

(华南理工大学 机械与汽车工程学院， 广州 510640)

机器人与环境接触过程中，通过力控制能够调节机器人与环境接触状态，从而达到理想的接触效果，因此力控制广泛运用于机器人打磨[1]、抛光[2]及曲面跟踪等.利用机器人跟踪未知曲面时，保持恒定的接触力能够得到精确的曲面轮廓.然而，在接触过程中，由于机器人自身属性[3](如机器人动力学特性，机器人刚度[4]以及未知环境是时变的(如曲面轮廓变化)，造成了机器人与曲面的接触力不稳定，波动较大，从而导致采集的曲面轮廓不够精确.

机器人恒力跟踪的研究大致可以分为传统控制(包括阻抗控制，力/位混合控制，自适应控制)和智能控制.传统控制方法中，吴得祖[5]利用六维力传感器对并联机器人和曲面接触点的刚度进行了测量，通过刚度控制对曲面进行恒力跟踪.Winkler等[6]在力/位混合控制中加入额外的积分器来减少静态控制误差，同时通过改变机器人速度来达到跟踪力恒定.智能控制中，Ye等[7]提出一种自适应模糊控制算法，在线对机器人的参数进行模糊补偿以适应环境的变化，自适应模糊控制器具有良好的鲁棒性.Jung等[8]在阻抗控制中加入了神经网络补偿，消除了不确定性的因素，包括环境中不确定性因素(如位置，刚度)以及机器人运动学中参数的变化造成的干扰.在三连杆机器人进行的仿真研究中，神经网络补偿的力控制器使得机器人能够在未知环境中保持恒定的力，表现出良好的力跟踪性能.Wang等[9]利用模糊神经网络估计机器人在未知环境中所处的状态，在不同状态下通过调节不同的力控制参数来适应环境的变化，达到保持恒定力的状态，最后通过两自由度的连杆仿真验证了算法的可行性.王磊等[10]通过模糊推理智能地预测阻抗控制模型中的参考轨迹，并根据力误差变化调节参考比例因子，以适应未知环境刚度的变化，仿真结果证明了算法的有效性.

目前的研究中，传统控制算法很难补偿机器人跟踪过程中的各种不确定性，如机器人运动学的不确定性[11]，机器人末端传感器姿态的改变造成传感器示数的变化，而智能控制算法设计比较复杂，大多停留在仿真阶段.本文在力/位混合控制的基础上针对力控部分提出一种模糊迭代的智能算法，在机器人内部传递函数未知和机器人末端传感器姿态不改变的情况下，利用模糊算法补偿轨迹的误差，离线迭代更新机器人的轨迹，多次实验后，使得接触力在阈值范围内波动，最终得到比较稳定的跟踪力和较为精确轨迹.相比于传统的比例积分(PD)控制和迭代算法，模糊迭代算法能够得到更加稳定的跟踪效果和轨迹.

1 曲面跟踪运动受力分析

机器人恒力跟踪实验平台如图1所示，工作台坐标系S，传感器坐标系T和机器人基坐标系B的映射关系可以通过齐次变换矩阵来描述：

(1)

图1 机器人恒力跟踪实验平台Fig.1 Robot constant force tracking experimental platform

传感器安装在机器人末端，机器人通过安装在传感器上的探头与环境接触，如图2所示，在跟踪实验中，机器人保持vs的速度沿着xV方向运动，机器人运动坐标系V和传感器坐标系T的姿态始终相同.当探头与曲面接触时，探头受到曲面的法向力Fn和切向力Fτ，恒定的Fn能够反应出曲线的轮廓，为了得到Fn的大小，需要将曲面坐标系C中的力映射到已知的传感器坐标系T中，曲面坐标系C中心与传感器坐标系T中心重合，x轴方向与曲面的切向方向相同，y轴方向始终垂直于曲面轮廓，由图3中受力分析可知:

(2)

图2 机器人末端局部图Fig.2 Partial view of the robot end-effector

图3 机器人末端受力分析图Fig.3 Force analysis at the robot end-effector

式中：TFx和TFy分别为T坐标系下Fx和Fy；θ为xT与xC之间的夹角.将式(2)解耦可得:

(3)

TFx和TFy的大小可通过六维力传感器测得.θ在T坐标系下等于曲面切线倾斜角，因此需要对θ进行估计.在传感器T坐标系中，当机器人沿着xV方向和yV方向移动时，根据xV方向和yV方向上位移的差分可以得到每一小段的切线倾斜角为

(4)

2 模糊迭代算法

迭代学习控制适合于具有重复运行特性的被控对象[12]，由于迭代算法在无需系统的传递函数[13]的情况下，根据误差多次迭代就能达到所需要的状态，所以大大降低了机器人控制算法设计的难度.

机器人跟踪过程是离散的系统[14]，当机器人与环境刚性接触时[15]，通过改变机器人与环境的接触位移就能改变接触力的大小，因此通过迭代机器人轨迹上单独一段时间的偏移量可以修正机器人与环境的接触力.在迭代的过程中，通过学习前期迭代的效果调整迭代策略，加快收敛，直到达到预期的轨迹，假设机器人和环境接触时的状态方程为

(5)

式中：A(t)为动态特征矩阵；B(t)为控制矩阵；C(t)为输出矩阵；x(t) 为状态变量；u(t)为输入；y(t)为输出力.可以将迭代算法设计为

(6)

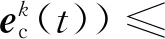
(7)

因此式(6)迭代算法范围为

(8)

(2) 每一次迭代的初始条件一致，即

其中：x0为初始状态；yd为初始期望输出值.则算法单调收敛[16]，当k→∞时有：

yk(t)→yd(t), ∀t∈[0,T]

(9)

式中：τ，δ为0～t之间的变量.取Φ(t，τ)=exp[A(t-τ)]，则：

xk+1(t)-xk(t)=

(10)

由于ek(t)=yd(t)-yk(t)，ek+1(t)=yd(t)-yk+1(t)，则：

ek+1(t)-ek(t)=yk(t)-yk+1(t)=

C(t)[xk(t)-xk+1(t)]=

(11)

对式(11)整理可知，

ek+1(t)=ek(t)-

(12)

将式(8)的输入代入式(12)，则第k+1次误差为

ek+1(t)=ek(t)-

Γ(τ)eck(τ)]dτ

(13)

令G(t,τ)=C(t)Φ(t,τ)B(τ)Γ(τ)，有：

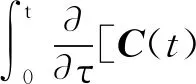
(14)

式(13)两边取范数：

‖ek+1(t)‖≤‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

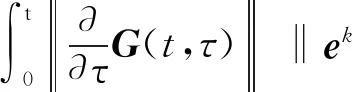
‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

(15)

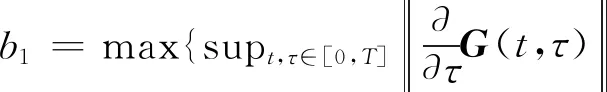
supt，τ∈[0，T]‖C(t)Φ(t，τ)B(τ)L(τ)‖}

其中T为迭代总时间.

定义1向量函数h:[0T]→Rn的λ-范数为

‖h‖λ=sup{exp(-λt)‖h(t)‖}(λ>0)

将式(15)两端同时乘以exp(-λt)，则有：

exp(-λt)‖ek+1(t)‖≤

exp(-λt)‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

(16)

其中：

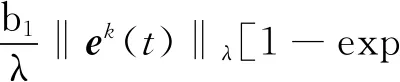
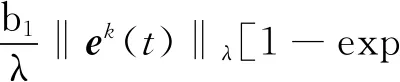
(17)

把式(17)代入式(16)中，则有：

exp(-λt)‖ek+1(t)‖≤

exp(-λt)‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

(18)

根据定义1可将式(18)化简为

‖ek+1(t)‖λ≤‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖λ+

(19)

(20)

式中：

图4 力控制算法Fig.4 Force control algorithm

图5 模糊算法流程图Fig.5 Flow diagram of fuzzy algorithm

输入变量和输出变量的基本论域分别取：

(21)

隶属度函数选择三角形函数，在解模糊过程中，选用重心法，即

(22)

式中：w0为解模糊得到的输出值；x为在论域v中的值；μN(x)为模糊集合N下对应x的隶属度函数值.模糊规则选用：

3 曲面轮廓恒力跟踪实验与分析

实验采用安川机器人MH24，机器人在运动中控制器内置软件MotoPlus接受外部 -10～10 V的模拟信号产生偏移，偏移位移方向与模拟信号符号一致，偏移位移与电压绝对值大小成正比；六维力传感器选用德国的ME-FKD40，由于传感器末端安装了探头，因此采集六维力信号后，需要通过转化矩阵得到沿着xT和yT方向的力，并对力的值进行标定，标定方法见文献 [18]；采集的力信号通过上位机处理发送给倍福模块，倍福模块产生电压模拟信号传送给机器人控制器；曲面工件的尺寸如图6所示，曲面的轮廓通过三维软件中样条曲线拉伸而成；曲面半径R为34 mm，机器人运动的初始点为A，终点为B，机器人始终以1 mm/s的速度沿着xV方向移动；期望的力Fd为30 N.

图6 曲面工件(mm)Fig.6 Curved-surface workpiece (mm)

图7 实验流程图Fig.7 Flow diagram of experiment

跟踪实验流程如图7所示，在实验过程中，机器人在运动过程中有以下几种干扰：传感器自身示数漂移干扰，底层算法插值运算处理时造成微小的丢步，运动过程中不确定性造成的干扰及摩擦力的干扰.为了避免干扰影响到整体的迭代效果，在迭代过程中每次改变力的大小不宜过大，迭代过程由前往后依次迭代.当实际接触力F与期望力Fd之差ΔFe符号不同时，机器人偏移量方向是相反的，由于机器人的重复精度不高，同样的迭代值下，每一次采集力的值一般会有较小的偏差，当ΔFe较小时，这种偏差会在重复实验时迭代更新相同进给量却造成相反的效果，加大误差，故迭代过程只针对于 |ΔFe|>3 N 的时间段，设定每次迭代实验力的阈值为10 N.

初始实验PD参数中比例参数P=0.03，微分参数D=0.5，式(6)的kr(t)=3.2，kp(t)=3，kd(t)=1，采样频率为 1 000 Hz，检测力信号中|ΔFe|>3 N的时间段，在超出阈值的时间段内，ΔFe的波形分为两种情况，一种情况为力信号没有回落，力信号一直增大或减小，为类型 I；另一种情况为力信号有回落，类似于抛物线，为类型 II.在迭代过程中，机器人在t时刻的总进给量等于t时刻进给量加上t时刻前进给量的总和，在更新当前时间段的偏移量时，为了保证后面时间段的偏移量不变，需要在后一段补偿这段改变的值，因此对有回落过程的迭代更新方程为

(23)

式中：ts为迭代开始时间；tp为ts到te时间段ΔFe绝对值的最大值对应的时间；te为迭代结束时间.迭代终止条件为：|ΔFe|<3 N.没有回落过程时只更新不补偿，迭代更新方程为

uk+1(t)=uk(t)+kp(t)ek(t)+

(24)

图8 倾斜角对比图Fig.8 Dip angle comparison chart

图9 接触力对比图Fig.9 Comparison chart of contact force

图10 轨迹对比图Fig.10 Trajectory comparison chart

实验选取4段信号对模糊迭代算法和未进行模糊补偿的迭代算法进行对比.未进行模糊补偿的迭代次数分别为4，3，5，4次， 模糊迭代算法的迭代次数分别为2，2，3，3次.分别选取类型I和类型 II 两种信号，对迭代过程进行对比，如图11～14所示，在未进行模糊补偿的迭代算法中每次迭代过程中根据力的大小选择迭代量， 经过多次实验后， 最终接触力在目标范围内，而在模糊迭代算法中，从第2次迭代开始利用前面实验中迭代误差补偿后续实验，加速收敛，如图12和14所示.

表1 模糊迭代算法和PD算法对比

Tab.1 Comparison between fuzzy iterative algorithm and PD algorithm

算法|e|max/N|e|/Nσe/N|e'max|/mmPD算法8.53.24.20.25模糊迭代算法31.22.40.14

图11 未进行模糊补偿的迭代过程Fig.11 Iterative process without fuzzy compensation

图12 模糊迭代过程Fig.12 Iterative process with fuzzy compensation

图13 未进行模糊补偿的迭代过程Fig.13 Iterative process without fuzzy compensation

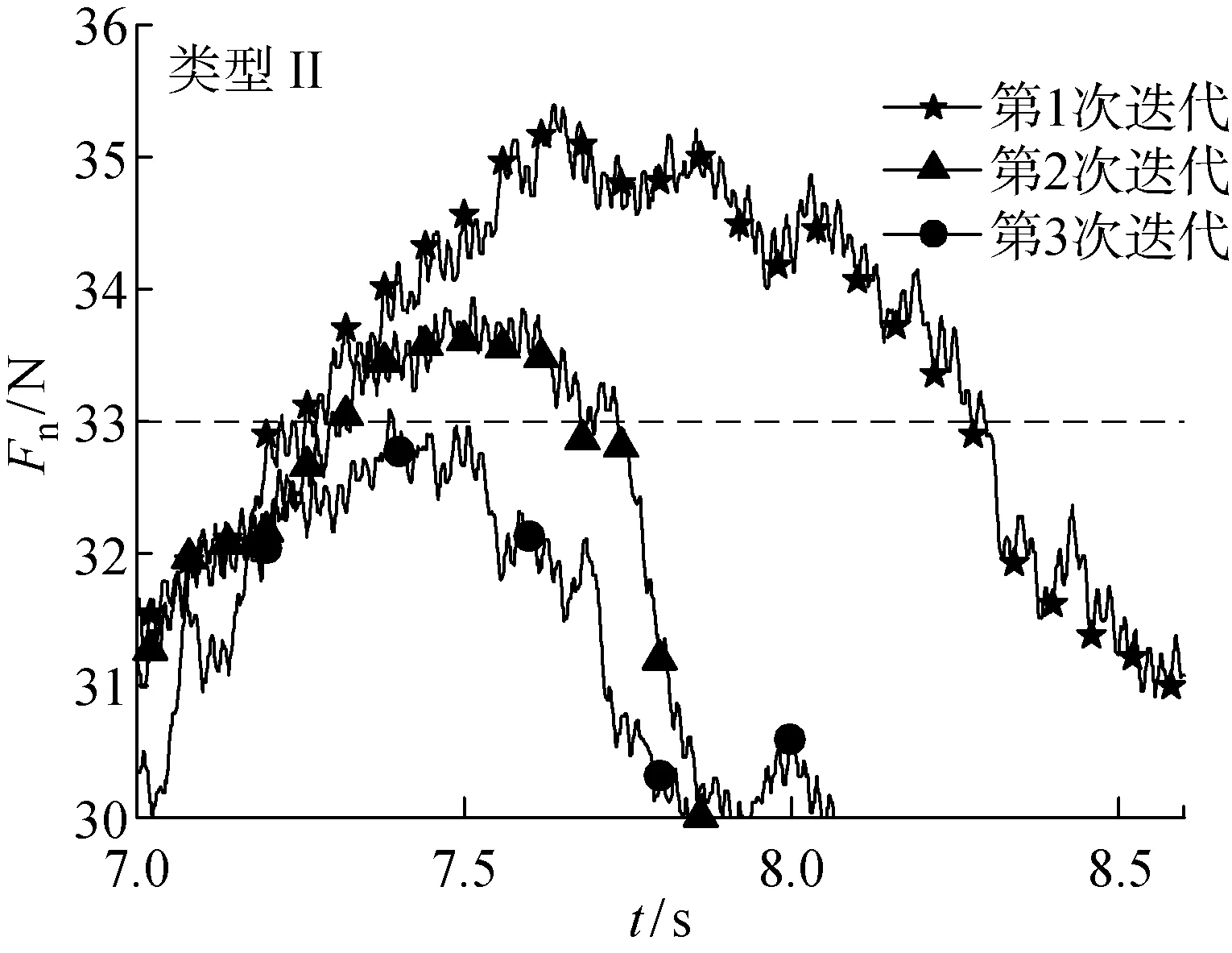
图14 模糊迭代过程Fig.14 Iterative process with fuzzy compensation

4 结论

(1) 对机器人末端执行器与曲面接触进行受力分析，得到了各个坐标系之间的映射关系，构建了法向力和传感器测量力之间的关系.

(2) 从理论上证明了提出的模糊迭代算法有界收敛，为实验提供了理论基础，实验证明了算法可行性.

(3) 模糊迭代算法表现出较好的跟踪性能，实验得到法向力在期望值±3 N内波动.相比传统的PD算法，接触力误差的均方差减少了42%，同时，曲面的跟踪精度也得到了提高.

(4) 模糊迭代算法加速了收敛过程，与未进行模糊补偿的迭代算法相比，在选择的迭代周期内，迭代次数至少减少了1次.

利用模糊迭代算法得到精确的曲面轮廓为后续机器人打磨提供了较好初始轨迹.