利用预报误差分布拟合实现卫星历史轨道机动检测的方法*
李 涛,黄 昊,陈 磊
(1. 国防科技大学 空天科学学院, 湖南 长沙 410073; 2. 军事科学院 国防科技创新研究院, 北京 100071)
在当前空间目标数量日益增长且多为非合作目标的背景下,及时发现航天器轨道机动、碰撞解体等空间事件具有重要意义。一方面,及时获知空间事件信息对及时采取合适的应对措施至关重要;另一方面,基于历史机动信息可以分析预测航天器的活动规律和机动行为,有效支撑空间态势感知。
轨道机动会引起空间目标的轨道异常,检测特定轨道参数的异常变化是从历史轨道数据中获取机动信息的有效途径。美国战略司令部发布的两行轨道要素(Two Line Elements, TLE)数据是目前为止公开发布的最完备的空间目标轨道信息编目数据。国内外学者已提出一系列从航天器历史TLE数据中检测轨道机动的方法。概括而言,这些方法分为两类。一类直接对编目轨道要素或其导出量的历史数据进行统计分析,以检出统计意义上的异常编目数据[1-4];另一类通过比较轨道要素编目值与相应预报值判断编目值是否异常[5-7],其中预报值通常通过与TLE数据配套使用的SGP4/SDP4轨道预报模型[8]得到,编目值与预报值的差,即预报误差则被作为异常值检测的指标。由于TLE本身包含误差且轨道预报模型也会引入一部分误差,因此预报误差值具有不确定性且其分布特性与预报时间有关。现有的机动检测方法并未考虑其概率分布特性,仅利用预报误差的统计均值和方差信息确定异常值检测的门限。方法中往往暗含预报误差服从高斯分布的假设,这一未经验证的预设条件可能会对预报误差异常值检测的造成干扰,进而影响机动检测的准确率。
本文提出一种基于预报误差分布拟合的机动检测方法。通过分析预报误差检测轨道参数的异常编目值,但不预设预报误差的概率分布形式,而是利用历史数据进行拟合。对目标的历史TLE数据两两预报求差获得预报误差的样本数据后,利用期望最大化(Expectation Maximization, EM)算法对样本数据拟合得到以高斯混合模型表达的预报误差的概率分布模型。随后,以此为基础设计轨道参数异常值检测方法,并利用轨道机动与轨道异常之间的对应关系实现机动检测。最后,选取典型活动卫星为测试目标进行机动检测,分析验证所提方法的可行性和机动检测性能。需要指出的是,在所设计的轨道机动检测方法中,用于分析的轨道参数的选择并不是唯一的,本文仅以卫星的轨道半长轴为例对机动检测方法进行说明,实际上也可以选择轨道倾角、偏心率、轨道能量等其他参数。
1 基于历史数据的预报误差分布拟合
1.1 样本数据的生成
预报误差样本数据的生成方法如图1所示。利用SGP4/SDP4模型,ti时刻的TLE编目轨道参数ai将被顺次外推至随后m个编目值所在的历元时刻ti+1,ti+2,…,ti+m,以得到相应的预报值ai+1,i,ai+2,i,…,ai+m,i。将这些预报值与相应的编目值相减,就得到m个预报误差数据Δai+1,i,Δai+2,i,…,Δai+m,i,以及对应的预报时间Δti+1,i=ti+1-ti,Δti+2,i=ti+2-ti,…,Δti+m,i=ti+m-ti。
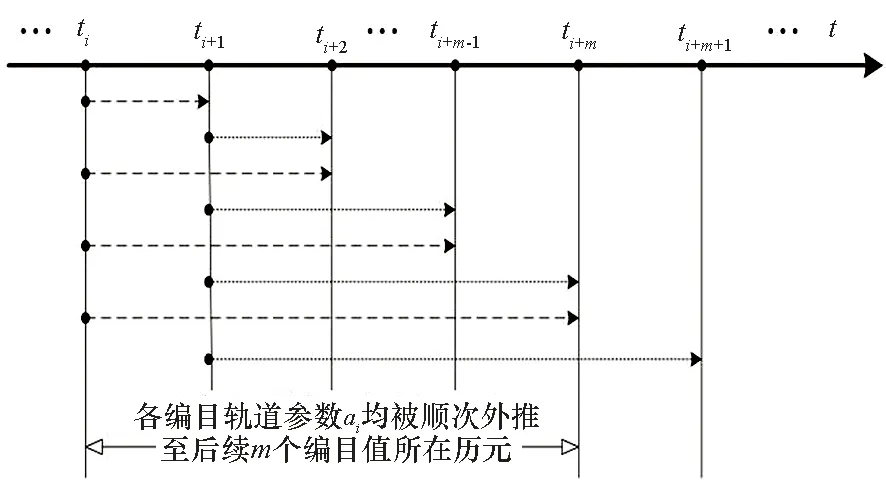
图1 生成预报误差样本数据的示意图Fig.1 Sample data generation of the prediction error
对所有容许的轨道参数编目值顺次重复上述过程,可以得到一系列与不同预报时间相对应的预报误差数据。它们构成了预报误差的样本数据,记为集合S。在生成样本数据时,可以根据实际情况确定参数m的值以获得合适的样本数据量。
由于预报误差的分布特性与预报时间密切相关,样本数据被用于分布拟合之前需要按其预报时间进行分组。考虑到同一空间目标的绝大部分TLE之间的发布时间间隔一般为轨道周期的整数倍[9],集合S中各预报误差对应的预报时间一般也近似等于轨道周期的整数倍,故各预报时间均可以与其轨道周期T的整数比值表示,再将具有相同预报时间的误差数据进行分组。假设样本数据最终被分为N个数据组,即
S={Sr1,…,Srk,…,SrN}
(1)
则Srk包含所有预报时间为rk倍轨道周期的预报误差数据。
1.2 预报误差的分布拟合
对预报误差的分布拟合包括两步:第一步是建立以高斯混合模型描述的预报误差的概率分布数学模型;第二步是利用EM算法从样本数据中学习概率分布模型的模型参数。
高斯混合模型常被用作描述随机变量概率分布的参数模型,它由有限个高斯分布的加权和构成。理论上来说,只要高斯分布的个数足够多,利用高斯混合模型可以对任意形式的概率分布进行数学描述。基于高斯混合模型,预报时间为rk倍轨道周期时,预报误差Δa的概率密度函数可表示如下
(2)
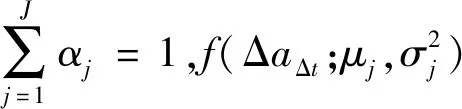
(3)
在式(2)表达的概率密度函数中,待确定的参数包括高斯分布的个数J以及各高斯分布对应的参数αj、μj和σj。文献[10]利用高斯混合模型对TLE位置预报误差的概率分布进行了拟合,结果表明高斯分布的个数取3足以得到满意的拟合效果。以此为参照,这里直接取J=3,其他参数则利用EM算法从预报误差样本数据中学习得到。
EM算法是一种迭代算法,1977年由Dempster等总结提出[12],用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。EM算法的每次迭代由两步组成:E步,求期望;M步,求极大。利用EM算法从预报误差数据组Srk中估计frk(Δa)中参数的迭代计算过程[12]如下。
输入:数据组Srk={Δa1,Δa2,…,ΔaK}及高斯混合模型frk(Δa)。
输出:高斯混合模型的描述参数αj、μj和σj。
1)取参数的初始值开始迭代。
2)E步:依据当前模型参数,计算第j个高斯成分对观测数据Δak的响应度
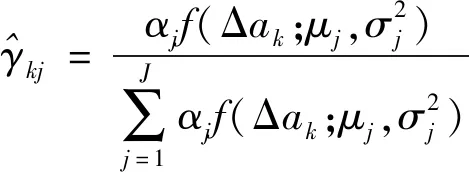
(4)
3)M步:计算新一轮迭代的模型参数
(5)
(6)
(7)
4)重复第2和第3步,直到收敛。
对数据集S中的各数据组依次重复上述拟合过程,即可得到预报时间为r1,r2,…,rN时预报误差的概率密度函数,分别记为fr1(Δa),fr2(Δa),…,frN(Δa)。考虑到样本数据过小时会影响误差分布的拟合效果,在上述拟合过程中忽略了数据量不足的数据组。
2 机动检测方法
2.1 轨道参数异常值的检测
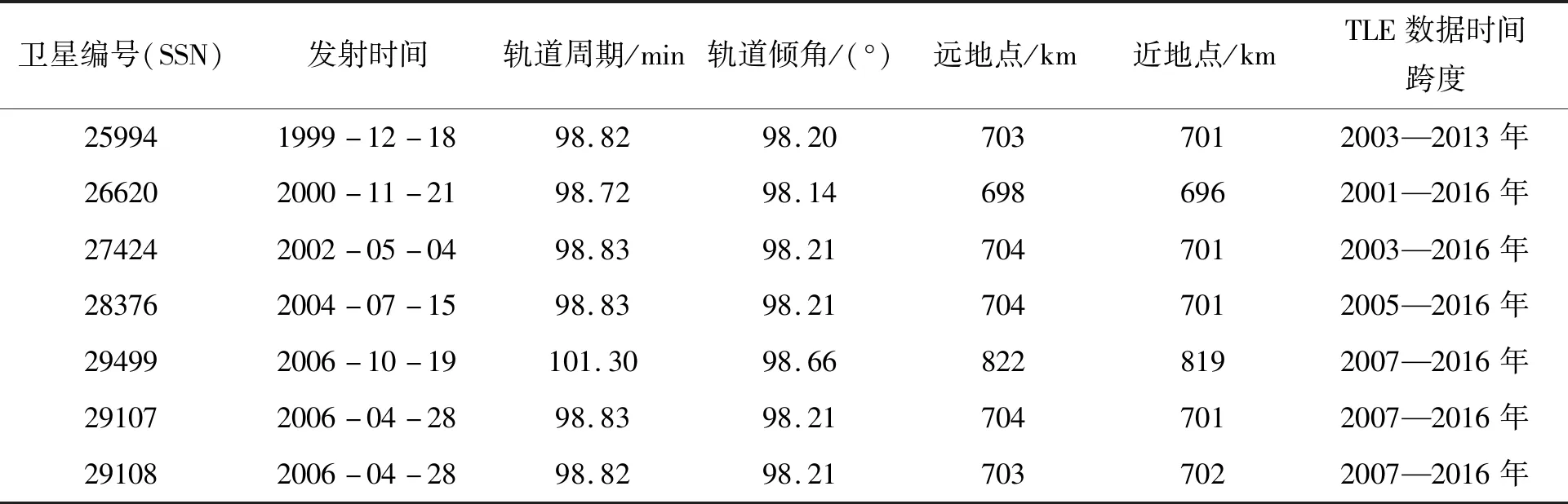
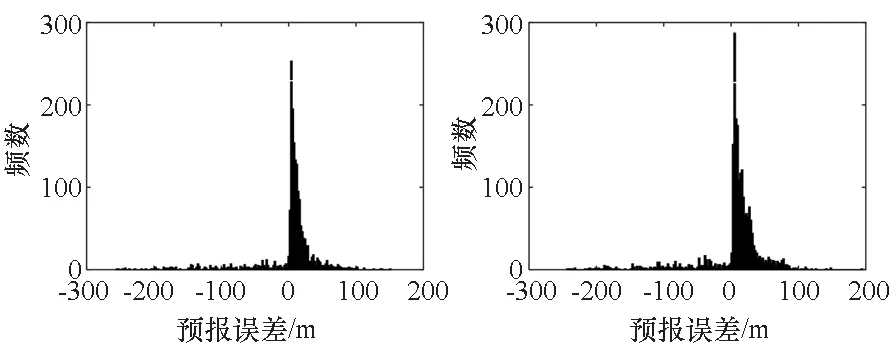
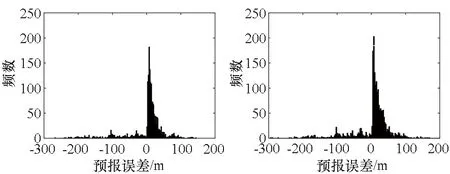
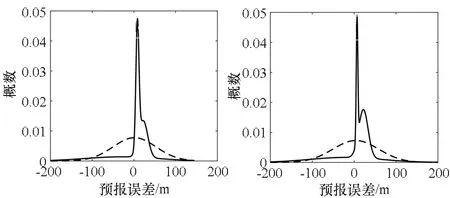
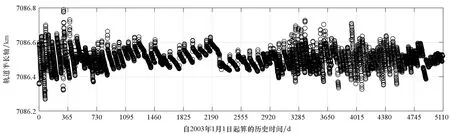
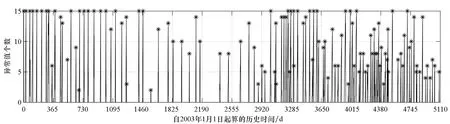
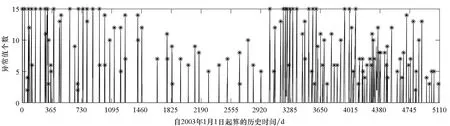
通过分析预报误差对轨道参数异常值进行检测是一种行之有效的方法,检测问题可概述为:根据将轨道参数序列的第i个编目值预报至第j个(i 根据1.1节所述样本数据的生成方法,预报误Δaj,i必定属于样本数据集S中的某数据组。假定第i个和第j个轨道参数编目值的历元时间差满足Δtj,i=rk,即等于rk倍轨道周期,则Δaj,i是数据组Srk中的元素。因此,问题变成判断Δaj,i在数据组Srk中是否属于异常值。 但是,考虑到预报误差的真实分布,即拟合得到的概率分布函数frk(Δa)并不一定满足高斯分布,因此直接应用n-σ法则进行异常值检测并不合适。这里参照n-σ法则提出一种改进的异常值检测法则,并命名为n-P法则,如图2所示。 图 2 n-P法则示意图Fig. 2 Diagram of the n-P rule n-P法则将超出区间[lbn,ubn]的数据视作异常值,类似地,n=1、2、3依次对应P1=0.682 7、P2=0.954 5、P3=0.997 3。区间[lbn,ubn]则根据概率Pn及拟合得到的概率密度函数frk(Δa)计算得到。记与frk(Δa)对应的累积概率分布函数为Frk,则lbn和ubn的计算公式如下 (8) 如果Δaj,i位于区间[lbn,ubn]之内,则认为第j个轨道参数编目值是正常的,否则它将被判定为异常值。 考虑到由任意两个满足要求(i 轨道机动会使轨道参数发生异常变化,表现为轨道参数编目值序列中的异常值。理论上来说,检出轨道参数编目值序列中的异常值,即可实现机动检测。然而,由于TLE本身包含数据噪声(这一噪声来源于轨道确定过程中用来生成TLE数据的轨道状态观测值误差以及建模过程中的不确定性),即使某个编目值被检出为异常值,并不能认定它必然是由轨道机动造成的。 在利用预报误差进行机动检测的背景下,为消除噪声干扰,一个有效的方法是将轨道参数编目值分别预报至后续多个编目值所在历元。然后根据所得的预报误差判断后续各编目值是否异常,只有随后的大部分编目值都被判定为异常时才认为这是由轨道机动造成的。 基于该思想,从卫星的轨道参数编目值序列中检测历史轨道机动的数据处理流程确定如下。 步骤1:依次选取编目值序列中的各元素为预报基准。对于每一基准数据,将其顺次外推至后续m个编目值所在历元(这里的m值与1.1节中的m值相同),根据所得的预报误差分别判断这m个编目值是否异常,并记录异常值个数。最后可以得到一个序列ID,序列ID中第i个元素记录了以轨道参数编目值序列的第i个元素为预报基准时,后续m个编目值中被检出为异常值的个数。 步骤2:对于编目值序列中与噪声对应的单个异常值,在第1步中分别以在它之前的m-1个编目值为预报基准进行异常检测时,序列ID中对应的元素值均为1。当以该异常值本身为预报基准时,序列ID中对应的元素值则为m。因此,噪声引起的单个异常值一般对应于序列ID中长度为m+1、均值约为2的非零元素数据段。为消除TLE数据噪声的干扰,从序列ID中找出由非零元素构成且元素均值不超过3的数据段,并将这些数据段中的元素值重置为0,最终得到一个新序列,记为IDm。 步骤3:IDm中的非零元素可以认为必定是由轨道机动造成的。从该序列中提取出所有由非零元素组成的数据段,每一个数据段被认为代表一个轨道机动,并且数据段中最大元素值对应的预报基准所在历元时刻被视为机动时间。 为评估所提机动检测方法的检测性能,选取7个典型的LEO轨道卫星作为测试目标,如表1所示。 表1 选定卫星概况Tab.1 Summary of selected satellites 对每一个卫星,首先将轨道参数编目值序列中所有元素分别外推至其后续15个编目值所在历元,即取m=15,以获得预报误差的样本数据。然后,利用这些样本数据拟合得到不同预报时间下预报误差的概率分布模型。然后,建立基于拟合分布模型和2-P法则建立轨道参数异常值的检测门限。最后,应用2.2节所述的检测方法对轨道参数编目值序列进行分析,检出轨道机动事件。 此外,为了验证轨道参数预报误差分布的非高斯特性,并评估该特性对机动检测性能的影响,还设计了假设预报误差服从高斯分布的对比试验。与本文所提方法相比,对比试验的唯一不同之处在于:在得到各卫星的轨道参数预报误差数据并按预报时间完成分组后,将采用高斯模型而不是高斯混合模型对预报误差的概率分布进行拟合。对比试验得到的检测结果将被用于与本文所提方法得到的检测结果之间进行对比,从而得出结论。 以27424号卫星为例对机动检测的详细过程说明如下。利用2003年1月1日至2016年12月31日的历史TLE数据,共得到128925个轨道参数预报误差数据。这些数据按照其对应的预报时间被分成196个数据组。图3给出了典型数据组的柱状图。 (a) Δti+m,i=88T (b) Δti+m,i=102T (c) Δti+m,i=116T (d) Δti+m,i=131T图3 27424号卫星典型预报误差数据组的柱状图Fig.3 Histograms of typical prediction error data groups for object 27424 随后,这些预报误差数据组被用于拟合得到分别由高斯混合模型及高斯模型表示的概率分布模型,它们构成了轨道参数异常值检测的基础。对前述数据组拟合得到的概率密度函数如图4所示。 (a) Δti+m,i=88T (b) Δti+m,i=102T (c) Δti+m,i=116T (d) Δti+m,i=131T图4 对27424号卫星典型预报误差数据组进行拟合得到的概率密度函数Fig.4 Fitted probability density functions of typical prediction error data groups for object 27424 与拟合得到的预测误差的两种概率密度函数相对应,可以得到两种轨道参数异常值的检测门限。相应地,利用2.2节所述数据处理方法对27424号卫星的轨道参数编目值序列进行处理,得到两种机动检测结果(如图5和图6所示,其中检出的轨道机动以“*”标注)。对其余6颗卫星重复上述机动检测流程,即可得到所有卫星的机动检测结果(见表2)。 由表2可知,利用人工方法检测出7个卫星共进行了520次机动。而本文所提方法成功检出了其中的478次,成功率达到了92%左右,在漏检42次机动的同时发生了7次误检。总的来说,该方法的机动检测准确率较好且能有效避免误检。 相较而言,对比试验只检测出了520次机动中的439次,成功率大致为84%,并且误检次数和漏检次数均达到本文所提方法的两倍左右。在对比试验中,实际上隐含了预报误差服从高斯分布的假设。相应地,轨道参数异常值的检测门限基于2-σ法则确定。图4及图5表明,预报误差的真实分布实际上与高斯分布相去甚远,可知假定预报误差服从高斯分布并不合适。在高斯分布假设下,尽管大部分量级较大的机动事件能被正确检出,但对于大部分小量级机动事件及部分大量级机动事件,这一假设将严重限制算法的检测性能,导致较大概率的误检和漏检。反之,基于预报误差分布拟合的机动检测方法则能取得较好的检测效果,出现误检和漏检的概率也更低。 (a) 卫星的半长轴时间-历史(a) Semi-major axis time-history (b) 检测到的异常值个数 (b) Detected number of anomaly points图5 基于本文所述机动检测方法的机动检测结果Fig.5 Maneuver detection result of our method (a) 卫星的半长轴时间-历史(a) Semi-major axis time-history (b) 检测到的异常值个数(b) Detected number of anomaly points图6 对比试验得出的机动检测结果Fig.6 Maneuver detection result of contrast test 表2所有卫星的机动检测结果 卫星编号(SSN)机动次数(人工检测)机动次数(本文方法)机动次数(对比试验)误检漏检成功误检漏检成功259946402620135126620452243611342742412301211121710528376104011930208429499362135413529107782126621464291087012681466合计5207424781581439 本文提出了一种基于预报误差分布拟合的轨道机动检测方法。该方法首先通过对卫星轨道参数编目值和预报值进行比较并分析预报误差来识别轨道参数异常值,进而得到相应的历史机动信息。在利用预报误差进行轨道参数异常值检测时,并不预设预报误差的概率分布形式,而是利用历史数据拟合得到。随后,基于拟合得到的分布模型推导得到对轨道参数异常值的检测方法。最后,根据轨道机动和轨道参数异常编目值的对应关系,提出从轨道参数编目值序列中获得历史机动的具体方法。对典型卫星的机动检测结果表明,假定轨道参数预报误差服从高斯分布并不符合实际情况,而利用高斯混合模型则可以对预报误差的概率分布进行很好的拟合。以之为基础构建的机动检测方法能够在准确检出绝大部分历史机动的同时有效避免误检事件的发生。
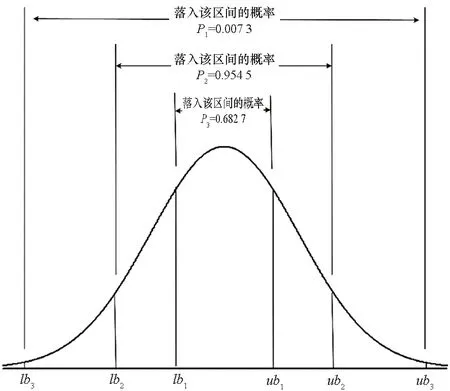
2.2 轨道机动的检测
3 算例分析
3.1 算例设计
3.2 结果分析


Tab.2 Maneuver detection results of all satellites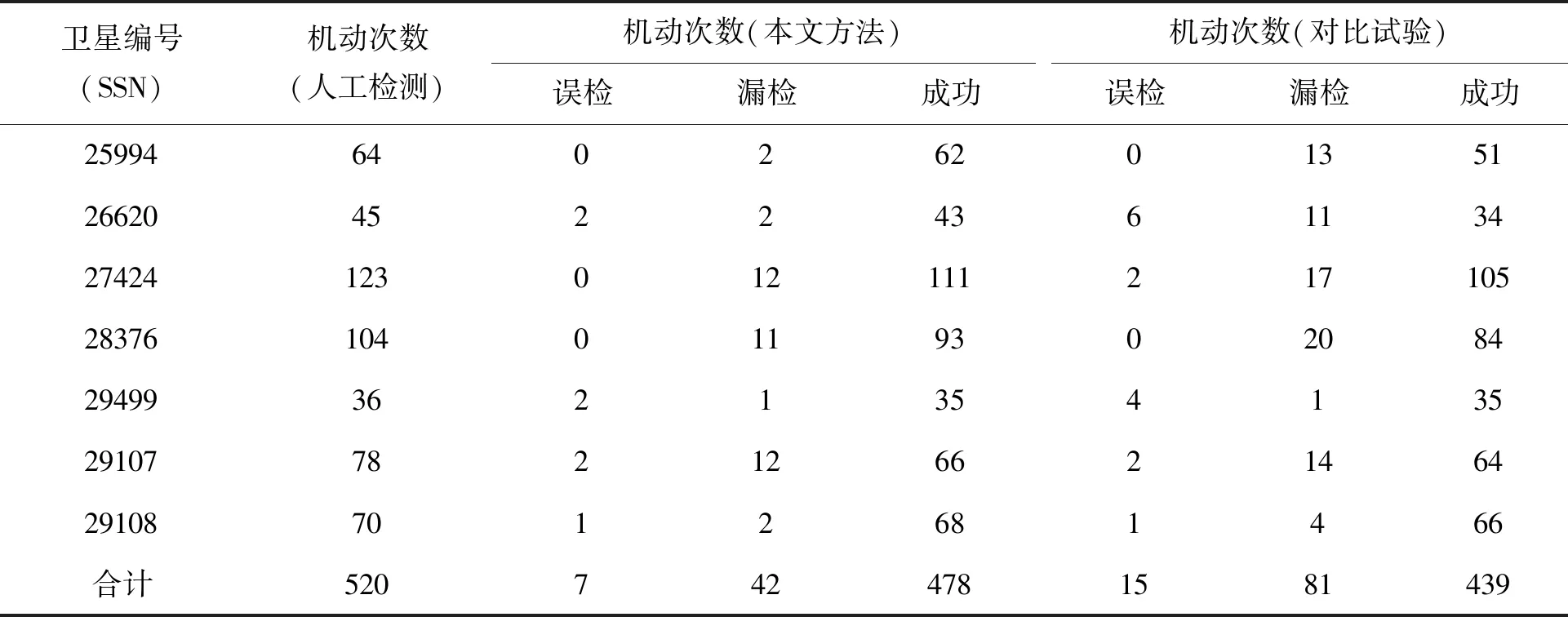
4 结论

