空间双体系绳系统展开阶段末端星姿态动力学分析*

陈书敏，王长青，扎伯罗特诺夫·尤里，李爱军

(1. 西北工业大学 自动化学院， 陕西 西安 710129； 2. 中俄国际空间系绳系统研究中心， 陕西 西安 710129；

3. 萨马拉国家研究型大学 空间与火箭技术学院， 俄罗斯 萨马拉 443082)

空间系绳系统(Space Tether System, STS)是一种可延展数十乃至上百千米的复杂动力学系统。作为一种新型航天器组合体，该系统具有广阔的应用前景。例如：利用长系绳系统可探测地球大气、重力场及磁场等[1-2]；利用系绳代替传统的刚体机械臂所构成的空间绳系机器人可执行太空垃圾捕获、拖曳离轨等太空任务[3-4]。

空间系绳系统的动力学建模是研究的重难点。建立精确的动力学模型是一个亟待解决的问题[5]。一般而言, 系绳展开是执行太空任务的第一步，也是任务成败的关键[6]。展开运动的复杂性要求对其动力学模型进行更深入细致的研究。

目前在系绳系统动力学研究领域，计入末端星姿态的系统动力学分析及控制问题研究尚不成熟。典型的系绳系统模型有连续体模型、离散模型以及刚性杆模型：连续体模型是基于偏微分方程的分布参数式模型，这类模型结果精确，但方程求解较为复杂；离散模型假设系绳由一系列离散点通过无质量弹性杆连接构成，刘壮壮等[7]建立了一种改进的离散珠式模型，具有可变自由度等特点，但是当选取的离散点足够多时，同样面临计算量过大的问题[8]；刚性杆模型可以降低模型复杂度，缩短计算时间，并能体现系绳系统的基本特性，得到了广泛应用，学者们基于刚性杆模型设计了多种系绳展开控制律[9]。总结而言，上述模型多侧重于对系统中的绳子进行建模分析，多将系绳末端连接的星体视为质点，忽略其尺寸及姿态运动。对于实际的太空任务，末端星姿态往往不可忽略。例如利用系绳系统执行近距离空间抓捕任务时，需要对系绳末端的抓捕机构及目标进行姿态分析及控制[10]。

计入末端星体姿态运动时，系绳系统的动力学与控制问题变得较为复杂。此时，系统为快-慢时变自由度动力学系统[11]。Zabolotnov[12]采用积分流形法对这类系统的快、慢变量进行了分离处理。余本嵩等[13]将释放机构视为质点，研究了系绳释放对主星姿态的影响。Pang等[14]指出在一定的参数条件下，系统中的主星姿态将产生混沌运动。朱仁璋等[15]研究了状态保持阶段的子星振荡与姿态运动。Liu等[16]针对短系绳建立了考虑子星姿态的动力学模型，并利用推力对子星姿态进行稳定控制。Gou等[17]针对展开过程子星姿态不稳定问题，采用分数阶控制设计了姿态稳定控制器。上述研究对系绳一端星体(母星或子星)的姿态进行了分析，但未将母星及子星的姿态进行综合考虑，且忽略了系绳展开与末端星姿态之间的耦合作用，而这种耦合作用可能导致系绳展开时缠绕卫星，因此有必要对此加以研究。

研究末端星的姿态运动时，需要考虑星体动/静不对称性所造成的影响。静不对称性是指系绳连接点与星体惯性轴之间的偏差，动不对称性则是衡量刚体质量惯性特性不均匀性的指标。王长青等[18]采用欧拉-牛顿方法建立了考虑子星姿态的系绳系统数学模型，并基于该模型研究了子星静不对称的影响，但采用欧拉方程建立的姿态模型存在章动角奇异的情况。在卫星制造过程中，通常存在动/静不对称性；且在系绳系统运行过程中，若产生质量损耗或突变(如捕获)，星体不对称性将发生变化，因此需要研究星体不对称性对系绳系统运动的影响。

本文研究空间双体系绳系统展开过程中末端星体姿态的动力学问题，贡献在于：①将系统中母星及子星视为尺寸不可忽略的刚体，推导出计入末端星姿态的系统展开数学模型，并考虑了系绳展开与末端星姿态运动之间的耦合作用; ②利用所得模型研究了系绳系统展开过程中末端星的角运动，以及存在初始扰动及动/静不对称性时的动力学特性。

1 动力学建模

本文研究的空间系绳系统由系绳连接母星和子星构成，如图1所示。为描述系统的展开运动，需要用到下列坐标系：①OXYZ，地心赤道坐标系；②OX0Y0Z0，地心轨道坐标系；③cx0y0z0，轨道运动坐标系，原点位于系统质心，初始时刻各轴与OX0Y0Z0平行；④cxtytzt，系绳坐标系，cxt轴沿系绳方向，指向母星，cxtyt平面与母星及子星矢径Ra和Rb所张成的平面共面；⑤cixiyizi(i=1,2)，末端星本体坐标系，原点固连于末端星质心处，各坐标轴沿星体惯性主轴方向。由系绳坐标系通过“x-z-x”顺序旋转可得到本体坐标系，相应的旋转角分别为末端星姿态角：进动角ψi、章动角αi以及自旋角φi。

图1 空间双体系绳系统示意图Fig.1 Diagram of STS

为简化模型推导过程，假设：

1)系统运行轨道为圆轨道，且运行轨道升交点赤经Ω及轨道倾角i不变。

2)仅考虑万有引力力矩与系绳张力力矩作用，忽略重力梯度及外部干扰作用影响。

3)系绳视为轴向不可承受压力的刚性杆。

由于系绳展开多在一个或几个轨道周期内完成，时间相对较短，因此质心轨道参数的变化幅度及外部干扰力矩的影响很小，可忽略不计。此外，展开过程中系绳保持张紧，张力始终为正值，不会出现系绳压缩的情况，故可将系绳视为刚性杆。

根据第二类拉格朗日方程，有：

(1)

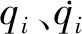
系统动能为：

T=T1+T2

(2)

其中，T1表示母星动能，T2表示子星动能。

建模时，假设系绳展开速度与展开方向平行，即VL1与L1共线，则母星动能T1为：

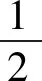
Vc·(ω1×Rc1)m1+VL1·(ω1×Rc1)m1+

Vc·VL1m1+(ωt×L1)·(ω1×Rc1)m1+

Vc·(ωt×L1)m1

(3)

子星动能表达式与母星形式一致，因此将下角标1均用2替换，可得出子星的动能为：

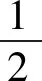
Vc·(ω2×Rc2)m2+VL2(ω2×Rc2)m2+

Vc·VL2m2+(ωt×L2)·(ω2×Rc2)m2+

Vc·(ωt×L2)m2

(4)

其中：L1表示从系统质心c指向母星连接点a的矢量，L2表示从c点指向子星连接点b的矢量，且假设L1与L2共线；Vc表示系统质心速度，VL=VL1=-VL2表示系绳展开速度；ωt为系绳坐标系的旋转角速度，ωi(i=1,2)表示星体本体坐标系的旋转角速度；Rci(i=1,2)分别表示从母星及子星连接点指向相应星体坐标系原点的矢量；Ji(i=1,2)为星体的惯性张量矩阵。

于是有：

(ωt×L1)2m1+(ωt×L2)2m2+

(ω1×Rc1)2m1+(ω1×Rc2)2m2+

Rc1)m1+2VL2(ω2×Rc2)m2+2(ωt×L1)·(ω1×Rc1)m1+2(ωt×L2)·

(ω2×Rc2)m2

(5)

其中，

(6)

这里，Jt为系绳系统的惯性张量矩阵，形式为：Jt=diag(0,Jty,Jtz)。

计入系绳质量：mt=ρL，其中，ρ表示系绳线密度，L为系绳展开长度，L=L1+L2。则系绳系统的主惯性矩为：

(7)

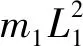
(8)

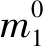
(9)

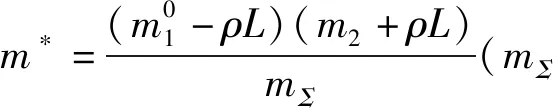
相对于系绳长度而言，Rci(i=1,2)均为小量，因此可忽略Rci(i=1,2)及其比例项，以简化系统动能表达式。最终可得系统动能为：

(10)

这里，Vc=RcΩ(Rc表示系统质心距地心的距离)。

系统势能表达式为：

Π=Π1+Π2+Πt

(11)

其中，Πt表示将末端星体视为质点时的系统势能(即末端星质心的位置势能)，Π1、Π2分别表示将母星、子星视为有限尺寸刚体时的空间姿态势能。

作用在系绳系统上的万有引力为：

(12)

其中，ma=m1+mL1为母星与系绳段L1的总质量，mb=m2+mL2为子星与系绳段L2的总质量，Kg为地球的万有引力常数，ri(i=1,2)表示地心到末端星质心的距离，可由几何关系求出：

(13)

式中，θ、β分别表示系绳的面内角与面外角，γi为矢量Rc与Rci的夹角，δi为Li与Rci的夹角。

(14)

积分后可得母星及子星质心的位置势能为：

(15)

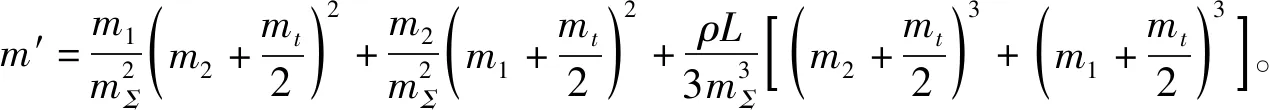
(16)

其中，ξ1i、ξ2i、ξ3i表示星体坐标系各轴偏离地垂线的角度，ξ1i=arccos(DΣi1,1),ξ2i=arccos(DΣi1,2),ξ3i=arccos(DΣi1,3)。这里，矩阵DΣi为坐标系cixiyizi与惯性系之间的转换矩阵。

将上述各分项代入方程式(1)中，可得：

(17)

式中：i=1,2，…，8；q=(α1,2,ψ1,2,φ1,2,θ,β)。

同理，还可得出系绳展开时绳长L满足：

(18)

其中，Fc表示系绳张力。

根据各坐标系间转换关系，还可得末端星及系绳的角速度满足下列运动学方程：

(19)

(20)

综上，联立式(17)～(20)，即得计入末端星姿态的空间双体系绳系统展开阶段数学模型。

2 系绳系统展开控制律

本文在忽略展开控制机构工作误差的情况下，通过参数优化得出标称展开控制力[19]：

利用粒子群优化算法得出各参数取值为：a=4.6,b=3.5,c=1.6,Tmin=0.02 N,Tmax=2.1 N,T1=0.243 N,δ1=6000 s,k=0.002。

3 数值仿真分析

3.1 仿真条件

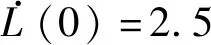
考虑到母星及子星的质量与尺寸，设母星和子星与系绳连接点位置分别为Δ1=(2 m,0 m,0 m) ，Δ2=(0.2 m,0 m,0 m)；惯性张量矩阵(单位为kg·m2)分别为J1=diag(15 000,35 000,35 000)，J2=diag(0.256,0.32,0.32)。

3.2 仿真结果及分析

3.2.1 模型校验

为验证所得数学模型的正确性，与文献[17]中所采用的简化模型进行对比。在相同控制律作用下，得到系绳展开结果如图2、图3所示。

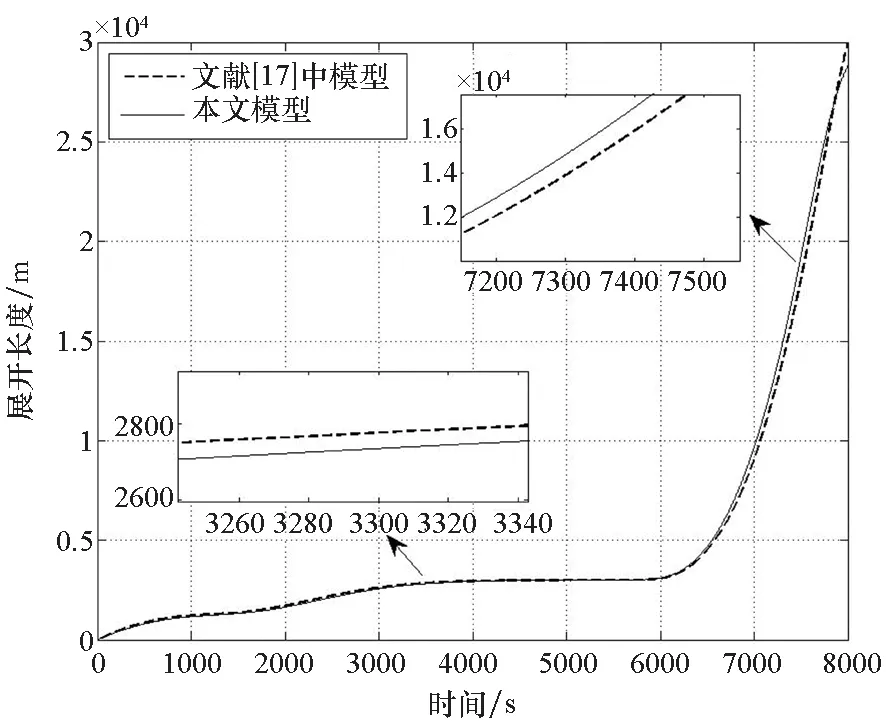
图2 展开绳长对比曲线Fig.2 Comparison curves of deployed lengths

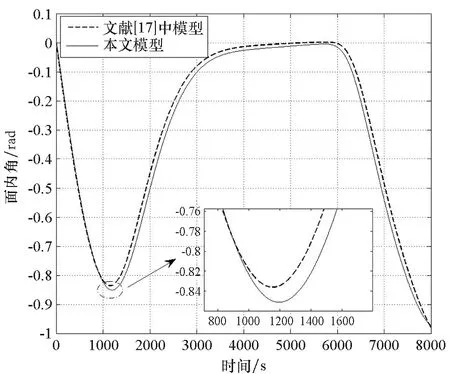
图3 展开时面内角对比曲线Fig.3 Comparison curves of in-plane angles in deployment

由图2～3可知，根据参考模型及本文模型所得到的展开过程绳长及面内角变化曲线均基本吻合。相较于文献[17]中的模型，利用本文模型计算的绳长偏差约为0.05 km，面内角偏差约0.01 rad，存在小量偏差的原因在于本文模型计入了星体姿态，这会对展开过程造成影响。据此可证明本文所建立的数学模型的有效性。

3.2.2 初始姿态角扰动的影响

下面利用所建立的模型研究展开过程中末端星的姿态运动。根据姿态角的定义，在系绳系统的展开过程中，章动角的大小能作为衡量系绳是否缠绕星体的重要依据，因此下面将重点研究章动角的运动特性。首先研究初始扰动近似为0的情形。图4为初始章动角α0=0.000 1 rad时子星章动角的变化曲线，由图可知，这种情况下，展开过程中子星章动角始终近似为0。

图4 子星章动角变化曲线Fig.4 Curve of nutation angle of sub-satellite

接下来研究初始姿态角扰动增加的影响。图5所示为α0=0.1 rad时子星章动角及其相轨迹曲线。由图5可知，子星章动角在系绳快速展开阶段达到最大值0.129 rad。与图4对比可知，随着初始扰动的增加，展开过程中章动角及其峰值随之增加。由图5可知，此时章动角相轨迹近似呈稳定的极限环，子星姿态未失稳。总结而言，当初始姿态角为小扰动时，子星相对系绳的摆动呈现小振幅高频性质，子星姿态保持稳定。这是由于子星的质量惯性特性较小，因此影响其姿态运动的主要力矩为系绳张力力矩。如图6所示，章动角的变化与系绳张力变化具有同步性，子星姿态有沿系绳张紧方向稳定的趋势。

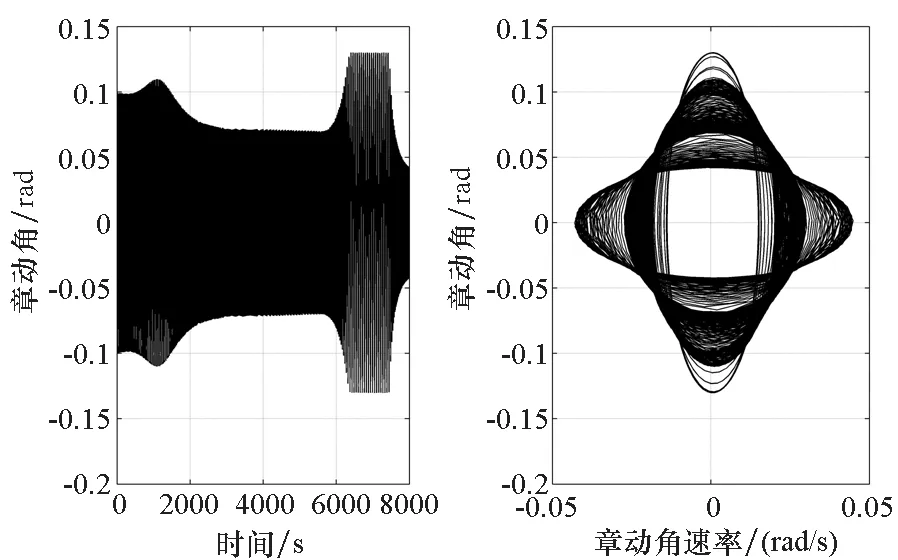
图5 子星章动角曲线及其相位图Fig.5 Curve of nutation angle and phase diagram of sub-satellite

图6 系绳张力及张力力矩变化曲线Fig.6 Curves of tether tension and tension torque

然而，继续增加初始扰动将破坏这种稳定性。图7所示为α0=0.8 rad时的章动角曲线。此时，展开过程中的章动角变化剧烈，最大值为1.38 rad，接近所允许的章动角临界值(π/2 rad)。考虑到子星为有尺寸的刚体，这会使得系绳与子星表面接触并发生缠绕，导致展开失败。

图7 子星章动角变化曲线Fig.7 Curve of nutation angle of sub-satellite

3.2.3 动/静不对称性影响研究

上述结果是基于子星为动力学对称体，且与系绳连接点位于本体坐标系c2x2轴上的假设得到的。然而，实际的航天器并不是理想的对称旋转体，与系绳的连接点位置也存在偏差。

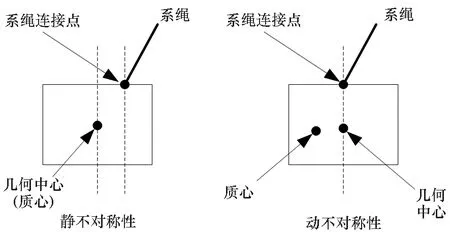
图8 末端星体静/动不对称性示意图Fig.8 Static/dynamic asymmetry of end-bodies

首先研究静不对称性的影响。设初始章动角为0，取六组数据表征静不对称性大小，静态误差Δ分别为0.001 m、0.005 m、0.01 m、0.05 m、0.08 m、0.1 m,其余初始条件不变，对比分析子星章动角变化曲线，如图9所示(图中静不对称性从左至右、从上至下依次增大)。

(a) Δ=0.001 m (b) Δ=0.005 m (c) Δ=0.01 m

(d) Δ=0.05 m (e) Δ=0.08 m (f) Δ=0.1 m图9 子星章动角对比图Fig.9 Comparison of the nutation angles of the sub-satellite

仿真发现，当存在上述静态误差时，系统均能顺利展开，且系绳展开特性变化不大，绳长及面内角的变化参见图2～3。末端星章动角幅值随静不对称性增加变化明显，呈增加趋势，如图9所示。表1给出了上述六组仿真条件分别对应的章动角及张力力矩最大值。对于给定的初始条件，当Δ=0.09 m时，最大章动角即已达90°。此外，张力力矩沿cz轴的分量也随之增加。

表1 章动角及张力力矩最大值Tab.1 The maximum of nutation angle and tension torque

(a) 子星姿态(a) Attitude of sub-satellite

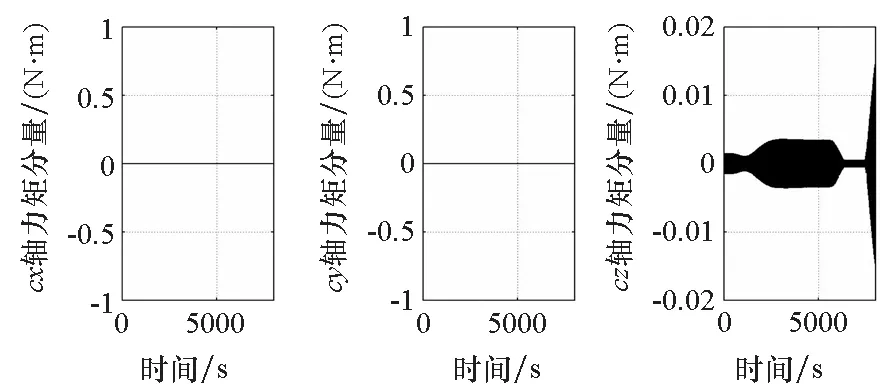
(b) 张力力矩(b) Tension torque图10 惯性积为0时子星姿态和张力力矩Fig.10 Attitude of sub-satellite and tension torque when its inertia product is 0

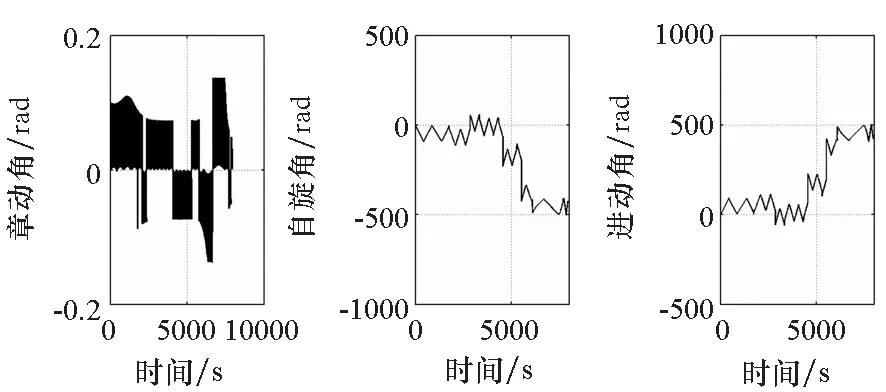
(a) 子星姿态(a) Attitude of sub-satellite

(b) 张力力矩(b) Tension torque图11 惯性积为0.001 kg·m2时的子星姿态和张力力矩Fig. 11 The attitude of sub-satellite and tension torque when its inertia product is 0.001 kg·m2

(a) 子星姿态(a) Attitude of sub-satellite

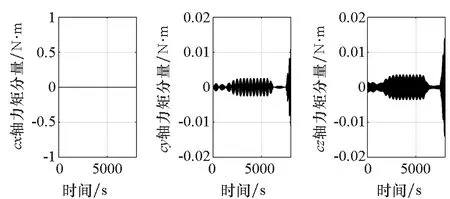
(b) 张力力矩(b) Tension torque图12 惯性积为0.01 kg·m2时的子星姿态和张力力矩Fig.12 Attitude of sub-satellite and tension torque when its inertia product is 0.01 kg·m2

接着增加动不对称性，设ΔJ=0.05，Jxy=Jyz=Jxz=0.05，子星初始章动角α0=0.1 rad，子星章动角变化如图13所示。由图可知，当子星不是对称旋转体，具有动不对称性时，姿态运动较为复杂，章动角除了高频振荡外，还出现类似标准摆运动的低频振荡，即章动角振荡振幅呈周期性变化，且随着不对称性增加，展开过程中章动角幅值可超过90°，导致系绳缠绕末端星。

图13 子星章动角变化曲线Fig.13 Curve of nutation angle of sub-satellite

需要指出的是，上述仿真中子星的不对称性对母星姿态影响不大。与子星相比，母星姿态角变化缓慢但幅值较大。这是由于母星质量惯性远大于子星，子星的不对称性所产生的力矩不足以对母星运动特性产生实质性影响。随着母星惯性特性减小，系绳张力力矩对母星角运动的影响作用将会增加。图14为母星章动角变化曲线对比图，其中图14(a)所对应的母星惯性是图14(b)的10倍。对比表明，随着惯性减小，母星最终将同子星一样沿系绳方向稳定，并做小振幅高频振荡。这表明，当末端星质量相近时(如系绳连接纳卫星所构成的系统)，在合适的张力控制律作用下，系统中所有末端星角运动均有沿系绳方向稳定的趋势。

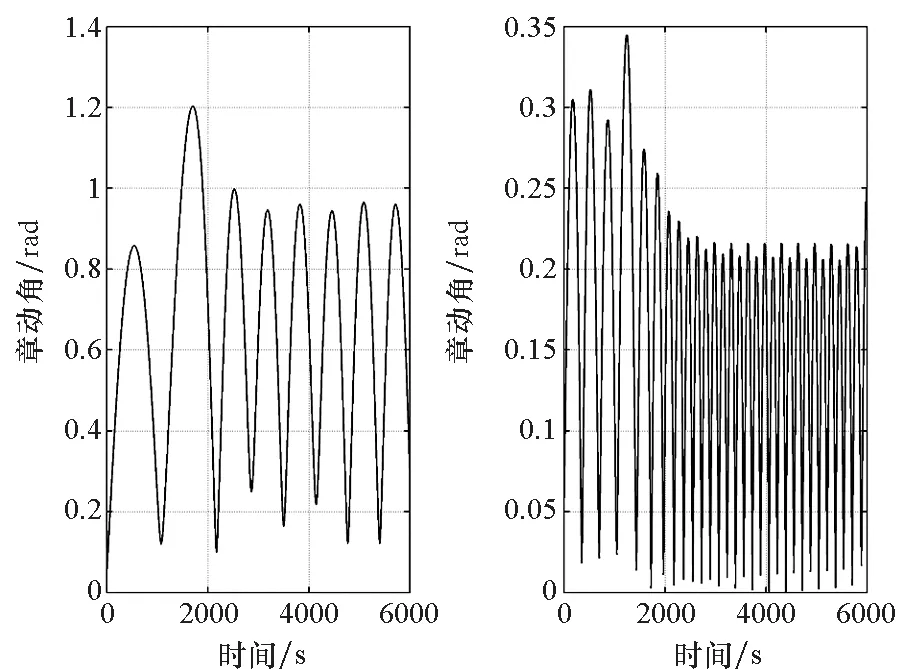
(a) J1=diag(0.256,0.32,0.32)kg·m2 (b) J′1=0.1J1 图14 母星章动角变化曲线对比图Fig.14 Comparison of nutation angle of mother-satellite

4 结论

本文研究结果表明，对于大质量比空间系绳系统，当子星对称时，其姿态角变化趋势与系绳张力同步，且子星最终沿系绳方向稳定。当子星存在静不对称性时，姿态角幅值增加，且随着静不对称性增加而增加，张力力矩增大，章动角曲线剧烈振荡，在受到扰动时，章动角可能超过90°，引起子星与系绳缠绕。当子星具有动不对称性时，会引起类似标准摆形式的低频振荡。由于在实际的空间系绳系统中，燃料消耗等因素会使得卫星质心及转动惯量等发生变化，因此开展空间试验时需要考虑动/静不对称性对子星姿态的影响，并对其姿态运动进行振荡抑制。此外，随着母星质量惯性减小，母星的姿态运动趋势与子星趋同，章动角变化曲线的幅值减小，振动频率增加，并有沿系绳方向稳定的趋势。