流水的浮点倒数近似值运算部件的设计与实现*
何 军,王 丽
(上海高性能集成电路设计中心, 上海 201204)
浮点运算部件是微处理器的重要运算部件,与处理器的性能直接相关。常见的浮点运算包括浮点加、减、乘、乘加等。这些浮点运算在传统的科学计算和工程计算应用领域中应用十分广泛。相对于这些常见的浮点运算,浮点倒数运算并不很常用,但是在数字信号处理、多媒体、计算机图形计算等应用领域,以及部分科学计算应用领域,却比较常用,也是一种重要的运算[1]。此外,利用浮点倒数运算,还可以实现浮点除法运算。
常用的实现浮点倒数运算的算法与浮点除法类似,有基于减法运算的数字迭代算法[2]、SRT算法[3-4],也有基于乘法运算的Newton-Raphson算法和Goldschmidt算法[5-6]。基于这些算法,如果要实现浮点单精度或双精度浮点倒数运算,为了减少硬件开销,一般都是采用非流水的硬件迭代方法实现。其中基于减法的迭代算法是线性收敛的,每次可以迭代出1(基数为2)、2(基数为4)、3(基数为8)位结果,硬件开销小。基于乘法的迭代算法是二次收敛的,每次迭代后结果的精度翻倍,硬件开销大。
但在有的应用中,其实并不需要非流水的全精度的浮点倒数运算,而是能流水的部分精度(比如6~10位有效尾数)的浮点倒数近似值运算。再利用流水的快速浮点乘法运算,软件实现Newton-Raphson算法和Goldschmidt算法,就可以更高效地流水地实现任意精度的浮点除法运算等其他运算。这种方法尤其适用于低精度浮点运算应用。以单精度浮点(24位尾数,含隐含位)除法运算为例,目前硬件非流水实现,需要17拍。假设利用流水的浮点倒数近似值运算,得到8位精度尾数需要6拍,再加上一次乘法运算(6拍流水执行),如果低精度应用只需要8位精度即可,则一次除法只需要12拍,且可流水执行。假设有n次这样的除法运算,使用非流水硬件实现,需要17n拍,利用流水的浮点倒数近似值运算加乘法运算实现,只需要12+n-1拍。当n越大时,流水硬件实现延迟更短。
因此,综合考虑运算延迟和硬件开销,采用基数为4的SRT算法[7-9](简称“SRT-4算法”)设计并实现了一种浮点倒数近似值运算部件(简称“FREC部件”),6级流水线结构,运算结果精度至少为8位有效尾数。为了硬件支持浮点非规格化浮点数[10-11],经过进一步改进,增加源操作数预规格化和结果后规格化功能,可以实现对浮点非规格化浮点数的硬件处理,有利于进一步提高浮点倒数近似值运算的性能[12]。
1 设计与实现
1.1 SRT-4算法
基本的SRT算法迭代过程采用数学公式描述如下(其中,X为被除数,D为除数,R为算法的基数):
RP0=X
Pi+1=RPi-qi+1D
(1)
这里Pi是第i次迭代后的部分余数,在每次迭代中,商值qi+1由商值选择函数δ决定:qi+1=δ(RPi,D),经k次迭代后最后的商Q和余数Pr(Pk为k次迭代后的部分余数)分别为:
(2)
具体实现时,SRT算法步骤如下:
1)将部分余数的初始值设为被除数X,在第i步,通过将除数D与当前部分余数比较,选择下一位商数qi+1(由商值选择函数δ决定);
2)按照递推式(1)计算出下一个部分余数Pi+1;
3)按照前两步,经k次迭代后,将所得的商数加权求和就得到最终的商Q,见式(2)。
一般基数R=2n,每次迭代可以得到的n位数商数。需要迭代的次数k与需要得到的结果精度有关。当R=4时,每次迭代可以得到2位商数;对于单精度浮点数,k=12,对于双精度浮点数,k=27。
商值选择函数δ是SRT算法的关键部分,一般采用查询表的方式实现,即根据部分余数和除数的高若干位查表得到商。对于SRT-4算法,商数集合为{-2,-1,0,+1,+2},可以采用表1所示的查询表[13],利用部分余数的高7位和除数的高4位(由于规格化的除数整数部分默认为1,因此这里的高4位实际是尾数的高4位)查表,即可得到商数。

表1 SRT-4商值查询表[13]Tab.1 The SRT-4 quotient look-up table[13]
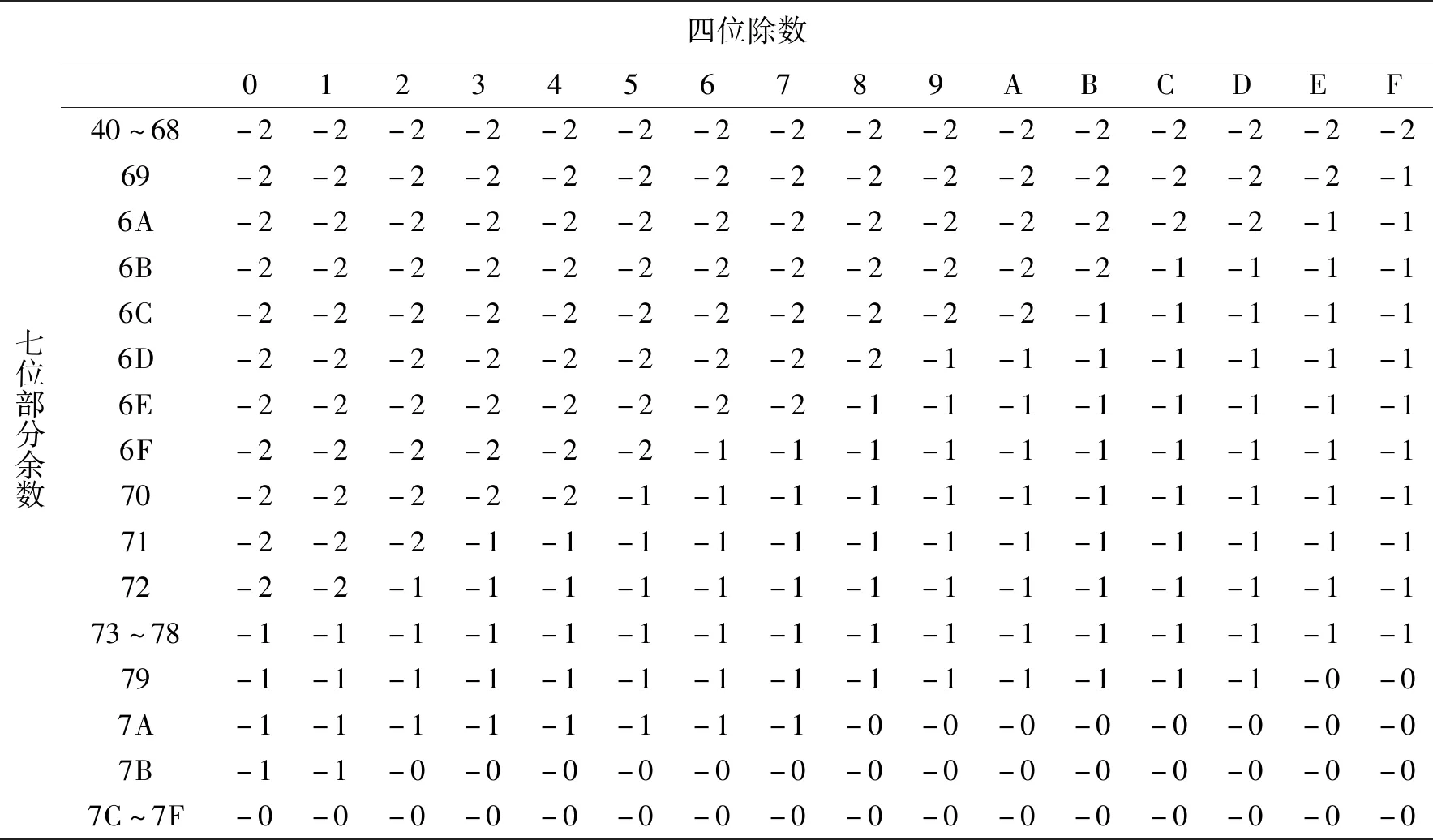
表1(续)
为了减少延迟,部分余数一般采用保留进位(carry save)的冗余形式保存在两个寄存器Carry和Sum中,避免迭代过程中的进位加法运算。所以在查表前,需要一个普通的7位进位传递加法器(Carry Propagate Adder, CPA),得到实际的部分余数,然后再查表,得到商数,如图1所示。

图1 SRT-4商值选择函数的实现Fig.1 Implement of SRT-4 quotient selection function
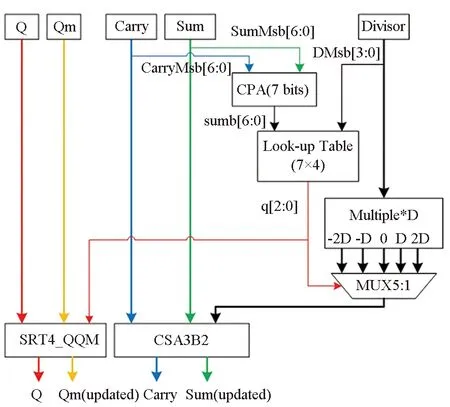
图2 SRT-4算法迭代部分原理图Fig.2 Schematic diagram of iterative part of SRT-4 algorithm
对于一次SRT-4迭代来说,其实现原理如图2所示。查表得到的商数q采用3位编码表示。根据商数q,选择得到多倍除数,并利用进位保留加法器(CSA3B2)得到更新后的部分余数Carry和Sum;同时并行得到最新的商。这里商也采用了冗余形式保存在两个寄存器Q和Qm中,两者始终相差1,即Qm=Q-1。利用飞速转换(on-the-fly)技术[14],每得到商数q,就对当前的寄存器Q和Qm值进行更新,得到新的商。其转换表参见表 2,由SRT4_QQM模块实现。

表2 SRT-4飞速转换Tab.2 The SRT-4 on-the-fly conversion
注:1)对于浮点倒数近似值运算,只需要保留10位商即可。
2){Q[7∶0],2′b00}是按位拼接运算,2′b00表示2位二进制数,下同。
1.2 FREC部件结构
FREC部件采用了SRT-4算法,为了得到至少8位有效尾数精度,考虑到首次商的最高位可能为0,因此需要经过5次迭代,得到10位有效尾数。FREC部件结构如图3所示。采用全流水实现,执行延迟为6拍,前5拍(ST0~ST4)分别进行5次SRT-4迭代(流水进行),最后一拍(ST5)进行结果输出处理。与其他浮点运算一样,实际包括两条数据通路,分别进行输入异常数据和正常数据的处理,最后两条通路数据二选一输出(输入异常优先)。其中F_REC_EXCEP模块进行输入异常数据处理,主要进行无效操作(INV)、除数为零(DBZ)、非规格化浮点数(DNO)三种输入异常检测和处理。F_REC_EXP模块主要进行阶码计算,并检测是否发生上、下溢出异常。
第一次迭代时,商值寄存器Q、Qm初始化为0,部分余数寄存器Carry初始化为0,部分余数寄存器Sum初始化为浮点数1.0(即0×3ff0_0000_0000_0000)规格化的尾数Sum_norm,除数寄存器Divisor初始化为规格化的除数尾数Divisor_norm,这里:
1)Sum_norm={3′b000,1′b1,52′b0,1′b0},即浮点数1.0的尾数;
2)Divisor_norm={2′b00,1′b1,Divisor[51:0],2′b00}。
结果输出处理主要完成如下功能:
1)利用普通加法器计算出实际的余数,根据余数判断是否发生非精确结果异常,并根据余数的符号决定是否需要恢复余数(再加上除数即可),并选择Q、Qm之一为最终的商。
2)根据商的最高位是否为0,决定是否需要将商进行再规格化(左移1位),同时将结果的阶码减1,得到正常数据通路的结果。
3)再跟输入异常处理通路的结果二选一输出(输入异常结果优先),作为最终的结果。
由于是求浮点倒数的近似值,为了简化硬件设计,仅支持向零舍入(即截断舍入)模式。
1.3 硬件支持非规格化浮点数的改进
根据IEEE-754标准[15],规格化浮点数X=(s,e,f)形式化表示如下:
X=(-1)s×2e-bias×(1.f)
这里,0 图3 FREC部件结构Fig.3 Implementation of FREC unit 非规格化浮点数X=(s,e,f)形式化表示如下: X=(-1)s×21-bias×(0.f) 这里,e=0,f≠0。两者可统一表示为: X=(-1)s×2e+~x0-bias×(x0+0.f) 这里x0为尾数部分隐含整数位,对于规格化浮点数,其取值为1;对于非规格化浮点数,其取值为0。~x0表示x0取反。 一般浮点硬件仅支持规格化浮点数的运算,如果需要支持对非规格化浮点数的运算,需要进行特殊处理[10-11]: 1)对输入的非规格化浮点数要进行预规格化(pre-normalization)处理,检测尾数头1的位置,然后将尾数左移,直到最高位为1,同时减少阶码; 2)当运算结果为非规格化浮点数时,需要进行后规格化(post-normalization)处理,常规的浮点运算需要对结果的尾数进行规格化左移,直到最高位是1为止。但是,如果发现此时的阶码出现了下溢(即小于最小阶码emin)还需要再右移尾数,并增加阶码,直到阶码等于emin。 1.3.1 源操作数预规格化 对非规格化浮点数的尾数(包括隐含的整数部分)进行头零检测(Leading Zero Detection,LZD),假定头零个数为m(规格化数m=0,非规格化数m>0),将尾数左移m位,保证尾数最高位为1。非规格化浮点操作数阶码为0,而实际的阶码是1,调整后的阶码为(1-m)。对于规格化浮点数,不需要进行预规格化,直接进行运算即可(参见图 4)。 图4 源操作数预规格化Fig.4 Source operand pre-normalization 1.3.2 结果后规格化 经过预规格化,非规格化浮点数的运算结果的尾数与规格化浮点数一样,头0的个数最多为1,只需要规格化左移1位,同时将结果的阶码减1,即可得到最终的尾数fr和阶码er。这里er可能小于等于emin,即结果发生了下溢,可能是非规格化浮点数。 为了得到非规格化浮点数结果,需要对结果进行后规格化,即将结果的尾数右移,同时增加结果的阶码,直到阶码等于emin。不妨设假定n=emin-er(er≤emin),p为浮点尾数有效位宽(对于单精度浮点数p=23,对于双精度浮点数p=52,对于这里倒数近似值运算来说,实际p=9),反规格化右移位数y与结果尾数的精度p有关: 1)若n<(p+1),则y=n(当n为0时无须右移); 2)若n≥(p+1),则y=p+1(此时如果再继续右移,实际上结果的尾数已经为0,不必再右移了)。 当右移位数超出精度p+1,导致移位后有效尾数为0,此时阶码也应为0,即最终结果为0。当结果为非规格化浮点数时,也属于发生下溢,会报告下溢异常。结果后规格化功能的实现参见图5。 图5 结果后规格化Fig.5 Result post-normalization 为了硬件支持非规格化浮点数处理,在FREC部件正常运算通路开始之前对源操作数进行预规格化(需要增加1拍),在结果输出处理模块之前,增加结果后规格化(也需要增加1拍),最终FREC部件新增2级流水线,执行延迟变为8拍。 此外,对输入异常数据处理模块F_REC_EXCEP也进行了适当修改,不再把非规格化浮点数直接当同符号的0进行处理。 浮点倒数近似值运算的正确性验证,是以已经验证正确的浮点除法为参考模型,将被除数固定为浮点数1.0,除数与倒数运算的源操作数相同,然后截取除法结果的高8位有效尾数进行验证。源操作数采用浮点典型特殊值和随机值相结合的方法,进行大量模拟验证。此外,针对算法实现撰写了功能点,功能覆盖率可达到100%。还进行了代码覆盖率分析,也可达到接近100%(部分底层公共子模块存在覆盖不到的情况,也进行了确认)。结果表明,浮点倒数近似值运算部件的功能是正确的,结果的精度也符合预期。 利用Synopsys的Design Compiler工具,基于16/14 nm工艺条件,对FREC部件的Verilog设计代码进行了逻辑综合,包括硬件支持非规格化浮点数的改进版(FREC2)。逻辑综合的约束条件相同,时钟频率均为1.6 GHz,两个版本均能满足频率设计目标,但是改进版有一定的面积和功耗开销,综合结果参见表3。 表3 逻辑综合结果Tab.3 Logic synthesis result 增加的面积主要为:源操作数预规格化中头零检测和左移移位器,结果后规格化中的右移移位器。增加的面积开销在合理范围内,主要是对时序没有影响,可以满足频率设计目标。 基于SRT-4算法,本文设计并实现了一种流水的FREC部件,6级流水线,支持浮点倒数流水运算,结果精度至少8位有效尾数。基于该部件,利用流水的快速浮点乘法运算,软件基于Newton-Raphson算法和Goldschmidt算法,可以更高效地流水实现任意精度的浮点除法运算等其他运算。这种方法尤其适用于低精度浮点运算应用。 本文还设计并实现了改进版的FREC部件,增加源操作数预规格化和结果后规格化功能模块,可以实现对浮点非规格化浮点数的硬件处理,有利于进一步提高浮点倒数近似值运算的性能。改进版的FREC部件采用8级流水线结构,由于支持流水操作,增加了2级流水线对运算性能的影响很小。经过逻辑综合评估,改进版的FREC部件硬件开销是面积增加19.23%。增加的面积开销在合理范围内,且对时序没有明显影响,可以满足预期的1.6 GHz频率设计目标。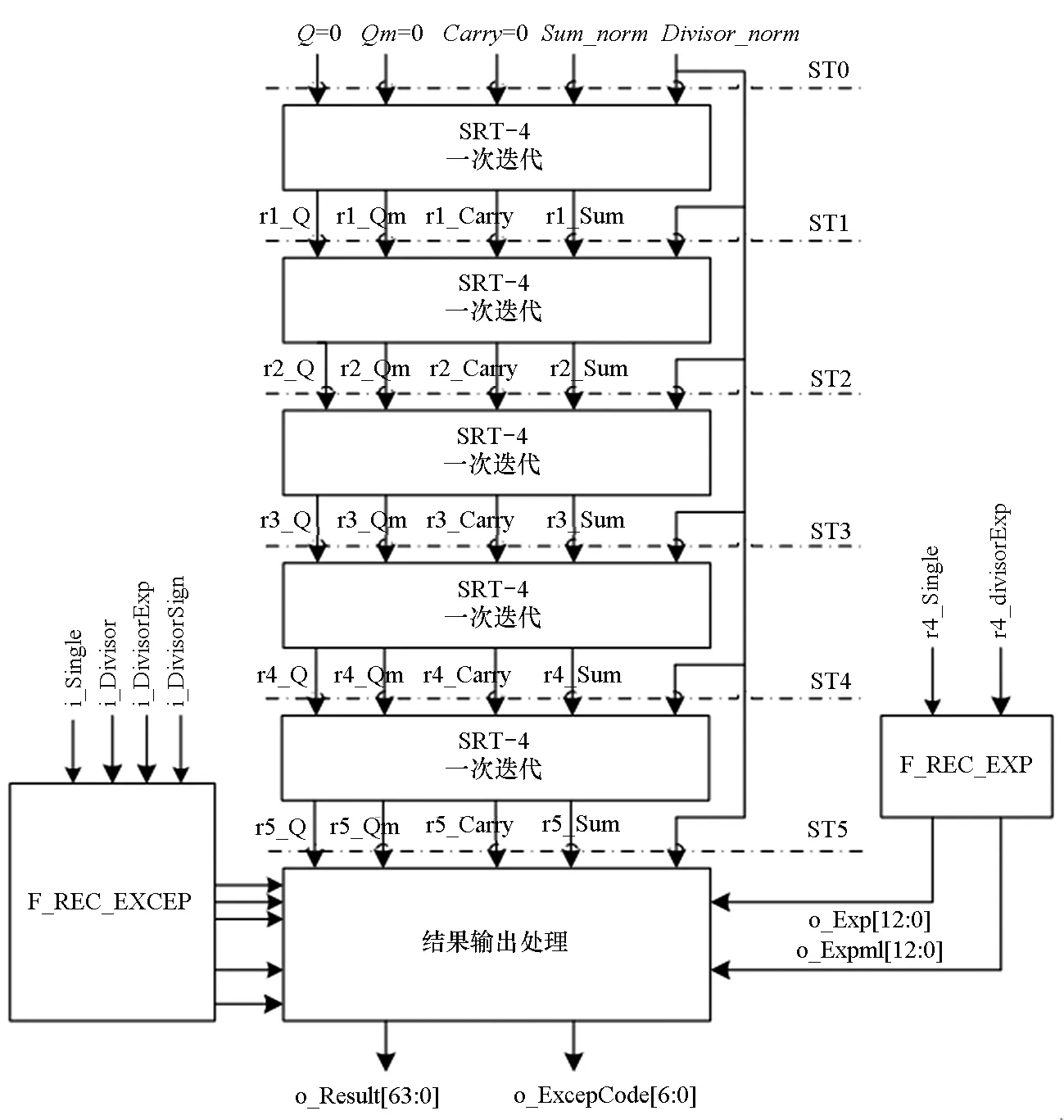


2 正确性验证与逻辑综合

3 结论

