薄带钢轧制环境下的轧机振动特性研究

王海博，杨彦涛

（黄河水利职业技术学院，河南 开封 475004）

0 引言

当前，我国钢铁企业产能普遍过剩，其中一些企业生产经营困难。 但是，一些高附加值钢材，如热轧薄板等，仍需要从国外进口。 因此，国内钢铁企业转型升级，迈入生产高端钢材领域迫在眉睫［1-2］。 国内某钢铁企业在生产薄带钢（厚度小于2 mm）时，第二架精轧机（简称F2 轧机）振动异常剧烈，致使轧机机架、主传动系统和液压管道剧烈振动，造成电机端子箱接头松动、螺栓断裂等故障，且产品上出现明暗相间的条纹，严重时甚至出现断带现象，导致生产中断，给企业造成较大经济损失。 针对这一问题，厂家现场采取了一些减振措施，但效果都不理想。 因此，有必要对F2 轧机的振动问题进行系统研究。

近年来， 国内外研究人员针对轧机振动做了许多有益的探索。例如：高亚南等人通过对轧机系统的扭振、垂振及水平振动信号的分析，发现工作辊轴承座衬板和机架衬板间隙过大是造成轧机振动的原因［3］。 和东平等人通过建立两自由度垂直非线性参激振动模型， 分析了非线性刚度系数和非线性阻尼系数等对振动的影响［4］。 轧机振动是涉及扭垂耦合、机电耦合和机液耦合的多态耦合振动，利用传统理论计算方法难以进行综合分析［5-6］。笔者试通过建立轧机系统的垂直振动和水平振动的有限元综合模型，求解多阶固有频率，并结合现场信号测试数据，查找导致轧机剧烈振动的优势频率， 以期找到造成轧机剧烈振动的原因，并探讨相应的减振措施。

1 轧机系统固有振动特性的有限元分析

轧机系统是由多系统组成的耦合系统。 根据轧机轧制时的振动特点， 可将轧机系统分为垂直系统和水平系统［7］。 本文根据厂方提供的轧机各部分零件图，利用PROE 软件建立三维实体模型。 对小的凸台、倒角、圆角等特征进行合理简化后， 利用PROE 提供的assembly 组装模块， 将各个部件按照实际情况进行组装，并将组装好的模型保存成iges 标准接口格式。 然后， 利用ANSYS 提供的import 接口将模型读入到ANSYS 软件中，确保装配体特征保持良好，无缺失。最后， 借助ANSYS 软件先进的模态分析算法和强大的处理能力，建立轧机垂直系统和水平系统的计算模型。

1.1 轧机垂直振动系统固有特性分析

轧机垂直振动系统主要由轧机牌坊， 液压压下装置，上、下支承辊，上、下工作辊组成，其三维实体模型和有限元模型如图1 和图2 所示。

利用有限元软件强大的求解器， 计算了轧机垂直系统的多阶固有频率，其中前10 阶的固有频率［8-9］如表1 所示。

1.2 轧机水平振动系统固有特性分析

轧机水平振动系统主要包括电机，联轴器，减速器，传动轴，齿轮座，上、下万向节轴，上、下工作辊等，其有限元模型如图3 所示。 振动发生时，轧机水平振动系统主要表现为扭转振动。

利用有限元软件解出轧机水平振动系统的前10 阶固有频率，如表2 所示。

图1 轧机垂直系统实体模型Fig.1 Rolling mill vertical system entity model

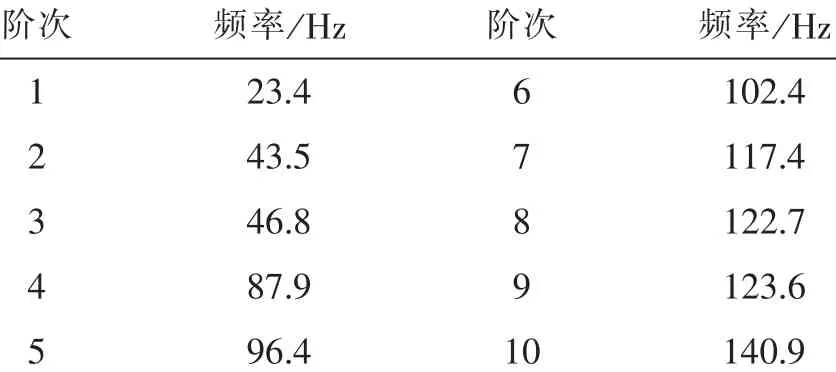
表1 轧机垂直系统前10 阶固有频率Tab.1 Natural frequencies of first ten phrase of rolling mill vertical system

图2 轧机垂直系统有限元模型Fig.2 Finite element model of rolling mill vertical system

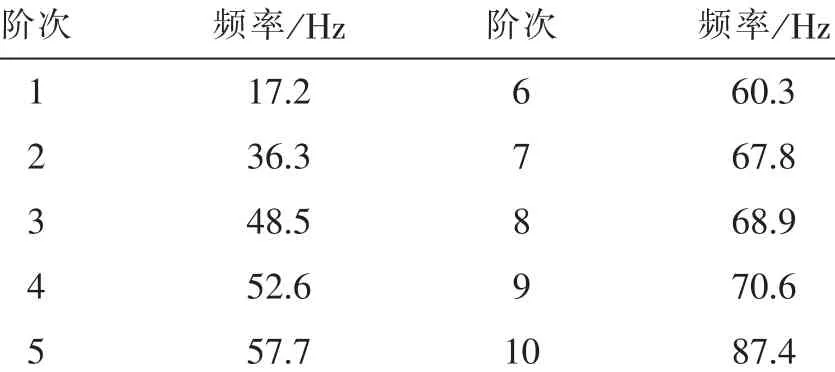
表2 轧机水平系统前10 阶固有频率Tab.2 Natural frequencies of first ten phrase of rolling mill horizontal system

图3 轧机水平振动系统的有限元模型Fig.3 Finite element model of rolling mill horizontal vibration system

2 轧机系统信号测试

2.1 测试方法

信号测试是处理设备故障常用的技术手段。 它通过安装在设备上的传感器， 采集设备在实际运行过程中的参数， 如力参数、 加速度参数和振动参数等，再通过降噪滤波方法，提取可以反映设备运行状态的数据［10］。结合轧机轧制过程的振动特征，本文采用加速度传感器采集振动数据， 采用电阻应变式传感器采集扭转振动数据。

2.2 测式参数

本次测试的主要参数有：机架振动加速度、齿轮分配箱及减速箱振动加速度、 轧制扭矩、 主电机电流、轧制力和转速等电参数，采样频率为1 000 Hz。主电机电流、轧制力、转速等工艺参数由电参数测试系统采集，采样频率为100 Hz。 传感器布点位置见图4 和图5。 各测点的位置、 方向等参数如表3 所示。 测试期间，设备主要参数如表4 所示。

图4 轧机垂直系统传感器布局简图Fig.4 Sensor layout of rolling mill vertical system

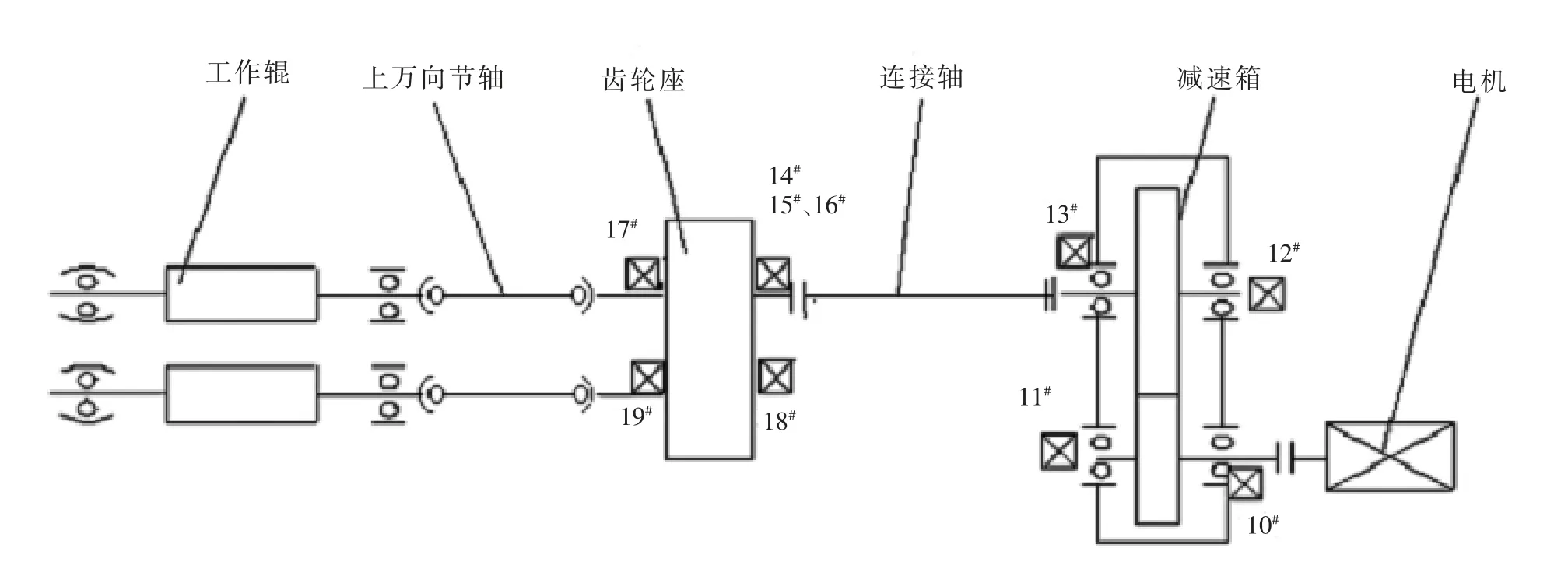
图5 轧机水平系统传感器布局简图Fig.5 Sensor layout of rolling mill horizontal system

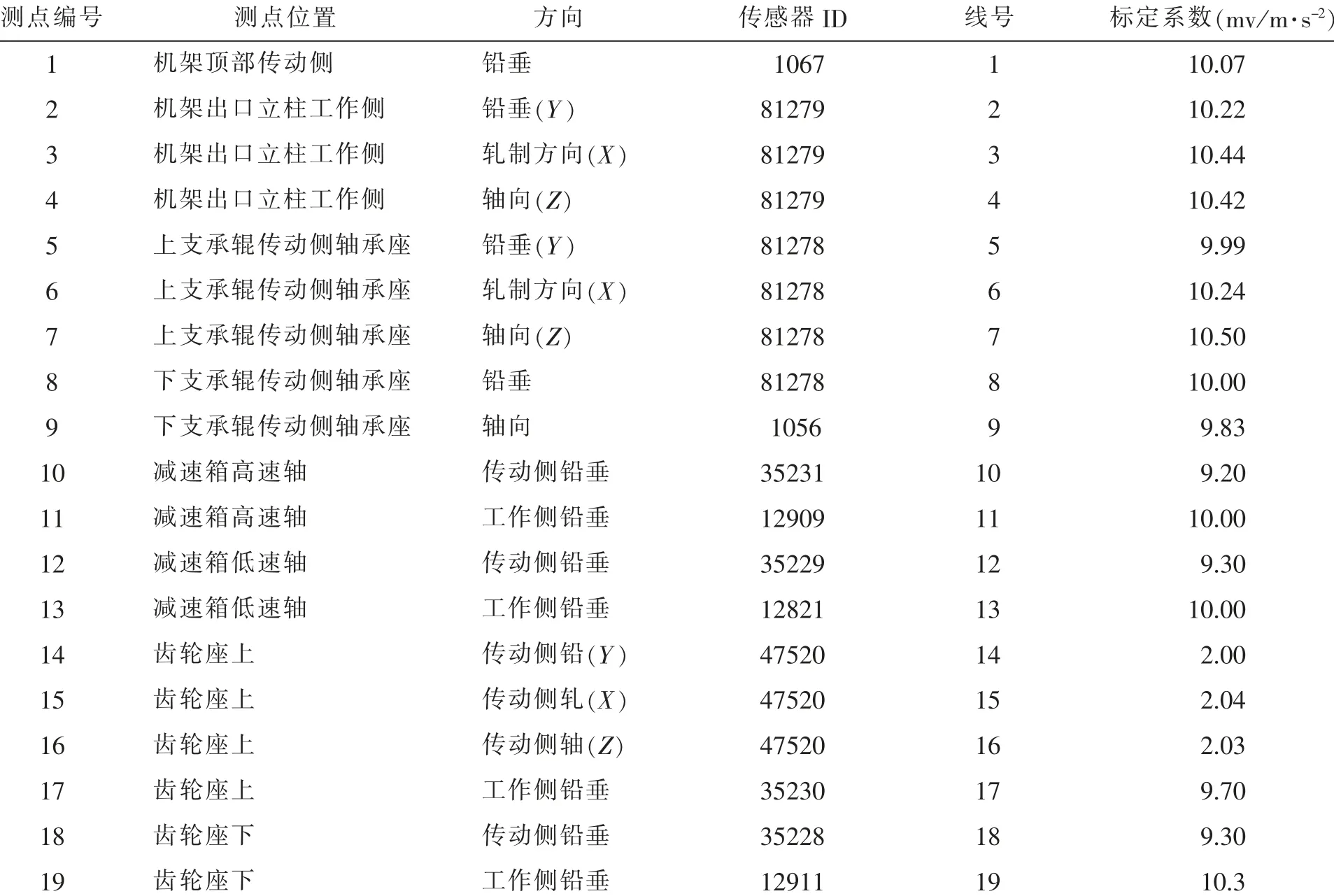
表3 F2 轧机现场测试传感器测点位置及标定Tab.3 Measuring point position and calibration of F2 rolling mill field test sensor

表4 测试期间设备主要参数Tab.4 Main parameters of equipment during test

3 测试结果分析

3.1 振源频率计算

轧机振动一般是由受迫振动和自激振动造成的。对于受迫振动，找到激振源是解决问题的关键。 本文采用频率比对法寻找振源。即将引起轧机系统剧烈振动的优势频率与可能的激励源频率比对，频率相近的振源就可能是激振源。 对于主传动系统而言，主要的激励源包括减速箱、齿轮座和弧形齿接手等。 这些振源频率及其倍频与电机转动频率存在线性关系。

3.2 轧机水平传动系统信号分析

对几组不同厚度钢板的扭转信号进行分析（传感器测点位于上万向节轴上），结果如图6 所示。

图6 轧制不同厚钢板时的扭矩时域图Fig.6 Torque time domain diagram of rolling different thickness steel

从图6 可以看出， 钢坯咬入瞬间产生的冲击对传动轴的扭振产生较大影响。钢板咬入后1 s 内，万向接轴的扭矩发生明显的扭转振动，且钢板越薄，振动越剧烈。 万向接轴的扭矩在钢板咬入瞬间达到峰值，然后下降，在稳态值附近波动（峰值远大于稳态值）。

将时域图转化到频域内，找出对应的优势频率。对比系统的激振源频率， 找到可能导致轧机剧烈振动的原因。 图7 是轧制不同厚度钢板时的扭矩信号在不同时段的频域图。

对图7 数据进行统计，结果如表5 所示。

上述信号的测点位于轧机主传动系统的上万向节轴上，可以反映主传动系统的特征。 从时域信号分析可以看出，轧机在轧制过程中，存在着明显的扭振现象。 从频域信号可以看出，主传动的优势频率集中在16.6～18.8 Hz。 由F2 轧机有限元固有频率分析可知，主传动系统的1 阶扭转固有频率为17.2 Hz。 轧制2.5 mm 及以下厚度板材时，扭矩的主要频率分布于扭振1 阶固有频率附近，在整个轧制过程中，始终存在着扭振现象。 轧制薄材时，电机初始转速约为90～110 rpm 时，齿轮座啮合频率为18 Hz 左右，这与主传动系统的1 阶扭振频率较为接近，易形成受迫振动。

3.3 轧机垂直系统测试信号分析

垂直系统信号测试的测点位于上支承辊传动侧轴承座上。 不同轧制钢板厚度的上支承辊轴承座在铅垂方向的时域信号及电机转速如图8 所示。

由图8 不同轧制厚度的时城信号分析结果可知，在轧制板材，特别是轧制薄材过程中，在一定时间段内，轧机存在剧烈振动，但剧烈振动发生的时间点并不固定，有时在咬入阶段，有时在中段，有时在尾部。 这表明，振动的发生具有随机性，发生的时间长短也具有随机性。这一现象是典型的自激振动，是由轧制界面摩擦条件改变所产生的［11-12］。 但是，振动也存在规律性。强烈自激振动发生时，对应的电机转速为110～120 rpm 和160～170 rpm，对应的减速箱和齿轮座啮合频率如表6 所示。

图7 轧制不同厚度钢板时的扭矩信号在不同时段频率图Fig.7 Different frequency chart of torque signal of rolling different thickness steel

表5 轧制不同厚度钢板时各时间段的频率Fig.5 Frequency of each component of rolling different thickness steel

由图8 可知， 当终轧板厚度大于2.5 mm 时，支承辊振动烈度相对较弱；当终轧板厚度小于2.5 mm时，振动烈度增强。 随着轧制界面摩擦状态的改变，还可能引起主传动系统的自激振动， 进而影响支承辊和机架的振动。

当电机转速达到110～120 rpm， 齿轮座啮合频率为21.4～23.3 Hz， 这与轧机第1 阶轴向振动频率23.4Hz 接近，易形成受迫振动。 随着转速的提高，齿轮座啮合频率逐渐远离垂直振动1 阶固有频率，剧烈振动现象逐渐消失。

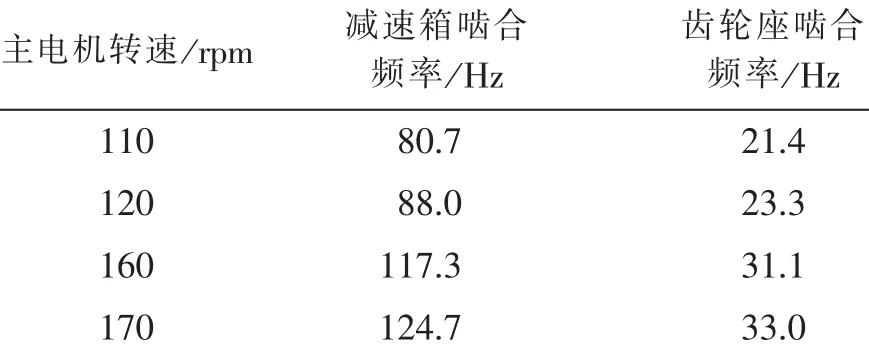
表6 减速箱和齿轮座啮合频率列表Tab.6 Meshing frequency list of gearbox and gear base

图8 不同轧制厚度的上支承辊轴承座在铅垂方向的时域信号及电机转速图Fig.8 Time domain signal and motor speed diagram of vertical direction of upper supporting roller bearing seat with different rolling thickness

4 结语

本文通过建立轧机系统的有限元模型， 计算出了轧机垂直系统和水平系统的多阶固有频率。 采用现代化的信号采集设备和技术， 对F2 轧机在轧制不同板厚带钢时的主要参数进行了全面综合测试，获得了大量准确可靠的数据。 选取上万向节轴上的扭转信号及上支承辊轴承座在铅垂方向的信号进行分析，并结合有限元模型的计算，得出以下结论：（1）机架及上、下支承辊自激振动发生时间具有随机性。轧制界面的摩擦状态不合理是造成严重自激振动的主要原因。 （2）轧机振动剧烈时，电机转速主要集中在90～110 rpm 和110～120 rpm 两个区间。 通过转速比和齿数与电机转速的换算， 对应的齿轮座啮合频率分别为16.6～18.8 Hz 和21.4～23.3 Hz。 （3）主传动系统的1 阶扭转固有频率为17.2 Hz，轧机垂直振动系统的第1 阶固有频率为23.4 Hz。这两组频率较为接近，易形成受迫振动。 当转速提高时，齿轮座啮合频率逐渐远离固有频率时，受迫振动现象逐渐消失。在轧机电机提速过程中， 通过控制电机快速通过上述区域，可以明显减轻轧机振动。