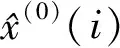深部持续采动诱发断层活化滑移的灰色预测研究

郭延辉 侯克鹏 杨 阳

(1.云南农业大学 建筑工程学院，昆明 650201；2.昆明理工大学 国土资源工程学院，昆明 650093)

随着国家经济建设的发展，对矿产资源需求的不断增加，使得矿山开采强度不断增大，越来越多矿山进入深部开采阶段，而深部岩体地应力较大，地质条件复杂，深部持续采动影响下断层活化，引发的冲击地压、岩爆等矿岩动力灾害日益严重[1]。如何针对开采诱发的断层活化开展监测，并对由其引发的灾害进行预测一直是科研人员关注的重要问题[2-3]。针对采动诱发断层活化滑移方面，国内外学者开展了大量卓有成效的研究，文献[4]通过二维相似模型实验，研究了工作面向断层推进过程中断层的活化滑移规律。文献[5]以断层带、上盘和下盘为系统，通过解析研究系统的稳定性，结果表明系统有2个应力比状态量，它们是断层面垂直应力、裂隙流体压力、内摩擦角及黏结力等系统参量的函数。文献[6]采用库伦破裂应力增量为断层活化判据，引入损伤因子评价断层面活化滑移破坏程度，探究了主应力偏转对不同倾角断层面上应力分布及断层滑移量的影响。现有研究成果主要是从采动影响下断层活化的规律与机理为出发点进行研究，而对于深部持续开采影响下断层活化滑移量的预测方面研究鲜有报道[7]。本文以某铜矿深部持续开采诱发F2断层活化滑移为背景，基于该断层3年多的实测数据，建立GM(1，1)灰色预测模型，对其未来一定时间段的活化滑移量进行预测，研究深部持续开采下断层活化滑移的灰色预测方法，以期为该断层的活化滑移量的预测提供参考。

1 灰色预测建模原理

1.1 GM(1，1)建模原理[7-8]

设有等间隔观测数列为：

X(0)(t)=

{x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)}

(1)

它对应的时间列为：t={t1,t2,…,tn}

将原始数据进行一次累加，生成新的时间序列为：

X(1)(K)=

{x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}

(2)

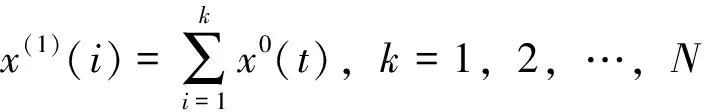
则X(1)(K)的GM(1，1)模型白化形式的微分方程为；

(3)

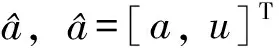
(4)

式(4)中：

通过计算得到X(1)的灰色预测GM(1，1)的时间响应函数：

(5)

对式(5)还原模型，便得到时间序列的预测模型：

(6)

1.2 灰色系统模型精度检验

1)模型检验[8-9]

灰色GM(1，1)模型构建后，需要对模型的预测精度及其可靠性进行检验，对评价标准进行验证。关联分析法和后验差检验法是最常用的检验方法。

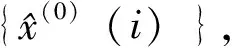
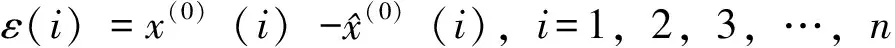
(7)

令S1为原始数据的均方差，S2为残差的均方差，则：

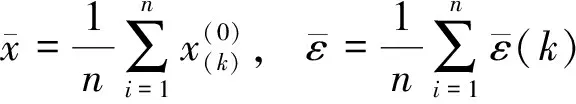
后验差检验指标为：

(1)后验差比值CC=S2/S1

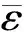
根据后验差比值C和小误差概率P确定的精度检验标准见表1。

表1 模型精度检验指标Table 1 Model accuracy test index

一般若P值越大，σ(k)、e(k)、C值越小，则灰色预测模型的精度便越好，反之模型的预测精度则越低。若灰色预测模型的精度不够，当误差较大的时候，则需对残差进一步处理。

2 深部持续采动诱发断层活化滑移分析

某铜矿位于云南省易门县，矿体主要分为主矿体，飘带矿，板岩矿。矿区共分为24个中段，每个中段高度50 m，采用崩落法开采，矿区主要开拓系统均布置于主矿体下盘。由于主矿体下盘受断层控制明显，下盘已揭露的主要断层有F2断层，F3断层，F4断层。根据断层实际活化滑移规律以及潜在滑移趋势，在主矿体下盘布置了断层活化滑移监测系统。主要对该矿区主矿体下盘10中段至14中段工程揭露的断层活化滑移规律进行监测。2010年4月，经现场实际调查，发现F2断层受深部持续采动影响下，已发生活化，并产生滑移，巷道揭露的地方，F2断层最大滑移量达0.50 m。巷道及硐室在F2断层滑移错动影响下，出现严重变形和破坏，位于断层上盘一侧的巷道、硐室及其它工程随着断层上盘一起整体下沉，断层上盘的很多开拓、采准工程废弃，无法继续使用。且随着15中段及以下矿体的深部持续开采，断层的活化滑移量持续增加[3]。图1为12中段大巷F2断层出现的活化滑移图。

图1 12中段大巷F2断层出现的滑动Fig.1 Activation slip diagram of F2 fault in the middle section 12

3 深部持续采动诱发断层活化滑移的灰色预测

深部持续采动影响下断层活化滑移的过程十分复杂，受到诸多因素的综合影响。在整个断层活化滑移的系统中，各因素的影响程度或贡献率(权重)很难确定。因此，深部持续采动影响下的断层的活化滑移问题具有很强的复杂性和非线性特征，既包含已知信息，也包含未知或非确知的信息，因此深部持续采动影响下断层的滑移过程可作为一个灰色系统来进行分析。

以该铜矿主矿体下盘F2断层BZX1号测点实测断层滑移量为例，构建灰色预测GM(1，1)模型，计算相关参数，并求解时间响应模型。将GM(1，1)模型的时间间隔设为三个月，取从2012年第1个三个月至2015年第13个三个月的13个实测数据进行研究，其时间序列为：

x(0)(t)={1个三个月，2个三个月，…，13个三个月}

={702，745，753，851，864，904，957，981，1 011，1 093，1 208，1 259，1 451}

对x(0)(t)进行累加，得到x(1)(k)序列：

即得到x(1)(k)序列：

x(1)(k)=[702，1 447，2 200，3 051，3 915，4 819，5 776，6 757，7 768，8 861，10 069，11 328，12 779]

YN=[x(0)(2),x(0)(3),…，x(0)(13)]T

=[745, 753, 851, 864, 904, 957, 981, 1 011, 1 093, 1 208, 1 259, 1 451]T

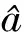
即a=-0.058 3，u=658.576 6

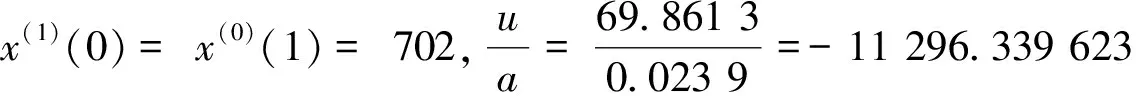
其时间的响应函数为：

=11 998.339 623e0.058 3 k-

11 296.339 623

还原模型：

=699.503 2e0.058 3 k

利用模型进行预测，监测值与预测值对比见表2所示。

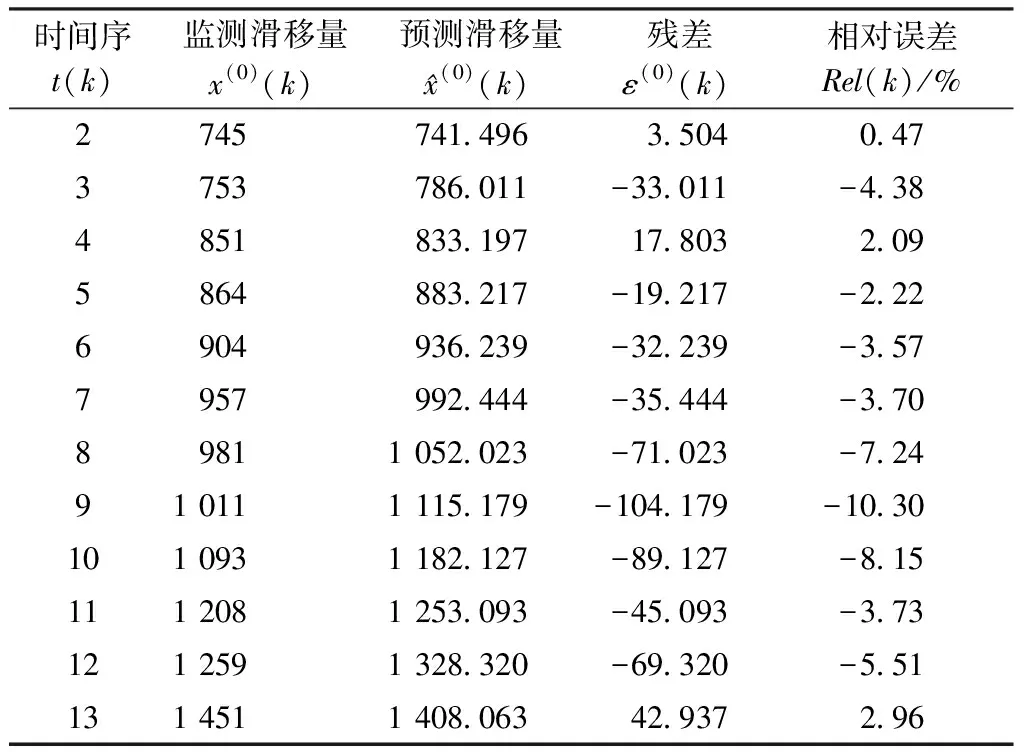
表2 模型预测值与实测值对比结果Table 2 Comparison results between predicted value and measured value of the model

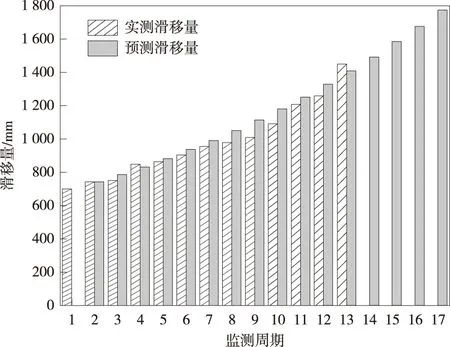
图2 断层滑移量预测值与监测值对比图Fig.2 Comparison between predicted value and monitored value of fault slip

4 结论