一种基于航天器通用下行信号相关处理的干涉测量方法及验证

路伟涛，陈 略*，任天鹏，韩松涛

(1. 北京航天飞行控制中心，北京100094； 2. 航天飞行动力学技术重点实验室，北京100094)

1 引言

甚长基线干涉测量技术(Very Long Baseline Interferometry， VLBI)通过高精度时延/时延率估计，实现探测器高精度角位置测量，与传统的测距、测速信息结合显著提高了深空探测器定轨精度，在深空探测任务中发挥了重要作用[1-2]。

自20 世纪70 年代，美国就将干涉测量技术应用于深空探测中，且测角精度从1993 年火星观察者号(MARS Observer)试验中的20 nrad，提高到2002 年的Odyssey 火星探测任务中的1 nrad量级，目前测角精度更是达到0.1 nrad 量级[3]。日本将同波束干涉测量技术(Same Beam Interferometry，SBI)应用于探月任务，实现了ps 量级的时延估计精度和10 m 量级的子卫星定轨精度[4-5]。中国探月工程中的干涉时延测量精度约1 ns，有力支撑了深空探测器的测定轨任务[6]。

根据CCSDS 标准[7]，深空干涉测量一般通过搭载VLBI 信标机实现，其中S 频段设置1 组信标信号(带宽约7 MHz)， X 频段设置2 组信标信号(带宽约40 MHz)。 国内外针对VLBI 信标体制下的干涉测量数据处理开展了大量的研究，Wu等[8]通过增加VLBI 信号处理带宽提高干涉测量精度；郝万宏等[9]引入锁相环处理，通过改善信号相位估计精度以提高干涉测量精度；马茂莉等[10]利用本地相关处理方法，提高相关处理频谱分辨率，改善干涉测量精度。

考虑到在轨航天器存在未搭载VLBI 信标机的情况，同时存在受航天器载荷限制无法搭载VLBI 信标机的问题，本文提出一种利用通用下行信号(遥测信号、数传信号等)开展干涉测量的相关处理方法，并根据通用下行信号载波抑制的特点，提出基于载波重建的相时延提取方法，针对某地球同步卫星下行信号特点，对所提出的数据处理方法进行试验验证。

2 干涉测量基本原理

干涉测量通过对接收信号进行相关处理，求取目标到不同测站的差分时延得到目标方向角估计，以此对深空探测航天器提供较强的横向约束，提高导航定位精度。 干涉测量原理如图1 所示。 设基线长度(两站天线相位中心的距离)为B、几何时延τ、几何路径差ΔR 及方向角θ，可得式(1)。

图1 干涉测量测角原理图Fig.1 Angle measurement scheme of interferometry

其中，c 为光速。 干涉测量时延估计精度直接受信号带宽影响，当信号带宽约40 MHz 时，时延估计精度可达到亚ns 级。 由式(1)可得到目标方向角估计θ＾，见式(2)。

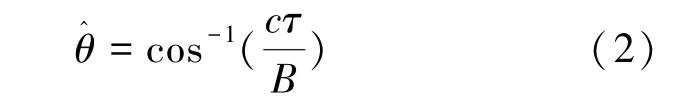
3 通用信号相关处理技术分析

3.1 通用下行信号载波重建

VLBI 信标信号可建模为正弦信号，且未调制其他数据。 而航天器通用下行信号，特别是宽带信号(如数传信号)一般通过编码和调制抑制了载波信息，以更有效地利用下行功率。 因此，为利用下行载波信息进行干涉测量，必须进行载波重建[11-12]。

假设两测站接收通用信号建模如式(3)所示。

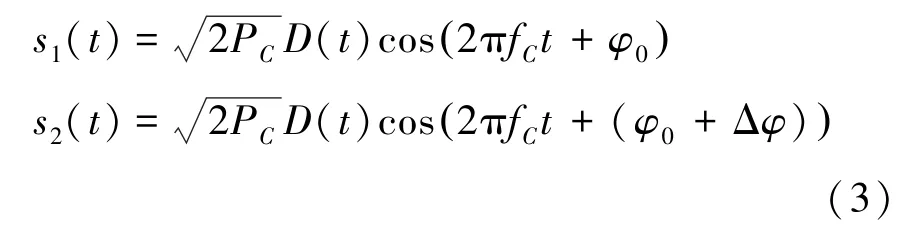
其中，PC为下行信号功率；D(t)为调制数据；fc为下行信号载波频率，φ0为信号初始相位，Δφ 为两站初始相位差。 载波重建目的即为提取Δφ。

文献[13]采用平方法实现了抑制载波调制的差分相位提取，主要处理过程包括群时延估计、时延补偿、平方法载波重建和差分相位估计，并分析了载波差分相位无模糊估计的时延补偿精度，见式(4)。

其中，T 为观测数据的中频载波周期， στ为时延测量精度。 实际信号处理一般在中频进行，中频采样率往往小于信号的载波频率，同时数据采集过程中的下变频处理不影响信号相位，因此，对于2.2 GHz的信号，假如下变频后中频频率为70 MHz，以56 MHz 欠采样，那么采样数据的中心频率在14 MHz左右，则群时延估计精度达到约6 ns时即可无模糊地提取式(3)中信号的差分相位。

3.2 载波相位整周模糊解算

干涉测量时延分为群时延和载波相位时延。其中，群时延由两测站接收信号直接相关处理和互谱相位拟合得到，时延测量范围大，精度受信号带宽约束，是当前深空探测任务中主用的干涉测量观测量，具体实现方式可参见文献[14]；载波相位时延是在高精度时延补偿的基础上，求解得到两测站载波差分相位以及相应的时延，时延估计精度与射频频率相关，较群时延精度高2 ～3 个量级，但需进行载波相位整周解模糊。 设载波差分相位为式(5)：

其中，Δφ 为真实载波相位差(即包含整周部分)； ΔN 为整周数差；Δφ 为非整周部分相位差。通常情况下，对VLBI 信标信号进行相关处理，可得到群时延估计，然后由群时延估计Δτg可以得到ΔN 的估计，即式(6)：

其中，[]表示取最近的整数，TC为fc载波的周期。 为了能够正确解整周模糊， Δτg的估计精度必须满足一定的要求。 本文采用3σ 准则，即式(7)：

其中，σΔτg为Δτg的标准差，此时通过群时延解算载波整周模糊的概率理论上为99.7%。 对于S 频段(2.2 GHz)的信号，解模糊要求群时延的估计精度为75.7576 ps。

3.3 系统时延偏差估计

选择经长期观测、位置精确已知的射电源进行系统时延偏差估计，是干涉测量中的常用方式[15-16]，具体方案如图2 所示。 其中，θ1、θ2为航天器T 和参考源S 相对两天线的夹角，夹角越小，差分标校效果越好。

图2 系统时延偏差估计方案示意图Fig.2 Estimation scheme of systematic delay bias

首先对参考源进行观测和相关处理，得到参考源S 到测站A、B 的时延估计τSA、τSB。 由于参考源位置和测站位置精确已知，可以通过计算得到参考源到两测站的几何时延差τSGeo，则由参考源的时延估计和几何时延差可以估计出测控系统的时延偏差，见式(8)：

设高轨卫星T 到测站A、B 的时延估计τTA、τTB，由上述系统时延偏差可以对高轨卫星的测量结果进行校准，见式(9)：

4 试验方案与结果

4.1 试验方案

为了验证通用信号干涉测量性能，试验方案流程如图3 所示。

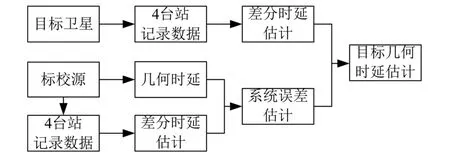
图3 通用下行信号干涉测量试验流程图Fig.3 Flowchart of interferometry test by using universal downlink signals

该方案包括以下4 个步骤：

1)选取观测目标。 本试验选择下行信号含有遥测和数传信号的某同步卫星，且得到其轨道信息，通过将干涉测量结果与已知轨道进行比对考查干涉测量的有效性。

2)目标差分时延估计。 对记录的中频信号进行差分相位提取、载波整周模糊解算等处理得到载波差分时延估计；

3)系统时延偏差估计。 由于测量系统往往存在一定的系统时延，使得载波差分时延估计值与实际几何时延存在偏差，因此必须进行系统时延偏差估计；选择某射电源进行差分观测，得到差分时延估计，并计算该射电源的几何时延，继而得到系统时延偏差估计。

4)测量精度验证。 将系统时延偏差估计与载波差分时延估计综合处理可得几何差分时延估计。 假设观测目标的轨道精确已知，那么可计算出观测目标到测站的精确几何时延，与几何差分时延估计进行对比，以评估干涉测量性能。

4.2 同步卫星通用下行信号载波时延提取方法

图4 给出了所选同步卫星数据的频域信息。可以看出，频谱显示数据含有2 种信号类型，分别为宽带数传信号和遥测信号，其中宽带数传信号主瓣位于16～25 MHz 之间，带宽约为9 MHz；经放大后，遥测载波位于3.143 MHz，带宽约260 kHz。

由于宽带数传信号群时延估计精度和遥测信号群时延估计精度均不能达到载波时延解模糊要求，故需要对2 种信号进行联合处理，处理框图如图5 所示。 首先对宽带数传信号进行相关处理，得到宽带群时延估计；然后从宽带数传信号和遥测信号中提取载波( 间距约17.4202 MHz)，求解两者的差分相位，并用宽带群时延进行解模糊，得到宽带-遥测信号的联合群时延；最后，考虑到宽带信号载波提取中平方损耗的影响，选择对遥测信号载波时延进行整周模糊解算，得到载波时延估计。

图4 某地球同步卫星数据频域信息Fig.4 Downlink signal spectrum of some GEO satellite

图5 基于双测控信号联合处理的载波时延估计框图Fig.5 Phase delay estimation based on joint processing of two types of downlink signals

上述方案存在二次解模糊过程：宽带群时延解算宽带-遥测联合群时延模糊、宽带-遥测联合群时延解算载波时延模糊。 解模糊对二次群时延估计精度的要求也不同。 设载波频率为fc，载波周期为Tc，采样频率为fs，采样周期为Ts，宽带群时延估计精度为στ1，宽窄带侧音群时延估计精度为στ2。 若补偿精度为整数比特，则二次群时延估计精度满足式(10)。

当采样率为56 MHz，载波频率约为2250 MHz，数传信号载波-遥测信号载波间距约为17.4 MHz，则两次群时延估计精度要求分别为2.98 ns 和72.46 ps。 可为积分时间的设定提供依据。

4.3 试验结果及分析

利用北京航天工程大学的天线组阵系统开展观测试验，该系统由4 个12 m 天线(测站)、1 个设备机房(数据处理中心)和1 个监控机房组成；4 个测站均通过同轴电缆与数据处理中心连接，干涉基线为百米量级[17]。 观测某同步卫星发射的遥测信号和宽带数传信号，观测时长约120 s。数据射频频率221x.xxxx MHz、中频频率70 MHz，中频采样频率56 MHz。

分段读取数据，每段数据长149.8 ms，间隔0.2 s，共读取80 段数据，时间跨度约16 s。 按照图5 流程处理。 由于宽带信号载波提取中平方处理会引起相位模糊，所以在相位提取过程中，通过宽带群时延估计结果对2 路信号进行补偿，使两者相位尽量靠近。

图6 给出了宽带群时延估计、补偿值。 其中时延补偿值精确到宽带群时延估计值整数位。 此处为34 Ts(Ts 为采样周期)；时延补偿后，2 路信号的残留时延均值约为2.9494 ns(约0.1652 Ts)。 由于时延补偿后，残留时延均值位于宽带侧音群时延的无模糊范围(约57.4046 ns)内，所以宽带侧音群时延不会出现整周模糊，符合图5 所示方案的解模糊要求。

图6 时延补偿结果Fig.6 Results of time delay compensation

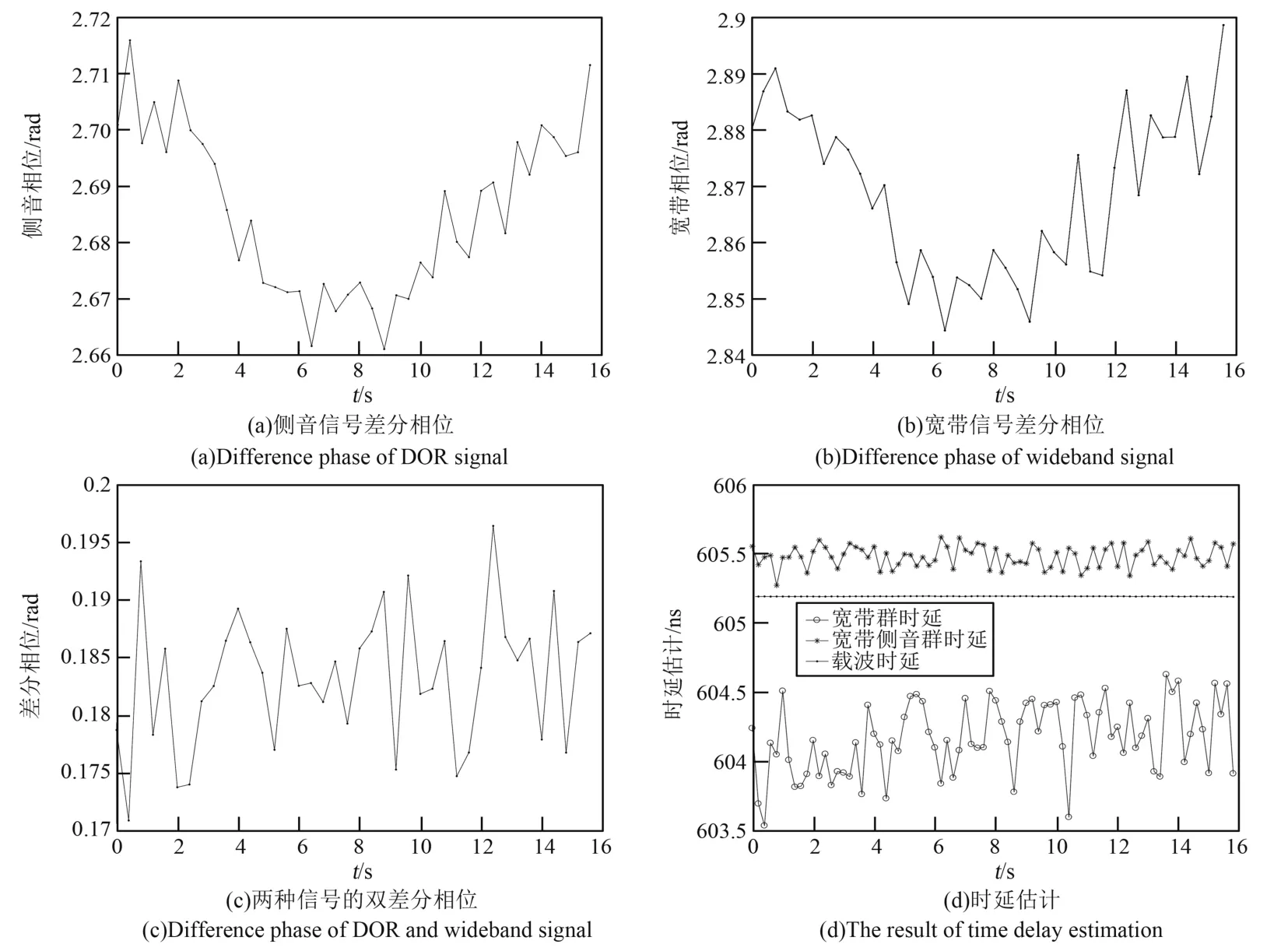
图7 信号差分相位与载波时延估计Fig.7 Results of differential phase and carrier phase delay

图7 给出了时延补偿后2 路信号的差分相位和时延估计结果。 图7(a)分别为遥测信号载波差分相位、宽带提取载波差分相位以及两者的差分相位。 可以看出侧音差分相位与宽带载波差分相位的趋势基本一致，两者的差分相位比较平稳，此时两者差分相位估计标准差为8.46 mrad。 图7(b)给出了宽带信号群时延、宽带信号载波与侧音信号载波群时延，以及估计出的载波时延结果，3 种情况估计均值与标准差分别为：604.1745 ns/256.1463 ps、605.4789 ns/77.2970 ps、605.1930 ns/1.0278 ps。

采样频率设置如前。 选择100 段数据，每段数据长度0.1498 s，两段数据间隔1 s，得到处理结果如图8 所示。 由图8(a)可以看出时延估计值与几何时延存在较大的偏差，但有相近的趋势。 将几何时延值与时延估计值相减，得到图8(b)，发现两者偏差的变化趋势减弱，以此作为系统时延偏差的估计，得到偏差均值为118.34 ns，标准差为0.92 ns。 所以系统偏差估计为118.34 ns。 以此对载波时延估计结果进行修正，并与几何时延进行对比，如图9 所示。 可以看出，两者趋势存在一定的差异，这是由于载波时延测量结果不够精确或数据质量不够高造成。 将估计值与几何值进行差分，得到差分时延均值为0.5967 ns、误差为1.03 ps。

图8 时延估计值相对几何时延的偏差Fig.8 Delay bias between time delay estimation and geometric delay

图9 载波时延与几何时延对比Fig.9 Comparison of carrier phase delay and geometric delay

5 结论

干涉测量技术以其高精度测角观测量为航天器测定轨提供了良好的横向约束。 针对航天器未搭载干涉测量信标机的情况，本文提出的基于航天器通用下行信号相关处理的干涉测量方和针对地球同步卫星下行信号的递进解模糊方法，可得到ps 量级的时延估计精度，在航天器测定轨中有着较为广泛的应用前景。

参考文献(References）

[ 1] 朱新颖， 李春来， 张洪波. 深空探测VLBI 技术综述及我国的现状和发展[J]. 宇航学报，2010，31(8)：1893-1899.

Zhu X Y， Li C L， Zhang H B. A survey of VLBI technique for deep space exploration and trend in China current situation and development[J]. Journal of Astronautics，2010，31(8)：1893-1899. (in Chinese)

[ 2] 马茂莉， 郑为民， 黄逸丹， 等. 嫦娥三号探测器DOR 信号本地相关处理与定轨验证[J]. 中国科学(物理学，力学，天文学)， 2017， 47(2)：100-108.

Ma M L， Zheng W M， Huang Y D， et al. Local correlation and orbit determination for DOR signals in Chang’E-3[J].Scientia Sinica (Physica，Mechanica ＆ Astronomica)，2017，47(2)：100-108. (in Chinese)

[ 3] 唐歌实. 深空测控无线电测量技术[M]. 北京：国防工业出版社， 2012：81-83.

Tang G S. Radiometric Measuring Techniques for Deep Space Navigation [M]. Beijing： National Defense Industry Press，2012： 81-83. (in Chinese)

[ 4] Liu Q H， Kikuchi F， Matsumot K. Error analysis of samebeam differential VLBI technique using two SELENE satellite[J]. Advances in Space Research， 2007， 40(1)：51-57.

[ 5] Goossens S， Matsumoto K， Rowlands D D， et al. 0rbit determination of the SELENE satellites using multi-satellite data types and evaluation of SELENE gravity field models[J].Journal of Geodesy， 2011， 85(8)： 487-504.

[ 6] 韩松涛， 唐歌实， 曹建峰， 等. 面向CE3 号软着陆过程的深空网干涉测量技术[J]. 深空探测学报， 2015， 2(2)：120-124.

Han S T， Tang G S， Cao J F， et al. Application of interferometric tracking by China DSN in CE-3 soft landing[J]. Journal of Deep Space Exploration， 2015， 2(2)：120-124. (in Chinese)

[ 7 ] CCSDS 506.1-R-2. Delta-DOR raw data exchange format[R]. Washington DC， CCSDS， 2010.

[ 8] Wu W R， Wang G L， Jie D G. High-accuracy VLBI technique using △DOR signals[J]. Scientia Sinica Informationis，2013， 43(2)：185-196.

[ 9] 郝万宏， 陆明泉. 嫦娥三号落月段中欧联合测量弱信号相位估计[J]. 武汉大学学报(信息科学版)，2019，44(10)：1442-1448.

Hao W H，Lu M Q. Phase estimation for inter-agency interferometric tracking in Chang’E-3 powered descent flight [J].Geomatics and Information Science of Wuhan University，2019， 44(10)：1442-1448. (in Chinese)

[10] 马茂莉， 郑为民， 黄逸丹， 等. 嫦娥三号探测器DOR 信号本地相关处理与定轨验证[J]. 中国科学(物理学，力学，天文学)，2017， 47(2)：100-108.

Ma M L， Zheng W M， Huang Y D， et al. Local correlation and orbit determination for DOR signals in Chang’E-3[J].Scientia Sinica (Physica， Mechanica ＆ Astronomica)，2017，47(2)：100-108.(in Chinese)

[11] Viterbi A J，Viterbi A M. Non-linear estimation of PSK-modulated carrier phase with application to burst digital transmissions[J]. IEEE Transactions on Information Theory， 1983，29(5)：843-551.

[12] 王翠莲， 李寅， 禹霁阳， 等. 深空通信载波同步高精度FFT 频偏估计算法[J]. 航天器工程， 2018(6)：63-68.

Wang C L，Li Y，Yu Q Y，et al. High accuracy FFT frequency offset estimation carrier synchronization algorithm in deep space communication[J]. Spacecraft Engineering， 2018(6)：63-68. (in Chinese)

[13] 路伟涛， 洪家财， 杨文革. 基于宽带相处理的连线干涉测量[J]. 装备学院学报， 2014(2)：80-85.

Lu W T， Hong J C， Yang W G. Connected elements interferometry based on wideband correlation processing[J]. Journal of Equipment Academy， 2014(2)：80-85. (in Chinese)

[14] 钱志瀚， 李金岭. 甚长基线干涉测量技术在深空探测中的应用[M]. 北京： 中国科学技术出版社， 2012：58-76.

Qian Z H，Li J L. The Application of VLBI in Deep Space Exploration [M]. Beijing： Science and Technology of China Press， 2012：58-76.(in Chinese)

[15] 陈略， 唐歌实， 任天鹏， 等. 再入返回飞行试验深空网干涉测量应用分析[J]. 飞行器测控学报， 2015， 34(5)：407-413.

Chen L， Tang G S， Ren T P， et al. Application of CDSN interferometric tracking in reentry return flight test missions[J].Journal of Spacecraft TT ＆ C Technology，2015，34(5)：407-413. (in Chinese)

[16] Roberto M， Trevor M， Ricard A. Delta-DOR a new technique for ESA’s deep space navigation [J]. ESA Bulletin， 2006，(128)：69-74.

[17] Shi X S， Ma H， Jiao Y W. Optimizing deep-space antennas array configuration by multi-objective genetic algorithm[C]/ /Proceedings of the 27thConference of Spacecraft TT＆C Technology in China， Chengdu， 2015：151-160.