基于LSA模型的改进密度峰值算法的微学习单元文本聚类研究*
武国胜,张月琴
(太原理工大学信息与计算机学院,山西 晋中 030600)
1 引言
信息化时代及快节奏生活让社会进入到信息碎片化、作息时间碎片化的时代。为适应利用碎片化时间进行学习的需求,2005年微学习[1]的概念应运而生。作为一种新的在线学习方式,微学习和其他学习方式最大的不同,在于微学习资源广泛存在于网络上,MOOC、SNS等平台中的短文本、短视频、图片等都可以成为微学习资源,让学习者可以在短时间内进行学习。随着微学习这种新学习方式的出现,学习者不仅可以无处不在地学习,更可以利用碎片化时间进行学习。近年来,微学习获得了越来越多的学者的关注和研究,并取得了一定的研究成果[2]。但是,随着学习资源的日益丰富,同一学习内容的多源异构形式也给学习者带来了“学习迷航”和“信息过载”等问题,导致学习者很难在短时间里找到适合自己的学习资源。为此,实现对微学习资源的合理组织,对促进学习者的个性化学习具有重要意义。
聚类技术通过无人监督的方式广泛应用于发现信息间的隐藏关系。为了便于发现微学习资源间的隐藏关系,本文把微学习过程中最小的学习单元[3]——微学习单元作为研究对象。从微学习单元的构成形式来看,文本是重要形式之一,所以本文将尝试对文本形式的微学习单元进行聚类,以方便学习者甄别适合自己的学习资源。
文本聚类是文本挖掘的研究方向之一,其研究成果被广泛应用于信息检索。而语义分析处理等方面的研究成果也被用于改善文本聚类的效果。经过多年的发展,文本聚类取得了大量成果,但是微学习单元的聚类准确度还有进一步改善的空间。首先,目前传统的文本聚类方法使用向量空间模型VSM(Vector Space Model)[4],采用特征词及其权重构成向量表示文本。由于微学习单元文本信息具有短小、精炼且数量巨大的特点,文本特征向量表现出高维稀疏性,使得模型在表征微学习单元文本主题时容易失焦。其次,虽然文本聚类算法数量众多[5],但在微学习单元文本聚类方面表现不佳。例如,K-means算法[6]需要事先指定类别数,迭代过程中容易陷入局部最优;基于层次的算法[7,8]聚类过程中不可逆,合并终止条件对聚类结果影响较大。而基于密度的聚类算法[9,10]通过将关联紧密的样本划为一类,来获取不同聚类类别,可适用于凸样本集和非凸样本集,鉴于其适合的样本集较为广泛,故本文尝试利用基于密度的聚类算法来实现对微学习单元文本的聚类处理。作为一种基于密度的经典聚类算法DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[8],该算法具有不需预置聚类数量,能分辨噪声,可找出任何形状的聚类等优点。但同时也存在调参过程复杂的问题,如果未能充分把握数据的密度比例,将很难选择适合的参数。
2014年,Rodriguez等人[11]提出了密度峰值聚类CFSFDP(Clustering by Fast Search and Find of Density Peaks)算法。CFSFDP算法较DBSCAN算法拥有更多的优点,但在处理存在高维稀疏问题的向量空间数据时,也存在计算局部密度时没有统一的度量,选择欧氏距离作为度量会导致所表示的微学习单元数据缺乏全局性的问题,且截断距离(Cutoff Distance)的选择对聚类结果的影响较大。此外,密度中心的选择依赖于人工监督,在处理大规模数据时会影响算法效率和计算的准确率。为解决原有文本聚类算法在微学习单元文本聚类方面存在的上述问题,本文采用潜在语义分析LSA(Latent Semantic Analysis)模型[12]对微学习单元建模,并利用奇异值分解SVD(Singular Value Decomposition)方法对高维稀疏特征向量进行降维处理;然后通过密度敏感距离重定义密度计算方式,并改进密度峰值中心获取方法,使其更适用于微学习单元文本聚类。用人工和微学习真实数据集在Matlab中进行仿真实验,通过和原算法以及一些经典文本聚类算法进行比较发现,本文提出的微学习单元聚类算法更适用于微学习单元文本聚类。
2 相关工作
本节首先介绍与文本聚类相关的向量空间模型,然后介绍密度峰值聚类算法,最后对与密度聚类算法密切相关的参数密度敏感距离进行说明。
2.1 向量空间模型(VSM模型)
向量空间模型VSM是由Salton等人[4]在1969年提出的。该模型将文本内容转换为特征词及其权重构成的向量,在多维空间表示为1个点,使文本处理问题复杂度大幅降低。VSM模型表示文本的流程包括分词、停用词处理、词根处理以及权重计算等。模型中文本集D中存在M个特征词、N个文本,任一文本dj都可以表示成dj={(t1j,ω1j),(t2j,ω2j),…,(tMj,ωMj)}的形式,其中tij(i=1,2,…,M;j=1,2,…,N)为特征词,ωij(i=1,2,…,M;j=1,2,…,N)为特征词对应的权重。权重计算方法使用得较多的是由Salton等人[13]提出的词频及逆向文档频TF-IDF函数。
向量空间模型以其基于线性代数的简单模型,允许以文本间可能的相关性进行排序,以及对相似度进行连续取值,受到广泛青睐。不过,由于向量空间模型假定文本在统计上是独立的,即认为词与词之间是相互独立的,割裂了文本固有的语义关系,因此该模型处理微学习单元短文本时存在因特征不足而带来的严重稀疏性问题。
2.2 密度峰值聚类算法(CFSFDP)
Rodriguez等人[11]提出的CFSFDP算法基于2个简单直观的假设:(1)聚类中心的密度高于其邻居点的密度;(2)聚类中心与具有较高局部密度的任何点的距离都相对较远。根据这2个假设,CFSFDP算法首先需要确定2个参数:(1)局部密度;(2)与高密度点间的截断距离。并以此为依据把其他点分配到以潜在的密度峰值点为中心的聚类里。其中,局部密度为与当前数据点间的距离小于截断距离的数据点的个数。截断距离为聚类时的数据点到当前数据点的最大距离。该算法在计算数据点间的距离时采用欧氏距离。
文献[11]中使用大量实验证明了密度峰值算法对凸型和非凸型数据均具有良好的处理效果。但是,在针对微学习单元文本聚类的应用中发现,CFSFDP算法中计算局部密度和选取密度峰值中心的方法未能适应微学习数据的特点。
首先,CFSFDP算法使用的“截断距离”参数,采用取邻近的平均数据点数是总数据点数的1%~2%作为截断距离,该选择没有明确的选择依据。如图1所示,在不同截断距离下,聚类准确度和效果会出现差异。
图1表示在pathbased2数据集上选取不同截断距离进行实验的结果。图1a表示在截断距离选取不合适时的聚类结果,其类簇数变为4,出现错误。图1b表示选取截断距离合适的聚类结果,其正确的类簇数为3。
近年来许多学者也注意到了该不足,如Mehmood 等人[14]提出了一种利用热扩散的方法和核密度来重新定义密度,此方法可以自适应计算带宽,以不依赖任何参数的方式解决阶段距离敏感的问题。Xie等人[15]提出了一种使用模糊加权K-最近邻的方式来定义点的局部密度并搜索和发现聚类中心,只需要1个参数来解决CFSFDP算法密度测量不均的问题。Liu等人[16]引入共享近邻的概念重新设计了一种分配策略,可以快速搜索和找到密度峰值进行聚类。
其次,CFSFDP算法在选取密度峰值点时,采用人工监督的方式。在预先知道类簇数目的前提下绘制密度-距离决策图,并认为密度峰值点是局部密度和与高密度点之间的距离均较大的点,这些点在决策图中一般出现在所有数据点右上角的位置,且通过人为选出图中表现“突出”的已知类簇数目的数据点作为密度峰值点。这一选择方法在面对大量数据处理时难度大,会影响算法的准确度和执行效率。许多学者针对此问题取得了一些研究进展。Gao等人[17]设计了一种非视觉决策图,采用基于降序碰撞选择聚类中心的方法选取聚类中心。Liang 等人[18]利用DBSCAN框架中的分而治之和密度可达概念提出了自动选择聚类中心的策略,该策略可以以递归方式自动查找正确数量的簇。

Figure 1 Influence of different cutoff distances on clustering results图1 不同截断距离对聚类结果产生的影响
2.3 密度敏感距离
2007年,王玲等人[19]通过观察样本数据的空间分布情况,设计了一种简单有效的空间一致性距离测度:密度敏感距离。密度敏感距离测度可以度量沿着流形上的最短路径,从而实现了放大位于不同高密度区域上数据点间的距离,而缩短位于同一高密度区域内数据点间距离的目的。
密度敏感距离建立在密度可调节距离的基础之上,其思路是引入伸缩因子,并把欧氏距离作为伸缩因子的幂因子;然后通过调节伸缩因子的大小来增大或缩小2个数据点间的距离。
密度敏感距离则用于发现不同流形数据点上的最短路径,这使得位于同一高密度区域内的2点可以用较短的边相连接,而位于不同高密度区域内的2点要用较长的边相连接,从而实现了放大位于不同高密度区域上数据点间的距离,缩短位于同一高密度区域内数据点间距离的目的[20]。
2.4 潜在语意分析
潜在语义分析(LSA)模型最早由Deerwesster等人[12]提出,其原理为将高维向量空间通过奇异值分解SVD映射到低维的潜在语义空间,在扩展语义信息的同时达到降维去噪的目的[21]。
相比于VSM模型的独立性假设,LSA模型假设文本中词语间存在紧密的联系,构造M×N维特征词-文本矩阵来描述文本中词项的共现性,其中M表示文本集特征词个数,N表示文本集中文本个数。特征项A通常采用TF-IDF[12]向量计算权重。
对原始空间矩阵A做奇异值分解(SVD),如式(1)所示:
(1)
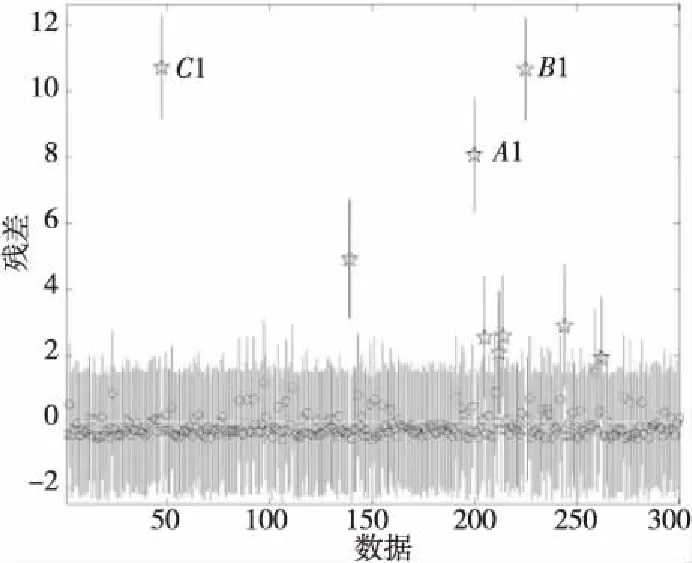
其中,矩阵UM×M为M×M的左奇异向量矩阵,存储了语义相关的词向量。矩阵VN×N为N×N的右奇异矩阵,存储了主题相关的文本向量。Σ=diag(σ1,σ2,…,σr)∈Rr×r是一个由A的特征值组成的r×r的对角阵,σ称为奇异值。奇异值按降序排列且前k(k< (2) 本文提出的微学习单元文本聚类算法由以下4部分组成:微学习单元分割和标记、微学习单元文本数据预处理、微学习单元特征提取、微学习单元聚类。该聚类方法的流程图如图2所示。 Figure 2 Process of proposed algorithm applied to micro-learning unit text clustering图2 本文算法应用于微学习单元文本聚类流程 第1部分微学习单元分割和标记是将获取的微学习文本资源中标题和描述作为数据处理对象,对其内容类别进行手工标注和分割,从而获取微学习单元。第2部分文本数据预处理阶段将标注的微学习单元文本数据进行文本的分词处理、停用词处理、词干提取。第3部分微学习单元特征提取对处理过的文本数据进行建模和特征降维,得到合适的文本特征向量。第3和第4部分构建模型及微学习单元聚类是本文研究的重点。 微学习单元是微学习过程中最小的学习单位,每个课程C由一系列微学习单元构成。假设微学习过程中存在n个课程,任意1个课程Ci(i=1,2,…,n)可以由m个微学习单元组成,即Ci={U1,U2,…,Um}。 在进行模型构建过程中,由于本文使用微学习单元的标题、描述和文本内容作为微学习单元的文本数据,故数据有着单一文本长度较短、文本特征词数据量少、文本数量较多的特点。若使用VSM模型(向量空间模型)建立微学习单元模型,会遇到微学习单元特征不足、特征词向量高维稀疏等问题。故本文选择采用潜在语义分析模型LSA进行微学习单元建模及特征降维工作。 在上述基础之上,本文对密度峰值算法在微学习单元文本聚类中存在的问题,提出2点改进。 首先,本文改进了数据点间距离计算时的度量方法,提出了自然指数型距离度量方法,以解决文献[19]中伸缩因子大于1时遇到的伸缩比例不易调整的问题。 定义1 基于密度峰值算法的自然指数型距离度量矩阵L如式(3)所示: L(xi,xj)=eρ×dij-1 (3) 其中,dij表示数据xi与xj之间的欧氏距离,ρ表示伸缩因子(ρ>0),ρ可用于调节数据点间的距离度量。使用指数型调节函数,并通过伸缩因子ρ在次幂上进行调节,这样可以使得调节的幅度得到合理的控制。 通过改进距离度量方法来引入密度敏感距离,将密度敏感距离作为微学习单元文本聚类的相似性度量,以此来改进CFSFDP算法对微学习单元文本聚类时遇到的全局一致性不足的缺陷,并通过该方法更好地寻找密度峰值中心。 定义2(数据点局部密度) 根据改进的自然指数型距离度量计算方法,并将其引入密度敏感矩阵中,即得到任意2个数据点xi,xj密度敏感距离矩阵S。 (4) 其中,p∈Vl表示图G中1个长度为l=|p|-1的连接点p1和p|p|的路径,且边(pk,pk+1)∈E(1≤k≤|p|-1),Pij表示xi与xj之间所有路径的集合,L(pk,pk+1)表示连接pk与pk+1之间基于密度峰值算法的自然指数型距离。采用Dijkstra[22]计算最短路径长度。 随后,将密度敏感距离作为相似性度量,重新定义不依赖于截断距离的局部密度公式。已知空间X={x1,x2,…,xi,…,xn}中对象xi的密度记作density(xi),如式(5)所示: (5) 该局部密度定义可以描述为数据点xi与其相连接的所有数据点间距离的比值之和。这样的密度定义方法降低了算法对截断距离取值的敏感性,并且可以反映数据的密度分布,和CFSFDP算法的密度计算方法相比,能更好地保持全局一致性,便于聚类分配时正确地分配微学习单元,提高文本聚类的效果。具体描述如算法1所示。 算法1 基于密度敏感距离重定义局部密度 输入:微学习单元文本子空间X={x1,x2,…,xn},伸缩因子ρ。 输出:数据点局部密度density(xi)。 步骤1 计算文本子空间X中各数据点间的欧氏距离,得到欧氏距离的矩阵D: D(xi,xj)=dij,1≤i≤n,1≤j≤n 步骤2 根据欧氏距离矩阵D用式(3)计算密度可调节线段长度,在ρ∈(0,3)调整伸缩因子,得到自然指数型距离度量矩阵L; 步骤3 将自然指数型距离度量矩阵L代入式(4),得到密度敏感距离矩阵S; 步骤4 将密度敏感距离矩阵代入式(5),得到每个数据点的局部密度density(xi) 步骤5 算法结束。 本文从CFSFDP算法选取密度峰值中心的原理出发,提出根据残差分析异常点,进而选取密度峰值的方法。如图3a和图3b所示,密度峰值点A、B、C与普通数据点距离较远,且处于右上方的位置(图3b)。如果尝试将ρ-δ组成的数据进行线性拟合,可发现该数据集密度峰值中心就是经过线性拟合后的那些最为偏离大部分数据的异常点——野值点。 线性回归是利用数理统计中的回归分析,来确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法[23]。即对于n个数据的数据集,ρ和δ拟合时的线性关系为:δi=f(ρi)=a+bρi,i=1,2,…,n。所以,当利用残差分析的方法对ρ-δ线性拟合以找出线性拟合过程中的奇异点时,如图4所示,其中,A1、B1、C1分别对应图3b中A、B、C3个密度峰值点的残差,奇异点包括密度峰值点,但奇异点不都是密度峰值点,这是因为密度峰值中心是那些ρ和δ均比较大的数据点,而有些数据点是ρ或δ其中1项较大,而另1项较小,这些点往往是远离类簇的点或类间点。本文算法的目标是去除这些点,而保留最为偏离大部分数据的点——野值点。所以,在进行线性拟合时,并不能1次性地选择出这些野值点作为正确的密度峰值中心。 Figure 3 Using density peak algorithm to find the peak center point law图3 密度峰值算法寻找峰值中心点规律 Figure 4 Analysis of outliers by residuals in Matlab图4 在Matlab中通过残差分析异常点 为选择出野值点,本文集中对使用残差法进行线性拟合时得到的参数进行分析。本文观察到野值点与其他奇异点在残差上存在较大不同,为此本文对残差分析后得到的残差加以约束,使用这个约束条件将野值点和其他奇异点分离,保留野值点,剔除其他的奇异点。保留的野值点由于ρ和δ均较大,而导致其进行线性拟合时成为奇异点,而密度峰值点是一些被低密度点包围且到其他高密度点的距离较大的点,为此这些野值点能够代表整个类作为类簇中心,即野值点就是密度峰值中心点。具体描述如下文所述: 假设密度峰值中心数据点下标为DPCDP(Density Peak Center Data Point),线性拟合过程中得到的数据点残差为ri,残差下限为rli,残差平均值为ra,残差的方差为rσ,则约束条件为: DPCDP={i|rli>0&&(ri-ra)>3×rσ} (6) 其中, (7) (8) 其中,约束条件中的数字3为实验得到的最佳约束参数。 使用这样的约束条件后,其他奇异点被剔除,剩下的就是经过线性拟合得到的野值点,而这些奇异点在数据集中表现为各类的密度峰值中心,下标点的个数即为密度峰值算法需要聚类的类簇数。如此,通过残差分析和条件约束可以避免CFSFDP算法中人工选择的不准确以及不够智能的缺陷,提高算法选择密度峰值中心的准确率以及算法运行效率。通过Matlab仿真实现改进的CFSFDP选取峰值中心的具体步骤如算法2所示。 算法2 自动选取密度峰值中心 输入:局部密度ρ,最近且密度比数据点大的点的距离δ。 输出:密度峰值中心数据点下标DPCDP。 步骤1 由局部密度ρ和距离δ绘制ρ-δ决策图; 步骤2 根据以ρ为横坐标、δ为纵坐标的数据点在Matlab上进行线性拟合,由Matlab自带的残差分析工具得到残差ri和残差下界rli; 步骤3 根据式(7)和式(8)计算残差平均值ra和残差的方差rσ; 步骤4 根据式(6)计算密度峰值中心数据点的下标,得到DPCDP; 步骤5 算法结束。 本次实验采用微学习单元的真实数据集,并和经典文本聚类算法以及CFSFDP算法进行对比实验,从而分析以得到最后的结论。对比的经典文本聚类算法是K-means算法[6]、DBSCAN算法[9]和DPC-KNN算法[24]。K-means算法是由Matlab自带的库函数进行测试工作的,DBSCAN算法是根据作者提供的源码进行测试和实验。DPC-KNN算法是一种采用K-最近邻方式避免截断距离敏感的算法,由于其性能近年来得到了广泛的关注,且该算法类簇分配策略与本文算法一致,便于进行对比,所以本文选择该算法进行对比实验。DPC-KNN算法按照文献[25]理论使用Matlab模拟。 本次实验使用的微学习真实数据集来自于网络平台。使用Python 2.7在Windows 10系统下,通过官方提供的Scrapy模块进行爬取。数据来源网站是 Coursera,Coursera是世界上三大MOOC平台之一,由于其课程免费,且课程数量较多,内容较为丰富,便于系统收集学习课件,所以选择该平台作为数据来源。最后,实验模拟使用的测试软件为Matlab R2016a ,实验环境是Intel Core i5, 8 GB内存,Windows 10操作系统。 在实验中采用聚类准确率(ACC)、调整互信息指数(AMI)[26]和调整兰德指数(ARI)[27]来评价聚类结果。 ACC指标定义如下: 其中,n是数据点的数量,yi和ci是真实标签和数据点xi的预测标签。当yi=ci时,δ(yi,ci)=1,否则为0。 ARI指标定义如下: AMI指标定义如下: 其中,U表示实际类别集合,V表示真实聚类类别集合,p(u)和p(v)分别为u和v的边缘概率密度函数,p(u,v)为联合概率密度函数。H(U)和H(V)为U和V的信息熵。 这3种度量指标取值上界均为1,值越接近1表示聚类结果越好。 按照本文聚类算法的4个组成部分,本次实验的步骤如下所示: (1)微学习单元分割和标记。选择课程平台中每个课程的课程名称及课程标题作为主要文本内容。课程提供平台并没有已存在的微学习单元,所以本文以周为分割周期将课程分割成微学习单元,每个课程由多个微学习单元组成,每个单元独立存在。为微学习单元标注4个属性,分别为微学习单元编号、微学习单元类别、微学习单元标题(Unit Title)和微学习单元描述(Unit Description)。部分微学习单元内容如表1所示,手工标注后的微学习单元所属类别和编号如表2所示。 (2)微学习单元文本数据预处理。数据预处理的操作包括:文本的分词处理、停用词处理、词干提取。本文使用Python NLTK[28]工具实现文本分词工作,通过设置停用词表的方式将停用词进行过滤处理,词干提取方法采用波特词干提取法[29]。 (3)微学习单元特征提取。经过预处理后的微学习单元数据需要进一步结构化表示,这样才能被计算机识别,从而通过计算机分析处理。这一过程的步骤包括:特征项的选择,特征项权重计算,LSA模型[12]表示微学习单元,相似度计算。经预处理得到特征维度为1 131维的稀疏特征词空间,采用TF-IDF算法[13]分别计算微学习单元的标题和单元内容描述这2个字段的特征词权重。最后通过LSA模型表示微学习单元数据,以便于计算机识别,本文k值选择100, Table 1 Partial micro-learning unit content表1 部分微学习单元内容 Table 2 Category and content of the micro-learning unit after manual labeling表2 手工标注微学习单元后的所属类别和内容 经SVD分解降维后得到低维语义空间,最后使用欧氏距离[25]计算相似度。 (4)使用本文提出的改进的密度峰值算法、K-means算法、DBSCAN算法和DPC-KNN算法在微学习单元真实数据集上进行聚类。其中CFSFDP算法中需要考虑截断距离选取的问题,算法选择邻近的平均数据点数是总数据点数的1%~2%作为截断距离,本文选取1%~2%中结果最好的作为参数。DBSCAN算法选择使得结果最佳的参数Eps和MinPts作为最终结果。K-means算法预设类别数5,运行10次取平均值作为最终结果。DPC-KNN算法需要选取KNN的百分比参数,按照经验本文选取百分比p为样本数的0.1%,0.5%,1%中聚类效果最好的参数作为最终选择。本文的改进算法参数ρ取聚类结果最佳时的结果。聚类评价指标使用准确率ACC、调整互信息指数AMI以及调整兰德指数ARI,每个指标值在0~1,且值越大表明聚类效果越好。 本文使用的微学习真实数据集经过LSA模型的结构化后,经过SVD分解降维,从原先1 131维高维语义空间映射到k=100的低维语义空间,较好地避免了传统使用VSM模型导致的特征空间高维稀疏性问题。微学习单元真实数据映射到二维空间的几何形状图如图5所示,本文提出的改进的密度峰值算法及CFSFDP算法在微学习单元真实数据上运行得到的几何形状图如图6所示。 从图5中可以看出,微学习单元数据每个类别的全局一致性较强。在图6b中原算法由于使用依赖于截断距离和人工监督的方法,在微学习单元数据中尽管已知真实微学习单元数目,由于不同类微学习单元数据间距离较同一类微学习单元数据间距离更近,且欧氏距离度量使得数据点间全局一致性不足,使得在聚类分配阶段出现误分类,从而导致聚类效果不如用本文算法的。如图6a所示,由于本文算法采用了更适用于微学习单元真实数据的新的密度定义方式,该方式中距离判据为密度敏感距离,使得真实数据集中数据点具有全局一致性,在聚类分配阶段能获得更好的聚类效果。除此之外,改进算法采用了可以自动确定微学习单元簇数的方法,该方法采用残差分析线性拟合决策图中的2个字段找到所有奇异点,并通过约束条件将密度峰值中心选择出来,所以该算法相比原算法拥有更优的性能。 Figure 5 Geometry diagram of micro-learning unit real datasets图5 微学习单元真实数据集几何形状图 Figure 6 Running results of improved algorithm and original algorithm on real datasets图6 改进算法及原算法在真实数据集上的运行结果 表3所示为对比实验的参数设置及各聚类性能指标,其中,CI表示算法中实际的簇数,Par代表每种算法的参数设置情况:改进的密度峰值算法参数为伸缩因子ρ,CFSFDP算法参数为截断距离选取百分比,DBSCAN算法参数Eps和MinPts通过“/”分隔,分别表示邻域距离和邻域内样本数,K-means算法参数为真正的簇数k。 如表3所示,与原算法CFSFDP相比,改进算法可以准确确定簇数,而原算法由于真实数据集数据复杂度较高,在决策图中很难得到正确的簇数和簇中心,所以改进算法在准确率上比原算法高,并且在AMI和ARI上也体现出了改进算法在微学习真实数据集上的优越性,本文可以认为改进算法对于原算法而言有一定的提高。通过与DPC-KNN算法对比,发现使用KNN(K最近邻)作为局部密度的定义方式的算法的准确率、AMI、ARI低于使用密度敏感距离新定义的密度方式的算法的,由于DPC-KNN算法分配策略与本文提出的聚类算法的一致,但DPC-KNN算法选择峰值中心不够智能,为此本文认为,改进算法在微学习单元文本数据集上聚类效果更优。通过与经典的算法对比发现,K-means算法在指定类别数的前提下,其准确率在4个算法中最低,说明了该算法在此处真实数据集上表现较差。从DBSCAN算法通过调整2个参数得到的结果来看,其聚类准确率仅次于改进算法的,但是该算法调参过程复杂,AMI和ARI2项指标均低于改进算法的,可以看出改进算法相比DBSCAN算法有着较大的优势。 如图7折线图所示,本文提出的改进算法在不同的微学习单元类别中的准确率均高于其他对比算法的,通过不同微学习单元准确率的直观表现可以得出这样一个结论:本文提出的改进密度峰值算法在微学习单元真实数据集上更加有效。 Figure 7 Accuracy comparison of different algorithms in each micro-learning unit class图7 不同算法在每个微学习单元类别中的准确率对比 本文提出一种基于LSA模型的改进密度峰值微学习单元文本聚类算法,通过LSA模型和SVD奇异值分解方法缓解VSM模型存在的高维稀疏性,并在原密度峰值算法的基础上引入密度敏感距离,并重新定义密度,避免了原算法类簇分配时的全局一致性不足及截断距离敏感的问题。同时,本文利用线性拟合残差分析找到野值点的方法自动选取密度峰值中心,消除了原CFSFDP算法中人工监督的选取方式对准确率和效率的不利影响。本文在真实的微学习单元数据集上和CFSFDP算法及其他经典的算法进行对比后发现,所提出的算法获得了较好的聚类性能。使用本文算法可以组织微学习资源,从而帮助学习者进行个性化学习。 但是,由于本文算法引入了密度敏感距离,增大了算法的时间复杂度,因此将在今后的工作中对此进行改进。3 新的微学习单元文本聚类算法的研究

3.1 微学习单元模型构建

3.2 基于密度敏感距离的局部密度
3.3 自动选取密度峰值中心

4 实验和结果
4.1 实验相关介绍

4.2 实验实施


4.3 分析真实数据集实验结果



5 结束语

