一种基于凝固地理系的捷联惯导极区导航算法
中国空空导弹研究院,洛阳 471000
地球的两极地区存在丰富的自然资源。出于科学、经济、军事战略等方面的考量,世界大国在两极地区均从事着勘测活动。在南极地区各国建设的机场有50座之多,美国拥有13座,俄罗斯有8座,英、法、德、日等国均有极地机场,我国也正在建设第一座永久性南极机场。这对导航技术提出了更多的要求,需要飞机与舰船具备极区导航能力。
目前,随着中国对两极地区经济以及军事需求的增加,国内对极区导航领域的研究也渐渐活跃。由于中国地理位置远离极地,客观上造成对极区探索的不足,对极区的研究也相对滞后,研发的航空惯导系统也不具备极区飞行的能力。
传统的指北方位平台惯导力学编排在高纬度地区存在方位陀螺施矩困难的问题,捷联惯导则存在计算溢出问题。在高纬度地区纬度圈越来越小,最终收于一点,沿着纬度圈的运动半径也最终变为零:
为了解决这个问题,游动方位惯导系统和自由方位惯导系统被提出。这两种方法可以解决惯性导航系统在极区遇到的上述问题,但由于在地理极点附近,由于真北方向失去定义导致自由方位角和游动方位角失去定义,航向无法给出,即采用这两种机械编排的惯性导航系统能够实现在地理极点附近导航上不出现奇点,但从方向余弦矩阵中提取航向和位置信息时存在奇异值。
为此,又提出了以下几种适用于极区的惯性导航方法:文献 [1-2]提出了格网导航, 这是目前比较成熟的一种极区导航方案,基于圆球模型的力学编排存在原理性误差,而基于椭球模型的力学编排非常复杂、计算量大。文献[3-9]提出了横向经纬度导航, 横向经纬度导航将地球模型当作圆球模型,通过坐标变换将极点转换到赤道上,解决了高纬度地区的导航问题,同样存在着原理性误差。
文献[10]提到了极区平面导航,介绍的极圈力学编排采用了与本文相同的坐标系为导航参考坐标,但是将其简化为了平面导航,存在原理性计算误差。
本文在过去极区导航发展的基础上,以实用、简化算法为出发点,提出一种新的基于凝固地理系的极区导航新方法,该导航模型基于现有椭球模型,无原理性误差,计算量小,是一种传统地理系与凝固地理系的融合极区导航算法,能够满足捷联惯导极区长航时导航需求。
1 凝固地理系下导航算法
凝固地理系(用n表示)定义如图1所示,该坐标系原点位于坐标建立时刻椭球上,轴向与坐标原点处地理系(用t表示)重合,相对于地球固定不动,X、Y、Z对应于北、天、东方向。CGCS2000地球系(用e表示)简称为地球系,机体系用b表示。
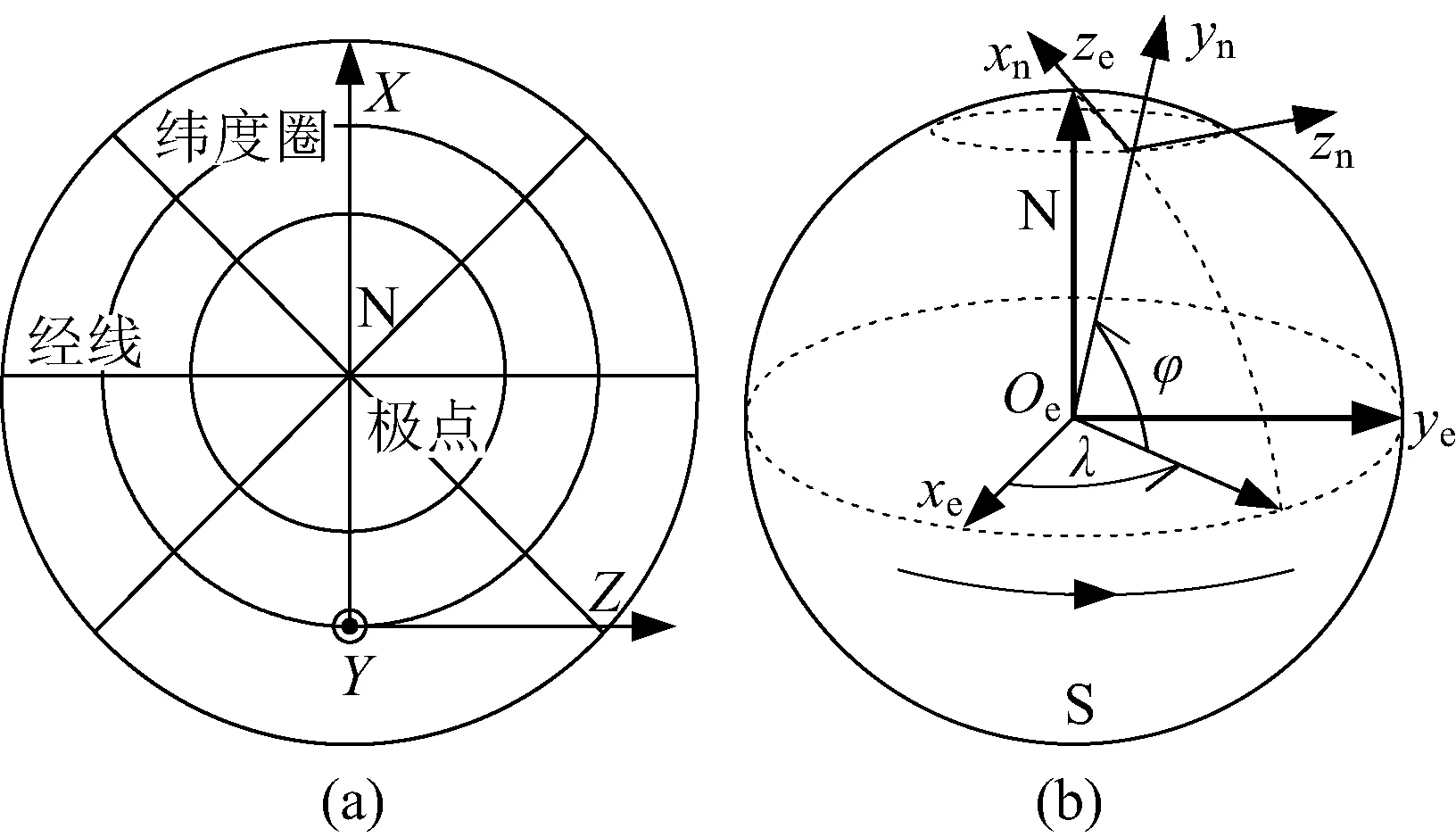
图1 凝固地理系Fig.1 Frozen geography frame
传统指北方位导航力学编排如下:

由于凝固地理系与坐标系建立时刻的地理系重合,地理系下导航参数可以直接作为到凝固地理系导航参数的初值,无需换算;凝固地理系下导航算法相对于指北方位导航算法也更简化。
2 导航参数在不同坐标系下换算
凝固地理系与地理系转换矩阵转换关系如图2所示。
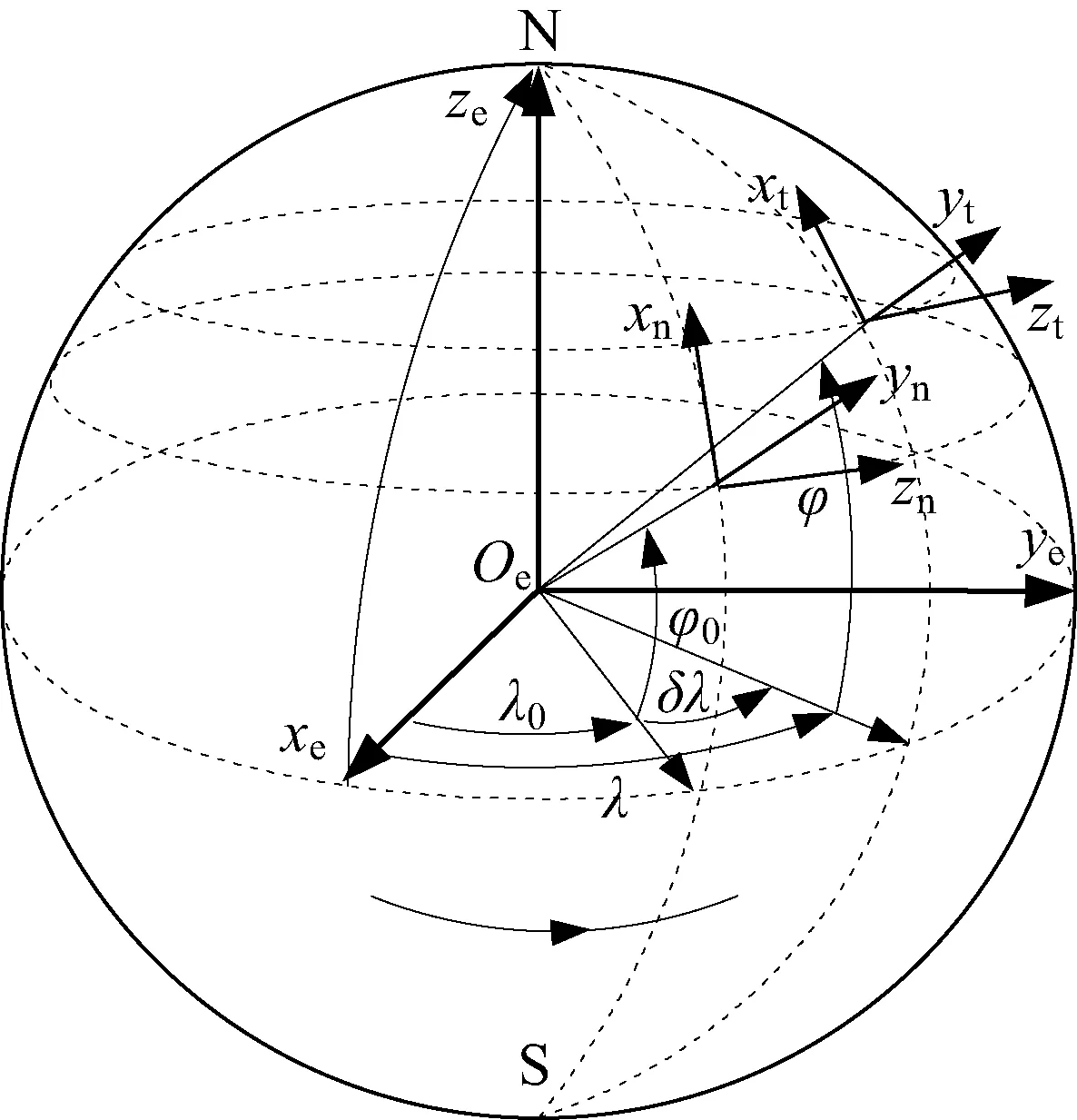
图2 地理系与凝固地理系坐标转换Fig.2 The conversion relation between geography frame and frozen geography frame
凝固地理系导航计算的位置是相对于原点的三轴位置,短距离导航中姿态、速度与地理系导航结果基本一致,可以直接用于描述载体运动状态。
为了便于在不同坐标系下对载体运动进行描述,以下将对凝固地球坐标系导航参数与其他坐标系换算进行说明。
地理系到凝固地理系的换算过程为z轴旋转纬度值φ,绕-x轴旋转经度差δλ,再绕-z轴旋转纬度值φ0。
三次旋转可用旋转矢量表示:
合成四元数为:
Qtn=Q1·Q2·Q3=
用转换矩阵方式可以表示为:
(1)凝固地理系与地球系转换矩阵
换算公式如下:
(2)位置换算
凝固地理系下位置换算到地球系,公式为:
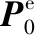
地球系下三维坐标换算到地理系有成熟的算法可用,但是常规算法需要迭代计算,这对于在线实时计算来说是一个计算隐患,会有进入死循环的可能,工程上不推荐使用。
采用如下公式无需循环算法,在实际编程时采用atan2替代atan以实现无奇点计算。
Re=6 368 137 m
Rp=6 356 752.314 2 m
λ=arctan (Y/X)
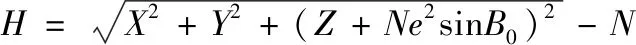
(1)
(3)速度换算
(4)地理系下姿态计算
Q=Qtn·Qnb
提取的航向、俯仰与滚动角公式如下:
θ=arcsin 2(Q1Q2+Q0Q3)
(5)凝固地理系到横轴地球坐标系的换算
对于有横向经纬度导航需求的应用环境,凝固地理系下导航参数可以借助地理系进行换算以获得横轴坐标系下参数,见文献[4],而无需将核心导航算法修改为有原理性误差的横向经纬度力学编排。
本文给出一种凝固地理系到横轴地球坐标系位置的直接转换算法,公式如下:
横向地球系高度直接利用公式(1)进行计算。
速度与姿态计算公式见文献[4],其中地理系下经纬度,使用坐标原点的经纬度。
(6)凝固地理系到格网系导航参数的换算

通过以上换算,可以保持核心算法与软件不变,就可以满足其他导航方式的需求,关键在于不存在原理性误差。
3 软件流程
两种导航坐标系下的导航算法在经过某个纬度圈时进行坐标系与算法的切换,本文采用图3所示流程进行设计。其中a为设定的采用凝固地理系导航坐标系纬度点,b为凝固系坐标导航退出纬度点,并且a>b,这两者设定为一个小偏差,比如为6′。这样的设定是防止边缘飞行时,出现算法频繁切换。

图3 算法与软件设计切换流程Fig.3 Algorithm and software switching process
4 仿真校验
(1)切换点纬度的确定
指北方位导航在接近极点时,由于正切函数原因导致计算溢出,所以当纬度增大到特定值时刻切换为凝固地理系导航,以规避该问题。
正切函数在角度越接近90°过程中数值快速增大直至无穷。经过数值计算可以确定指北方位系统导航方程89.5°附近,并不会出现计算溢出,选择88°~89.5°纬度圈较为恰当。本文确定以89.5°纬度圈为坐标系切换线,即高于该纬度后将指北方位导航切换为凝固地理系导航。
(2)导航仿真
为验证捷联惯导系统导航算法在极区的正确性以及性能,需要进行仿真试验。为避免数值求解在极区遇到的问题,通过解析法给出陀螺和加速度计的输出。
本文采用沿经线向北飞越极点,然后飞出极区的轨迹。仿真参数设置如下:初始纬度89°,经度120°,飞行高度1 000 m,北向飞行速度100 m/s,保持匀速直线平飞,无惯性器件误差,仿真总时间设定为2 000 s。仿真时间558~1 676 s内为进入与飞出89.5°纬度圈的时间,即凝固地理系下导航时间段,约1 117 s为穿越极点时刻,其余时间为指北方位北天东地理系下导航时间。
凝固地理系位置导航参数见图4。

图4 凝固地理系下位置Fig.4 The position under frozen geography frame
图中可见凝固地理系导航系下保持了无东向运动,由于地球曲率影响,凝固地理系下高度一直在下降。进入与飞出89.5°纬度圈,X轴的运动距离约为110 km。
凝固地理系姿态变化见图5。

图5 凝固地理系下姿态Fig.5 The attitude under frozen geography frame
图中可见凝固地理系下载体俯仰角一直负向变化,航向与横滚角一直保持不变。
为了形成完整不间断的地理系参数,需要将凝固地理系下参数转换至地理系,以形成完整的指北方位参数,地理系下位置信息如图6所示。
图6中可见飞过极点时经度从120°立即跳变为-60°;飞行高度维持在1 000 m。
地理系下姿态如图7所示,图中可见航向角飞过极点后,立刻从北向0°切换为南向-180°方向。
下面将对导航误差进行计算,将全段经纬高参数转换至地球系下与轨迹进行对比,姿态信息在地理系对比以分析算法误差特性。
地球系下位置误差如图8所示。

图6 地理系下位置Fig.6 The position under geography frame

图7 地理系下姿态Fig.7 The attitude under geography frame
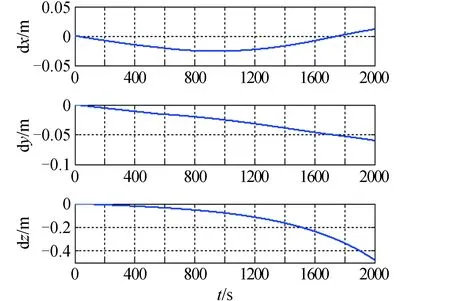
图8 地球系下位置误差Fig.8 The position error under the earth frame
从图8中可见导航坐标系切换过程并不影响惯导误差发散的趋势与大小,位置误差变化保持连续,无跳点。
地理系下姿态误差如图9所示。
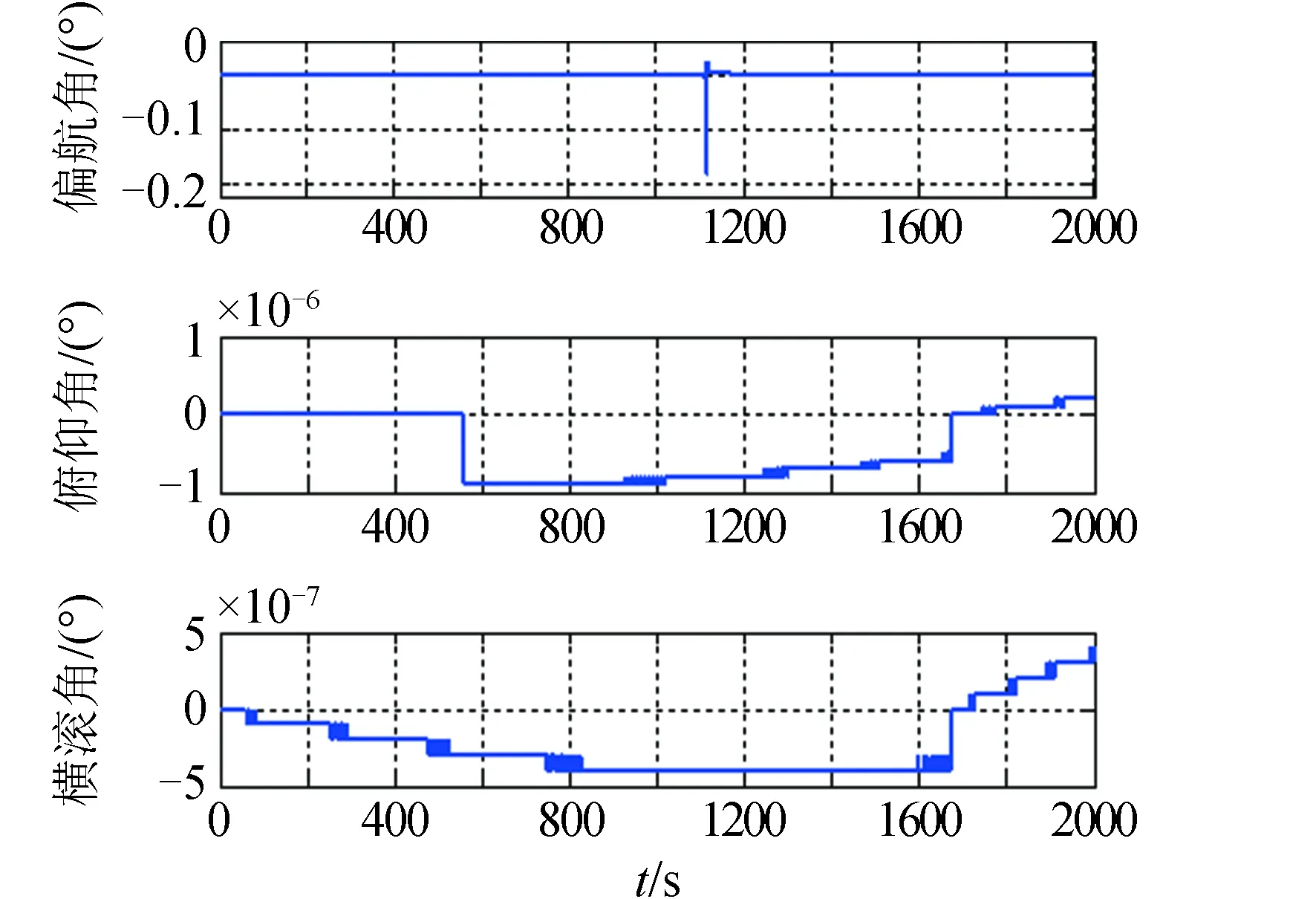
图9 地理系下姿态误差Fig.9 The attitude error under geography frame
5 结束语
凝固地理系导航是在指北导航力学编排基础上,删除会导致计算溢出项。依旧按照地球的椭球模型进行导航,不存在原理性误差。
原理上凝固地理系属于地球系的一种,是将原点从地心挪到了椭球面,其力学编排适合全球导航,但是过长距离导航将使得凝固地理系下导航参数失去直观的物理意义,最终要将参数转换到地理系下才能表征载体的运动状态。将该坐标系用于距离原点200~300 km内的导航是必要的。本文以89.5°纬度圈为界限,直径约为110 km;在载体位置低于该纬度圈后切换回原来导航坐标方案,这是一种恰当的极区导航解决方案。仿真和分析结果表明:本方案导航算法简单,计算量小,导航精度高,无原理性误差。
本文与其他极区导航方法的不同,在于不追求形式上的全球统一方法,该坐标系的使用限于极区小范围,超出范围仍旧切换回通用的地理系。

