一种地月转移轨道中途修正的制导算法

上海微小卫星工程中心，上海 201203

探测器在地月转移过程中，由于各种误差的存在，实际轨道偏离标称轨道。为确保探测器顺利进入目标轨道，探测器在飞行期间需要进行多次修正。中途修正解决的问题有两方面：如何确定修正时机使修正速度总量最少;终端误差满足任务要求及如何确定单次修正速度增量。

针对第一个方面的研究相对成熟[1-5]，这里只做简单的介绍。国外研究中有间距比策略[1]，即尽快进行第一次中途修正，以后各次修正时机的选择是按照修正效果与前一次修正效果的比值为常数这一条件确定的。国内研究主要围绕嫦娥探测器展开，文献[2-3]给出了典型的两次中途修正策略，即第一次修正在飞行的第一天实施,第二次修正在到达月球的前一天实施。

本文主要针对第二个问题展开研究。其本质上是一个两点边值问题，由于三体动力学的复杂性，不存在解析解，必须利用数值方法进行求解。一般的思路是：首先根据边值约束，采用简化模型设计初值，之后考虑精确摄动模型，采用微分修正等数值方法求解。

对于地月转移轨道中途修正问题，可以将实际速度作为初值，若探测器实际速度误差过大，初值精度变差，修正算法的求解性能降低，因此有必要对初值进行改进。若修正时刻探测器的位置在月球段，探测器主要受月球引力的作用，初值设计本质上是求解二体Lambert问题，文献[6-8]给出了经典的求解方法，若在地球段，需要考虑月球引力的影响，目前设计方法有圆锥拼接方法[9-15]，但圆锥曲线拼接方法精度有限，导致修正算法的求解效率降低。

在使用微分修正求解精确解时，需要计算状态转移矩阵，在常用的数值方法中[3,16-18]，首先需要推导加速度相对位置速度的偏导数矩阵，然后同时积分动力学方程就可以得到状态转移矩阵，但在每次迭代计算中，需要积分42个方程，导致求解时间增加。

针对以上研究现状，本文首先利用伪状态理论，结合Vinti预报方法[19]，设计高精度的初值，在求解精确解时，提出了一种基于伪状态理论的状态转移矩阵解析算法。该算法通过设计高精度的初值，降低了求解修正速度增量的难度，而且避免了传统数值方法计算状态转移矩阵的复杂性。

1 问题描述

由于修正时刻探测器的位置无法改变，只能将速度和转移时间作为设计变量，本文采用转移时间固定的修正策略，因此初始修正参数只有速度3个分量，即：

(1)

式中：v01，v02和v03分别为修正时刻探测器在地球惯性系下的速度分量。

对于月球探测任务，通常对到达月球时刻的月心距、轨道倾角以及飞行角有严格要求，因此选取目标轨道参数为：

(2)

式中：rp，iL以及γL分别为到达月球时刻探测器的月心距、月球固联系下的轨道倾角以及相对月球的飞行角。

2 伪状态理论

伪状态理论是文献[20]提出的一种地月中心引力作用下的轨道近似计算方法。

令tI时刻探测器相对地球的状态为ΣI=(RI,VI)，利用伪状态理论计算tk时刻探测器相对地球的状态Σk=(Rk,Vk)和相对月球的状态σk=(rk,vk)。定义以tk时刻月球位置为中心的伪状态转换球(Pseudostate Transformation Sphere,PTS)，半径为RPTS，在本文算例中，其值取为24个地球半径。假设RI在PTS外部，Rk在PTS内部，如图1所示。

图1 伪状态理论Fig.1 The pseudostate theory

具体计算步骤如下：

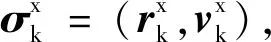
(3)

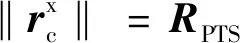
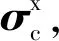
3 初值设计

3.1 初值求解

本节给出了地球惯性系下的中途修正初值的求解方法。令修正时刻探测器位置R0，到达月球时刻tL，转移时间Δt，迭代变量RS，求解过程如下：

1)计算tL时刻月球相对地球的位置速度分别为RM和VM，令RS=RM。

2)利用Lambert算法，求解R0到RS，转移时间Δt的地球二体轨道，可得到R0和RS处的速度V0和VS。

3)计算tL时刻探测器相对月球速度在月球固联系下的经度aL和纬度δL，求解tL时刻探测器在月球固联系下的升交点经度ΩL,

sin(aL-ΩL)=tanδL/taniL

(4)

根据式(4)，ΩL有两个解，对应到达月球的升降轨方式，则角动量hL在月球固联系下的表达式为:

hL=[siniLcosΩL-siniLsinΩLcosiL]T

(5)

4)令探测器在PTS边界时相对月球的位置和速度分别为rS和vS，对于地月转移轨道，rS在近月点前，大小为RPTS，根据能量守恒，可得近月点速度大小为：

(6)

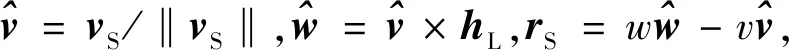
(7)

令rS到近月点的转移时间为tS，根据伪状态理论可得

(8)

3.2 地球扁率影响的修正

对于地月转移轨道，地球扁率摄动是一项不可忽视的摄动源，因此在精确初值设计时，需要考虑地球扁率的影响。

在求解地球扁率摄动的解析方法中，Vinti预报方法精度高，速度快，因此采用Vinti预报方法来修正地球扁率摄动的影响，求解过程如下：

1)求解R0到RS，转移时间为Δt的地球二体轨道，可以得到R0地球速度V0k。

2)以R0和V0k为初值，利用Vinti预报方法计算tL时刻的位置RSk。

3)更新V0k，其中Jk可近似为二体状态转移矩阵：

(9)

4)若‖RS-Rsk‖大于给定阈值，返回步骤2)，否则，输出V0k作为初值。

4 精确解求解

为得到精确解，必须在更复杂的摄动环境下通过数值积分计算精确的转移轨道，然后采用微分修正方法对初值进行修正。在精确的转移轨道计算中，本文考虑了地球非球形项，日月中心引力的影响，其中，地球非球形引力取8×8阶，月球和太阳星历均采用DE405。

初始修正参数P和目标轨道参数Q存在确定关系，记为Q=g(P)，则存在以下关系:

(10)

根据微分修正方法，在每次迭代中初始修正参数的调整量为:

(11)

式中：ΔQ为目标轨道参数的偏差量。令状态变量X=[R,V]T，R和V分别表示探测器在地球惯性下的位置和速度，则式(10)可以重写为：

(12)

式中：Xi，Xf分别为状态变量X的初始状态和终止状态。式(12)误差传递矩阵计算中，除状态转移矩阵Φfi外均有确定的形式。三体轨道动力学特性导致Φfi没有解析表达式，通常采用数值方法计算。为提高求解精确解的效率，本节给出了一种基于伪状态理论的状态转移矩阵近似解析计算方法。

根据伪状态理论，存在以下关系:

(13)

式(13)第一项具体表达式为:

(14)

(15)

式(13)第二项可以分解为以下两项：

(16)

(17)

式中：

(18)

根据关系式：

(19)

对式(19)求导可得：

(20)

5 算例与分析

本节给出了一个地月转移轨道中途修正的求解算例，首先根据本文给出的初值设计方法给出初值，然后利用解析状态转移矩阵求解精确解。

假设探测器在2022年1月1日进行修正，此时探测器在地球惯性坐标系下位置为[-4 094.687，4 730.547，2 588.812] km，转移时间为72 h，近月点高度为600 km，达到月球时轨道倾角25°，到达月球方式为升。

在无奇异情况下，Lambert问题具有长短程两个解，所以目标轨道参数确定以后，中途修正有两个解，相应的轨迹如图2所示，其对应的地心张角不同。经过计算可以得到两个可行解。其中：短程解为v1=[-8.564 25，-5.888 53，-2.785 82] km/s，长程解为v2=[9.184 99，5.093 68，2.351 90] km/s，v1和v2夹角为174.2°，方向几乎相反。

图2 地月转移轨道Fig.2 Trans-lunar trajectory

通常长程解被忽略，但在某些任务中，如探测器并非直接由运载送入地月转移轨道，而是在近地轨道上依靠自身推进系统进入地月转移轨道，长程解可作为地月转移轨道的选择，本文算法直接可以设计地月转移轨道。

下面通过一个算例来说明本文算法的求解性能。选择一条标准地月转移轨道，其发射时刻为2022年1月1日，转移时间120 h。近地点高度为300 km，地球出发时轨道倾角为25°，地球出发方式为降轨，近月点高度为500 km，到达月球时轨道倾角为35°，到达月球方式为升轨，在地球惯性系下，探测器出发时刻的标称位置速度分别为[ -5 848.290，2 683.276，1 760.631] km和[-5.135 05，-8.845 35，-3.576 42] km/s。假设探测器进入地月转移轨道时半长轴偏差为10 000 km，在入轨24 h后进行修正。

如果将实际速度作为修正初值，其搜索过程如表1所示，由于误差过大，导致迭代发散，无法得到精确解。若采用精确的初值，经过8次迭代就可得到精确解，迭代过程如表2所示。通过初值设计，提高了初值精度，保证了修正算法的收敛性和效率。

表1 近月点状态偏差迭代过程Table 1 Iteration of the error of perilune

表2 利用精确初值的近月点状态偏差迭代过程Table 2 Iteration of the error of perilune using the initial solution with high accuracy

表3给出了相同计算条件下(Intel Core 2.53G),分别利用解析法计算状态转移矩阵(简称解析法)和数值法计算状态转移矩阵(简称数值法)求解精确解的计算结果，尽管两种方法均可以得到精确解，但若采用解析法求解状态转移矩阵，计算时间更少，求解效率更高，而且算法结构简单，避免数值计算的复杂性。

表3 计算结果Table 3 Simulation results

6 结束语

本文针对地月转移轨道中途修正问题，提出了一种求解修正速度增量的方法。该算法通过改善初值的精度和简化状态转移矩阵，提高了地月转移中途修正的求解效率，可有效解决地月转移中途修正问题，可为月地转移等深空探测轨道设计以及中途修正提供借鉴和参考。