核心素养:从顶层设计到课堂落地


摘 要:“核心素养”的顶层设计,是基础教育课程改革的创新点和突破点。核心素养如何在数学课堂落地?当学生习得数学学科六大素养之后,应该带走哪些关键能力?当学生忘却所有的数学概念,公式和原理之后,应该留下哪些数学品格?我们在教学实践中的有效应答是数学的眼光,数学的思维和数学的思想。
关键词:核心素养;数学眼光;数学思维;数学思想
“核心素养”的顶层设计,是基础教育课程改革的创新点和突破点。如何让核心素养从顶层设计到课堂落地,每一位教师必须用个性化教学实践进行有效应答。本文以小学低年级数学《比大小》教学为例,探讨在课堂教学活动中融入学科核心素养培育,让学科核心素养在课堂落地生根。
一、 让孩子用数学的眼光提出问题
荷兰教育家汉斯、弗赖登塔认为:“数学来源于生活,存在于现实、并且应用于现实,教学过程应该是帮助学生把现实问题转化为数学问题的过程。”
问题生于情景,情景源于生活。教材中的数学知识从生活中提炼,以情景的方式呈现,每一个孩子都用自己的眼光来解读,角度不同,问题就各不相同。“知识为本”的教学不重视学生的生活经验,太过于注重知识的传授,忽略“还原”知识的发生与发展及个体的体验和感悟,缺乏对学生创新思维和核心素养的培育。为此,核心素养视野下的教学要从唤醒学生的生活经验出发,创设有利于学生问题意识的教学情景,持续不断培养学生从数学的角度用数学的眼光来观察数学的发生与发展,亲历知识的成长与演化,促进素养的积累与沉淀。
案例:一年级上册第三单元“1~5的认识和加减法”中的“比大小”教学。
图1
【片段教学1】
师:仔细观察(图1)你会找到那些数学信息?你能提出数学问题吗?
生1:猴子有3只,猴子最爱吃桃子?
生2:我觉得香蕉好吃?
生3:梨有几个?
……
师:小猴们到森林里游玩……共进午餐的时候,他们想一起分享自己带来的水果。看,草地上的水果真多啊!大家来数数,小猴和水果分别有多少?
生:略。
师:每只小猴子吃1个梨、1個桃、1根香蕉,这些水果够分吗?
学生对情景图“小猴吃水果”观察的最初问题是比较杂乱的“猴子最爱吃桃子?我觉得香蕉好吃?梨有几个?……”这些现实问题的萌发,是学生基于自己生活经验,而不是数学学科的角度,即使有些是数学问题,也未必是学生有意识主动从数学的角度思考的,绝大部分的学生对情景图的观察都只是观赏性地停留在表面。为此,教师拓展丰富情景,创设童话故事,引导学生聚焦数学核心问题“每只小猴子吃1个梨、1个桃、1根香蕉,这些水果够分吗?”。教师的提问促使学生必须从生活中现实的经验问题转向为数学角度的问题进行思考:“猴子有几只?水果是多,还是少?要把散乱的水果分一分?……”此时,学生就要用数学的眼光去观察情景,会有意识地把“猴子吃水果”与“数”建立起联系,学生一旦用数学的眼光看情景就非常有利于学生数感的形成,反之数感的建立有助于学生用数学的眼光去发现问题。因此,情景化和问题化在以核心素养为本的教学中具有重要价值,学生可以在情景与问题的联系中,重构枯燥的知识和真实的现实,从而逐步学会用数学的眼光看世界。
二、 让孩子用数学的思维分析问题
数学思维是数学核心素养的重要组成部分,其中思维的问题性、概括性、逻辑性是学生思维能力的重要表现。学生的数学思维水平直接影响其分析问题解决问题的能力。而“问题”作为数学课堂教与学互动的重要载体,它不仅推动着数学知识的成长与演化,也推动着学生思维的运作和发展。教师要用数学核心问题引导学生分析问题,发展思维,主动建构“自己的数学”。
【片段教学2】
师:把水果分一分,看看哪一种水果多?哪一种水果少?
生:把相同的水果放在一起,就是桃子跟桃子,香蕉跟香蕉,梨跟梨。
师:小朋友已经把同类的水果放在一起。怎样摆水果,能够一眼看出哪一种水果多,哪一种水果谁少呢?用学具摆一摆。
生:我把水果一个一个地对整齐,发现梨比较多,香蕉比较少。
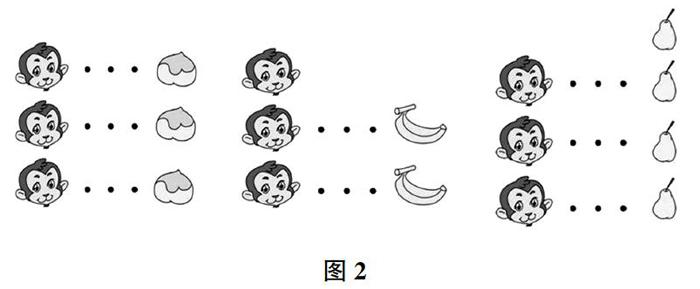
课件展示:情景中的猴子和水果点击跳动下来,摆成象形图(图2)。
图2
师:刚才,我们用了“一一对应”的方法摆出了象形图。请你观察象形图,数一数有几只猴子吃几个桃子、香蕉和梨?
生回答后,教师板书:“3、4、3、2”。
师:有1只小猴,就有1个桃子,有3只小猴也有3个桃子,猴子的只数与桃子的个数有什么关系?
生:一样多(相同、相等、同样多)。
师:每只猴子吃一个桃子,不多不少,猴子与桃子的关系,你用一句话说一说吧。
生1:小猴和桃子同样多。
生2:3只猴子与3个桃子同样多。
师:对,同样多,可以用“=”表示,“3=3”。
对于核心问题“每只小猴子吃1个梨、1个桃、1根香蕉,这些水果够分吗?”的分析思考,教师通过系列问题来引领学生分类,一一对应竖直排成一列,统计数量,再比较大小,推动数学知识“同样多”的发生。在操作—观察—概括—表达的过程中,学生从情景和直观图中抽象出数字“3、4、3、2”,学会用数学表达“同样多”,理解“=”含义,更重要的是学生的动作思维,形象思维,逻辑思维都得到了发展。在随后学习“3>2”“3<4”时,教师可以启发学生根据给出的问题按照“观察—概括—表达”的逻辑步骤主动分析解决问题。
【片段教学3】
师:观察象形图,猴子和香蕉的数量谁多,谁少?你是怎么知道的?
师:同桌互相说一说猴子与香蕉的关系。
师:你能创造一个符号来表示吗?
三、 让孩子用数学的思想解决问题
数学思想是数学学科核心素养的核心,它不像“双基”通过短期的集中训练便能掌握,数学思想需要在长期的教学中渗透和影响才能形成学生潜意识地在现实生活中用数学思想面对真实世界的品质特点。古语云“泰山不让土壤,故能成其大;河海不择细流,故能就其深”。教师要在每一节课的教学或每一次的活动中,适时、适当地落实数学思想与方法,使学生在潜移默化中日积月累,才能让数学思想在不断地内化中塑造着学生的精神个性品质。
【片段教学4】
师:猴子和香蕉的数量谁多,谁少?你是怎么知道的?
生1:我用数数比较,发现猴子有3只,香蕉只有2根,猴子比香蕉多,所以不够分,不够吃。
生2:我从象形图中看出来,猴子排列的比香蕉高,所以猴子多,香蕉少。
师:猴子与香蕉比较怎么说?同桌互相说一说。
生:猴子比香蕉多。
師:猴子比香蕉多,你能不能创造一个符号来表示猴子与香蕉之间的关系呢?(图3)
生1:用语言文字表示(3多,2少)。(板书)
生2:我用记号表示多,谁多就记它旁边(3* 2)。(板书)
生3:谁多就用对号,谁少就用错号(3√ 2×)。(板书)
生4:我知道用大于号(3>2)。(板书)
图3
师:猴子比香蕉多,小朋友用自己喜欢的方式表示出来,真棒!大家再来看看,谁的符号最好?说说你的理由。
对于数学新的知识“>”的发生,教师在这里没有用讲授的方法直接告诉学生。学生是在具体的情景中去抽象“比多”和“比少”,再创造符号来“数学地”表达,在此过程中学生感受了统计思想、一一对应思想、抽象思想和符号化思想。这样,在从数学核心问题的追寻开始,就渗透着数学思想与方法,才有可能在必备品格烙上数学思想的印记。
总之,核心素养视野下的教学,需要教师在顶层设计的理念指导下,进行教学的创造实践,通过变革教学方式和学习方式,最终实现核心素养培育的“授之以渔”。唯有如此,这才是我们所期望的课堂愿景。
参考文献:
[1]王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014.7.
[2]马云鹏.小学数学核心素养的内涵与价值[J].小学数学教育,2015(5).
[3]王岚.从理解到行动[N].中国教师报,2017-3-29.
作者简介:
陈善建,福建省福州市,福建省福州市吴庄华侨小学。

