数形结合在函数问题中的应用

黄定红

摘要：本文对数学结合在函数问题中的应用，从函数图形转函数，函数转图形，函数和图形之间互相转换的三个方面提出了探讨，为数形结合解决函数问题的策略提供参考。

关键词：数形结合;函数;数学

函数图像是函数概念在二维环境下的直观展现，是解决函数问题的突破口。函数图像能够清晰的展现出函数的性质和规律，了解函数与变量之间的关系，有助于函数问题的解决。在进行函数学习的时候，要善于利用函数图像辅助函数解题，利用数形结合的思想能够有效提升函数学习的效果，增强数学学习能力。

1.数形结合中的以形助数思想在函数问题中的应用

通过函数图形帮助函数问题的解决，是初中阶段用来解决函数学习的最主要的方式之一。借助图像所具有的生动、直观的特点，把数量之间的变化关系表现的非常直观形象，一眼就能发现其中的规律，这也让解题思路变得更加清晰起来。

因为数字本身所具备的抽象、零碎的特性，如果在解决函数问题的时候，纠结于数值上面，就会加大函数解题的难度，增加了干扰项。所以要从“数”的领域转变成“形”的领域，利用图形去解决问题。

核心思路是把以数为主的问题转换成以形问题，先去解决函数图形当中存在的问题，最后再次解决函数的问题。

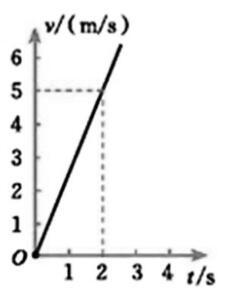
例如在学习一次函数的过程中，给出题目：“一块冰块沿着管道向下滑，它的速度v（m/s）与冰块下落时间t（s）的关系如图所示。

（1）试写v与t之间的关系表达式;

（2）当冰块滑落3s时冰块的速度是多少？

教師进行函数教学的时候，通过函数图像将函数中数量间的关系，转变成更加直观、更加形象的直角坐标系，学生可以从图像中观察到数量之间的变化关系（因为图像是一条经过原点的直线，因此该图像为正比例图像）和题意分析可知，变量v与变量t之间呈正比例关系[1]。设v=kt，通过这种方式可以有效的结合已知量和变量，让学生重新通过另一种方式认识到一次函数和变量之间的关系。通过学生自己的观察和分析，寻找出正确的答案。最后根据图像可以看出，当冰块下滑速度在3s的时候，速度达到3k，已知k=v/t且k是定量，所以根据t在2s时v=5可知，k=2.5，所以当t=3时，v=7.5。因此，确定直角坐标系思想模型，可以让学生在对函数问题形象化的分析实践中，达到对问题的有效分析，合理判断，并最终作出对函数问题的有效解答。

通过函数图形去帮助解决函数问题，这之中图形是关键的。在解题的过程中，需要制作正确的图，学会正确用图，最后用正确的逻辑去分析函数图形，是以形助数的基本。要学会从函数转到图形，再从图形转回函数。心理学领域元认知的概念就是认为人只要通过培训，就可以对认识行为进行再认识。因此要在函数的学习中，

做到见“数”如见“图”，将函数的解题思路放在更高一个层次上，才能做到数学学习质量的提升。

2.数形结合中的以数代形思想在函数问题中的应用

在数学函数学习的过程中，经常会出现运用文字的形式表示数与数之间的关系，这不利于数学学习中抽象思维的发展。因此要在数学学习实践的过程中，将函数代数的问题转变成几何图像，用生动形象的几何图形直观的表现函数关系，更有助于引导数学学习，提升对函数问题的认知。

例如在学习反比例函数的过程中，分析例题：若点（-3，y1）、（-2，y2），（0，y3）在反比例图像y=-3/x上，求y1，y2，y3之间的大小关系。根据反比例函数的关系式可以得到直角坐标函数图像，然后再在图像上标注y1，y2，y3三个点所在的位置，对比三个点的大小关系，得出答案。通过以数化形的方式，可以让数量关系在直观图里通过更直接的方式展现出来，不需要通过繁杂的计算就可以轻松对比出大小关系，为函数当中在函数图像的应用扩宽了思考方向。

3.数形结合中的互相变换思想在函数问题中的应用

如果在函数学习的过程中直接给出函数的关系式和图像，那么一定可以很轻松的发现其中的规律，并找到解决的办法。但是如何判断函数的数量具体关系，以及根据这个关系列出正确的关系式，再进行正式的画图分析，则需要更多的考量。数形互换的方法可以很好的解决在单一思路受到阻碍的情况[2]。如果无法确定函数的关系式，那么可以先构画函数图像，通过分析函数图像的增减性，然后判断函数之间的关系，最后再写出关系式。数形互换思想是利用数形结合解决函数问题当中最复杂也是最灵活的方式，如果能做到正确合理的运用，将会对函数思维模型的构建起的极大的推动作用。

例如已知函数y=kx+b（k≠0）和函数的图像相交于点A（m，4）和点B（2，n）两点，并与坐标轴交于M，N两点，求（1）一次函数的解析式，（2）请直接写出kx+b-≥0重的x的取值范围。

解题时要注意发挥数和形的优势，结合数形关系进行分析。根据第一问，根据函数之间的关系计算得出k=-2，b=6，m=1，n=2，所以函数y=-2x+6。如果没有图形作为辅助，那么这道题需要解出kx+b-≥0中的x的取值范围，也就是-2x+6-≥0的范围，难度较大。

我们可以观察一次函数和反比例函数之间的关系和交点，可以看出当反比例函数在第一象限时，仅在m到n点的取值小于一次函数，其他阶段都满足kx+b-≥0，所以根据题目我们可以直接得出当x≤0或1≤x≤2的时候，满足kx+b-≥0。

结论

数形结合思想的研究是对函数解题思路的一种改进，是对认知方法的再认知，有利于提升思想高度去解决函数问题，简化问题的同时寻找到更多的办法，开拓眼界。在数学函数学习过程中，要熟练的掌握好从图形转函数、从函数转图形，再到函数图形互相转换的办法，寻找到不同的解题思路，促进数学思维发展。

参考文献：

[1]王伟平，张宏政.妙用两点构图像立足关联谋整体——函数复习课教学实录及点评[J].中学数学教学参考，2019（35）：33-36.

[2]罗晓彤.数形结合对应为径——数形结合思想方法在函数综合问题中的应用分析[J].中学数学教学参考，2019（35）：66-69.