基于二进制电抗分流器实现热电变换器共地测量

潘仙林， 张江涛， 石照民， 宋 莹， 贾正森， 王嵘瑜， 丁 香

(1. 中国计量科学研究院，北京 100029； 2. 贵州省计量测试院，贵州 贵阳 550003；3. 北京市计量检测科学研究院，北京 100029)

1 引 言

热电变换器(thermal voltage converter,TVC)是目前将交流电流/电压转换为等效直流电流/电压量的最准确的标准器[1～3]。普遍采用薄膜结构平面多元热电转换器[4，5]，并结合精密分流器，基于step-up爬台阶法建立各国交流电流国家基准[6，7]。

热电变换器往往通过并联的连接方式，与高精密同轴分流器构成不同电流量程标准，采用串联连接方式进行交直流转换测量实现交流电流量程扩展。热电变换器和分流器组合在串联模式下，影响转换误差的一项主要因素是来自于热电变换器输入端与输出热电势端之间的容性泄露电流影响，这种影响在较高频率时更为明显[8]；另一项影响因素来自于串联模式下电流三通所引起的泄露影响[9]。瑞典国家计量院Rydler提出了一种高精度交直流电流转换自动测量系统，使得热电变换器工作在对称状态从而减少泄露电流的影响[10]。

中国计量科学研究院采用二进制电抗分流器(binary inductive current divider,BICD)的方法建立了热电变换器和分流器组合之间共地比较测量装置。该装置通过二进制电抗分流器实现两路共地电流输出，将被比较的热电变换器和分流器组合分别连接在2支路电流中，实现共地测量，从而消除串联模式下泄露电流所引起的测量误差。

2 串联连接测量模式

各国普遍采用热电变换器结合分流器作为交流电流量程扩展的标准器，采用不同电流量程的分流器和热电转换器进行组合，并通过step-up爬台阶法将被比较的两套热电转换器和分流器的组合进行相互串联，基于交直流转换方法实现两者之间相互比较，从而实现交流电流量程扩展。热电流转换器在串联连接测量模式下，受容性泄露电流和三通连接器导纳等影响，将引起较明显的测量误差。

2.1 串联连接容性泄露

2套热电转换器和分流器的组合采用串联连接方式，图1中所示的简单等效电路模型是评估热电转换器寄生导纳所引起的泄漏电流误差。热电转换器的寄生导纳分别连接在高端和低端的热电偶和加热丝电阻之间，由2个具有相等值的集总泄漏导纳表示。图中，标记为YS2和YT2的热电偶和输入低端之间的漏电导纳要么被短路，要么与电流输入端子并联连接而忽略不计。那么当高端点位的热电转换器输出接地时，热电偶和输入高端之间的泄漏导纳(标记为YS1和YT1)将分别引起漏电流IS1和IT1。在串联模式下，被比较热电转换器交直流差受容性泄露电流所引起测量误差δleak可表示为：

δleak=RHS×(YS1+YT1)

(1)

式中：RHS为标准热电变换器自身阻值。

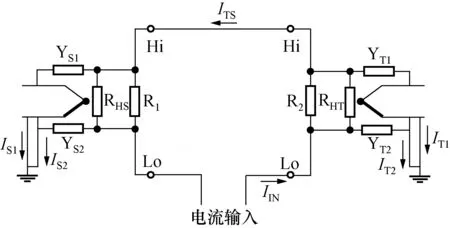
图1 串联模式下容性泄露影响Fig.1 Capacitive leakage influence at in-series connection mode

2.2 串联时电流三通影响

在串联比较模式下，通常采用电流三通来串联两套热电变换器和分流器的组合，如图2所示。由图2可知，三通连接器中各个端子间寄生导纳将导致产生泄露电流，从而引起交直流差的测量误差，尤其是在高阻值和高频率下越为明显。电流三通输入端的高端和低端之间的导纳与电流源的输入端相连，其影响可以忽略不计。当流经三通连接器端子所产生的泄露电流IC1和IC2相等时，才能保证流经R1-TVC1和R2-TVC2的电流一致。那么受电流三通连接器导纳和寄生电容影响，所引起测量的交直流差测量误差δtee可以表示为：

δtee=RT2G2-RS1G1+ω2[RT2C2]2

(2)

式中：RT2和RS1是R2-TVC2和R1-TVC1的等效阻抗;C1和C2是等效电容;G1和G2是T型三通连接器的电导。如果RT2=RS1，即两套热电转换器和分流器组合的等效阻抗相同时，那么三通连接器所引起的测量误差主要来自于连接器自身导纳不一致。

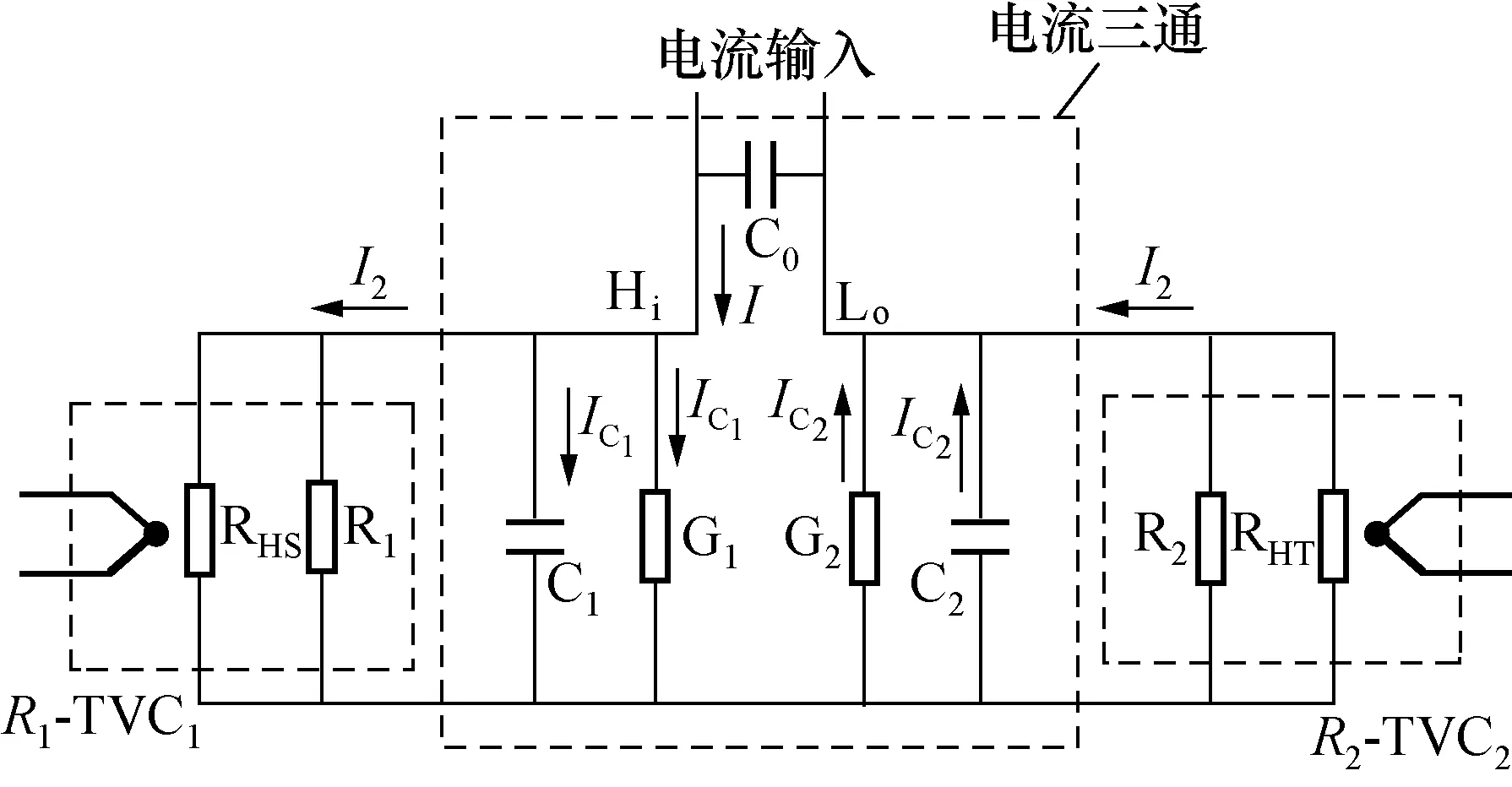
图2 串联连接模式下电流三通结构示意图Fig.2 Leakage influence from current tee connector at in-series connection mode

3 二进制电抗分流器

二进制电抗分流器主要将输入电流均匀等分为2路输出电流，2路电流低端共地且比例关系可自校[11]。二进制电抗分流器的内部结构如图3所示。将双股绞合线均匀绕制在高磁导率磁芯上，将绕组的同名端和非同名端进行首尾相连，连接点作为电流输入端，两路电流将分别接至被比较的热电变换器和分流器组合，电流输入端的低端和被测两路电流低端相连。为了消除磁芯绕组和铜外壳之间的容性泄漏影响[12]，往往采用铜屏蔽结构设计并连接到电流输入高端。Z1S和Z2S是绕组的阻抗，包括导线电阻和漏电感。

图3 二进制电抗分流器Fig.3 Inner structure of the binary inductive current divider

二进制电抗分流器两路电流比例关系的校验方法在文献[13]中已经详细介绍，为了研究两路输出电流在不同负载下的影响，文中选用了1 Ω，10 Ω和90 Ω 3种不同阻值的分流器进行实验分析，测量结果见表1所示。

表1 两路电流在不同负载下比例误差自校验结果Tab.1 The results of self-calibration at different shunts μA·A-1

由表1可以看出：二进制电抗分流器两路电流之间的相对误差在100 kHz的频率范围内优于 5 μA/A 的范围，在200 kHz的频率下优于20 μA/A，同时在不同负载下电流比例变化优于2 μA/A。

4 测量系统

为了减少串联连接方式下容性泄露和三通连接器导纳影响，文中提出了基于二进制电抗分流器实现热电转换器之间进行共地比较测量的方法，测量原理如图4所示。

图4 基于BICD热电变换器比较测量装置Fig.4 Measurement setup for comparing based on the BICD

该装置采用2台交流电压源通过切换开关作为两路交流电压信号输出，驱动跨导放大器实现交流电流输出。将交流电流输出接入二进制电抗分流器的输入端，产生2个电流支路，标记为I1和I2；被比较的分流器RX和RS分别连接在I1和I2支路中，热电变换器TVCX和TVCS分别检测分流器RX和RS上的电压降；通过纳伏表测量TVCX和TVCS的输出热电势，实现2套热电变换器和分流器组合之间在不同频率下的相互比较。

为了减少热电变换器自身输出热电势随时间偏移的影响，在1个比较测量周期中，采用f1，f0，f0，f1测量顺序将交流电流依次流经分流器。2种并联分流器和TVC组合在不同测量频率下频率特性可表示为：

(3)

式中：δSac-ac是RS-TVCS组合在不同频率下相对于f0的相对误差；δXac-ac是RX-TVCS组合在不同频率下相对于f0的相对误差;eXf0和eSf0分别是TVCX和TVCS在频率f0处的输出热电势平均值，eXf0和eSf0分别是TVCX和TVCS在频率f1处输出热电势平均值。理论上TVC输出热电势与分流器两端的输出电压成平方性比例关系，nX和nS分别表示热电变换器TVCX和TVCS的平方性系数。

5 实验结果

热电变换器和分流器组合在串联连接模式下受容性泄露电流和电流三通导纳等因素影响，通过换臂法测量和实验分析，在10 mA,100 mA和1 A电流下对串联所引起的泄露影响进行了测量，测量结果相对于1 kHz交流转换误差见图5所示。

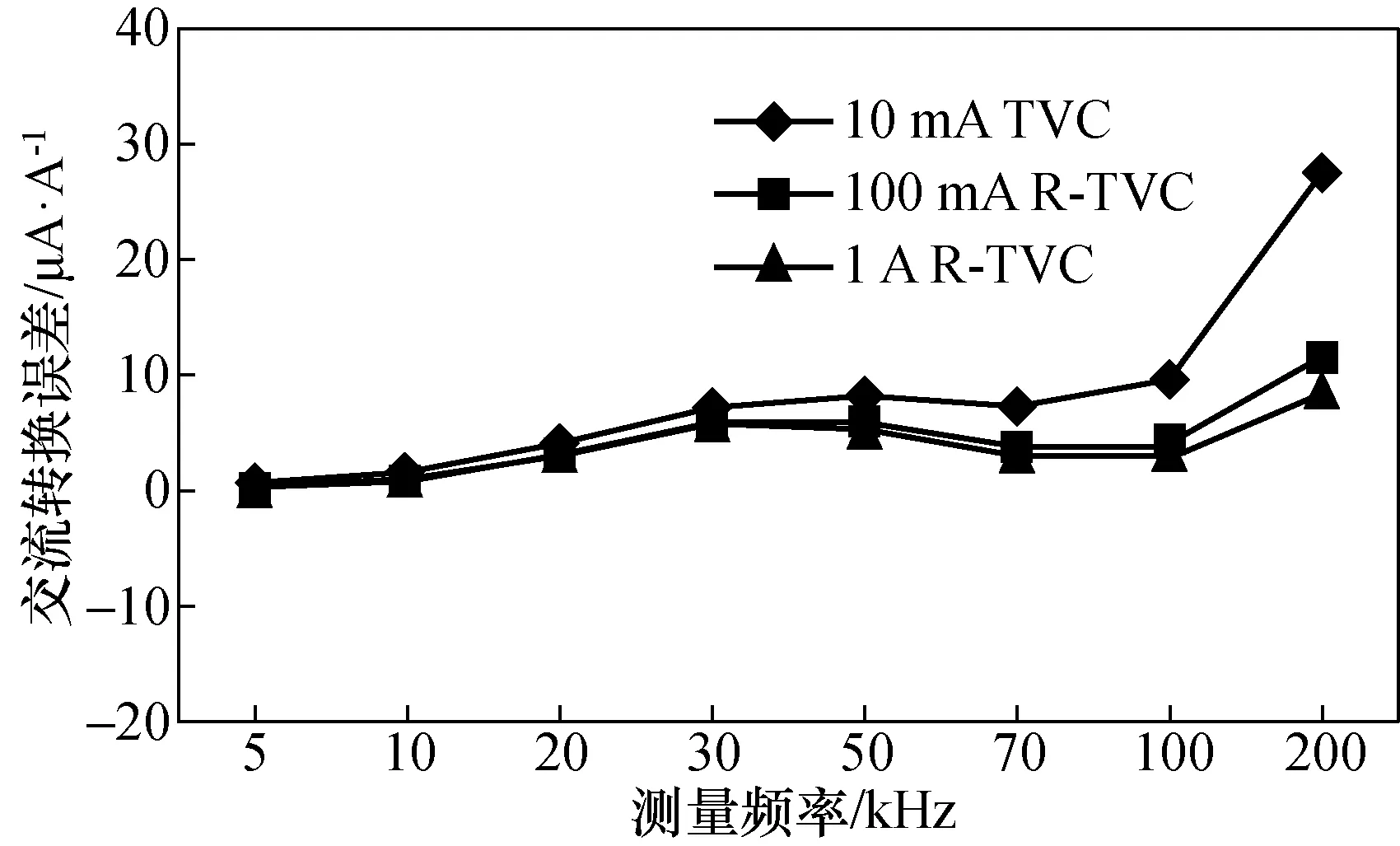
图5 串联模式下泄露电流影响误差Fig.5 Measurement results of leakage influence at in-series connection mode

由图5可以看出：当2个并联TVC和分流器组合之间进行比较时，在频率低于30 kHz,这种泄露电流影响小于10 μA/A；随着频率的增加，这种影响越为明显。考虑到串联连接模式下的泄露影响，采用基于二进制电抗分流器实现分流器和热电变换器组合之间共地比较测量；同时，在串联连接模式下采用换臂法来减少这种泄露影响。文中采用电抗分流器和换臂两种不同方法实现对热电变换器和分流器组合之间的相互比较，测量频率为5～200 kHz,测量电流为10 mA～1 A。

图6 采用两种方法比较热电变换器Fig.6 Comparison results between two TVCs based on two different measurement methods

2个热电变换器在10 mA测量电流下进行相互比较，结果见图6。由图6可以看出：二进制电抗分流器和换臂两种不同测量方法在频率200 kHz以内所得到的实验结果具有很好一致性；同时，这两种方法也很好地减少了泄露电流所引起的测量误差，在200 kHz频率下2个热电变换器交流转换误差优于 4 μA/A。

基于二进制电抗分流器和换臂两种不同测量测量方法也实现了100 mA和1 A分流器并联热电变换器组合的相互比较。

图7为2套100 mA和热电变换器组合采用两种不同方法，在5～200 kHz频率范围内的测量结果。实验结果表明:两种不同方法在10 Ω负载下一致性优于2 μA/A；同时2套分流器和热电变换器组合在200 kHz频率范围内频响特性优于5 μA/A。

图7 两种方法比较100 mA分流器和热电变换器组合Fig.7 Comparison results between two 100 mA shunt-TVC combinations based on two measurement methods

图8为2套1 A和热电变换器组合采用两种不同方法在5～200 kHz频率范围内的测量结果。实验结果表明:两种不同方法在1 Ω负载下一致性优于3 μA/A；2套分流器和热电变换器组合在200 kHz频率范围内频响特性优于6 μA/A。

图8 两种方法比较1 A分流器和热电变换器组合Fig.8 Comparison results between two 1 A shunt-TVC combinations based on two different measurement methods

6 测量不确定度分析

基于二进制感应分流器实现不同分流器和热电变换器组合之间相互比较，主要不确定度分量来自于热电变换器自身输出热电势的漂移影响u(δshift)、二进制电抗分流器自身比例误差所引起的测量影响u(δBICD)、二进制电抗分流器两路输出电流受负载不平衡所引起的测量误差u(δloads)、分流器和热电变换器组合在不同频率下的泄露电流影响u(δleak)、纳伏表测量输出热电势影响u(δmeter)及测量标准偏差u(δA)。结合各个测量不确定度分量，表2给出了基于二进制感应分流器方法实现热电变换器及分流器组合之间共地比较测量的不确定度。

由表2可以看出，测量不确定度主要成分来自二进制电抗分流器的两路电流之间的比例误差及其两路电流在不同负载下受负载不平衡所引起的影响。二进制电抗分流器两路电流比例关系在负载平衡下校验的比例误差优于1 μA/A;在负载为1%不平衡时，两路电流比例误差在200 kHz频率范围内优于2 μA/A。热电变换器输出热电势随时间漂移影响将采用4次测量方式，从而很好减少这种漂移影响。容性泄露电流影响在这种共地测量模式下，由于两个支路具有较好的对称性，从而很好地消除了这种测量影响。另外纳伏表及测量标准偏差也通过实验进行分析评估。

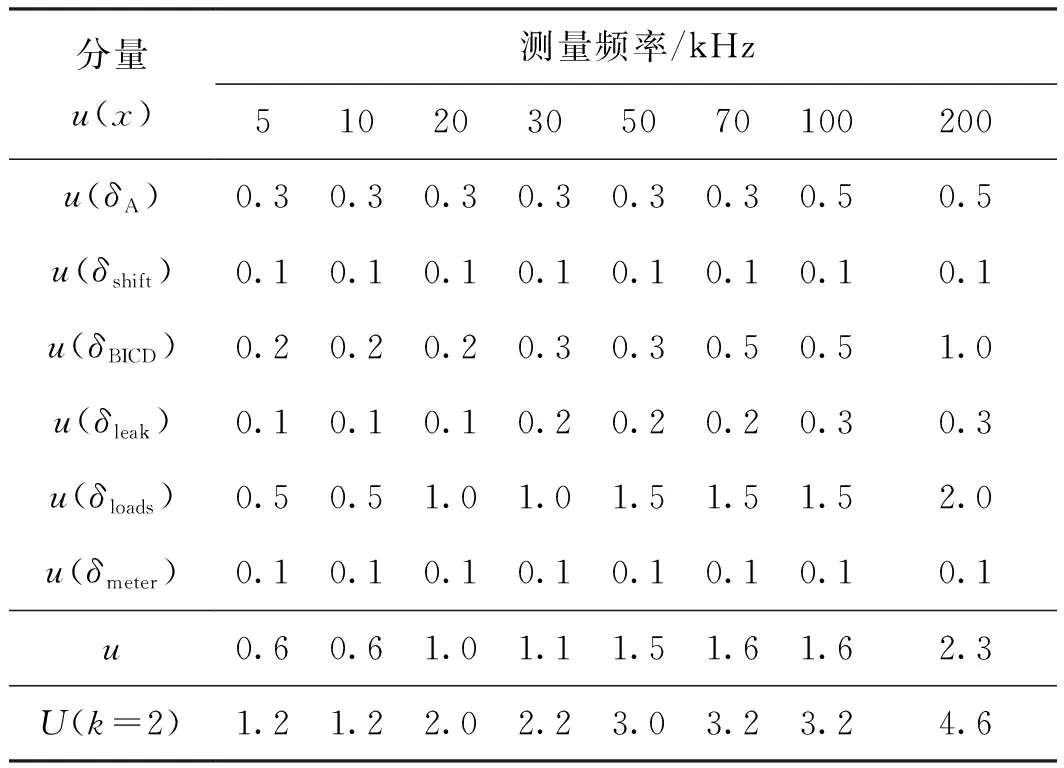
表2 热电变换器和分流器组合不确定度分析Tab.2 Uncertainty for comparing two shunt-TVC combinationsbased on the BICD method μA·A-1

7 结 论

本文提出了一种基于二进制电抗分流器实现热电变换器和分流器组合之间共地测量的方法，并采用这种方法对3种不同分流器和热电变换器组合在10 mA～1 A电流下进行了测量。实验结果表明：基于二进制电抗分流器方法，热电变换器和分流器组合在200 kHz频率范围内一致性优于6 μA/A；同时与串联模式下采用换臂法测量进行相互比较，2种方法的一致性优于3 μA/A。