沉船扳正封尾力计算
(广州打捞局,广州 510260)
为了使沉船在打捞出水后能够正浮或者装载至驳船,通常需要在打捞出水前对沉船进行扳正作业,即在水下将沉船恢复至正沉状态,见图1。使用外力进行扳正时需要对扳正钢丝绳一端进行固定,即所谓的封尾。封尾有将钢丝绳固定在沉船船体或固定在起重船吊钩上2种形式。
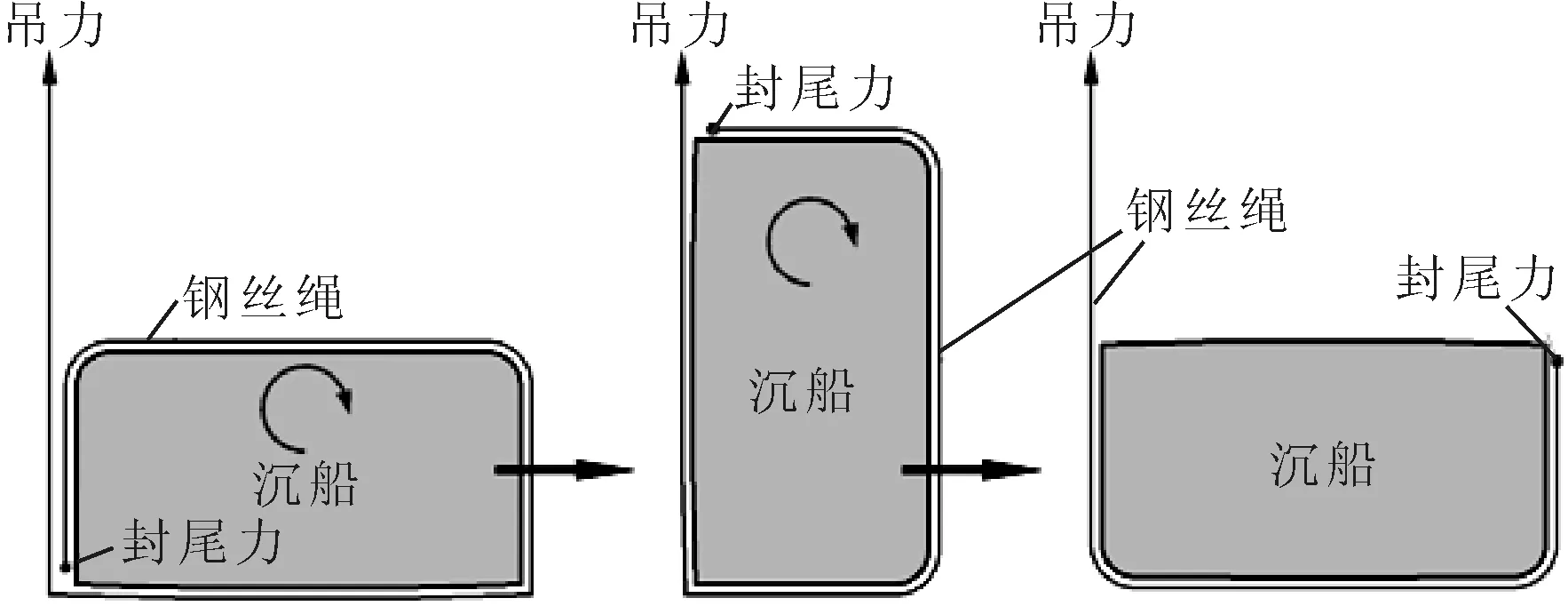
图1 沉船扳正过程示意
扳正封尾力的计算是保证沉船扳正安全与成功的重要保障。传统的扳正封尾力计算是利用规则圆柱体进行近似计算,用该方法计算布置在沉船平行中体钢丝绳的封尾力误差较小,但对于船体线型变化较大的船体,计算封尾力误差较大。为此,根据钢丝绳特性,建立简化的钢丝绳有限元等效模型,并通过理论计算及ANSYS有限元分析两种方式对圆柱体绕绳封尾力进行计算。
1 圆柱体的封尾力理论计算
摩擦力只与摩擦系数及正压力有关,本文所有摩擦系数默认取0.15。
如图2所示,钢丝绳绕过表面光滑的固定圆柱体,圆柱体半径为R,钢丝绳接触圆弧角度为α,圆心为O点,两端接触点及中间接触点分别为A、B及M,所受拉力Fn及封尾力F0均为F。钢丝绳线张力为k。

图2 圆柱体模型
圆柱体接触区域钢丝绳张力在OM圆弧上的总和为
(1)
根据钢丝绳受力均衡,则钢丝绳受力为
(2)
因此
(3)
在圆柱体存在摩擦力的情况下,假设接触圆弧长度为l,且被分成n等分,每段小圆弧分布受前后端圆弧拉力Fi+1、Fi及摩擦力fi影响。
Fi+1=Fi+fi=Fi+μk·Δl=
(4)
因此
(5)
2 建立有限元模型
如果按照钢丝绳实际结构建立有限元模型,需要花费大量的计算资源进行长时间的计算,这对于应急抢险的救助打捞工程明显是不现实的。因此,需要建立一个等效的钢丝绳有限元模型来模拟救助打捞中的封尾力计算。钢丝绳受力工程中主要体现受拉及受压,其抗弯性能较差,本文主要计算因摩擦力作用后的封尾力,可对钢丝绳有限元模型进行简化。
采用ANSYS板单元模拟钢丝抗压特性并由板单元进行摩擦力的计算;为模拟钢丝绳的容易弯曲的特性,将板单元的厚度及弹性模量数量级降低,使板单元产生的弯矩对计算结果影响不大;同时因为接触面积对摩擦力的影响不大,因此,尽量降低板单元宽度至有限元单元的宽度。钢丝绳的抗拉特性由板单元钢丝绳加入link180单元进行模拟。板单元与link180共享单元节点。钢丝绳有限元简化模型见图3。
按照以上建模思路,假定钢丝绳的接触宽度为10 mm,其中板单元厚度取1 mm,弹性模量取2.1 GPa;link180弹性模量取210 GPa。该模型模拟直径为76 mm的8×37+IWR钢丝绳,为了使有限元模型受力后的伸缩量较为接近实际,因此link180的面积取2 267 mm2。该模型在受600 kN拉力时,伸缩量为0.066%。有限元模型伸缩量见图4。

图3 钢丝绳有限元简化模型

图4 有限元模型伸缩量
根据此简化后的有限元模型计算包角分别为90°及180°的圆柱体钢丝绳封尾力。计算结果见表1。

表1 2种工况下圆柱钢丝绳封尾力理论计算与有限元计算结果对比表
1)包角为90°的圆柱体钢丝绳封尾力有限元分析。如图5所示,圆筒上下边为固端,钢丝绳B点与圆筒共享节点并设定节点位移为零,钢丝绳与圆筒之间采用有摩擦接触,摩擦系数为0.15,C处拉力与圆筒相切且值为600 kN,有限元模拟计算结果B处的封尾力为480 kN。90°包角圆柱钢丝绳有限元模型见图6。

图5 90°包角圆柱钢丝绳边界条件
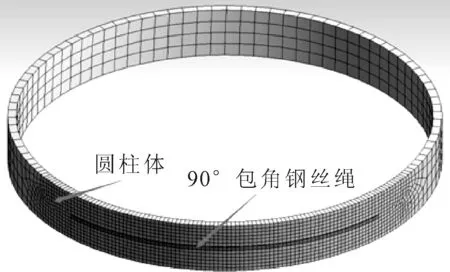
图6 90°包角圆柱钢丝绳有限元模型
2)包角为180°的圆柱体钢丝绳封尾力有限元分析。
如图7所示,圆筒上下边为固端,钢丝绳C点与圆筒共享节点并设定节点位移为零,钢丝绳与圆筒之间采用有摩擦接触,摩擦系数为0.15,B处拉力与圆筒相切且值为600 kN,有限元模拟计算结果C处的封尾力为380 kN。有限元模型见图8。

图7 180°包角圆柱钢丝绳边界条件

图8 180°包角圆柱钢丝绳有限元模型
结果表明,简化的钢丝绳有限元模型能够满足工程计算精度。在计算钢丝绳与船体接触时同样采用此有限元模型计算,因为有限元计算原理相同,因此计算结果同样满足计算精度。
3 算例分析
沉船扳正封尾力计算主要包括钢丝绳与船壳接触的摩擦力和转角处的摩擦力。根据公式(5)可知摩擦力与圆柱体的半径无关,因此,无弧形过度的转角处摩擦力(例如,甲板板与舷侧板处的摩擦力)可根据式(5)利用相对应钢丝绳包角进行计算;与外船壳接触的摩擦力则利用有限元进行分析。
以138 m长散货船在侧翻90°状态下1/2站处钢丝绳扳正封尾力计算为例(见图9),假设吊力设计为600 kN,摩擦系数取0.15。下例将分别计算转角处及船体外壳的钢丝绳张力衰减系数,最终根据总的衰减系数计算封尾力。

图9 138 m散货船型线图及1/2站计算示意
1)无圆弧转角处的钢丝绳衰减计算。图9中1/2站船体与钢丝绳包角为120°,根据式(5)计算得钢丝绳吊力在甲板转角处的钢丝绳张力衰减系数k1=0.73。
2)船体外壳钢丝绳衰减计算。钢丝绳与船壳接触的摩擦力通过有限元模型进行计算,考虑到船体为对称结构,因此只建一半船体有限元模型,见图10。

图10 钢丝绳与船壳接触摩擦力计算边界条件及有限元模型
在给定C处拉力为600 kN时,B处的封尾力为49.89 kN。
因此整段船壳外板的衰减系数k2为0.67。
3)封尾力计算。根据公式(7)、(8)可得总衰减系数k=k1k2=0.489。
因此封尾力F0为
F0=F·k=600 kN×0.489=293 kN。
如果计算如图9中类似18站所示钢丝绳与船体部分不接触时,可将钢丝绳分段进行有限元模拟计算,将钢丝绳在与船体不接触的地方断开分别计算后与折减系数相乘得出总的折减系数,最终计算出封尾力。
4 结论
通过理论分析推导圆柱体钢丝绳的封尾力公
式,并根据钢丝绳在接触摩擦计算中体现的特性简化钢丝绳有限元模型,不仅加快了建模和计算速度,同时可以用于分析复杂船壳的钢丝绳接触问题。通过结合理论公式计算结果,该钢丝绳简化能够满足工程计算精度,为救助打捞工程安全施工提供技术支持。

