适应情景变化的协同推荐算法

张忠海，夏 宇,2*，杨舒波

(1. 江西师范大学地理与环境学院，330022，南昌；2. 鄱阳湖湿地与流域研究教育部重点实验室，330022，南昌)

0 引言

信息过载使用户难以快速地从现有信息中获取感兴趣的信息[1]，推荐系统在极大程度上缓解了这个问题。现有研究表明，融合情景的推荐结果明显优于非情景信息的推荐结果[2-3]。移动定位技术的发展，使得用户的位置信息、身份信息、周围的人以及这些信息的变化很容易获取，并以位置为核心，这构成了最初的情景信息[4]。Brown认为时间、温度和季节等也会对用户产生影响[5]，此后用户的情绪[6]、用户感兴趣的对象[7]以及身体状况[8]等被加入到情景信息。随着情景维度的增多，不同用户对同一项目的评价可能在2个完全不同的情景下完成，这种情况下直接使用经典协同推荐很容易得到错误的用户相似度，低维的个性化推荐算法无法直接适用于高维的个性化推荐。为了解决这个问题，一些研究从情景预过滤的角度分析，主要在于进一步提高用户相似度的精度，如在情景相似的前提下，计算用户相似度[9-10]；对项目的内容特征进行聚类[11-12]；或以不同的权重综合考虑多种相似度[13-14]。这些研究在预过滤的前提下进行协同推荐，使用户的可用数据急剧下降，冷启动问题更加突出，对于用户数据原本较少的领域，如旅游领域，算法难以适用，对用户偏好的研究不足，无法动态地适应情景变化。近年来对情景建模的推荐算法研究逐渐增加，对语义分析和情景的影响考虑得更加细致,包括用户情感方向和特殊情景下对用户行为的抑制等[15]，建模过程复杂，用户偏好的改变或兴趣漂移，会使算法成本显著增加，情景建模需要大量文档数据，模型精度依赖于文本解析算法的精度，算法更适用于基于属性的个性化推荐。基于上述分析，本文提出一种适应情景变化的推荐算法，在经典协同推荐的基础上，通过计算用户对情景的效用，以情景效用补偿情景变化的影响，动态地适应情景变化，不用进行复杂的建模和计算，不会降低数据的利用率，算法适用性强。

适应情景变化的协同推荐算法分为情景效用评价和评分预测2个阶段：情景效用评价发生在推荐前，对每一个具体用户，计算用户对情景的效用，量化用户对情景的偏好；评分预测时比较当前情景和历史情景的差异，在经典协同推荐算法[16]的基础上，通过情景效用调整用户在当情景下对目标项目的评分。本文引入用户情景效用概念，给出计算情景效用的有效方法，并提出了一种适应情景变化的协同推荐模型和算法。实验表明，本算法可以动态地适应情景变化，并能有效的提高推荐质量。

1 基于情景效用评分的协同推荐

行为学认为，人自身的状态和所处环境状态的相关参数都被考虑在内之后，人的行为具有相对稳定的偏好[17]。可以通过对数据统计分析，定量研究影响用户行为的因素，来把握用户的行为[18-19]，这说明用户的行为是可以度量的[20-21]，这种行为往往反应用户的偏好。经典的协同推荐并不分析用户偏好，仅在计算用户相似度后，根据公式将满足要求的用户项目推荐给目标用户，但此时的情景与当时的情景可能有很大不同，直接推荐可能并不符合用户需求，需要根据情景差异进行调整。事实上，经典协同推荐只考虑了用户对项目的兴趣度，并没有考虑情景变化对用户的影响。

1.1 情景和效用

不同领域对情景缺乏统一的表达，本文从现有研究中选择项目情景、用户情景、商业情景、社会情景、时间情景、物理情景和网络情景等作为本文考虑的主要情景，并将每种情景划分为不同的子情景，按层次树结构进行组织，如图1。情景层次化有助于情景的扩展，能够更好地适应不断变化的上下文环境。

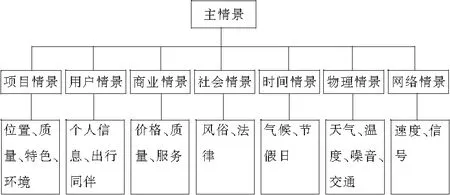
图1 情景层次树模型

将情景(指子情景，下同)作为影响用户评分的单位，同一情景的具体情况不同对用户的影响也有差异，如当一些游客选择旅游景点时，距离的远近可能对游客产生不同程度的影响。考虑要计算用户对情景的效用，所选取的情景应是具有一般性、稳定性的主要情景，如项目的位置、价格和商业环境的服务、质量等，进一步将所考虑的情景细分为若干个类别，不同的类别对用户的影响是不同的，对子情景进行分类，如表1。对于每个用户，从表中选取影响该用户的若干个主要情景。

表1 子情景分类

本文引入经济学中的基数效用论，用效用度量用户消费的满足程度。偏好的差异导致效用的差异，可以通过用户效用来反映用户偏好。在推荐领域，效用可以视为用户对项目的评分，由项目和项目所处情景决定，用户的最终评分表现为用户对项目效用和对各情景效用的叠加，当各分效用已知时，就可以求出用户对具体项目的总效用。

1.2 情景效用评价

设项目i的所有情景分类为Ti={ti,1,ti,2,…,ti,j},ti,j= {0,1}，用户对所有情景下不同分类的效用为kj= {k1,k2, …,kj}。根据基数效用论，用户对项目的效用可以用如下公式表示：

Si=∑nj=1kjti,j

(1)

式中：ti,j取值1或0，表示存在或不存在，同一时间一个情景下最多只能有一个分类存在；kj表示用户对ti,j的效用，Si表示用户对项目i的总效用，即评分。如用户在选择旅游景点时主要考虑距离和价格2个情景，并且用户对距离的效用为近(2)、一般(1)、远(0)，对价格的效用为低(3)、一般(2)、高(1)，对其它情景效用为0，则用户对距离近且价格一般的景点的总效用为：2×1+1×0+0×0+3×0+2×1+1×0+0×0+…=4。

当i=1,2,3,…,m时，与线性最小二乘法的基本公式一致:

∑nj=1Xi,jβj=yi

(2)

式中：m表示等式个数，n表示未知数个数，m>n，通过m个实测值可以求得使残差平方和最小的β值，即可以根据m条用户数据求得用户对情景的效用。

1.3 基于情景效用的评分预测

本文在经典协同推荐基础上进行改进，将算法分为预测阶段和调整阶段。预测阶段使用经典算法进行预测，首先根据所有用户和项目构建用户项目-矩阵，然后根据用户-项目矩阵计算用户之间的相似度，最后根据公式(3)计算出用户对项目的预测值，本文相似度计算采用皮尔逊相关系数。

用户u对项目i的评分预测公式如下：

(3)

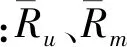
计算出用户对项目的评分后，进一步考虑当前情景与历史情景的差异，调整用户对项目的评分。分析公式(1)，对于相同项目i，不同的情景t和c有：

Si,c=Si,t+∑nj=1kj(cj-tj)

(4)

式中：Si,t表示情景t下用户的总效用；Si,c表示情景c下用户的总效用。

适应情景变化的推荐算法：

输入：目标用户数据，其他用户数据；

输出：目标用户的推荐集；

伪码描述：

1: Input current user data (u,i,c)；

2: forMitemi%M表示参与效用计算的数据量；

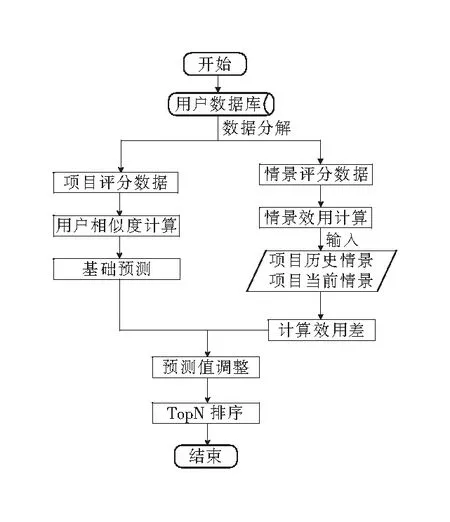
图2 适应情景变化的协同推荐

3: build I×C matrixC(i,c)；%构建项目-情景矩阵；

4:build U×I matrixR(u,i)；%构建用户-项目矩阵；

5:for all itemsi；

6:User utility:k(u,j)=pinv(C(i,c))*R(u,i)'；%j表示用户效用的个数；

7:for all neighbor usersb；

8:for common itemsi；

9:sim(a,b)=

10:forallitemsi；

11:ifsim(u,i)>δ%δ表示相似度阈值；

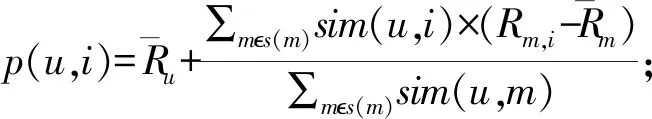
13:forallp(u,i)；

14:S(u,i)=P(u,i)+∑j=1k(u,j)×(cj-tj)；

15:returnTopN(S(u,i))。

2 实验分析

实验的硬件环境为Inter(R) Core (TM) i5-7300HQ CPU @2.50GHz 2.50GHz，8G内存。软件环境为Windows10，Matlab2017a，算法使用Matlab脚本语言编写。

2.1 实验数据和评价指标

算法通过解超定方程的方式来拟合用户的情景效用，用户数据必须大于所考虑的所有情景类别个数。采用模拟数据的方式进行仿真实验[22-24]可用于评价复杂情景感知推荐算法[25]，能避免实际数据中存在的稀疏性和冷启动等问题，更好地验证算法的有效性。考虑到一些领域用户的历史数据量相对较少，为了保证用户有足够的数据，选取的主要子情景数量要适中。不同领域，用户所关注的情景大不相同，故实验考虑5个较普遍的情景，每个情景分为3个类别，共15个效用值。每个用户对情景的偏好和每个项目的情景类别用随机数函数产生，不同的用户所考虑的情景不同，为了能够统一表达，用户偏好可以为0，如User={p1，p2，p3，p4，p5}，pi的取值为[0,5]，Item={l1，l2，l3，l4，l5}，li的取值为[1,3]，通过公式(3)计算用户对项目的评分。共模拟1 000个用户和1 000个项目，每个用户从1 000条数据中随机选择40个项目进行评分，部分数据如表2、表3。文献[12]指出，当邻居数达到20时，推荐结果的精度，不会随邻居数量增加而提高，从模拟数据中抽取至少拥有20个邻居的用户进行实验。

表2 用户偏好

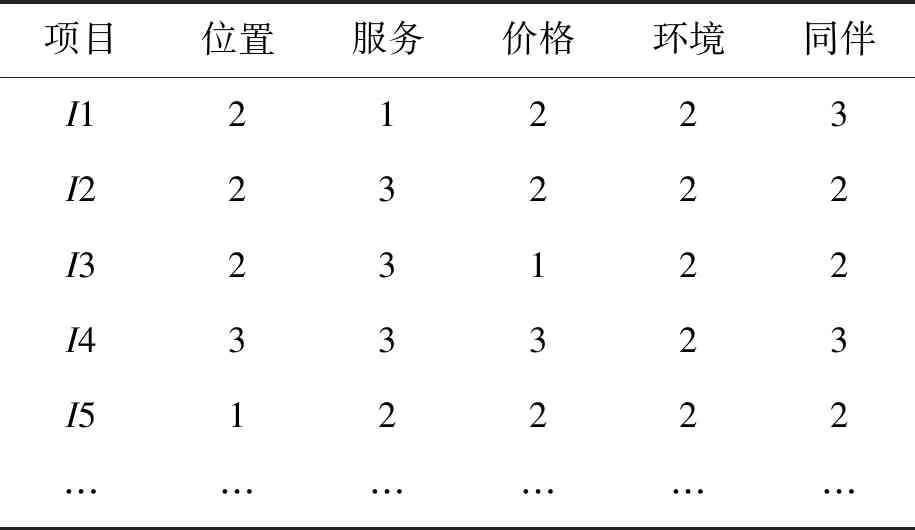
表3 项目情景类别

本文采用常用的平均绝对误差(MAE)作为度量标准，MAE值越小，准确性越高，设预测的用户评分集合表示为{p1,p2, …,pN}，对应的实际用户评分集合为{q1,q2, …,qN}，则平均绝对偏差MAE定义为：

(5)

2.2 实验结果

对1 000个用户的数据进行分析，选取其中334个符合条件的用户。对于每个用户，模拟1个项目情景作为历史情景，根据邻居的评分使用经典算法来预测目标用户的评分；模拟3个项目作为当前情景，为表现与历史情景的差异，设置1个项目情景与历史情景完全相同，1个项目情景明显优于历史情景，1个项目情景明显低于历史情景，计算用户的实际评分，部分数据如表4。

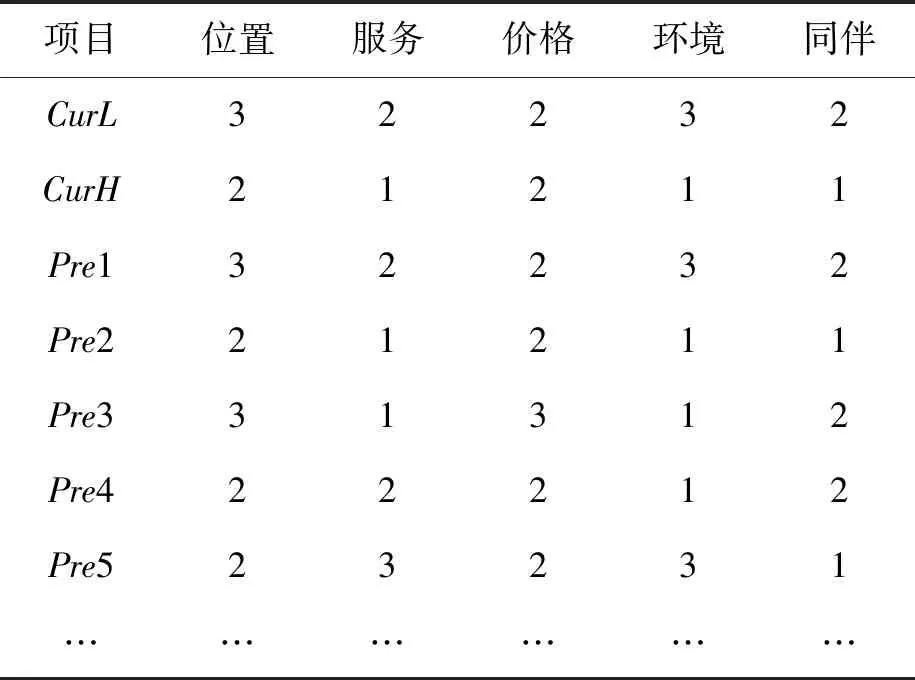
表4 当前项目与部分历史项目

首先使用经典协同推荐算法求基础预测值。分别计算3种情况的MAE，相同情景、不同情景1(优于历史情景)和不同情景2(低于历史情景)，重复实验10次，如图3。实验发现：当历史情景与当前情景相同时，经典的协同推荐算法有较高的推荐质量；当历史情景与当前情景差异较大时，经典推荐方法精度极不稳定，具有随机性。原因是，经典推荐方法假设历史情景与当前情景总是相同，但实际情况往往与此不同，而当历史情景与当前情景差异很大时，经典方法可能会给出错误的结果。图中横轴表示实验次数，纵轴表示MAE。

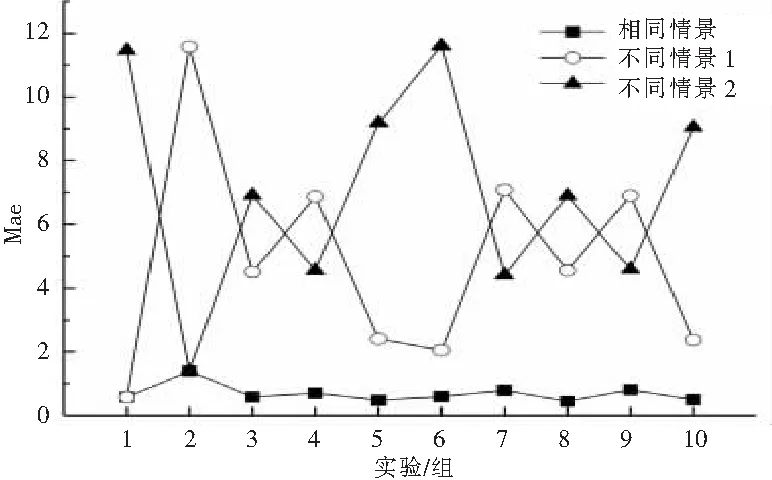
图3 经典算法不同情况下的MAE

然后计算用户对情景的效用。效用通过解方程求取，为了保证最终的推荐质量，需要保证用户对情景效用的精度。用M表示参与计算的用户数据量，本文考虑15个效用，故M≥ 15,取M等于15、20、25、30、35、40进行实验，使用历史数据的观察值进行调整，结果如表5和图4。研究发现，M越大时，精度越高，当M取40时，有较高的精度，实验最终取M=40。

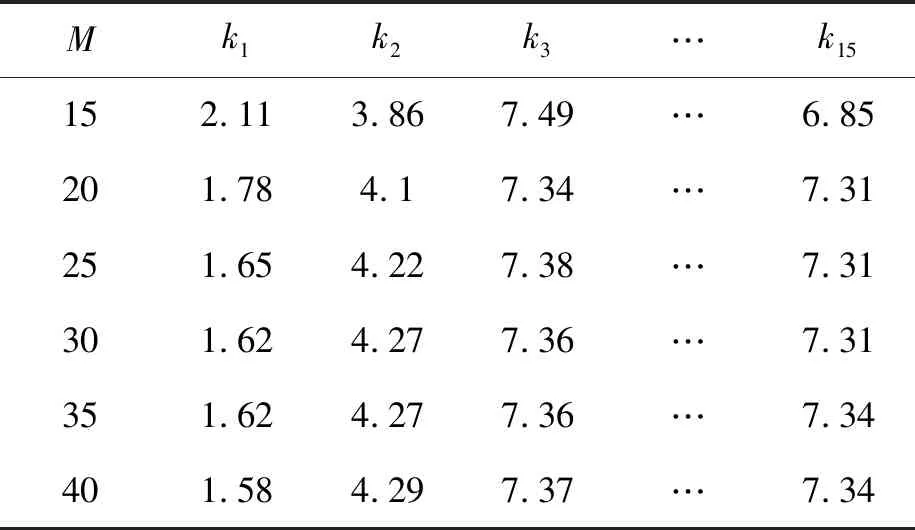
表5 某用户不同M值下的情景效用

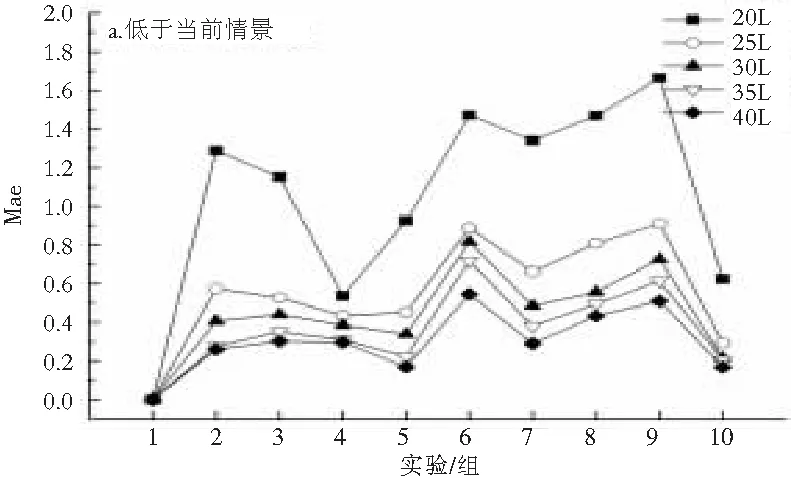
(a) 低于当前情景

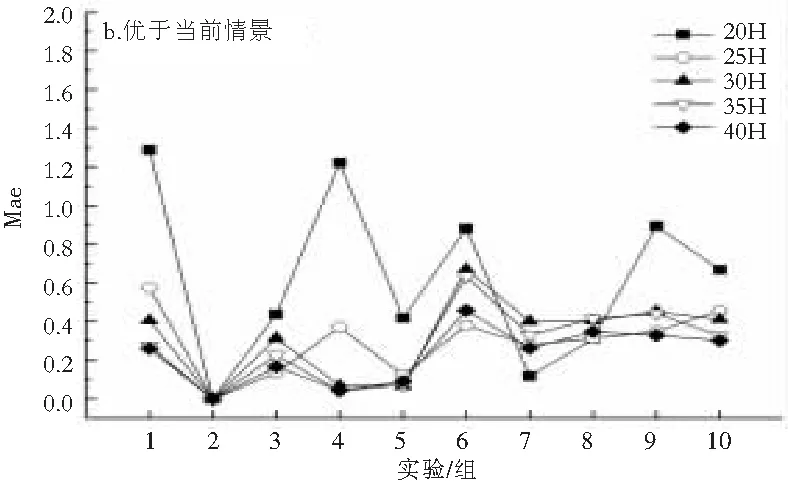
(b) 优于当前情景

最后对基础预测值进行调整。从图3可以看出，当历史情景与当前情景相差很大时，传统算法的推荐质量很低，但当历史情景与当前情景相同时，传统算法有较高的推荐质量。对图3中不同情景1和不同情景2的预测值根据情景效用进行调整，如图5。

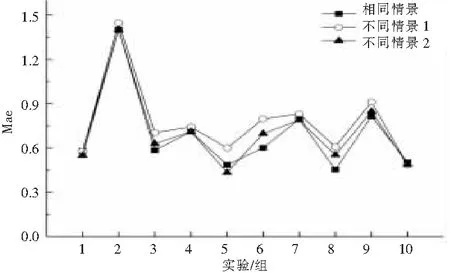
图5 预测值调整后的MAE

可以发现，不同情景的预测值调整之后的精度与相同情景下的预测精度十分接近，具有较高的精度。为了进一步证明本方法的有效性，取用户对项目的实测值进行调整，其中不同情景1的第1个项目不用调整，不同情景2的第2个项目不用调整，结果如图6。可以发现，当使用实测值进行调整时，预测精度进一步提高。结果表明，基础预测阶段的精度越高，调整后的精度越高。

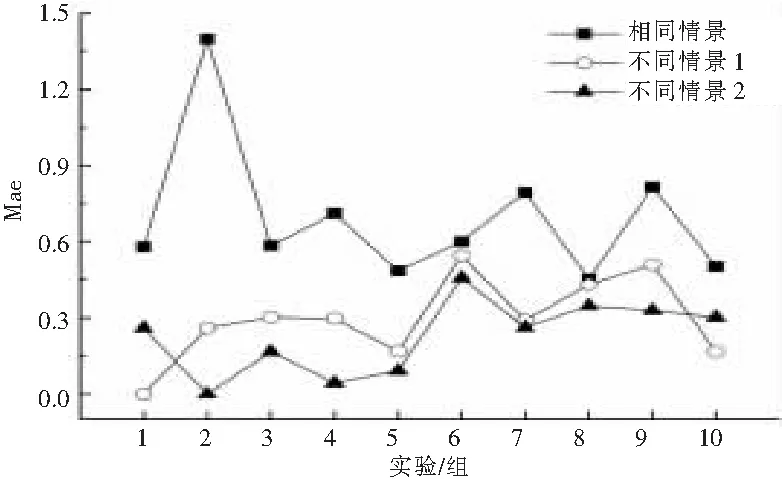
图6 真实值调整后的MAE

与文献[9]对比，当历史情景与当前情景不同时，本算法明显有更好的推荐质量，如图7。原因在于文献[9]使用平均值来表示用户对情景户偏好程度，这平滑了用户对情景的偏好，连续进行2次相似度计算，误差被积累，此外2次相似度计算使得计算量大大增加，相似情景下进行用户相似度计算会降低数据地利用率，使冷启动问题更加突出。

本文重点研究预测值如何调整以动态地适应情景变化。实验发现，当历史情景与当前情景相同时，经典协同推荐的预测值具有较高的精度。而实际生活中，历史情景与当前情景往往有所差异，因此考虑情景变化能够有效地提高推荐质量，可以发现，本文所提出的方法能够很好地适应情景变化；此外研究还发现，当预测阶段精度越高时，调整之后的精度越高；用户的情景效用计算只依赖用户历史数据，可以离线完成，在线阶段的时间复杂度增加O(N)；经典的推荐算法作为本算法独立的一个步骤，增加经典算法推荐质量的改进也可增加本算法的推荐质量。

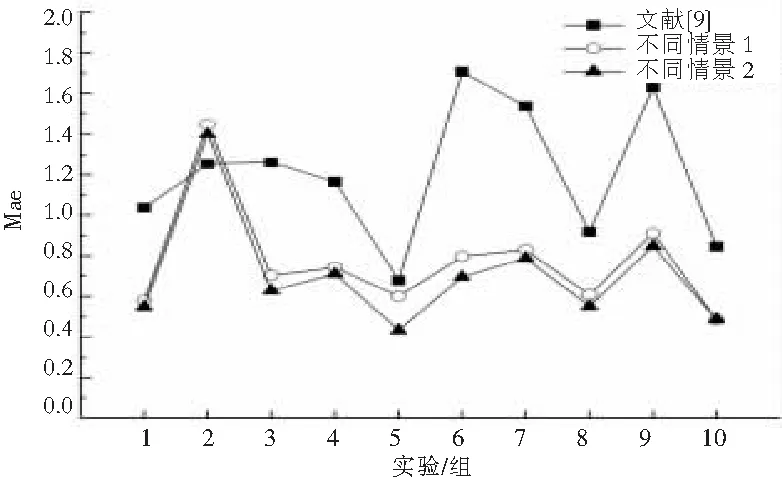
图7 适应情景变化的协同推荐算法与不同算法比较

3 结束语

经典推荐算法及众多改进算法无法适应情景的变化，很少考虑当前情景与历史情景间的差异，对所有用户都按照统一的规则进行分析。现有的个性化推荐策略采用前置过滤的方式，提高了推荐质量，却降低了数据利用率，使冷启动问题更加突出，并且无法动态地适应情景变化。本文在经典推荐的基础上，提出一种适应情景变化的推荐算法，将用户偏好转换为用户对情景的效用，通过用户对情景的效用来调整历史情景与当前情景不同时算法的预测值，使算法能动态地适应情景变化，在情景变化时，能做出合理的调整。本文给出的算法使用用户历史数据计算用户的情景效用，根据不同情景下的效用变化来调整预测值，理论上对不同的用户考虑不同的情景，算法能正确运行。实验表明了该算法的可行性和有效性，有助于提高推荐质量。