基于结构张量的自适应稀疏角度CT重建算法
张 萌,梁亚星,陈 燕,刘佳鑫,桂志国,,张 权,
(1. 中北大学 电子测技术国家重点实验室,山西 太原 030051;2. 中北大学 生物医学成像与影像大数据山西省重点实验室,山西 太原 030051;3. 中北大学 信息与通信工程学院,山西 太原 030051)
0 引 言
计算机断层扫描技术(Computed Tomography,CT)作为20世纪后期影像学的杰出代表,早已广泛应用于健康普查中[1]. 由于临床中常规剂量的CT扫描具有潜在的致癌风险,因此,“低剂量”已经成为CT研究的主流方向. 近年来,一些显著降低辐射剂量的研究主要聚焦于稀疏投影数据重建方面. 但稀疏重建由于投影角度的减少,导致了重建图像往往存在明显的条形伪影.
目前,解决该问题的一类主要方法是引入全变差(Total Variation,TV)稀疏性正则项作为约束条件[2-3]. 在此基础上,相关改进算法也得到了深入研究. 2009年Sidky[4]提出利用稀疏性更强的Lp范数来代替TV中的L1范数,获得了更加精确的重建图像; 针对传统TV正则项缺乏方向信息,易模糊低对比度边缘,2010年Jin等人[5]提出各向异性全变差(Anisotropic TV,ATV),同时利用图像稀疏性和边缘方向信息,在一定程度上来保护边缘; Bayram[6]等人于2012年提出一种方向全变差(Directional TV,DTV)图像去噪模型,通过增加某一主导方向的权重,显著增强该方向的边缘. 由于权重及方向参数是固定的,与ATV一样,该方法丢失了大量其他方向上的边缘信息; 为了克服该缺陷,Tao等人[7]利用估计的结构张量场计算图像方向结构,引入了多方向的边缘信息,进一步提高了重建质量.
鉴于此,本文提出了一种基于结构张量的自适应方向全变差稀疏角度CT重建算法,以下简称SADTVp.
1 背景知识
1.1 基于TV的CT图像重建模型
稀疏角度CT重建问题是一个典型的病态逆问题,常用图像f的全变差作为其稀疏正则项,其优化模型为
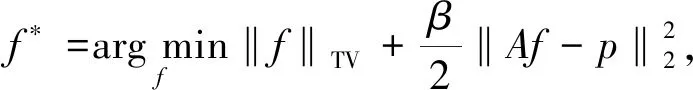
(1)
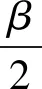
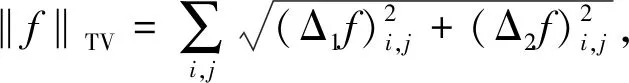
(2)
式中: Δ1和Δ2分别表示水平和垂直离散算子.
1.2 DTV正则项
将式(2)改写为
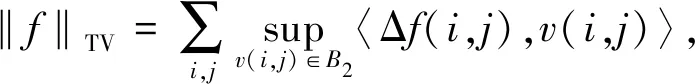
(3)
式中:B2是L2范数的单位球,Δf=(Δ1f,Δ2f)T.
传统TV模型中Δf的各分量表现为各向同性,缺乏方向信息,这将降低对低对比度边缘的检测能力. 为了克服这一不足,Bayram和Kamasak利用与图像梯度分布相对应的椭圆Eα,θ替换B2,提出了如下DTV正则项模型[6]
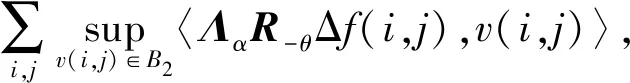
(4)
式中:Eα,θ=RθΛαB2,Rθ、Λα分别表示旋转矩阵与权重矩阵,用来刻画图像中特征结构的方向及该方向的权重[8],表达式为
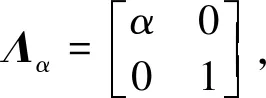
(5)
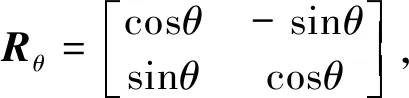
(6)
式中:RTθ=R-θ,θ为边缘方向与x轴夹角,α>1,表示沿边缘方向的尺度参数.
DTV模型中θ与α参数的选取是固定的,只对沿角度θ方向的边缘信息敏感,这将丢失大量其他方向的边缘信息.
2 本文算法
2.1 算法思想
为了能够充分利用各个方向的边缘信息,受文献[7,9]启发,本文引入结构张量,在重建过程中自适应地获取θ与α值.
结构张量常用来刻画图像局部区域的结构方向信息,与图像梯度相比,提取的边缘信息更加精确,其定义为
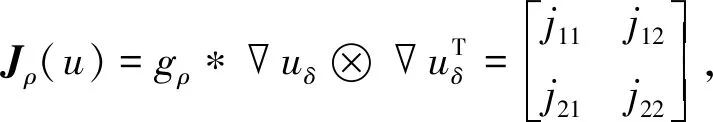
(7)
式中:uδ表示对图像进行参数为δ的高斯卷积,本文采用双边滤波代替高斯平滑,力求达到去噪与保留边缘的平衡;gρ为尺度为ρ的高斯核,引入局部邻域信息.
由于Jρ(u)是对称且半正定的二维矩阵,对图像边缘的方向估计和结构分析等可以通过对其进行特征分解实现[9]. 两个非负特征值为
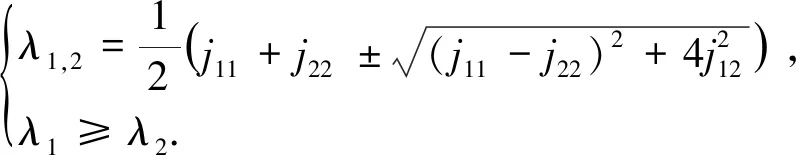
(8)
对应的特征向量为
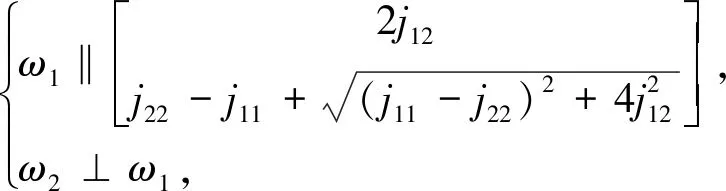
(9)
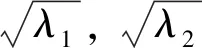
分析式(5)可知,当a≫1时,等价于仅沿角度为θ的边缘方向进行正则化,故本文将权重矩阵改写为
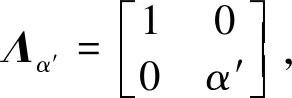
(10)
其中,0≤α′≤1.
基于结构张量的特点,本文将图像中每一像素点的θ和α′分别定义为
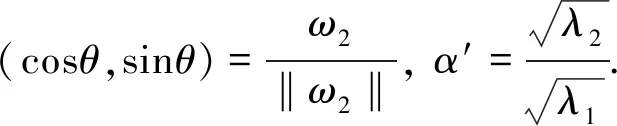
(11)
当处于边缘区域时α′≈0,图像仅沿边缘方向进行各向异性扩散; 处于平坦区域时α′≈1,图像进行各向同性扩散. 然而由于重建过程中的中间图像存在伪影及噪声,直接利用结构张量得到的初始边缘图通常较粗糙,不适合用来约束DTV正则化. 本文对初始边缘图进行边缘细化处理,剔除伪边缘点后,再更新式(11),即得到较准确的自适应参数.
2.2 算法模型
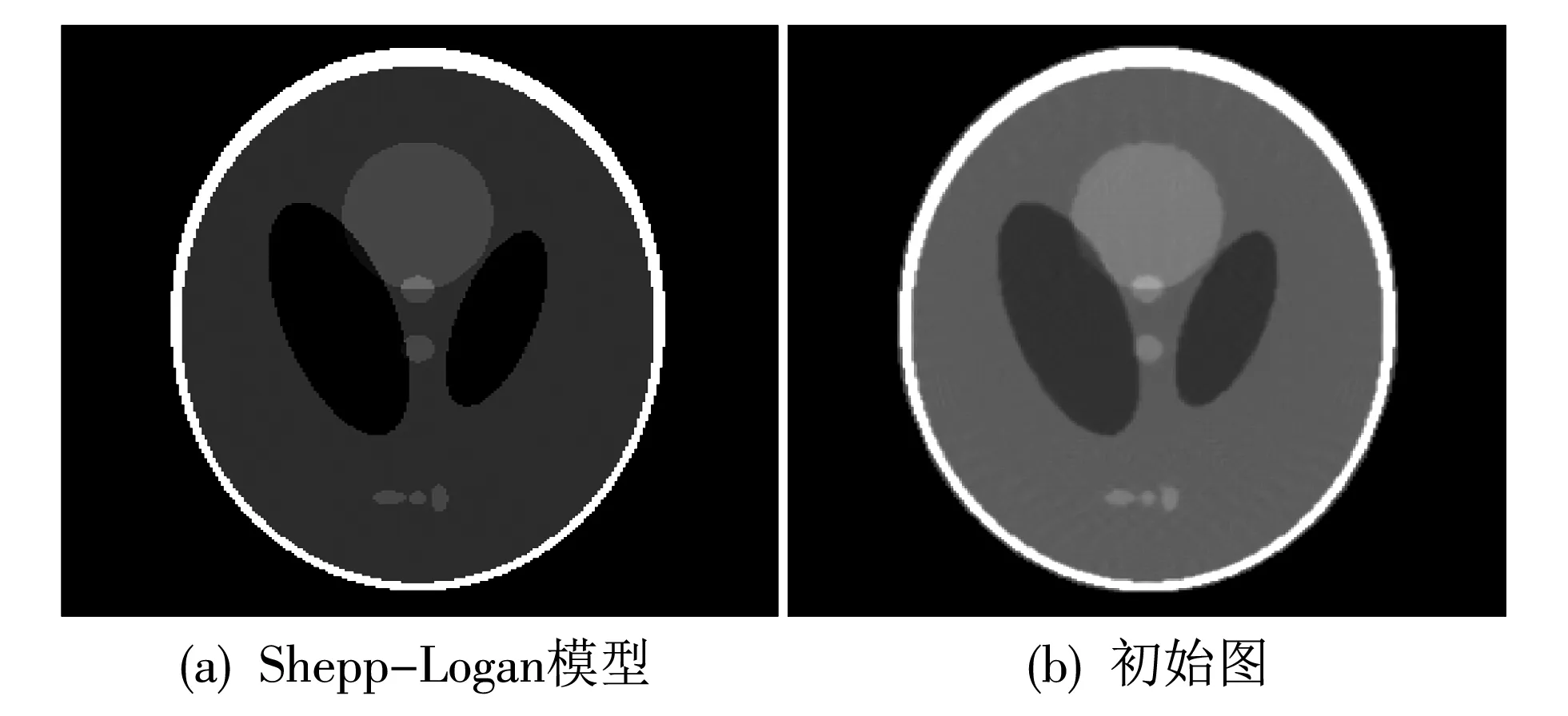
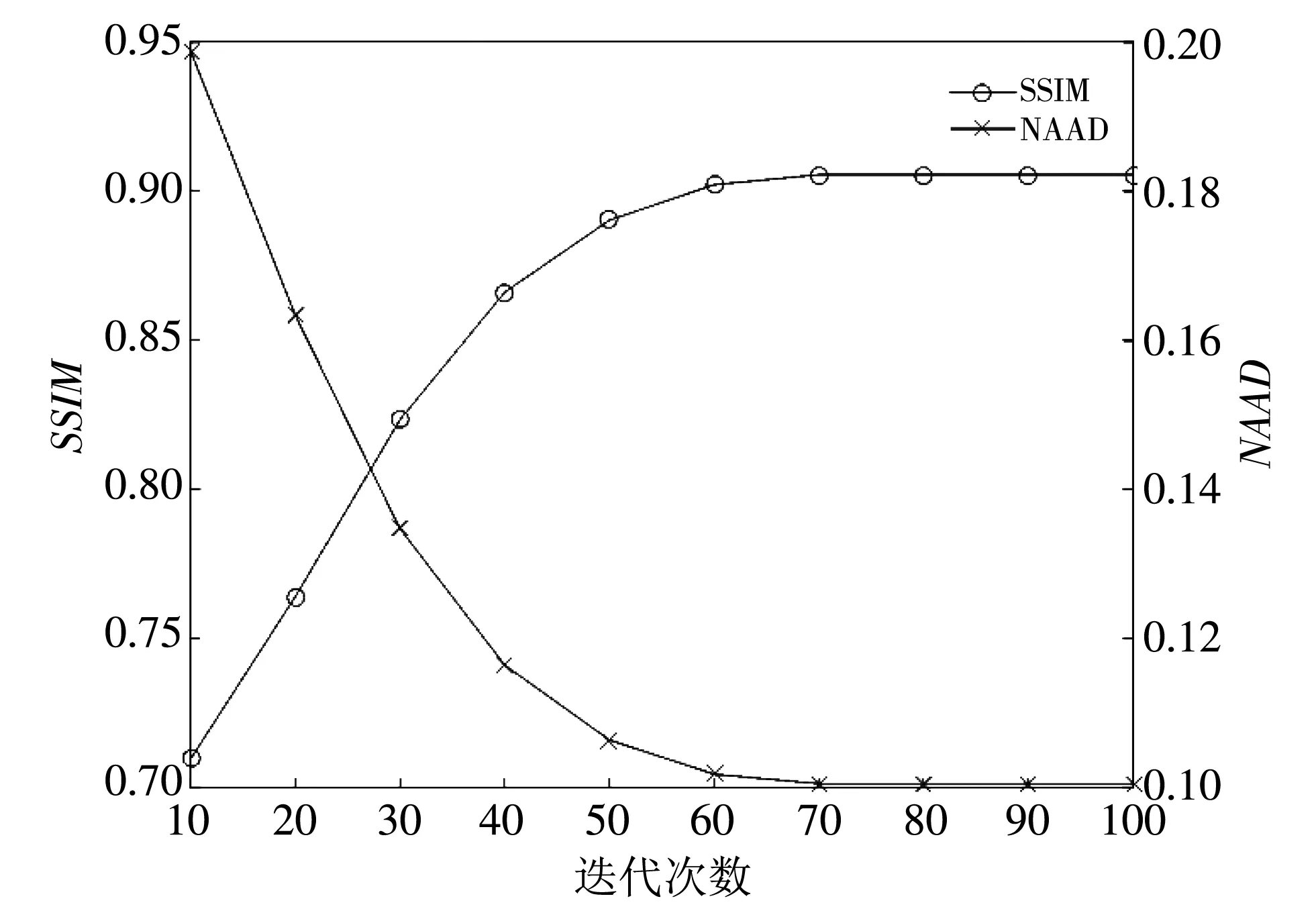
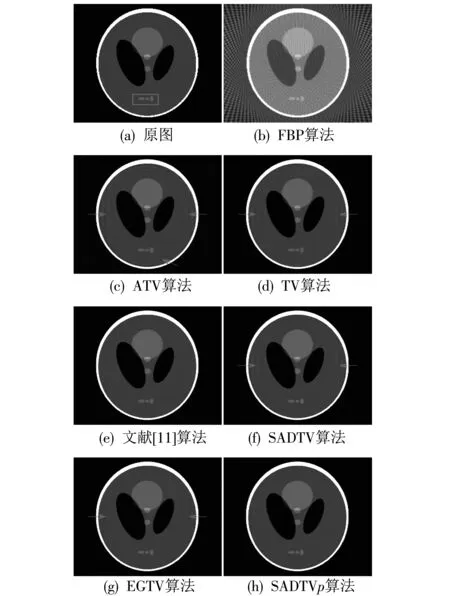
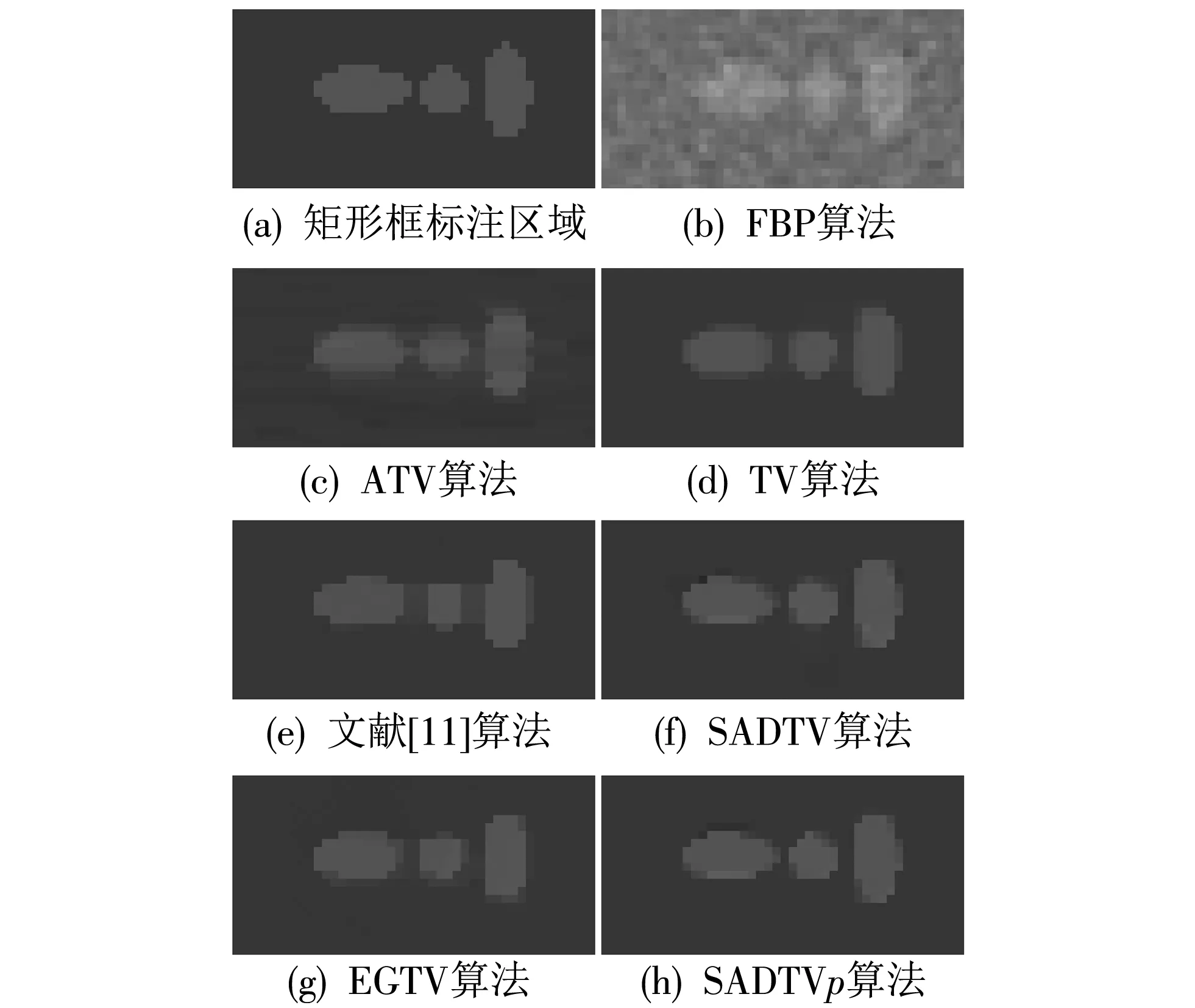
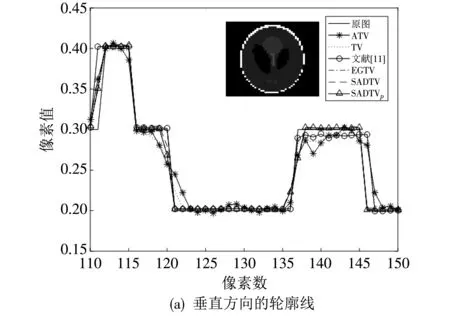
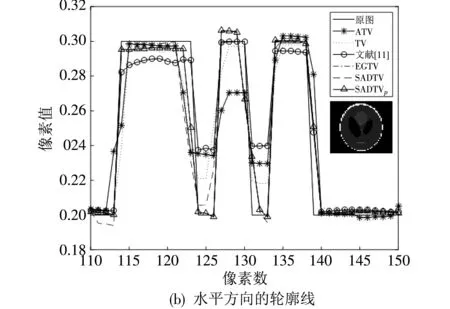
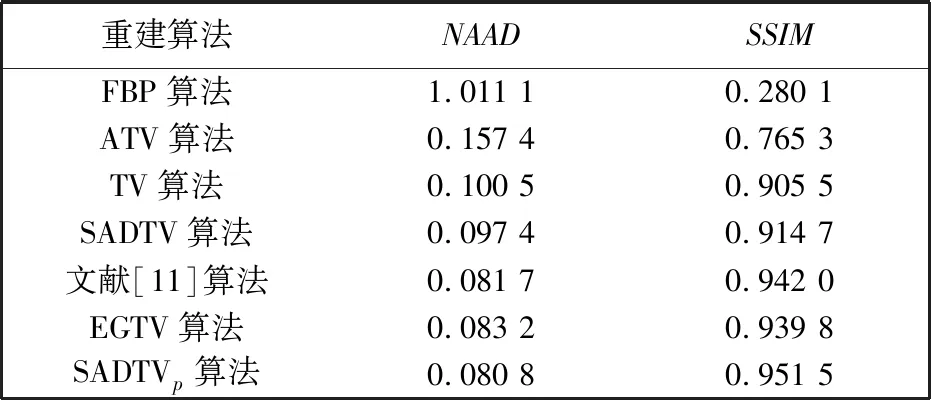
综合计算式(4)与式(6)~(11),同时考虑到,Lp范数(0 (12) 式中:f=[f1,f2,…,fN]T为图像矢量. 因此,重建模型为 (13) 对应的离散形式为 (14) 鉴于式(14)中的SADTVp范数正则项是非凸且非光滑的,本文基于宋洁等人提出的非凸模型求解算法[11],采用交替方向乘子法ADMM结合广义软阈值算法进行求解. 引入辅助变量wi=Λα′aiR-θaiΔif, 可以将式(14)转化为约束优化问题,即 s.t.wi=Λα′aiR-θaiΔif, (15) 其中,wi∈R2,i=1,2,…,N. 为了便于计算,令Λα′aiR-θaiΔi=Ti,则式(15)的增广拉格朗日函数可表示为 (16) 式中:λ为拉格朗日乘子;μ为惩罚参数. 利用ADMM最小化式(16)相当于在固定一个参数不变的情况下交替求解w与f两个子问题并更新λ的值[12-14]. 已知λ,保持f不变,最小化w可以表示为 (17) 式中:k表示迭代次数. 为解决上述Lp范数最小化问题,文献[15]提出一种广义软阈值函数, TGSTP(w,λ)= (18) (19) 已知λ值,保持w不变,f子问题求解可以表示为 (20) 显然,最小化f是一个最小二乘问题,此处利用梯度下降法求解. 首先计算目标函数的偏导数为 dk=β[AT(Afk-p)]+ (21) 从而得到 fk+1=fk-αdk, (22) 式中:α为下降步长. 综上所述,SADTVp算法步骤概括如下: 1) 输入初始图像f0,初始化参数λ0,w0,Rθ0,Λa′0,0 2) 利用式(19)更新w. 3) 利用式(22)更新f. 4) 更新λ=λ-μ(w-Tf). 5) 利用式(6)~(11)计算Rθ和Λα′,得到初始边缘图. 6) 对初始边缘图进行边缘细化. 7) 利用细化后的边缘图更新Rθ和Λα′. 本文采用图1(a) 所示的大小为256×256的Shepp-Logan头模作为实验对象. 在0°~180°范围均匀采集60个角度,探测器个数为260个. 实验中,在滤波反投影(Filtered Back Projection,FBP)重建过程中,利用零投影数据将空气区域修正为零,将非局部均值滤波后的重建图像作为迭代的初始图像f0,如图1(b) 所示. 图1 Shepp-Logan模型及初始图Fig.1 Shepp-Logan model and the initial image 为验证算法的有效性,选用FBP、 TV、 ATV[5]、 各向异性边缘检测引导的全变差CT重建算法EGTV[16]以及文献[11]中基于Lp范数的TV算法作为对比算法,在无噪声的情况下进行算法验证. 同时,将所提算法的Lp范数在p=1时定义为SADTV,参与对比分析. EGTV算法依据所在文献,采用凸集投影法求解,其余算法均采用ADMM方法求解. 经试验,相关参数设置如下: μ=26,β=0.6,ε=1×10-3,λ0=0,w0=0, 对比算法中的其他参数均参考其所在文献.Lp范数中p=0.7. 此外,为进一步评价所提算法的重建性能,采用归一化平均绝对距离判据NAAD、 结构相似度SSIM来定量评价各算法重建效果. (23) (24) 式中:ti,j和ri,j分别表示原始图像和重建后图像中第i行、j列的像素密度,μr、μt、δr、δt、δr,t分别表示重建后图像与原始图像的密度平均值、 标准差及协方差. 图2 为TV算法在60个采样角度下重建图像的NAAD、SSIM与迭代次数关系曲线图. 可以看出,迭代次数为70次以后曲线趋于平稳,因此迭代次数设定为70次. 图3 为不同算法在60个角度下迭代70次的重建结果. 同时,选取如图3(a)中矩形框标注的局部区域放大显示,如图4 所示. 图2 TV算法在60个角度下重建图像的NAAD、 SSIM与迭代次数关系曲线Fig.2 Iterative curves of NAAD and SSIM of images reconstructed by TV from 60 sparse-view 图3 不同算法在60个角度下迭代70次的重建图像Fig.3 Reconstructed images based on 60 angles after 70 times of iteration using different algorithms 图4 矩形标注区域的放大图Fig.4 Enlarged drawing of the rectangular label area 观察分析图3 及图4 可以发现,FBP算法重建图像含有大量条形伪影,边缘细节模糊; TV算法重建效果明显优于FBP算法,但在垂直方向含有少量伪影,同样存在边缘细节模糊的现象; ATV算法重建图像则呈现出垂直、 水平方向伪影; 与TV算法相比,文献[11]中算法、 SADTV算法和EGTV算法的重建质量均有所提升. 文献[11]中算法虽较好抑制了伪影,但相邻边缘仍有连接; SADTV算法和EGTV算法的重建图像的边缘清晰度有所提升,但垂直方向仍存在伪影. 相比而言,本文算法重建图像具有较好的一致性,边缘细节清晰,与原始图像的接近程度较高. 图5 为原图及六种迭代重建算法图像在水平、 垂直方向的剖面轮廓图. 图5 重建图像剖面轮廓对比Fig.5 Profile contour contrast of reconstructed images 由图5 可以看出,本文算法与原始图像轮廓最为吻合,尤其在边缘跳跃部分,改善了其他算法边缘钝化现象. 各算法迭代70次的质量参数见表1. 综合来看,七种算法中本文算法的SSIM最高,NAAD最小,算法的有效性得到验证. 表1 七种重建算法的质量参数对比 针对稀疏角度CT重建中全变差模型的局限性,提出将具有方向先验的方向全变差与更具稀疏性的Lp范数结合. 基于结构张量提取局部结构信息的优势,自适应地提取多个方向的边缘信息. 实验表明,与FBP算法、 TV算法、 ATV算法、 文献[11]中算法、 SADTV算法、 EDTV算法相比,所提SADTVp算法能有效抑制条形伪影且图像边缘轮廓完整清晰,可以提高稀疏重建性能. SADTVp算法重建效果依赖于结构张量边缘检测的精度,本文下一步将研究更优的边缘检测方法,提取更加精细的边缘,以进一步提升算法性能.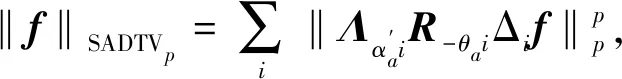
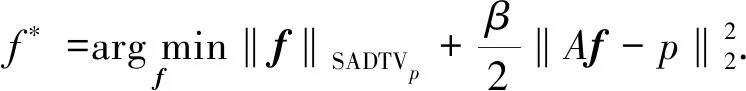
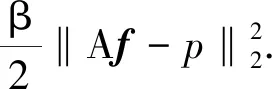
3 模型求解
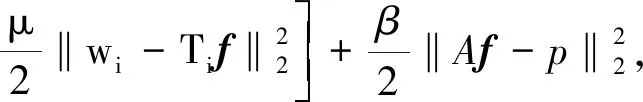
3.1 w子问题求解
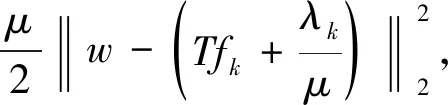
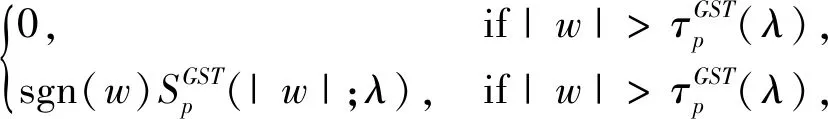
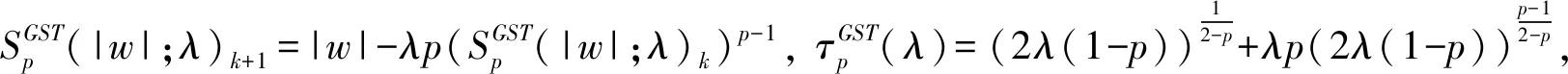
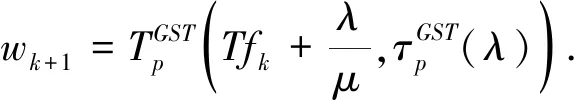
3.2 f子问题求解
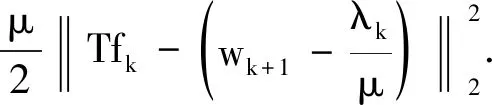
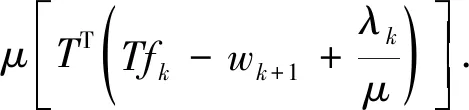
3.3 算法描述
4 实验结果与分析
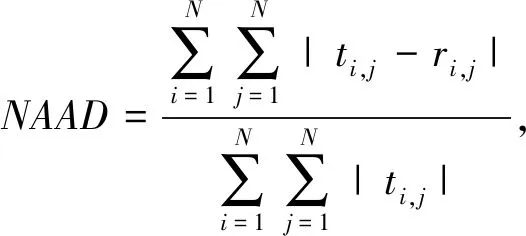
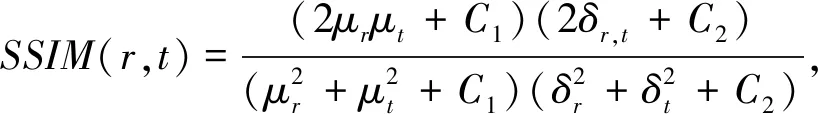
5 结 论

