高稳定度低温蓝宝石微波频率源设计
朱 玺 陈海波 黄 凯 高连山 王 亮
(北京无线电计量测试研究所,北京 100039)
1 引 言
低温蓝宝石微波频率源具有超高的短期稳定度及相位噪声,在航天、军事等众多领域有着广泛的应用前景[1-6]。在基础物理研究方面,其应用范围包括为原子喷泉频率标准提供本振、进行精密测量、服务甚长基线干涉测量等。在工业应用领域,雷达、导航、深空探测等方面均需利用超稳微波频率源。目前超高稳定度微波源的实现方式主要有3种:1)传统的通过晶体振荡器多次倍频的方法;2)通过极高Q值的微波腔形成正反馈振荡,并对振荡信号的相位和幅度进行控制,提高其频率稳定度,本实现方式主要指低温蓝宝石微波频率源[7-9];3)将极窄线宽的激光器锁定在高Q值光滤波腔上,然后通过光频梳,得到所需微波信号[10]。其中,采用晶振倍频方式获得的高频段微波源,其稳定度和相噪水平一般[11,18],无法满足部分应用对高性能微波源提出的要求。对于由光频域获得的超稳微波信号,虽然信号的短期频率稳定度能够优于10-15量级,但由于需要依靠复杂的光学系统,连续运行能力差(最长稳定运行时间不超过7d),严重限制了其应用范围。低温蓝宝石微波源采用氦气直接制冷,具有短期频率稳定度高、可靠性高、可长期稳定运行(大于1年)的优势,秒级频率稳定度能够达到3.28×10-15,是不二之选。
自20世纪70年代以来,莫斯科大学[12,13]、美国喷气推进实验室(JPL)[14]、西澳大利亚大学[15]、法国国家科学研究院(CNRS)[16]等研究单位陆续开展低温蓝宝石微波频率源的研究工作。将蓝宝石晶体作为能量储存介质,利用其在低温下具有极低的介质损耗的特点,研制出高Q值蓝宝石微波腔。工作在液氦温度下的X波段蓝宝石微波腔的Q值能够达到109量级。根据Leeson模型,高Q值能够显著降低振荡器的相位噪声水平。经过几十年的发展,目前,国际上低温蓝宝石微波频率源的短期频率稳定度已进入10-16量级[16]。实用化的低温蓝宝石微波频率源已成功应用于甚长基线干涉测量、原子喷泉钟等领域[1-6]。目前,我国尚无相关研究成果,因此,研制的低温蓝宝石微波振荡器,更好的服务国防、科研具有重要意义。本研究团队设计并研制了低温蓝宝石微波频率源,为下一步应用奠定基础。
本文设计并研制了两套工作于回音壁模式的高Q值蓝宝石微波腔,输出频率分别为9.204GHz和9.205GHz,当温度控制在6.4K,且温度波动小于1mK时,Q值分别达到了1.3×108及4.0×108。并根据POUND电路原理研制了稳相电路。在实现频率源起振的基础上,对振荡频率信号的相位进行稳定控制。通过对两套低温蓝宝石微波频率源进行互比,得到频率源秒级频率稳定度为3.28×10-15。
2 高Q值蓝宝石微波腔
高Q值蓝宝石微波腔是整个频率源的核心。它是将圆柱状的蓝宝石晶体固定在铜腔内,通过两个探入铜腔内的耦合环对电磁场进行输入输出耦合,耦合环在铜腔内的高度为蓝宝石介质高度的一半。蓝宝石微波腔结构如图1所示。当蓝宝石微波腔工作在回音壁模式时,电磁波沿着晶体柱面内壁传播,即电磁波在蓝宝石晶体内发生全反射,能量被限制在腔内传播,减小了能量损耗,从而获得较高的Q值。蓝宝石晶体的纯度、腔体设计及加工精度均会影响微波腔的Q值。

图1 蓝宝石腔体结构图Fig.1 Schematic of the sapphire-dielectric resonator
微波腔的具体参数可以通过理论计算或软件仿真确定。使用HFSS高频仿真软件调整蓝宝石晶体及铜腔尺寸,使微波腔工作在回音壁模式下。通过仿真,选定微波腔工作模式为WGH12,0,0模,蓝宝石晶体的直径为51mm,高度为30mm。
蓝宝石晶体在低温下具有低损耗的特点,使得蓝宝石微波腔在低温环境中具有极高的Q值。为维持高Q值,蓝宝石微波腔需连续工作在低温环境中。我们设计并研制了基于液氦的闭循环制冷装置,为蓝宝石微波腔提供低温环境。为保证谐振频率的稳定性,制冷装置需具有极高的温度稳定性和极小的机械振动。作为制冷剂的液氦价格昂贵,而且在制冷装置工作过程中,液氦不断吸收热量汽化,消耗量大。考虑到在应用过程中频率源的维持成本,引入氦气再液化系统,设计了闭循环制冷装置,结构如图2所示。制冷装置工作启动,将氦气输入装置内,氦气再液化系统将氦气液化。液氦经输液管输入至低温杜瓦,对低温杜瓦内的谐振腔进行冷却。吸热后的液氦汽化,氦气返回液化装置进行重新液化,从而实现氦气循环利用。在制冷装置工作过程中,仅需定期补充氦气即可,维持费用低。制冷装置的温度通过控制系统进行控制,工作过程为:低温杜瓦内放置铑铁温度计,温度控制系统采集杜瓦内的实时温度值,经PID控制器处理计算后将加热信号传输给低温杜瓦内的加热装置,从而将微波腔的温度控制在4.2K至15K之间任一设定值上,且温度波动低于1mK。由于机械振动也会对频率源的频率稳定度产生影响,因此,在低温杜瓦外设置减震装置,使机械振动小于1μm。
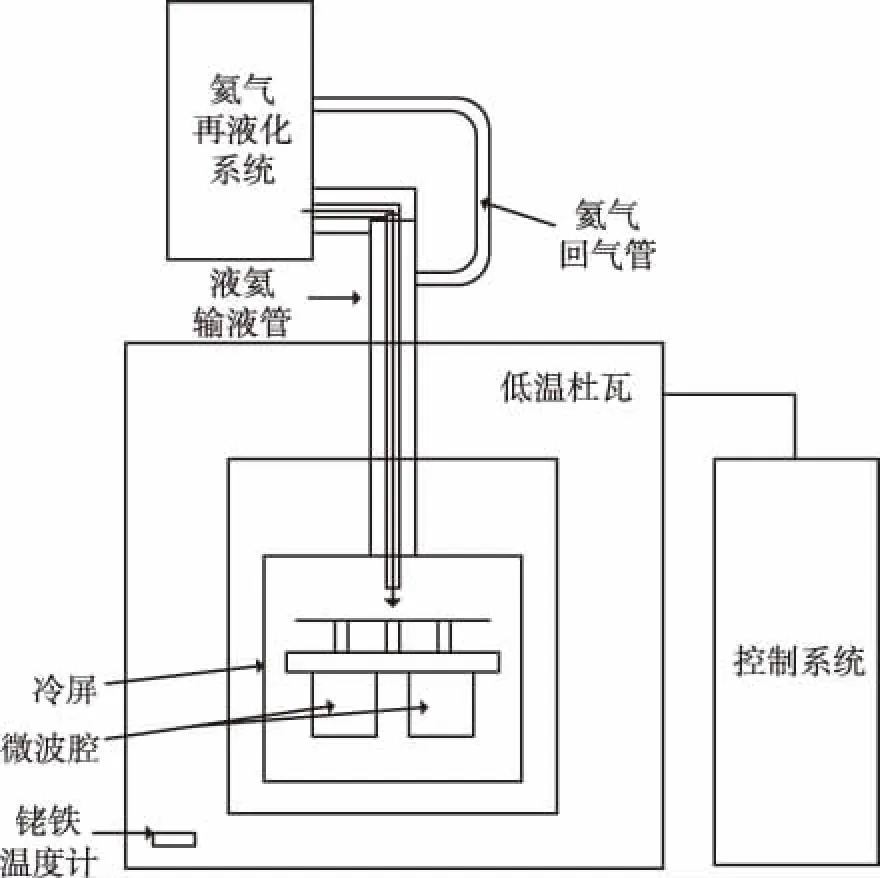
图2 闭循环制冷装置结构示意图Fig.2 Schematic Diagram of the Closed Cycle Cryocooler
由于低温蓝宝石微波频率源的短期频率稳定度较高,目前无法直接测量,为此,我们在低温装置内设计了两套蓝宝石微波腔,通过互比得到相对频率稳定度。
谐振腔内耦合环的大小、探入腔内的深度会影响输入输出耦合系数及Q值,在调试过程中需仔细反复调试以获得最佳输入输出耦合系数及Q值。当低温装置温度控制在6.4K时,实验测得两套微波腔的谐振频率分别为9.204GHz,9.205GHz,如下图所示。经网络分析仪测试,Q值分别为1.3×108及4.0×108。

图3 6.4K温度下谐振频率测试结果曲线图Fig.3 The results of resonance frequency at 6.4 K
3 电路装置
基本振荡环路包括蓝宝石微波腔、低噪声微波功率放大器、移相器、窄带滤波器、环行器、隔离器,如图4所示。其中,蓝宝石微波腔起滤波的作用,配合外加的窄带滤波器,获得在选定的高Q值模式处的振荡信号;由于蓝宝石微波腔及环路中的其它器件、线缆存在一定量的插损,因此,需要低噪声微波功率放大器对振荡信号进行放大,当振荡环路增益与衰减相当时,满足频率源起振的条件之一;由于振荡电路中的器件及线缆均能引入一定的相移,要保证频率源能够起振且振荡信号功率最大,需使用移相器对振荡信号增加额外的相移,并通过调节相移量使得入腔信号的相位与微波腔内信号的相位基本一致。
在基本振荡环路的基础上,为了进一步提高频率源的频率稳定度,采用POUND电路原理,增加相位控制环路,使振荡信号的相位更加稳定,如图4所示。该环路包括检波器、锁相放大器、积分器、压控移相器。通过压控移相器对基本振荡电路中的振荡信号进行频率调制,调制频率由实验确定,我们采用70kHz。检波器将振荡信号转化为包含调制频率信息的电压信号,通过锁相放大器及积分器产生反馈信号,反馈控制压控移相器。
4 频率稳定度测试

图5 频率稳定度测试原理框图Fig.5 The schematic diagram of frequency stability measurement
由于低温蓝宝石微波频率源的短期频率稳定度较高,无法直接测量。研制的2套低温蓝宝石微波频率源,二者共用一套闭循环制冷装置,通过互比得到二者的相对频率稳定度,原理如图5所示。两套频率源输出信号频率分别为9.204GHz和9.205GHz,两个输出信号经混频器,得到频率为209kHz的低频信号。利用时间间隔计数器(Agilent 53132A)测量该低频信号的频率,采样时间1s,并通过GPIB协议传输至计算机进行储存。使用频率稳定度分析软件Stable32计算得到209kHz差频信号的稳定度,结果如图6所示。1s频率稳定度测试结果达到了2.33×10-10。积分时间在(0~2)s范围内时,稳定度与积分时间存在τ-1/2的比例关系,其中,起主要作用的噪声类型是调频白噪声。积分时间约在(4~32)s范围内时,稳定度与积分时间存在τ的比例关系,此时影响频率源性能的主要是频率随机游走噪声,产生这一现象的主要原因是部分幅度噪声能够被转化为频率噪声,我们将在以后的工作中对此进行优化。
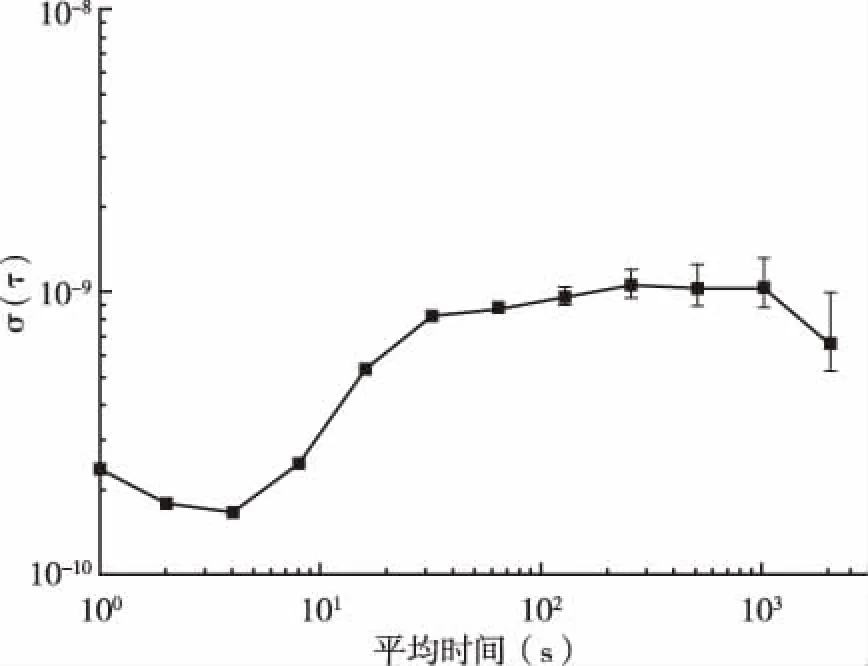
图6 频率稳定度测试结果曲线图Fig.6 The result of frequency stability
由于使用的是Λ型时间间隔计数器,因此计算所得的两个信号的相对方差σΛ(τ)不同于实际的阿伦方差σy(τ)。对于调频白噪声来说,二者存在关系为[17]
σΛ(τ)≈1.14×σy(τ)

5 结束语
本文设计并研制了两套工作于WGH12,0,0本征模式的高Q值蓝宝石微波腔,输出频率分别为9.204GHz和9.205GHz。在基于液氦的闭循环制冷装置为微波腔提供低温环境,该装置具有温度稳定性高、机械振动小的优点。当温度控制在6.4K,且温度波动小于1mK时,微波腔Q值分别达到了1.3×108及4.0×108。在此基础上,根据POUND电路原理研制了稳相电路。在实现频率源起振的基础上,对振荡频率信号的相位进行稳定控制。通过对两套低温蓝宝石微波频率源进行互比,利用时间间隔计数器测量差频信号的频率,并经计算得到频率源秒级频率稳定度为3.28×10-15。

