基于汉默斯里序列抽样的姿控系统随机稳定性评估*

刘晓东 张 玉,2 高 博 杜立夫

1.北京航天自动控制研究所，北京 100854 2.宇航智能控制技术国家级重点实验室，北京 100854

为了克服传统鲁棒控制系统设计方法在工程实际应用中存在的缺陷，在20世纪80年代末、90年代初，美国普林斯顿大学的Stengel等提出了线性时不变控制系统随机鲁棒性的概念[1-3]。通过对控制系统特征值的蒙特卡洛估计获得其随机特征根分布，用标量的不确定性概率来表述随机鲁棒稳定性，并用不稳定概率的置信区间表述蒙特卡洛估计的计算收敛性问题。这种基于随机特征根分布概念的随机鲁棒性分析方法具有较为广泛的适应性，不仅适合于常见的高斯型参数不确定性系统，也适合于非高斯型且有界的参数不确定性系统[4]。

在研究飞行器姿态控制系统的随机鲁棒性能分析时，通常采用蒙特卡洛估计来量化飞行器姿态控制系统的鲁棒性能[5-7]。实际上，飞行器姿态控制系统的随机鲁棒性能分析具体可以分为2个方面：1)控制律设计阶段的随机鲁棒性能分析，目的是采用定量概率形式描述闭环系统统计意义上的稳定性(如判断所有特征根是否都在s平面左半平面)以及稳定裕度(幅值裕度和相位裕度)等；2)控制系统仿真验证阶段的随机鲁棒性能分析，目的是采用定量概率形式评估系统统计意义上的性能指标(如有界稳定性、调节时间、超调量、跟踪精度和约束条件是否被满足等)。

蒙特卡洛抽样(Monte-Carlo sampling，MCS)是一种随机性抽样方法，其关键是产生符合输入状态分布的随机数，其缺点在于计算收敛所需的样本数目多，导致计算量大，计算负担重。为了改善这一问题，提出了利用“充满空间设计”原则的现代试验方法，此类方法能够确保样本点充满整个设计空间，并且最大限度地反映设计空间的特征，进而减小样本数目，提高计算效率。目前常见的“充满空间设计”的抽样方法包括[8]：1)均匀抽样(uniform sampling，US)，一种只考虑样本点在设计空间内均匀散布的抽样方法；2)拉丁超立方抽样(Latin hypercube sampling，LHS)，由McKay于1979年首次提出，采用一种受约束的抽样方法来安排样本点；3)汉默斯里序列抽样(Hammersley sequence sampling，HSS)是以汉默斯里序列点为基础发展出来的一种抽样方法，采用一种低距、超均匀分布的确定性抽样方法来安排样本点。文献[9-11]详细分析了HSS抽样方法相比MCS和LHS抽样方法的优势，其主要体现在多维抽样空间的均匀分布性以及收敛的快速性方面。为了克服传统频域设计中稳定性评估原则的保守性，本文将对飞行器姿态控制系统开展随机稳定性评估研究，并将HSS抽样方法引入其中以代替传统MCS抽样方法，采用定量概率形式描述控制系统统计意义上的幅值裕度和相位裕度，即所谓的控制系统随机稳定裕度评估。

1 问题描述

1.1 传统抽样方法

以二维空间为例，图1(a)～(c)分别展现了MCS、US以及LHS的样本二维分布，抽样数取为100。由此，可以较清晰地展现出3种传统抽样方法在二维空间的样本分布情况。

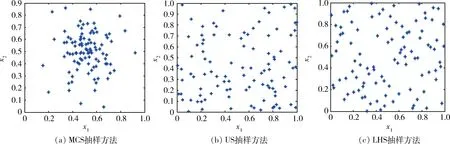
图1 三种抽样方法的样本分布二维图

1.2 基本HSS抽样方法

Hammersley序列生成算法的基本思想是[9]：对于任意一个整数n，若表达为各个位数的组合n=nmnm-1…n2n1n0，则它可以表示为基于一个基数R的形式：

n=n0+n1R+n2R2+…+nmRm

(1)

式中，m=[logRn]=[lnn/lnR]，中括号表示取整数部分。然后，通过颠倒位数的顺序，基于基数R的倒数(称为逆基数)可以在区间[0 1]内构造唯一的小数，该方法可表示为：

φR(n)=n0n1n2…nm=n0R-1+

n1R-2+…+nmR-m-1

(2)

于是，N个k维Hammersley序列点xk(n)可以构造为：

(3)

xk(n)=1-zk(n),n=1,2,…,N

(4)

其中，R1,R2,…,Rk-1表示前k-1个自然素数。基于如上构造方法，选取抽样数目为100，图2展示了采用HSS抽样的样本分布二维图。

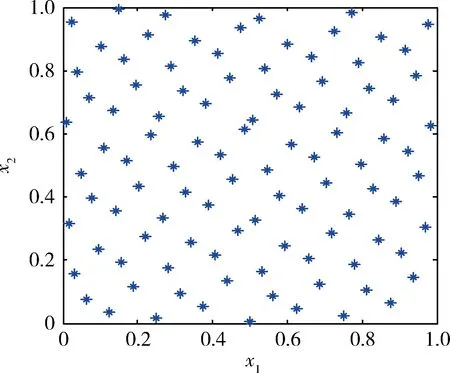
图2 HSS抽样的样本分布二维图

由图1～2可以看出，在指定抽样数目的情况下，US、LHS和HSS抽样3种方法都可以实现样本在整个二维单位空间的分布，然而采用HSS方法时样本分布更加均匀、空间充满特性更好，直观体现出其优势所在。相比之下，MCS样本的局部聚集性较高，若要实现更好的空间填充性，则需要更多的抽样数目。

1.3 归一化HSS抽样方法

因为按照传统汉默斯里序列的生成准则，其生成的样本均匀分布在单位超立方体内，即每一维变量的值均在[0 1]区间内。然而，飞行器各个不确定参数的变化区间并非一定在[0 1]区间内，且不尽相同。因此，在随机鲁棒性能分析之前，需要首先解决多维空间指定区间的汉默斯里序列生成问题，即需要对传统汉默斯里序列的生成准则进行适应性处理。

假设某一维不确定参数的变化区间为[xminxmax]，利用传统汉默斯里序列准则生成的样本值为x(x∈[0 1])，则将x映射到[xminxmax]区间的映射法则如下：

x′=xmin+(xmax-xmin)x

(5)

2 基于HSS抽样的随机稳定性评估方法

频域分析法可根据系统传递函数得到系统相应的频率特性，该频率特性具有较明确的物理意义，并可作为分析控制系统性能的依据。当控制系统阶数较高时，频域分析法避免了直接求解高阶微分方程带来的困难，具有更优越的实用性和方便性，故而在实际设计中得到广泛的应用。在频域设计的指标评估体系中，稳定裕度是衡量闭环系统稳定程度的重要指标，包括幅值裕度和相位裕度。

对于飞行器姿态控制系统的传统设计而言，在系统各种不确定性的极限偏差组合状态下，要求均满足幅值裕度和相位裕度的指标要求，这就给姿态控制系统的设计带来了保守性。因此，将随机鲁棒分析的理念引入到飞行器姿控系统频域设计的稳定裕度评估过程。

下面首先构造随机幅值裕度分析和随机相位裕度分析的概念，定义如下。

随机幅值裕度分析：在系统参数随机变化的情况下，应用统计概率对开环系统可接受的幅值裕度进行描述。

随机相位裕度分析：在系统参数随机变化的情况下，应用统计概率对开环系统可接受的相位裕度进行描述。

考虑随机采样，通过计算样本频率的方法来计算开环系统可接受幅值/相位裕度的概率，即：

(6)

其中，A(v)是开环系统的幅值或相位裕度；v是不确定参数的随机向量；PA是开环系统稳定裕度可接受的概率；Am表示可接受的幅值或相位裕度最小值；M(·)是在N次估计当中幅值或相位裕度可接受的数目。

通过随机幅值裕度和随机相位裕度分析，可以获得开环系统满足设计要求的统计意义上的描述。以此作为设计指标，可以从一定程度上提高设计的灵活性，避免由于传统稳定裕度评估方法带来的保守性。同时，在对系统不确定参数偏差进行随机抽样时，采用归一化的HSS抽样算法进行概率估计，以提高稳定性评估过程的效率。

考虑飞行器姿态控制系统的对象特性和控制器环节，采用基于归一化的HSS抽样算法的随机幅值/相位裕度的概率评估，其概率估计公式如下：

(7)

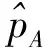
3 仿真结果

本部分将对比采用传统MCS抽样方法以及HSS抽样方法下某飞行器姿态控制系统的稳定性评估情况，并分析本文方法的优势。

选取某飞行特征点用作后续分析，分别采用2种抽样方法对该特征点处的飞行器姿态控制系统进行稳定性评估，而且为了更加清楚地对比2种方法的区别，传统MCS方法的抽样数目选取为20000，而HSS方法的抽样数目仅为10000。下面分别从随机幅值裕度和随机相位裕度2个方面分析统计结果。

首先，图3～4展现了2种抽样方法下飞行器姿控系统相位裕度的统计结果，包括随机分布图、分布直方图、概率分布曲线和概率密度曲线，用于直观了解相位裕度的分布情况。

同样的，由图3～4可以看出：1)两种评估方案下概率统计曲线的大致趋势是相同的；2)当采用本文评估方案时，虽然样本的数目要少一半，但其相位裕度的分布要更广一些，这也从侧面反映出该评估方案的样本分布要更广，即样本的空间充满特性更好。同时，假设可接受的相位裕度至少为30°，那么在HSS抽样方法下可接受相位裕度的概率为M(Pm≥30°)/10000×100%，其中M(Pm≥30°)表示10000次抽样结果中相位裕度大于30°的数目。

图3 采用MCS抽样方案的相位裕度统计结果

图4 采用HSS抽样方案的相位裕度统计结果

然后，对比2种抽样方案下飞行器姿控系统幅值裕度的统计结果，包括随机分布图、分布直方图、概率分布曲线和概率密度曲线，可以得出与相位裕度统计分析时相同的结论。同时，假设可接受的幅值裕度至少为4dB，那么在HSS抽样方法下可接受幅值裕度的概率为M(Am≥4dB)/10000×100%，其中M(Am≥4dB)表示10000次抽样结果中幅值裕度大于4dB的数目。

4 结论

提出了一种基于汉默斯里序列抽样的随机稳定性评估方法，并将其应用于飞行器姿态控制系统的设计过程。相比基于蒙特卡洛抽样的传统评估方法，采用汉默斯里序列抽样的分析与评估方法，不仅可以从一定程度上减小计算机仿真次数，节省仿真评估时间，而且还可以提高收敛精度。计算机仿真结果表明，在采样数目较少的情况下，本文评估方案下样本分布要更广、样本的空间充满特性更好。HSS抽样方法可进一步应用于姿控系统的仿真验证阶段，关于此部分的研究将在后续工作中给出。