固定翼无人机电磁弹射用直线感应电机设计与研究*
刘希军 朱新宇 高丽霞 刘小涵
中国民用航空飞行学院 航空工程学院,四川 广汉 618307
目前,固定翼无人机起飞方式主要有火箭助推起飞、轨道弹射起飞、地面滑跑起飞、空中投放起飞、车载发射起飞、垂直起飞和手抛起飞等。较为常见的方式为火箭助推和气液压弹射技术。火箭助推方式在无人机起飞过程中,释放大量的化学染料、烟尘和火光,成本较高,安全性能较低。气液压弹射技术经济适用性较好,但其结构管路复杂,占地面积大,设备维护复杂性高[1]。
随着电磁加速技术研究的不断提升,越来越多的研究倾向于采用电磁弹射驱动固定翼无人机加速起飞。电磁弹射驱动效率高,精度高,加速均匀,维护方便[2]。相较于其他助推驱动而言,电磁驱动装置不存在无效载荷,动力源成本低,耗能更少,噪音更小,且不会对环境造成污染。
针对无人机电磁弹射研究主要有线圈弹射和直线电机2种方式,相较而言,采用直线感应电机作为电磁驱动装置,可通过改变设计参量改变电磁推力输出,推力输出更大更平稳,精度高,可控性强,设备更易于维护。通过对无人机起飞运动学分析,优化设计无人机起飞用长初级直线电机,验证固定翼无人机弹射起飞的可行性。
1 无人机起飞运动学分析
采用电磁加速系统在预定的长度距离内,将固定翼无人机瞬间加速,并使其速度值达到无人机起飞规定标准。无人机发射简化受力模型如图1所示。
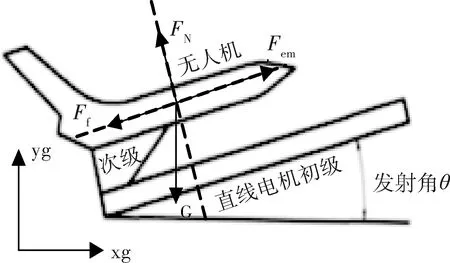
图1 无人机发射简化受力模型
假定被加速的轻型固定翼无人机及其载荷质量不超过40kg,弹射轨道长度5m,无人机要在0.36s内从0km/h加速到100km/h,加速过程中无人机自身动力系统不做功,直线感应电机提供恒定的电磁推力输出,用于无人机的加速起飞牵引动力。
由牛顿第二定律对运动学过程表示为
(1)
(2)
(3)
式中,vt、Ls和t分别为固定翼无人机加速末速度、轨道长度以及加速时间;F、M和a分别为无人机沿轨道方向受到合力、无人机及动子滑块总质量以及无人机的加速度。
其中,无人机沿轨道弹射方向合力为
F=Fem-(Ff+Gsin(θ))
(4)
Fem为直线电机产生的电磁推力;Ff为无人机弹射过程中受到的阻力;G为无人机及动子滑块总重量;θ为发射角度,发射角度小于60°可调。
固定翼无人机在起飞弹射加速过程中,由于前部空气被压缩,机身两侧面空气摩擦,以及尾部空间部分真空等因素,导致加速了过程空气阻力。
无人机所受空气阻力大小与其速度平方成正比,速度越大,所受空气阻力越大。无人机所受空气阻力为:
(5)
式中,C为阻力系数,其值的大小主要和运动物体的形状、光滑程度以及迎风面物体的面积有关,无人机的风阻系数约为0.2~0.4;ρ为空气密度,干燥空气密度为1.293g/l;S0为物体迎风面的面积;v为物体与空气的相对运动速度。
以固定翼无人机及其载荷质量40kg、发射角30°计算,所受空气阻力相对于电磁推力较小,暂且忽略,欲使无人机在5m内加速到100km/h,则直线感应电机至少提供3.09kN的电磁推力。固定翼无人机加速过程具体指标如表1所示。
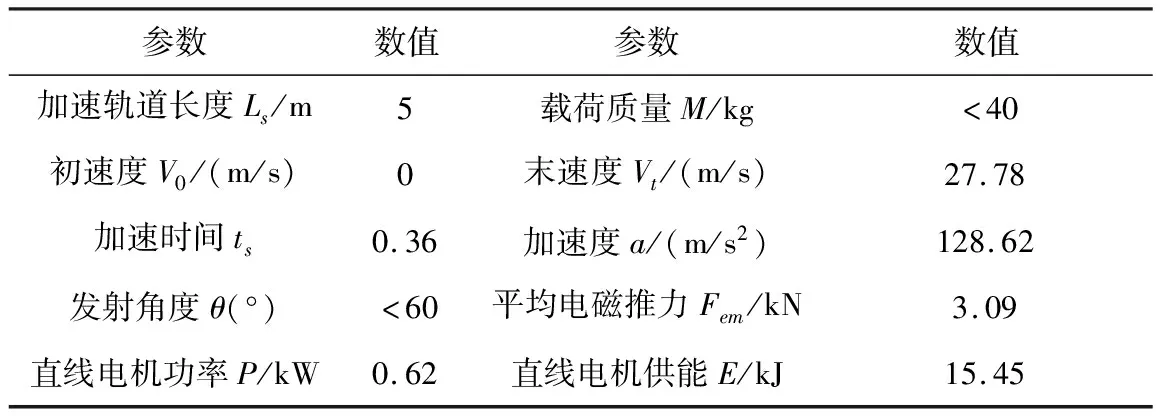
表1 无人机加速主要技术指标
2 直线感应电机数学模型建立
固定翼无人机起飞驱动用直线电机采用长初级无槽直线感应电机,其结构图如图2所示。电机的定子采用无齿槽的结构,这种方式可以增大定子绕组截面积,并减小磁场的齿谐波影响[3]。次级为铝板或铜板,减小质量,降低制造和运行成本,且有利于进行高速大推力运动。
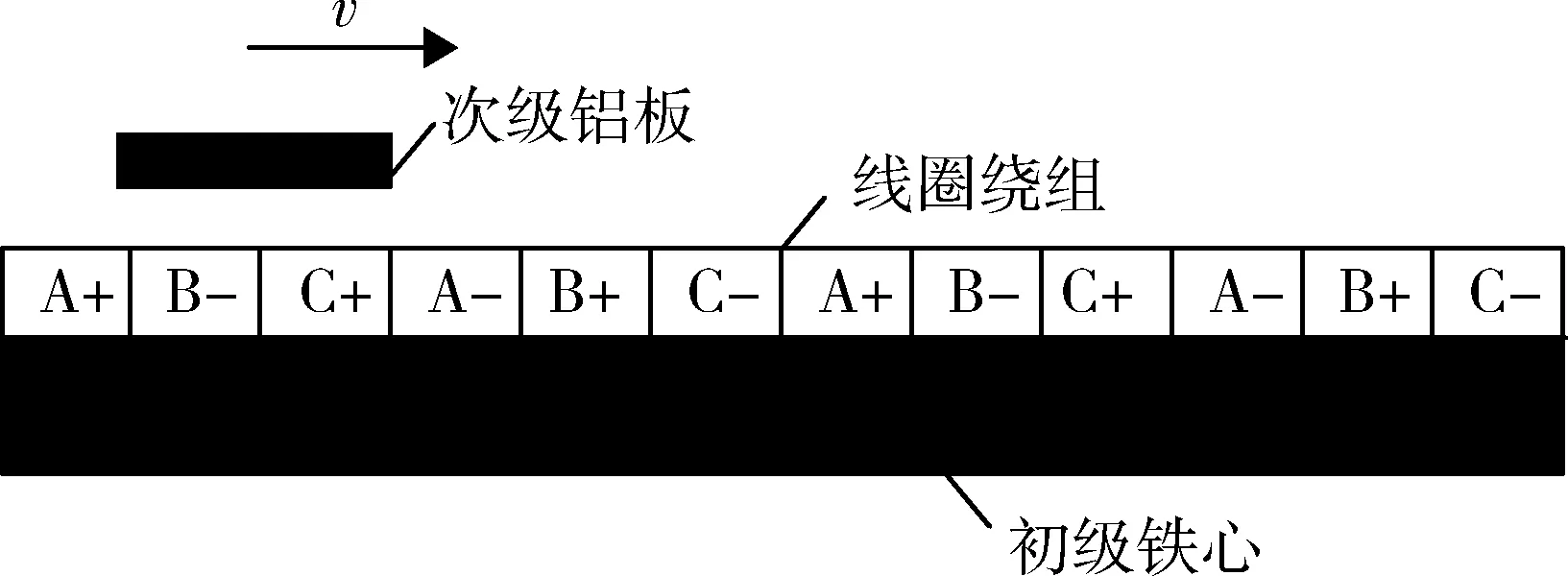
图2 无槽直线感应电机结构图
由于直线感应电机初级铁心及绕组两端开断,这种特殊结构使得直线电机中存在边端效应问题,影响气隙磁场,衰减推力输出,边端效应对电磁推力的输出影响不可忽略。在无人机加速过程中,可采用控制直线感应电机的定子的电流及滑差频率,从而完成电机电磁推力输出的优化控制。
考虑边端效应对长初级无槽直线感应电机的影响,建立直线感应电机T型等效电路,推导电机电磁推力输出表达式,通过等效电路可以计算出直线感应电动机相关的机械特性。考虑边端效应的长初级直线感应电动机的等效电路如图3所示。

图3 考虑边端效应的直线电机等效电路图

(6)
式中:
(7)
ρa为次级电阻率;la为次级导体宽度;ω1为初级相串联匝数;p为直线电机极对数;da为次级导体厚度;τ为直线电机极距。当电机结构参数确定后,边端效应等效电阻Red仅与滑差率s相关。
3 直线感应电机推力分析
采用基尔霍夫定律计算分析考虑边端效应的无槽单边直线感应电机等效电路。由基尔霍夫电压定律可得:
(8)
(9)
(10)
由基尔霍夫电流定律可得:
(11)
根据考虑端部效应的直线感应电机等值电路和基尔霍夫定律,推导无人机起飞驱动用直线电机电磁推力输出:
(12)

(13)
整理式(12)和(13)可得电磁推力输出:
(14)
额定频率f1,滑差频率fs与滑差率s存在关系:
fs=s·f1
(15)
因而可通过控制滑差频率,改变所需电机的动力输出。
在驱动过程中,通过控制滑差频率控制直线感应电机的电磁推力输出,即保持电机初级绕组电流值恒定不变,亦可通过控制滑差频率控制气隙磁场及涡流场,进而实现电磁推力输出的控制。
根据无人机加速运动学性能指标要求,设计弹射用直线感应电机尺寸,进而确定等效电路各参数值。
(16)
式中,kr1为电阻增长系数,取kr1=1;ρ为绕组导线电阻率;lav为初级绕组平均半匝长度;S1为初级绕组导线截面积。
忽略气隙基波漏电抗,则初级绕组漏电抗x1为:
(17)
式中,lδ为电机初级铁心叠厚;q1为电机每极每相槽数。
(18)
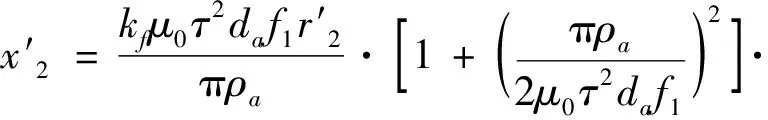
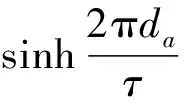
(19)
kdp为基波绕组系数[4-5],kdp=1;da为次级铝板厚度;kf为集肤效应系数[6],忽略集肤效应,则kf=1。
励磁电抗x0为:
(20)
式中,μ0=4π×10-7H/m为真空磁导率;δe为电磁气隙。
4 直线电机参数设计及分析
根据固定翼无人机加速起飞设计指标要求,设计一款加速驱动用无槽型单边直线电机,用于提供无人机在起飞阶段的电磁推力输出。设计加速驱动电机部分尺寸参量如表2所示。
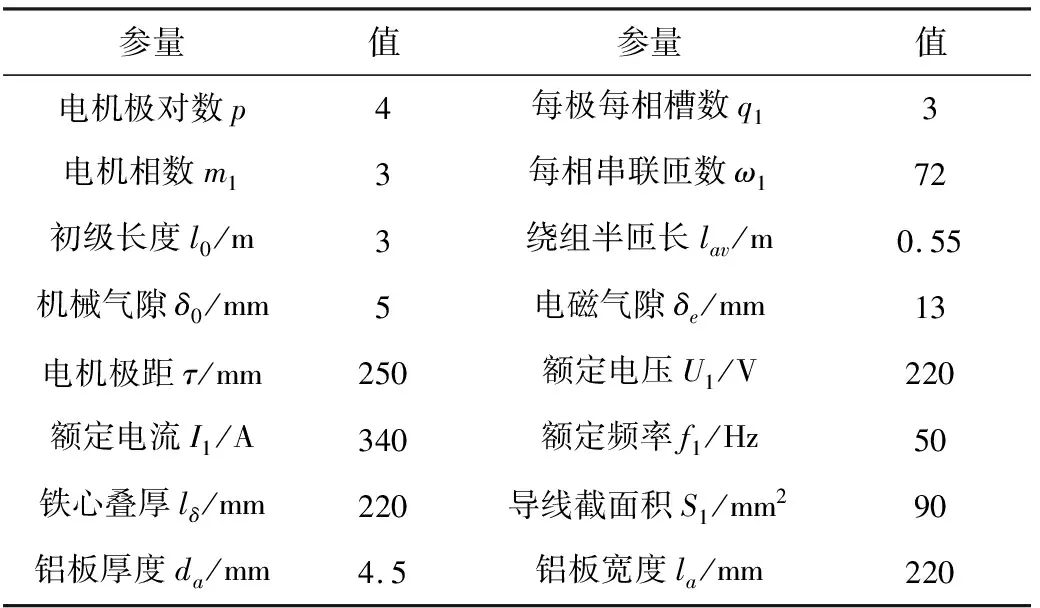
表2 无槽单边直线感应电机设计部分参量
电机极距的变化将影响电机电磁推力的输出。增大极距有利于增大基本行波推力,但极距的增大会造成端部漏抗和损耗的增加。同样,直线电机极距不易过小,过小的极距不利于电磁推力的输出,又会增大气隙磁场基波漏抗。通常,加速用长初级直线感应电机极距的取值范围为τ=0.2~0.5m。
适当增加电机极数有利于减小端部极所占总比重,进而减小纵向端部效应的影响。然而,当直线电机的长度和极距确定后,电机的极数必然受到制约。通常,直线电机极数取值为p=4~8。
传统型直线电机均采用齿槽结构,对于大功率电磁加速用长初级直线感应电机,无齿槽的设计方式,有利于增大定子绕组截面积,亦可以有效的消除气隙磁场齿谐波[7-9],每极每相槽数取值为q1=1。
电磁加速用大功率直线感应电机常采用单条式绕组,每相串联的匝数与供电线电压成正比,和供电频率成反比。调整每相串联匝数可以保证直线电机输出被加速物体所需的电磁推力的输出。
初级铁心宽度的选取通常和直线感应电机的极距τ相关联,初级铁心宽度的取值范围为la0=(1.5~3.5)τ。
为了减小横向端部效应,直线电机次级宽度应略宽于初级铁心宽度,横向每边伸出长度应大于τ/π,因而,次级导体的宽度选择为la=la0+2τ/π。
根据直线电机次级导体板所承受的剪切应力和导体板宽度,确定次级导体的长度值[10]。
直线电机次级导体板的厚度选取同样与电磁推力相关。厚度太小会减小行波推力输出,而厚度过大时,端部效应越发明显。加速用直线感应电机的次级板导体厚度通常选取为da=3~5mm。
悬浮气隙值对直线感应电机电磁推力输出影响明显。无人机加速系统用直线电机的机械气隙为5mm,电磁气隙13mm,分析无人机运动速度20m/s时,电磁气隙和直线电机推力的关系如图4所示。
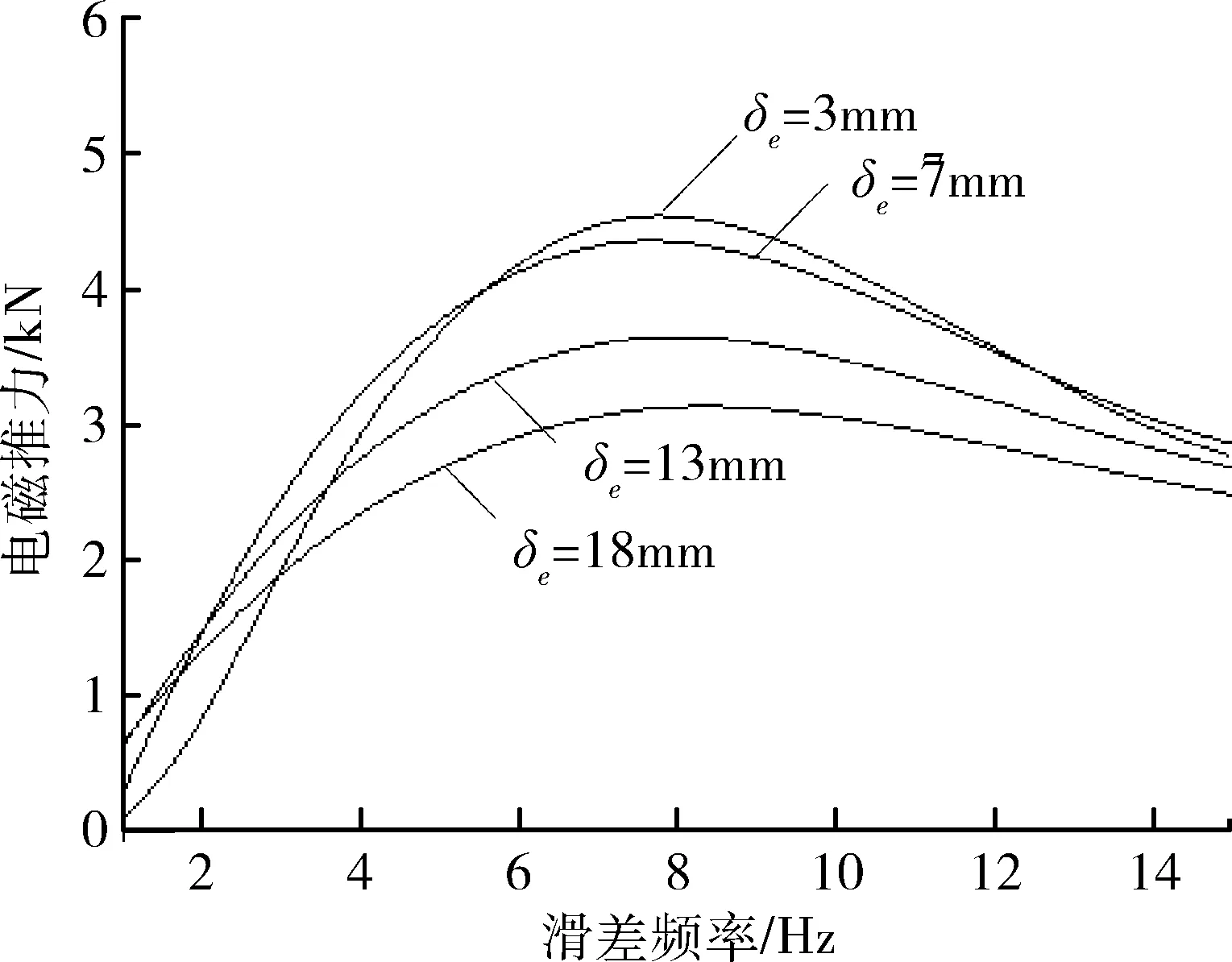
图4 不同电磁气隙下滑差频率与电磁推力关系
通常,设计直线电机时应尽量减小气隙长度,气隙长度的大小与电磁推力输出成反比。如图所示,这种关系在滑差频率大于7Hz时尤为明显。
由于受到实际加工工艺的限制,以及热膨胀的制约,电机气隙长度不宜过小,气隙长度过小会增加空间谐波磁场产生的附加损耗和脉振推力。
当滑差频率大于14Hz时,不同气隙下的推力输出值趋于恒定且近似相近。
5 直线感应电机控制分析
固定翼无人机加速驱动用直线感应电机参数设计完毕后,对直线电机的控制方式进行仿真验证。建立直线感应电机模型,仿真验证理论分析计算的有效性。不同滑差频率下,无人机加速过程中,运行速度与电磁推力输出关系如图5所示。
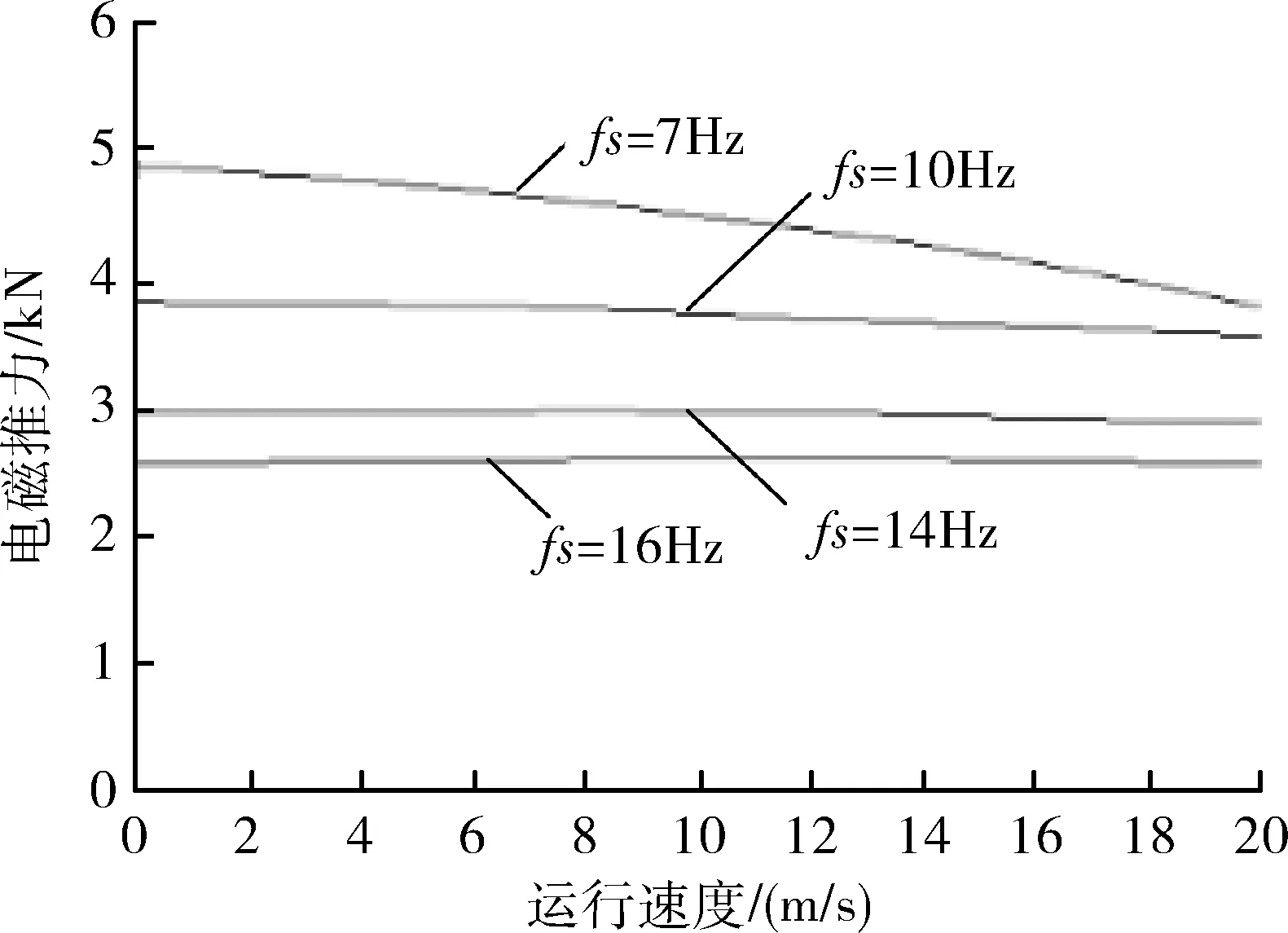
图5 不同滑差频率下运行速度与电磁推力关系
固定翼无人机起飞加速过程中,选取的滑差频率越小,对应的电磁推力输出越大。保持滑差频率恒定,驱动用直线感应电机电磁力输出随无人机运行速度的增大基本保持不变,且滑差频率取值14Hz左右时,电磁力输出值受速度影响最小。
不同运行速度下,固定翼无人机加速过程中,滑差频率和直线电机推力的输出关系如图6所示。

图6 不同运行速度下滑差频率与电磁推力关系
滑差频率较低,速度不同,对应的电磁推力输出亦不相同;滑差频率较高,电磁推力输出基本不随速度的改变而改变。通过调节滑差频率可以实现更大的电磁推力输出,但同时过高的滑差频率会增大驱动系统的功能损耗。磁悬浮列车用直线感应电机,滑差频率取值13.69Hz时[11],系统功耗最低。本加速系统采用滑差频率取值14Hz完成固定翼无人机的加速弹射。
6 结论
随着对固定翼无人机起飞加速要求的不断提高,传统型的起飞方式已经逐渐无法满足无人机的起飞加速需求。本文研究了一种利用无槽式长初级直线感应电机作为驱动的电磁弹射加速方式。分析了无人机加速起飞的运动学过程,并根据起飞要求计算直线电机所需的电磁推力值,并以此为基础设计一款用于加速系统用的直线感应电机,完成无人机的加速起飞。
直线感应电机的控制方式采用恒电流-滑差频率控制,仿真分析不同滑差频率对电磁推力输出的影响,优化系统控制方式,减小驱动系统的功耗,完成固定翼无人机起飞需求。

