基于相平面控制的固体火箭快速精确入轨策略

吴 楠 张 力

1.战略支援部队信息工程大学，郑州 450001 2.西安卫星测控中心着陆场站，渭南 714000

随着空间技术的不断发展，其军事应用正从空间支援向空间作战转变[1]，某些特殊任务要求载荷要以同时满足终端位置和速度矢量(即六轨道根数)约束条件下直接入轨，做到“快速精确进入空间”。固体小型运载火箭是实现这一要求的有效途径，但对入轨弹道规划提出了新的要求。

固体小型运载火箭的入轨弹道规划，一般有以下2种方法：a)以满足入轨点约束、燃料最省为性能指标，基于弹道计算模型，采用数值优化算法对飞行程序参数进行寻优，进而获得最优入轨弹道[2-4]；b)在原始弹道的基础上，入轨段弹道采用迭代制导方法，控制火箭以满足终端约束入轨[5-7]。以上2种方法均对某种性能指标(通常为燃料最省)具有最优性，但无法达到以满足六轨道根数约束快速进入空间的要求：对于前者，任务的不确定性导致入轨条件不断变化，较长的规划迭代时间影响了方法的快速响应性，且六轨道根数约束过强(通常为3到5个)，全局最优解不一定存在；而对于后者，只能控制推力方向无法改变推力大小的推力模式决定了该方法无法对入轨点x方向位置分量进行控制，即无法以满足六轨道根数约束精确入轨。

本文提出了一种基于相平面控制的入轨弹道设计策略，假设运载火箭采用四级固体发动机，其中前面三级采用固定飞行程序[8]，四级飞行段作为入轨段，基于相平面原理提出并证明在入轨段经过2次恒定方向推力可使火箭以满足位置和速度矢量约束直接入轨，并给出火箭入轨段初始点与入轨点状态所需满足的条件。进而推导了初始点及入轨点状态与推力方向角的关系方程组，采用数值方法求解该方程组获得弹道设计需要的推力方向角。

1 2次恒定加速度的相平面控制策略

仅考虑火箭的质心运动，不考虑绕心运动，即可以把火箭简化为一质点，通过改变过质心的火箭发动机推力方向对该质点的运动进行控制，控制量为推力方向角(俯仰和偏航)。

对于该种情况，火箭入轨段的相平面控制策略为：假设入轨段飞行时间已知，将入轨点状态反向轨道积分至入轨段飞行初始时刻，得到一个“虚目标”的初始位置速度状态，基于相平面的bang-bang控制原理对火箭与虚目标间的相对运动进行控制，经过2次恒定方向推力使得当入轨段飞行结束时，火箭与虚目标相对运动相平面的相点运动到坐标原点，即相对位置速度均为0，此时火箭自然以满足终端位置和速度矢量约束入轨。

为了便于阐述2次恒定方向推力的相平面控制入轨策略，首先引入以下简化假设：a)引力加速度为常值；b)质量恒定，恒定推力即为恒定加速度；c)火箭在发射惯性系的xoy平面内运动，决定推力方向的姿态角仅为俯仰角φ。

“虚目标”其实就是在目标轨道上运行的虚拟载荷，只受地球引力作用，且经过入轨段飞行时间T后，“虚目标”与入轨点状态保持一致。因此若已知入轨点的状态XTf(位置、速度)，可反向轨道积分获得虚目标在火箭入轨段飞行开始时刻的状态XT0，与火箭开始时刻的状态XM0相减，得到火箭与虚目标的相对状态X0=XM0-XT0。相应的相对动力学方程为

(1)

式中:r表示发射惯性坐标系下火箭与虚目标的相对位置矢量;aM和aT分别表示该坐标系下的火箭加速度矢量和虚目标加速度矢量。由于虚目标无推力，且火箭与虚目标的距离较近，可认为二者引力加速度相等，根据假设xoy平面内相对动力学方程的标量形式为

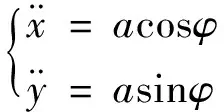
(2)

式中:a表示常值火箭推力加速度。

当火箭姿态角恒定时，根据式(2)可分别得到相对运动x和y轴过相平面原点的相轨迹方程

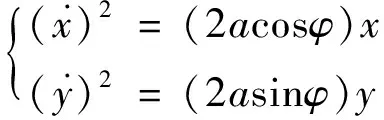
(3)

式(3)表明φ值的不同取值使得过原点的相轨迹为一簇抛物线，φ值决定了抛物线开口的大小。

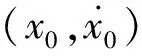
(4)

必存在一个φ值

(5)

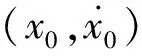
(6)

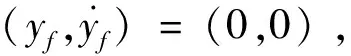
(7)

以上推导说明对于无法改变推力大小、只能改变推力方向的火箭入轨飞行段，利用传统bang-bang控制(一次恒定方向推力)只能对某一坐标轴的位置和速度进行控制，入轨点约束无法全部满足。

为了解决这个问题，对传统相平面法的控制方式进行扩展，在整个入轨飞行段，进行2次恒定姿态角的常加速度控制，控制时间分别为T1和T2，二者满足T1+T2=T，相应的俯仰角分别为φ1和φ2，是可以调整的参数。当x轴和y轴相平面的初始相点满足一定条件时，通过对参数(T1、φ1和φ2)的调整，可使2个相平面的相点同时到达原点。下面给出x轴和y轴相平面的初始相点所需满足的条件。

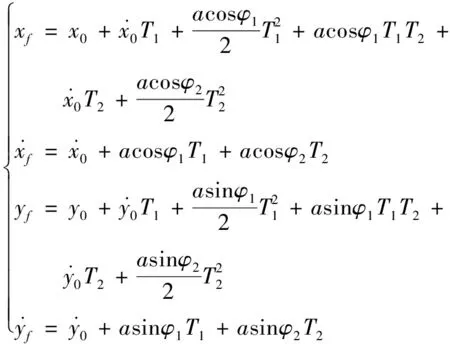
(8)

(9)

将式(9)等式两侧分别平方，位置和速度项分别相加可得

(10)

(11)

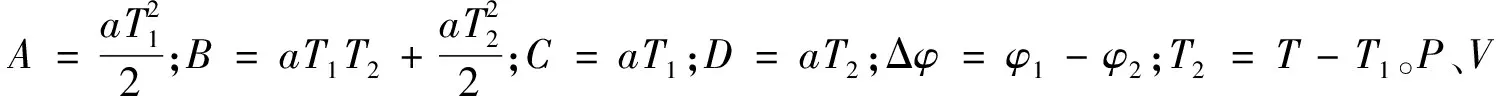
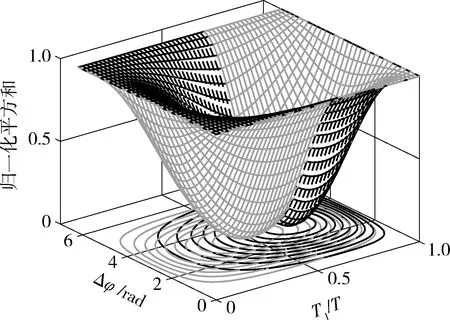
图1 P、V随Δφ和T1变化的曲面

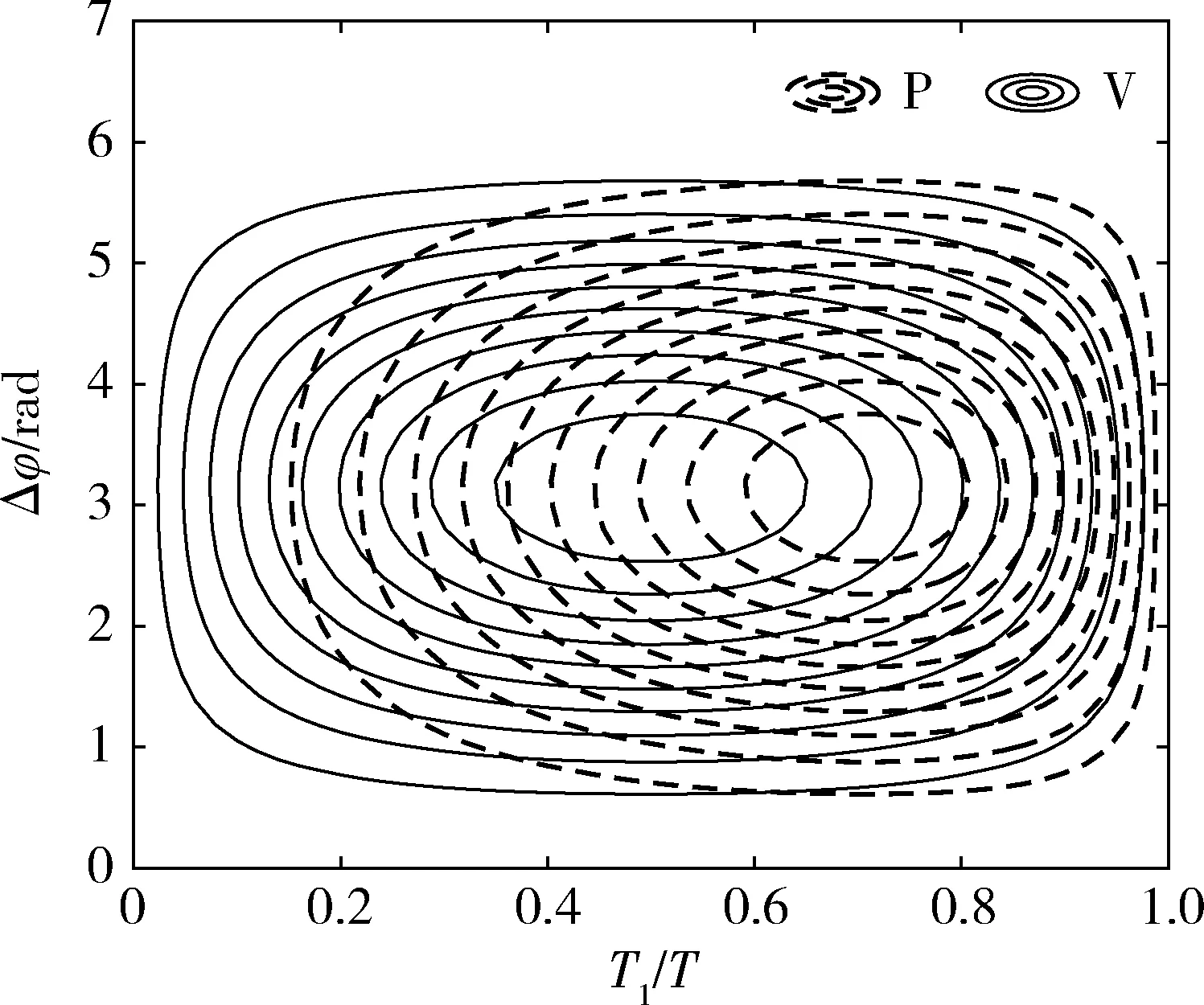
图2 P、V的等值线

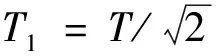
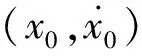
(12)

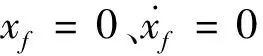
由上述两个条件所确定的y轴相平面初始相点取值范围与式(7)相比有了很大的扩展，x轴和y轴相平面的初始相点选取具有一定的自由性，因此2次恒定姿态角的常加速度控制方法具有实用性。对满足条件的x轴和y轴相平面的初始相点，利用该方法通过对参数(T1、φ1和φ2)的选择，可使2个相平面的相点同时到达原点，即相对位置速度均为0，保证火箭入轨时终端位置和速度矢量约束同时满足。

2 三维空间变质量条件下的姿态角解算

在固体火箭入轨飞行段，火箭在三维空间运动，姿态角不仅包括俯仰角φ，还有偏航角ψ，且火箭的质量是变化的，若假设质量变化率恒定，则加速度按双曲线规律变化。将2次恒定加速度的相平面控制方法用于火箭入轨飞行段弹道设计，需对方法进一步扩展：a)2段的姿态角控制参数为(φ1、ψ1)，(φ2、ψ2)；b)为便于公式推导与分析，根据视速度与时间的一一对应关系，采用视速度模量耗费量[9]W1和W2代替时间T1和T2作为控制变量。

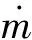
(13)

假设初始时刻视速度模量耗费量W0=0，2次恒定姿态角推力控制结束时的视速度模量耗费量分别为W1和W2

(14)

式中：m0为火箭初始时刻质量。当入轨段飞行时间T固定时，W1和W2不独立，两者的和为定值

(15)

经过2次恒定姿态角的推力控制后，x轴方向的相对位置速度与(W1,φ1,φ2,ψ1,ψ2)的关系为

(16)

(17)

同理可得y和z轴初始相对状态与控制参数的关系

(18)

式中

(19)

与第1节类似，当初始相对位置速度满足式(20)，且PI和VI值较为接近时，则存在方程组(17)和式(18)的一组解(W1,φ1,φ2,ψ1,ψ2)，可使3个坐标轴相平面的相点同时到达原点，在三维空间中保证火箭入轨段飞行结束时终端位置和速度6个分量的约束同时满足。

(20)

方程组(17)和式(18)无法直接求解，建立无量纲化指标函数

J=((x0-Cx)/Re)2+((y0-Cy)/Re)2+

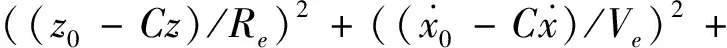
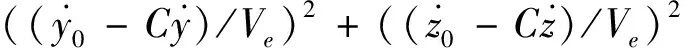
(21)

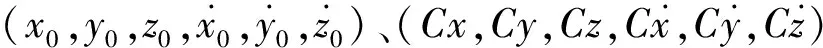
采用数值方法寻优的关键是给出合理的设计变量初值，假设2次推力方向均与待增速度矢量相同，则初值可用式(22)计算

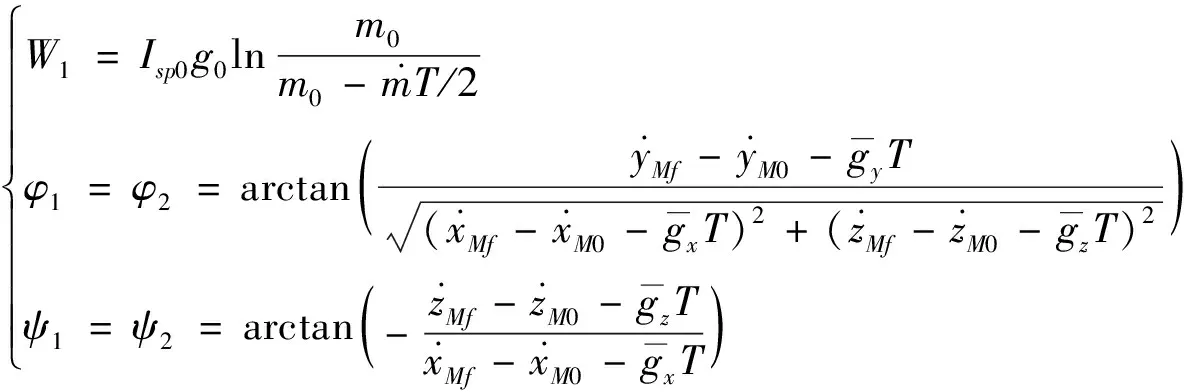
(22)

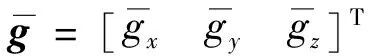
当获得火箭入轨飞行段初始状态XM0、入轨点状态XTf和飞行时间T后，利用本节算法进行推力姿态角解算的流程为：

(a)将入轨点状态反向轨道积分至入轨段飞行初始时刻，得到虚目标的初始状态XT0；

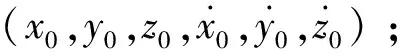
(c)利用式(20)计算PI和VI值，如果满足式(20)，说明解存在，转入下一步；如果不满足，说明需要消除的相对偏差量大于火箭拥有的视速度模量耗费量，即相对偏差过大已超出了火箭的修偏能力，方程无解，此时应重新设计初始点或入轨点，以减小相对偏差，或增加视速度模量耗费量，以增大火箭修偏能力，改变幅度至PI和VI值满足式(20)止；

(d)若解存在则利用式(22)求出设计参数(W1,φ1,φ2,ψ1,ψ2)的初值；

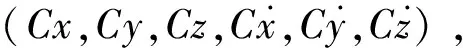
3 仿真验证

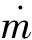
根据初始相对状态计算PI=0.9854，VI=0.9719，可知解存在，然后利用式(22)求出设计参数的初值如表2，采用数值方法进行参数寻优，获得最优的设计参数值(见表2)，相应的指标函数极小值为Jmin=1.135×10-10，可知此时对应的设计参数即为方程组的解。

将优化的设计参数代入火箭入轨飞行段的弹道计算，得到火箭的实际入轨点状态和入轨点偏差如表1，可知精度满足入轨要求。图3～5给出相对运动3个坐标轴方向的相轨迹曲线，可以看出每个方向的相轨迹均由2段曲线拼接组成，相点经过2次转移最终同时到达原点，火箭的终端位置速度约束同时得到满足。

表1 仿真算例中各状态参数

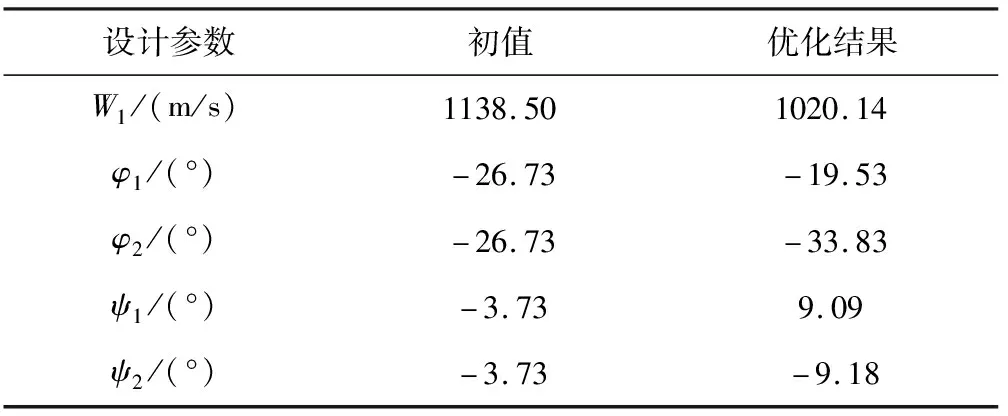
表2 设计参数的初值和优化值

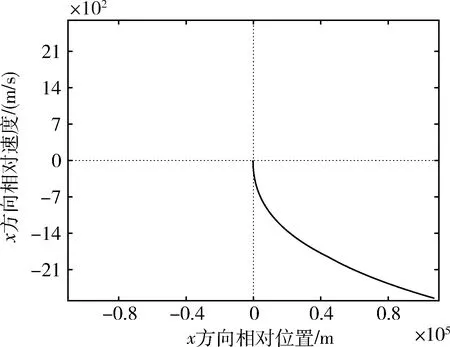
图3 x方向相对运动的相轨迹

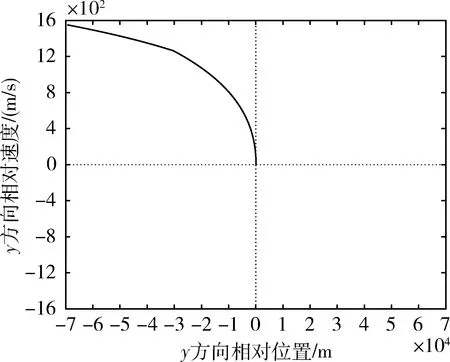
图4 y方向相对运动的相轨迹

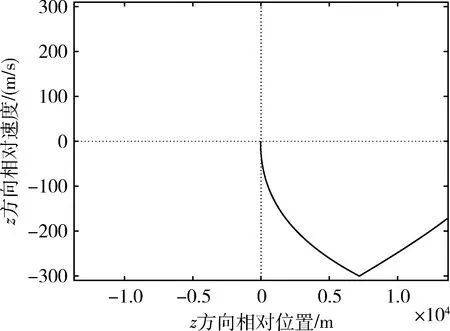
图5 z方向相对运动的相轨迹

对于本文算例，采用迭代制导方法进行入轨计算，与本文算法进行比较分析。制导结束时火箭状态参数以及入轨偏差结果如表1所示，整个制导时间为69.12s，推力方向角俯仰角由-24.6(°)近似线性变化至-47.5(°)，偏航角由2.6(°)近似线性变化至-9.6(°)。对比二者结果可知：迭代制导方法的位置误差要显著大于本文算法，尤其是x方向位置误差较为明显，但迭代制导方法所需时间较本文算法少0.88s，即燃料可节省10.2kg，且迭代制导方法的推力方向角为连续变化，更易进行控制。

4 结论

1)对于无法改变推力大小、只能控制推力方向且飞行时间固定的火箭入轨飞行段，证明了经过2次恒定方向推力使火箭以同时满足位置和速度矢量(即6轨道根数)约束直接入轨的可行性，并推导出火箭初始状态与入轨点状态所需满足的条件；

2)为保证火箭以满足6个轨道根数约束直接入轨，提出一种基于相平面控制原理的入轨段弹道设计方法，通过2次恒定方向推力控制使火箭在入轨段飞行结束时直接入轨，入轨精度满足要求；

3)推导了火箭初始状态、入轨点状态与控制参数(视速度模量耗费量和推力方向角)的关系方程组，采用参数寻优的数值方法对方程组进行求解以获得弹道计算所需的控制参数。由于本文算法明确定义了控制方式，使解的范围大大缩小，且获得了输入变量与输出变量间的解析表达式，因此与传统轨迹优化方法相比，本文算法在控制参数的解算上更为简便和稳健，极大地缩短了弹道设计的耗时；

4)本文算法是以放弃燃料最省的最优性换取对6个要素的控制，且对满足一定条件的初始状态才有解，因此与迭代制导方法的结论并不违背。本文算法兼有能量管理[11]的目的，保证火箭入轨的同时发动机消耗掉多余燃料，实行耗尽关机，简化了入轨级发动机的设计。